Design of Smith Predictor Based Fractional Controller for Higher Order Time Delay Process

P.R.Hemavathy ,Y.Mohamed Shuaiband S.K.Lakshmanaprabu

Abstract: Normally all real world process in a process industry will have time delay.For those processes with time delays,obtaining satisfactory closed loop performances becomes very difficult.In this work,three interacting cylindrical tank process is considered for study and the objective of the work is to compensate for time delays using smith predictor structure and to maintain the level in the third tank.Input/Output data is generated for the three interacting tank process.It is approximated as Integer First Order Plus Dead Time system(IFOPDT)and Fractional First Order Plus Dead Time system(FFOPDT).Smith predictor based fractional order Proportional Integral controller and Integer order Proportional Integral controller is designed for the IFOPDT and FFOPDT model using frequency response technique and their closed loop performance indices are compared and tabulated.The servo and regulatory responses are simulated using Matlab/Simulink.

Keywords: Fractional order proportional integral controller,frequency response technique,smith predictor,three interacting tank process.

1 Introduction

All the industrial process will have significant dead time.Drawback of PI/PID controllers and advanced control techniques is that it will not consider time delay.In those cases,the closed loop system performance can be improved by dead time compensator such as using predictor structure[Smith(1959)].Although the Smith predictor provides improvement,the closed loop performance will be poor.Many approaches have been suggested to overcome those limitations in order to improve the performance of the Smith predictor control system by determining and tuning the parameters of an appropriate controller[Astrom,Hang,Lim et al.(1994);Hagglund(1992);Lee,Lee,Sung et al.(1999);Morari and Zaffiriou(1989);Zhou,Wang,Min et al.(2007)].

Analytical method of designing controllers for time delay systems are proposed[Rao and Chidambaram(2007)].Some of the frequency response based techniques have been reported by researchers[Ho,Hang,Cao et al.(1995);Fung,Wang,Lee et al.(1998);Pegel and Engell(2000);Nagrath and Gopal(2008)].But still these methods are complicated and require a good knowledge in frequency domain.In recent years,the fractional calculus study and its applications towards control theory has been increased rapidly.Podlubny[Podlubny(1999)]suggested a generalized fractional PID controller,PIλDµ,in which λ represents fractional-order integrator and μ represents fractional-order differentiator.Due to increase in parameter,this type of controller provides more flexibility in the controller design.However,the tuning rules applied for fractional-order controllers are more difficult than conventional PI/PID controllers.Several design techniques for designing fractional controllers have been introduced in the literature[Monje,Vinagre,Feliu et al.(2008);Monje,Chen,Vinagre et al.(2010);Padula and Visioli(2011)].Fractional order controller design for time delay process using frequency domain technique has been reported by researchers[Vu and Lee(2013);Vu and Lee(2014)].In this work,real time three interacting tank process is considered.Smith predictor based FOPI controller is designed for the reduced integer order FOPDT system and fractional order FOPDT system using frequency domain technique in order to maintain the level of the tank 3,i.e.,h3and also to compensate for time delay.The paper is structured as follows:Section 2 discusses the three interacting tank process description and data driven modeling.The input output characteristics are discussed in the Section 3.The smith predictor design procedure is explained in Section 4.The controller design applied for three interacting tank process has been discussed in detail in Section 5 and section 6 gives the conclusion of the proposed work.

2 Process description

The three interacting tank process is the benchmark process for the higher order system,where the system contains one manipulated control inputs and three water level outputs.The aim of this work is to develop a control system to control the water level of the third tank by manipulating the voltage applied to pumps.The three interacting tank process is non-linear.The control problem is complicated due to the nonlinearity of the system.

The control of level in a three interacting tank process is quite complicated because of its interaction between the three tanks that is,the response of each tank depends on the response of other tanks,and hence requires complex design and implementation procedure.The water from the reservoir is pumped to tank 1 by the pump and it offers some delay to reach the tank from the reservoir.The output of tank1 is the input for tank 2 and output of tank 2 is input for tank 3.The liquid level of all the tanks are measured using differential pressure transmitter and it is connected to personal computer using data acquisition board.The experimental setup of the three interacting tank process is shown in Fig.1.

Figure 1:Experimental set-up of the process

Table 1:Three interacting tank process parameters

3 Empirical modeling

The three interacting tank process input and output data are generated by applying step variation in the manipulated input.The steady state values for outputs are measured and then input and output characteristics of the system is plotted to understand the dynamic behavior of the system.The values input and output at steady state is tabulated in Tab.2.Fig.2 shows the I/O characteristics plotted for the three interacting tanks for varying values of the manipulated variable,u1.In the present work,the inflow u1alone is considered as input and the inflow u2is not considered that is,it is left to zero and the height of the third tank h3is considered as the output of the process.

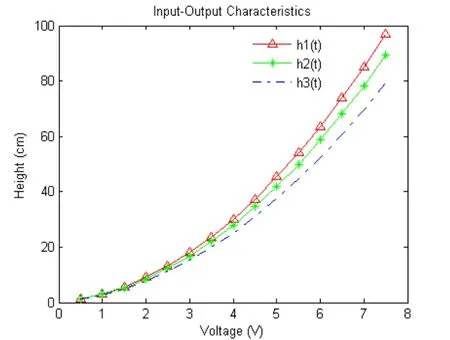
Figure 2:Input/Output characteristics of the process for varying values of u1

Table 2:Steady state values obtained from the experimental setup

The third order transfer function obtained for the process is given by

The time delay in the above transfer function implies the time taken for the water to reach the tank from the reservoir.

By applying the process reaction curve technique,the approximation of third order transfer function to reduced first order plus dead time system transfer function is obtained as,

The transfer function Gm(s)is known as the integer first order plus dead time system transfer function(I-FOPDT).On analyzing the FOPDT transfer function,it is evident that the system has a large time constant and time delay.

3.1 Fractional order modeling

The approximation of fractional order first order plus dead time model from third order transfer function is obtained using FOMCON toolbox[Aleksei,Petlenkov and Belikov(2011)].The procedure for obtaining the reduced order fractional FOPDT transfer function using FOMCON toolbox is explained as follows:

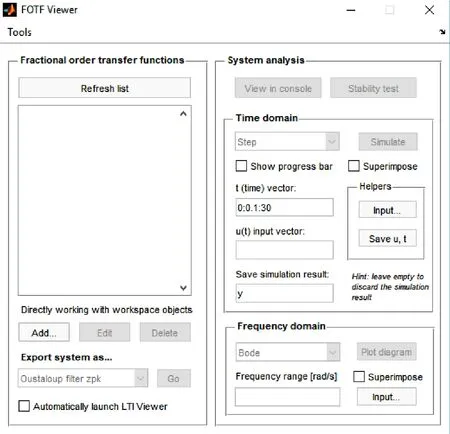
Figure 3:Graphic window

First the graphical window shown in Fig.3 is opened by typing the command fotf_gui.The higher order system transfer function is added and the response of the system is simulated for step input.The data is saved as id_1.

The time domain identification tool is opened by clicking tools and the step response data is uploaded and the identification method has to be chosen.The optimization is started choosing all this and after quite a few iterations the Fractional FOPDT model is obtained.In this work,the algorithm and simulation methods are changed until the identified model matches with the initial data.Here,oustaloup simulation method and Levenberg-Marquardt algorithm produced the best fit for the higher order process transfer function.Fig.4 shows the response of the absolute matching of the initial data with the identified model.The error norm is found to be 0.0031 and 99.97% fit with the given data.

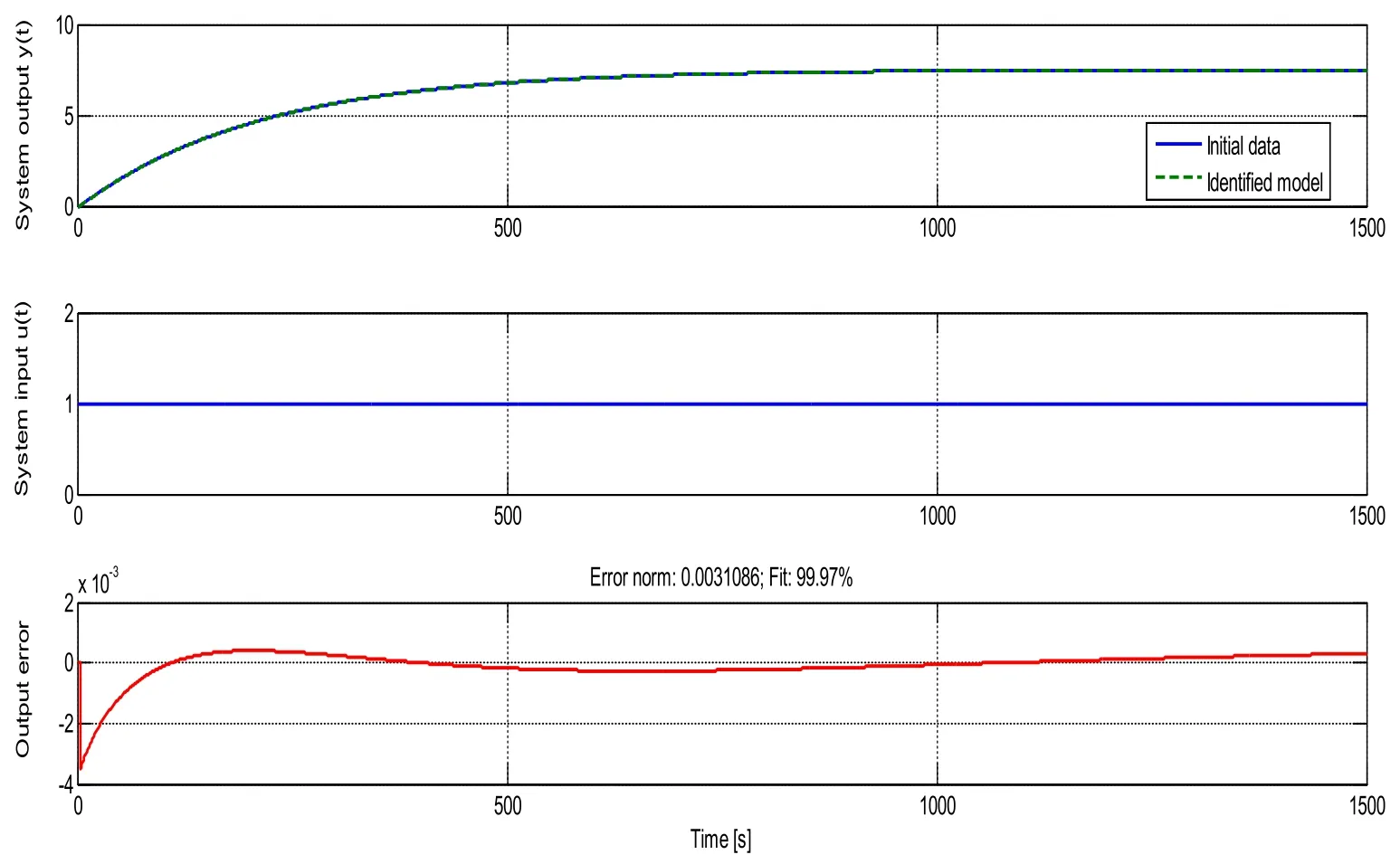
Figure 4:Fractional model validation

The transfer function obtained is as follows:

For the third order transfer function,step input is applied for Integer order FOPDT(IFOPDT)system and Fractional Order FOPDT(FFOPDT)system and the corresponding response is shown in Fig.5.From the response,it is evident that the fractional order transfer function matches closely to the third order transfer function and it is a perfect approximate model of the third order tank process.

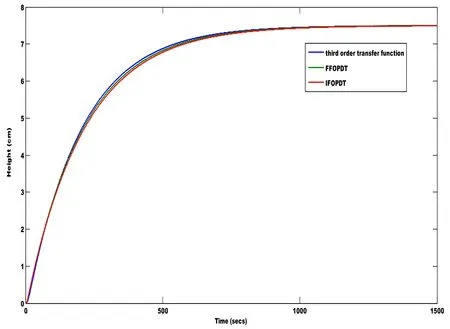
Figure 5:Comparison of time domain response of third order process with approximated IFOPDT and FFOPDT model

4 Smith predictor controllers and design procedure

Smith predictor is used for the compensating dead time for the process with larger dead time.Block diagram of general smith predictor controller is shown in Fig.6.The controller output is fed to process with large dead time and as well as to the process model.Once the Controller output is given to the process,the result obtained will be the actual output of the process.Likewise the controller output is given as an input to the process model excluding dead time.In our case,third order transfer function is considered as actual process and approximated FOPDT transfer function is considered as a process model.Then the difference between the actual output and process model with dead time is estimated.Then the predicted output of the process model excluding dead time and the estimated output is then summed up and it is given as a predicted feedback to the controller.As a result,faster response can be achieved and dead time of the process model can be improved.

Figure 6:Structure of smith predictor controller

In this work,four different configuration of smith predictor controller design is designed and implemented.Fig.7 and Fig.8 shows the smith predictor based PI controller design for integer order model and fractional order model respectively.Fig.9 and Fig.10 show the smith predictor based FOPI controller design for integer order model and fractional order model respectively.

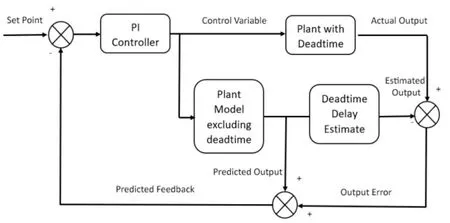
Figure 7:Smith predictor based PI with integer model

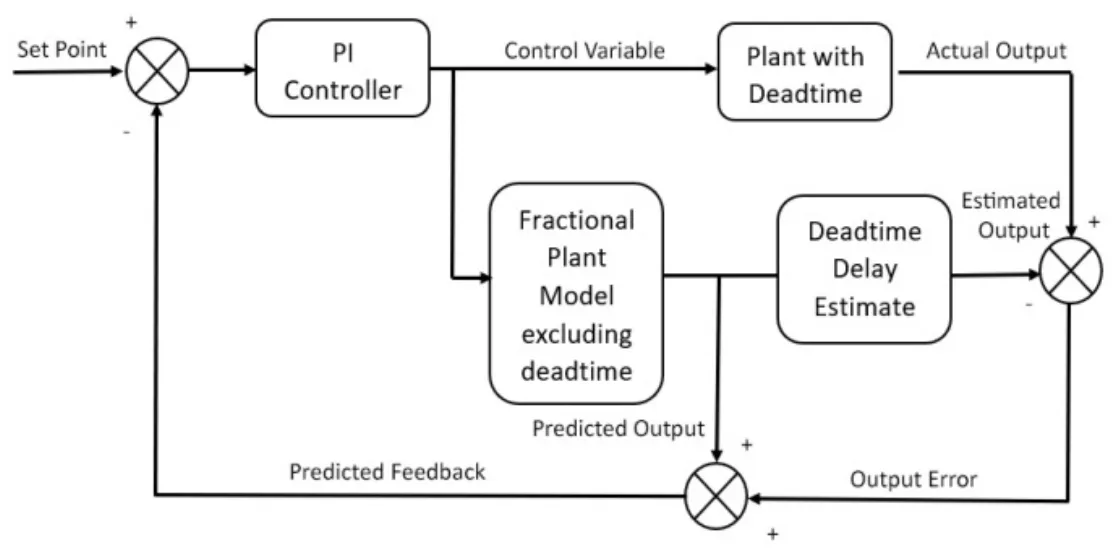
Figure 8:Smith predictor based PI with fractional model

Figure 9:Smith predictor based FOPI with integer model

Figure 10:Smith predictor based FOPI with fractional model

4.1 Smith predictor based controller design for IFOPDT system

The PI controller design using frequency response technique is done using the following steps:

The general representation of IFOPDT is of the form:

where,K denotes the Process Gain,τ the time constant of the process and L,the dead time of the process respectively.

1.Let s= jω.For the open loop transfer function,GIFOPDT(jω)determine the magnitude(A1)and phase(φ1).

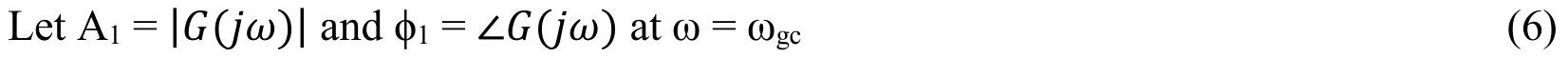
2.Determine the phase margin of the system and angle contributed to achieve the desired phase margin.

where,PMOLis the phase margin of the open loop system.

3. Determine the transfer function of the PI controller using the formula as:

4.2 Smith predictor based controller design for FFOPDT system

The general fractional Order FOPDT system takes the form

where,K denotes the Process Gain,τ the time constant,L the dead time and α is the order of the ‘s' term of the first order transfer function respectively.

The controller design using frequency response technique is done using the following steps:

1.Let s=jωα.For the open loop transfer function,GFFOPDT(jωα)determine the magnitude(A1)and phase(φ1).

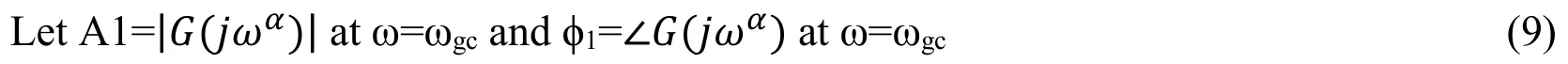
2.Determine the phase margin of the system and angle contributed to achieve the desired phase margin.

3.Determine the transfer function of the PI controller using the formula as:

4.3 Smith predictor based fractional controller design

The PI controller involves two parameters;the Proportional and Integral constants.Integer models are preferred because of the computational complexity in solving the fractional order differential equations.Even now,PI controller serve as the workhorses of many industrial automation.Improvements in the scheme are required for the quality and robustness of the control.But the real processes under control are fractional in nature.PI controller can be improved by converting the integer order controller to fractional order controller by incorporating a term λ.Hence smith predictor based fractional order proportional plus integral controller is employed for improving the control for time delay process.The transfer function of such a controller takes the form:

where,λ is the order of integrator.

The value of λ is varied between 0.7 and 1.5.The closed loop performance of the process for each lamda value is simulated and the best value is selected based on the performance criteria.

5 Results and discussions

For the reduced IFOPDT system transfer function Gm(s)shown below,the controller parameters are obtained by the procedure discussed in Section 4.1.

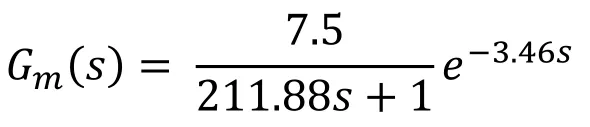
Bode plot is plotted for the above transfer function and gain crossover frequency,ωgcis found to be 0.036.

The values of Kpand Kiare found to be:

Kp=2.23,Ki=0.0613(For PMdesired=60°)

The value of ω is varied between the values from gain crossover frequency,ωgci.e.,0.036 to 0.15 to obtain an optimal controller parameter values.

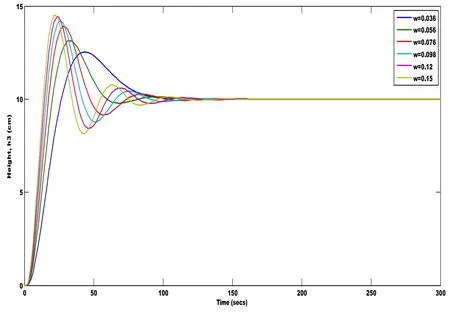
Figure 11:Effect of the closed loop response for varying value of ω(Integer model)

Fig.11 shows the closed loop response for different values of ω;by analyzing the performance indices it is found that the controller parameter value at ωgcitself is found to be optimum.

The controller values are obtained for the fractional model,as follows:

For the transfer function,Gmf(s),bode plot is drawn using fmincon toolbox and the value of ωgcis found to be 0.033.The value of ω is varied from 0.033 to 0.15.

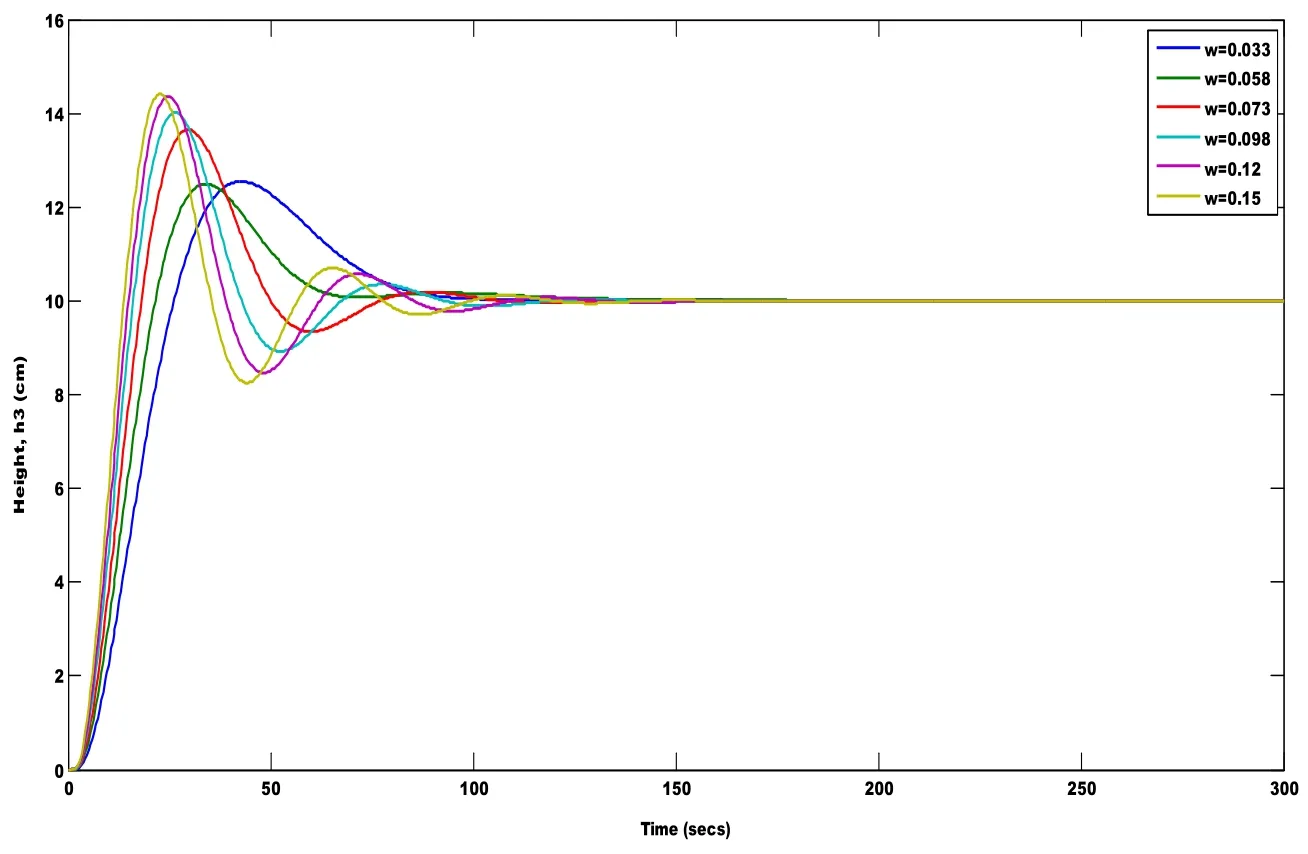
Figure 12:Effect of the closed loop response for varying value of ω(Fractional model)

Fig.12 shows the closed loop response for different values of ω;by analyzing the performance indices it is found that the controller parameter value at ω=0.073 is found to be optimum.

The controller parameters are obtained as mentioned in Section 4.2.The controller parameter values are found to be Kp=4.63 and Ki=0.218.

The closed loop responses of the process with integer model and fractional model is simulated and compared.Fig.13 shows the closed loop response of smith predictor based PI controller with integer model and fractional model.A disturbance is provided at 200 seconds and it is evident that smith based PI with fractional model is better than the other.

Figure 13:Closed loop response of smith based PI for integer model and fractional model with disturbance rejection

The performance indices are tabulated in Tab.3.It is clear from the table,the performance of smith based PI controller with fractional model is better than the smith based PI controller with integer model.

Table 3:Performance indices of smith based PI for integer model and fractional model

The set point is varied with the set values as 15 cm,35 cm,70 cm,61 cm and 8 cm at an interval of 200 seconds and the corresponding servo response of the proposed control system for integer model and fractional model is shown in the Fig.14.

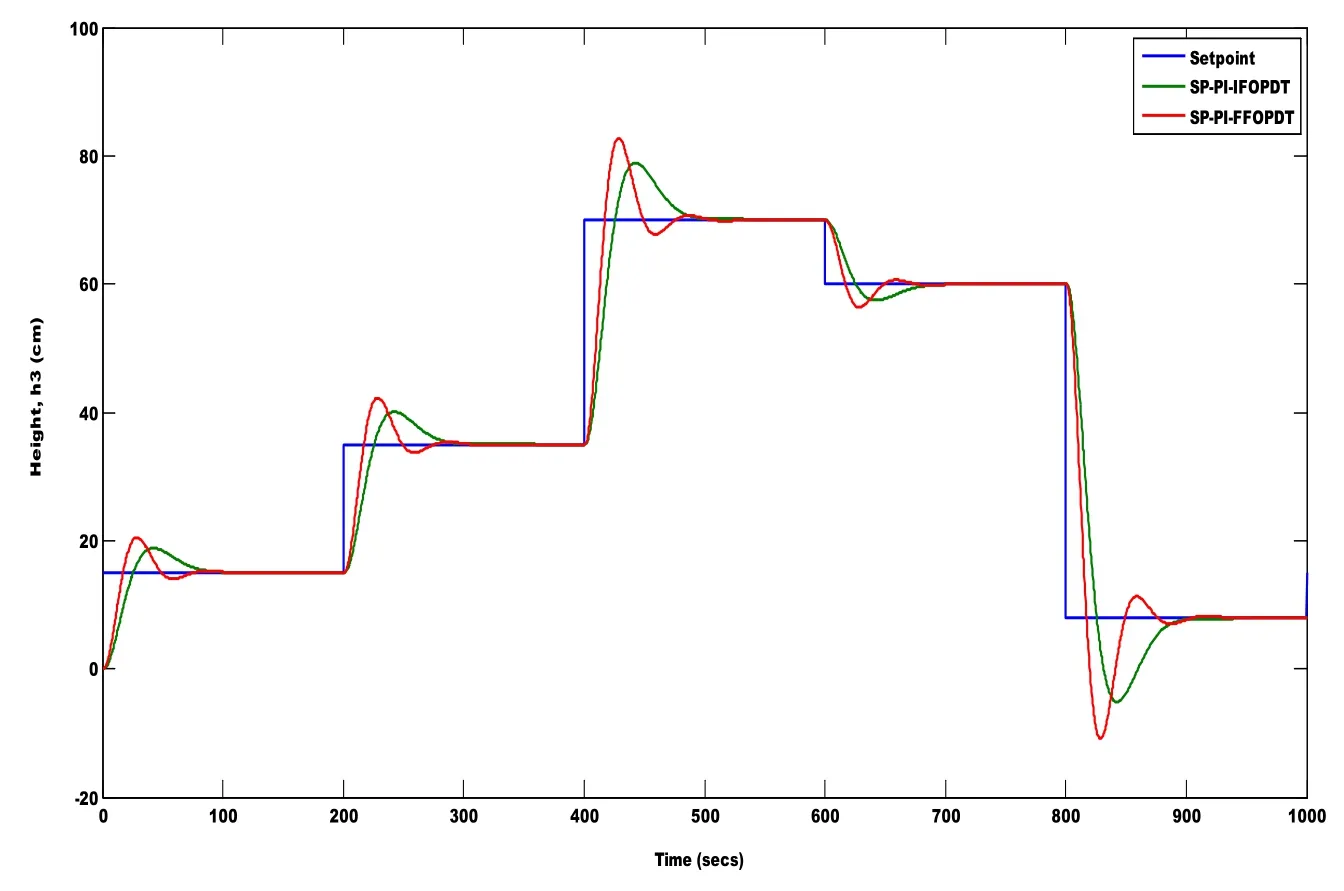
Figure 14:Height changes in the tank 3 for set point change at an interval of 200 seconds

The design of fractional PI controller requires three parameters to be identified i.e.,Kp,Kiand λ(lamda).The smith predictor based fractional PI controller is designed for the IFOPDT process transfer function by considering the value of Kp,Kito be 2.23 and 0.0613 respectively.The value of lamda is selected on the basis of closed loop performance indices value.

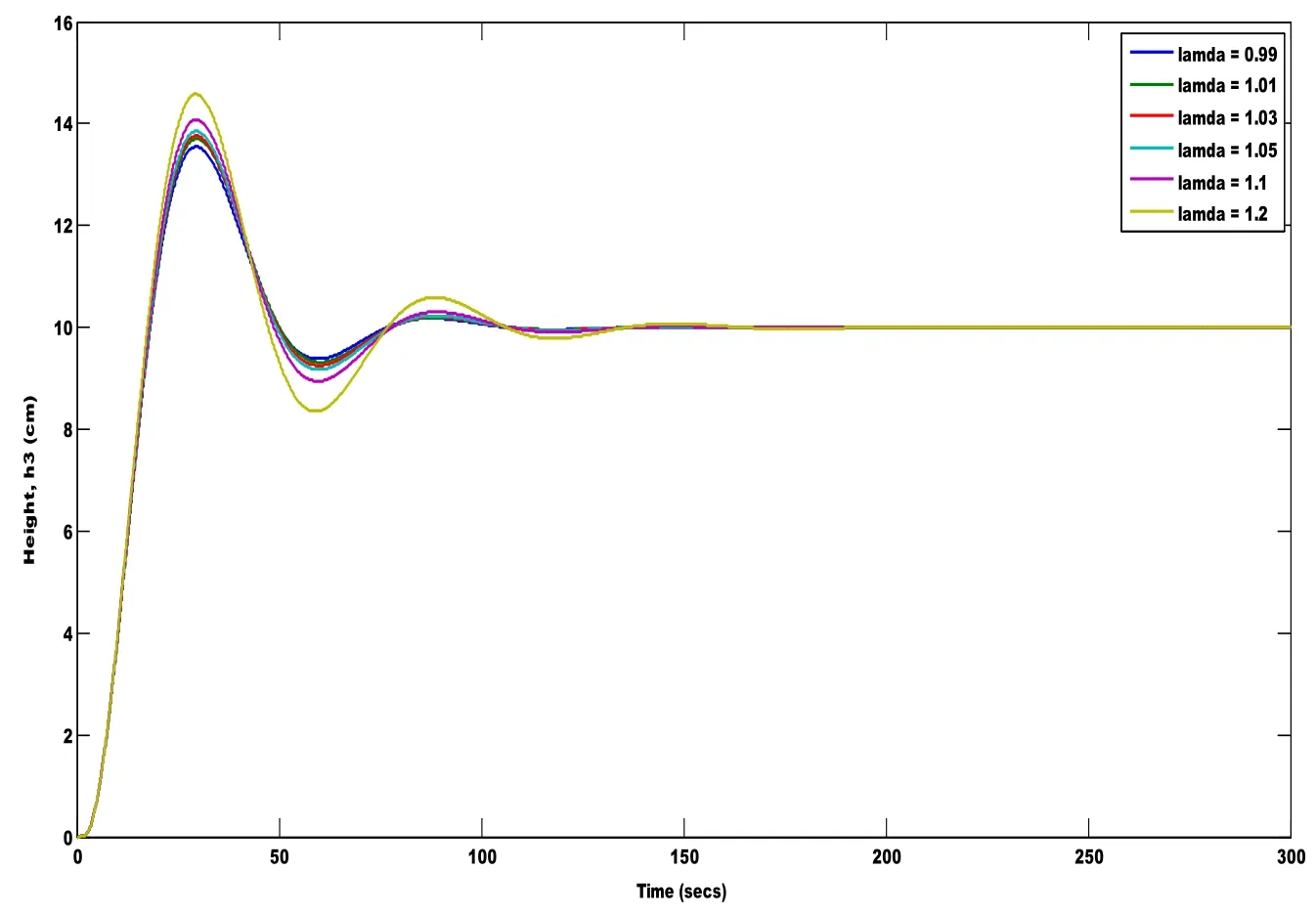
Figure 15:Effect of the closed loop response for IFOPDT process transfer function for varying value of lamda with fixed Kp and Ki

The Fig.15 shows the closed loop response of the process for various lamda values.The time domain performance indices are listed in Tab.4.

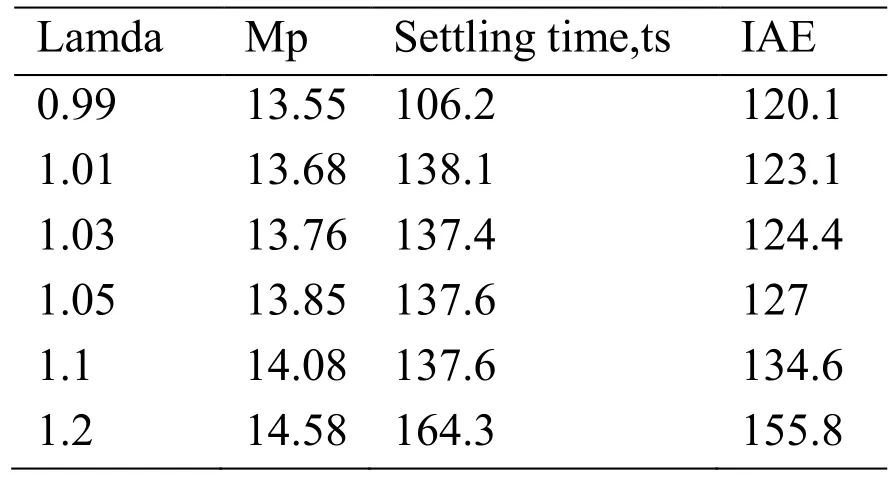
Table 4:Performance indices for various values of lamda

From the Tab.4,it is evident that the performance indices holds good for lamda equal to 0.99 hold good for the IFOPDT process transfer function.Similarly smith predictor based fractional PI controller is designed for the FFOPDT process considering Kp=4.63 and Ki=0.218.

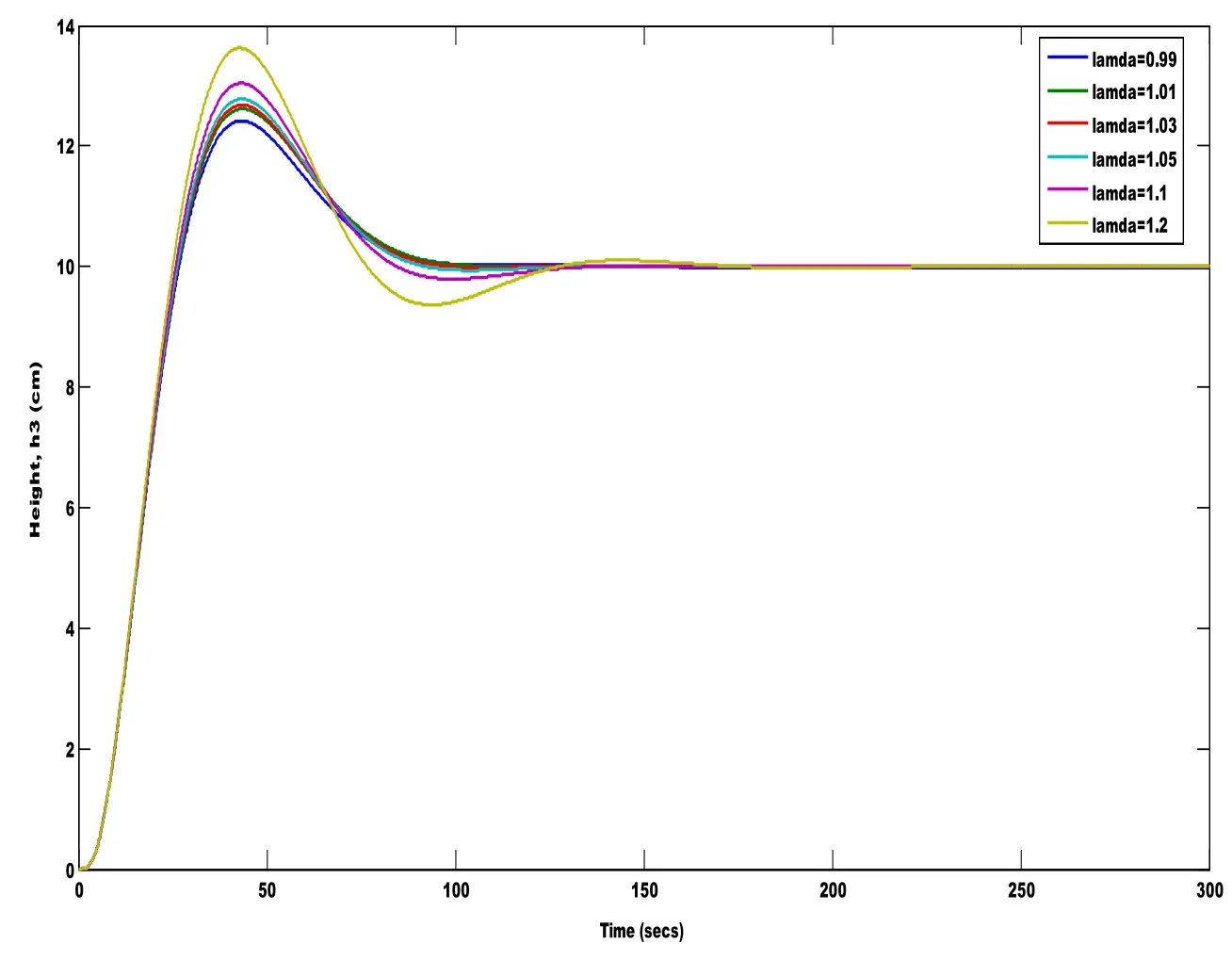
Figure 16:Effect of the closed loop response for FFOPDT process transfer function for varying value of lamda with fixed Kp and Ki

The closed loop response for various values of lamda is shown in Fig.16 and the corresponding performance indices are listed in Tab.5.It is seen that the performance is better when value of lamda chosen to be 0.99.

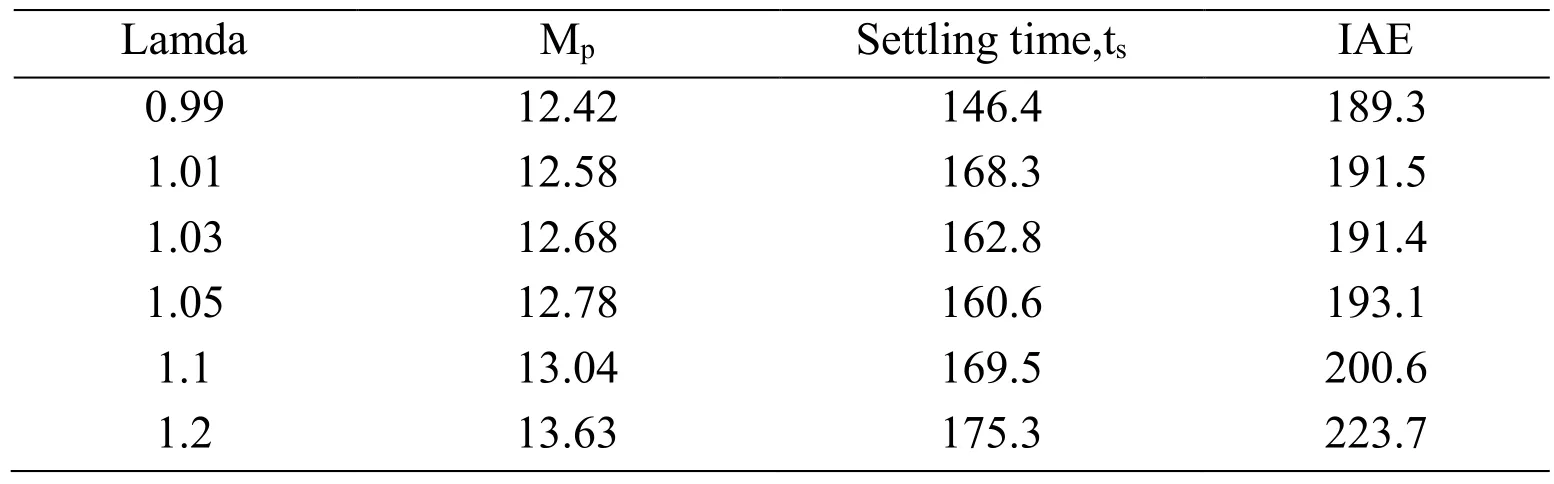
Table 5:Performance indices for various values of lamda

The closed loop responses of smith based FOPI controller for IFOPDT and FFOPDT transfer functions are simulated and compared.Fig.17 shows the comparison of closed loop responses.A disturbance is provided at 200 seconds and it is evident that smith based FOPI with fractional model is better than the other and Tab.6 gives the corresponding performance indices.

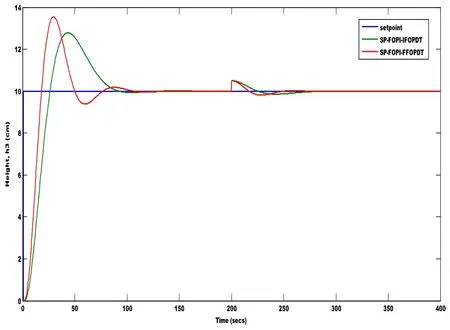
Figure 17:Closed loop response of smith based FOPI for integer model and fractional model with disturbance rejection

Table 6:Performance indices of smith based FOPI for integer model and fractional model

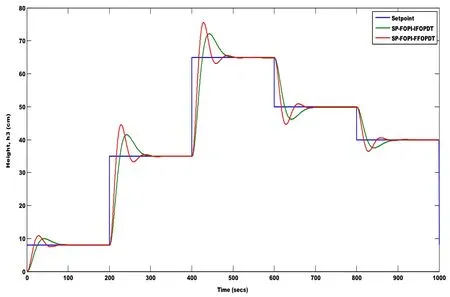
Figure 18:Height changes in the tank 3 for set point change at an interval of 200 seconds

The servo response of the designed control system of IFOPDT and FFOPDT transfer functions using smith predictor based FOPI controller is shown in the Fig.18,where the setpoint for the tank 3 of the three interacting tanks are fixed at 8 cm,35 cm,65 cm,50 cm and 40 cm at an interval of 200 seconds.

6 Conclusions

The interacting three tank process is modeled as a third order transfer function approximated as Integer First Order Plus Dead Time(IFOPDT)system and Fractional First Order Plus Dead Time(FFOPDT)system.Four different structures of Smith predictor controller are executed.The controller parameters are chosen based on their closed loop performances indices of the process.The performance indices for all the combinations of control structure are obtained and tabulated.From the results it is inferred that inclusion of an additional parameter in the controller and the process transfer function[i.e.,For,fractional PI controller,the parameters are Kp,Ki,λ,and Fractional FOPDT model,the parameters are K,τ,L and α]leads to the better performance of the process.Also the disturbance rejection is far better with smith predictor based FOPI designed for fractional model compared to other structures.