考虑维修时间的总质保需求预测模型

张瑞洁， 钟远光， 谢 维

(华南理工大学 工商管理学院，广东 广州 510006)

0 引言

制造商需要妥善地管理已售产品的质保服务来保持自身的市场竞争力[1]。质保服务是指售出的商品在质保期内出现非人为的故障或损坏时，制造商会为消费者提供相应的配件修理或替换服务[2]。质保服务不仅会影响消费者的购买决策，也会在一定程度上影响企业的发展，严重时还可能给企业带来生存危机。如发生在2010年因加速踏板质量问题所造成的丰田汽车召回事件，其中仅在中美两国召回汽车约237万辆，这一事件使得丰田公司损失惨重，它不但给使用丰田汽车的顾客带来了安全隐患，同样也对整个社会产生了一定程度的影响。而质保服务因消费者在质保期内可免费享用，直接增加了制造商的成本。据统计数据显示，质保服务所产生的成本可达制造商净销售额的2%～15%[3]。可知质保需求预测对于制造商是非常重要的。特别是对于投入市场的新产品而言，因制造商缺少质保维修数据等信息，在销售前准确的对新产品的质保需求做出预测，显得尤为重要。而且准确的质保需求预测，有利于制造商快速响应顾客的维修需求，提高顾客满意度进而增加企业的利润。

从本质上讲，新产品的总质保需求量取决于产品销量、可靠性以及质保策略等[4]。近20年内，关于质保服务的研究主要集中在，不同质保策略下产品维修服务成本的分析和基于质保需求相关数据的分析[5]。关于质保成本的估计，大多数文献所提出的模型都只能用来分析单个商品质保成本或长期意义上一个产品的总质保成本。Mamer[6]首先研究了单个商品的期望质保成本，并考虑了时间的价值，得到了对应的期望贴现质保成本。基于同一个问题，Kao and Smith[7]假设产品的寿命服从Phase-Type分布，他们提出的方法大大简化了期望质保成本的相关计算，提高了模型的使用效率。Chun and Tang[8]在此之后考虑了各种不同的质保策略，根据每个政策推导出了相关的贴现质保成本模型。在单个商品的基础上，Ja et al.[9]考虑了产品的不稳定销售过程，得到了产品总销量不确定下贴现总质保维修成本的期望和方差。在不考虑贴现率的情况下，赵文平等[10]做了最优质保期下的质保成本分析。当产品(视为系统)由多个部件组成时，其故障机制会变得更加复杂，对此，Baiand Pham[11]提出了串联系统贴现质保成本的期望和方差，Park and Pham[12]对该问题进一步深入研究，他们分析了现实中应用更广泛的k-out-of-n系统的质保成本。关于产品质保成本分析，Blischke et al.[13]做了非常全面的文献综述。因质保数据中包含了产品质量以及维修需求的大量信息，S.Wu[14]关于质保数据分析方面的研究做了详细的文献综述。此外，关于最优的质保策略如维修策略的选择以及质保期的确定等都被广泛的研究[15～20]。

在现有的关于质保的文献研究中，Park, M. et al.[21]也考虑了维修时间的影响，但是与本文的研究有很大的不同。首先，研究问题的角度不同。本文主要是站在制造商的角度，关注所出售的产品在质保期内产生的总的质保需求以及维修的成本，通过建立数学预测模型，对制造商管理零备件以及质保储备金提供理论参考。Park, M. et al.主要站在顾客的角度，定义了产品的生命周期以及维护时期，主要针对产品在质保期失效后顾客所面临的维护成本，建立了维护模型，并依据最小化平均成本率，求解出最优的维护模型。其次，所使用的质保策略不同。在质保期内，本文主要考虑的是免费的非更新最小维修策略。在该策略下，产品的质保期不可更新，是一个定值。Park, M. et al.的文章中采用的是可更新最小维修策略，产品的质保期会受到维修/替换行为的影响。也就是说在质保期内，故障产品在规定时间内未修好，则会进行替换，并产生新的质保期。最后是关于维修时间的处理不同。本文主要是采用复合随机过程中的交错更新理论来刻画维修时间对总质保需求的影响，该维修时间是随机的，并满足给定分布。而Park, M. et al.则是将维修时间作为质保规则中采用维修或替换行为的一个条件，文章中预先给出特定的维修时间，当产品所需的维修时间超出给定值时，则放弃维修，转而采用替换规则。和Park, M. et al.相比，本文的主要创新点是考虑了产品的动态销售过程，站在制造商的角度，对售出的产品所产生的维修总需求以及总成本建立预测模型。并且在刻画维修时间对维修需求的影响时，主要应用了交错更新理论，而非给出特定的维修时间将其作为一个选择质保策略(维修/替换)的条件来处理。

从上述文献中可以看出，以往关于质保需求预测的研究都存在一定的局限性：

(1)忽略了维修时间对质保需求预测的影响。首先，产品的维修是需要时间的，而且维修时间的长短，会直接影响消费者对维修商甚至制造商的选择。此外，维修时间也会对累积时间段内的产品的维修需求产生影响，而且维修时间也是产品质保期的一部分。以往的研究中都假设维修所需时间为零，但当产品的维修时间较长，且相应的维修费用和维修时间直接相关时，瞬时修理的假设就不合理了。故本文的第一个创新点就是考虑维修时间对产品的维修需求的影响。

(2)未考虑产品动态的销售过程存在的不确定性对质保需求的影响。对于制造商而言，产品都有一定期限的销售期，在这段时间内，不断销售出去的商品也存在损坏的可能，因此产品的动态销售过程会对质保需求的预测产生直接影响。故本文的第二个创新点就是在预测质保需求时，考虑产品动态销售过程。

本文主要是解决以上两个问题，即在前人的研究基础上，充分考虑产品的维修时间和销售不确定性对产品质保服务管理的影响，针对随时间变化的累积质保需求这个普遍存在的实际问题给出合理并且有效的预测理论，为广大制造商在产品质保服务管理中的短期和周期性维修资源和资金调配提供充分的理论依据和方法，创造具有社会经济价值的重要研究成果。

1 问题描述与假设

一个提供维修服务的制造商，当一件新商品被销售出去后，制造商提供给顾客一个时间长度为W的质保期，而该商品在质保期内所产生的故障次数与其相应的质保需求是等价的。与以往文献类似，本文也假设商品出现故障顾客会去维修的情况。即当商品出现故障时，顾客接受制造商的质保服务。这样的现象在现实中随处可见，因为这可为顾客节省一定的成本。同样，对于制造商，其往往只为出现故障的产品提供最小的维修服务。因此，本文假设制造商在质保期内提供的质保服务是免费的非更新最小维修策略(Non-renewable free minimal-repair warranty)，定义如下：

定义1(免费的非更新最小维修) 最小维修是指在商品失效之后，制造商免费用具有同样功能的零部件替换掉损坏的部分零件而使商品恢复原有的功能状态的过程。它强调维修的最小化，即只对出故障的那部分进行维修或更换，以此保证维修服务成本的最低。非更新是指商品的质保期是一个定值，商品质保期为W>0，如果一位顾客在0时刻购买了一件商品，且该商品在t∈[0,W]时刻出现故障，则制造商将会提供一个免费最小维修，且该商品剩余的质保期变为W-t。

在这个质保策略下，一个新产品存在一个确定的销售期L。一般情况下，新产品的销售时期是要比质保期长(L>W)；到时间，这个累积销售量N(t)为一个截距为L的非齐次泊松过程(Nonhomogenous Poisson Process, NHPP):

(1)

在现实中，制造商需要花费相当多的时间来维修故障产品，维修时间这一因素会影响产品的使用，并对维修需求产生直接影响。因此，这部分时间的影响是不可忽略的。本文利用随机过程中的交错更新理论来进行刻画维修时间的影响。考虑一件商品，一开始处于正常使用状态(‘on’)的时间长为X1，其第一次故障时间(‘off’)即维修所用时间为Y1。在完成第一次维修后，该商品又能够正常使用的时间为X2，以此类推，直到商品过了质保期。故可假设两个随机的时间序列，分别为{Xi}∞和{Yi}∞，两个序列独立同分布。并假设产品的生命Xi期是服从参数λ为的指数分布的随机变量，而维修时间Yi是服从参数为μ的指数分布的随机变量。用RD(W)来描述在[0,W]内一件商品所产生的质保需求。此外我们假设产品的销售过程和维修过程是互相独立的，则在销售期内，制造商所面临的期望总需求为：

TD(L)=E[N(L)RD(W)]=E[N(L)]E[RD(W)]

(2)

2 考虑维修时间的产品总质保需求

2.1 单件商品情形

在考虑维修时间的影响时，预测单件产品所产生的需求。制造商所需要解决的问题为预测单个售出的新商品的期望维修需求，即

E[RD(W)]

(3)

根据上文的描述，我们可以认为顾客维修商品的过程为更新过程。因此根据更新理论，可知一件产品在使用一段时间X1后，损坏并被送去维修花费时间为Y1，则这段时间X1+Y1可以看作一个更新周期。其更新周期X+Y的累积分布函数为FX+Y，更新过程在正常状态(‘on’)下的分布为FX，在故障状态(‘off’)下的分布为FY。则完成第n次维修所用的时间Sn为

定义H(W)为在W时刻所完成维修的次数，可得第n次维修时间Sn与维修次数H(W)的关系

H(W)=max{n:Sn≤W}

更新次数H(W)的均值即相应的更新函数为mX+Y(W)=E[H(W)]，目标是要估计一件产品在W内所产生的维修次数，即更新次数H(W)的在W内的均值，所以可得

E[RD(W)]=mX+Y(W)=E[H(W)]

(4)

我们先考虑一般情况，假设t为[0,W]内任意时刻，则参考Sheldon M. Ross[22]所著书中81页可知更新函数满足以下关系

(5)

(6)

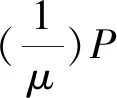
(7)

因为维修系统只有两个状态：工作状态或故障状态，所以可知P{在t时刻故障}=1-P{在t时刻工作}，根据转移概率函数Pij(t)=P{X(t+q)=j|X(q)=i}可得

(8)

所以单件商品在质保期W的维修需求为

(9)

我们假设单件产品的使用以及维修过程服从交错更新理论。并求出了X,Y服从指数分布时，单件产品的质保需求的解析表达式。此外，Xie W. et al.[23]在论文中也阐述产品损坏的时间服从指数分布的合理性。但当故障时间和维修时间服从一般分布时，我们可以利用仿真的方法很准确地估测质保需求。例如，假设X,Y服从指数分布，我们采用蒙特卡洛仿真的方法，首先生成满足给定分布的随机数，并依照交错更新理论的原理，计算出单个产品在质保期内的质保需求，对比了仿真求解结果和模型求解的结果，如下表所示，所有的误差率均小于0.06%，由此可见，采用仿真方法来估测质保需求是比较可靠的。

表1 指数分布下单件产品质保需求的仿真与模型结果对比

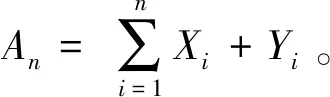
表2 在韦伯分布和正态分布下单件产品质保需求的仿真结果

2.2 多个销量情形

在求解产品在销售期所产生的总质保需求时，我们假设产品的销售过程与一件商品的维修过程是相互独立的，在产品可靠性一定的情况下，单件商品在质保期W的维修次数E[RD(W)]是一个常数。而我们的目标函数是

E[N(L)RD(W)]=E[N(L)]×E[RD(W)]

故需要预测产品的销量E[N(L)]。

(10)

求解微分方程并结合Λ(0)=0可得新产品的期望销量

(11)

故可得产品总质保需求

TD(L)=E[N(L)RD(W)]=E[N(L)]E[RD(W)]

(12)

2.3 参数μ、λ、W、L对总质保需求的影响

2.3.1 维修速率μ的影响

产品的维修时间主要由维修速率μ来决定，因此探讨维修时间对产品总质保需求的影响可转变为维修速率μ的影响。对μ求偏导可得

[W(λ+μ)(λ-μe-(λ+μ)W)+(μ-λ)(1-e-(λ+μ)W)]

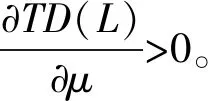
K=W(λ+μ)(λ-μe-(λ+μ)W)+(μ-λ)(1-μe-(λ+μ)W)

2.3.2 损坏频率λ的影响

在建立产品总质保需求模型时，参数λ可理解为产品的损坏频率，因为我们假设产品故障后，消费者一定会去维修，因此产品的损坏频率会直接影响到产品的总质保需求。根据模型可知参数λ和μ是对称的，因此可得

[W(λ+μ)(μ-λe-(λ+μ)W)+

(λ-μ)(1-e-(λ+μ)W)]>0

故可知新产品的维修需求是随着λ的增大而增大的。这显然和现实情况相吻合，一般而言，质保期都是以年为时间单位，λ表示一年商品所损坏的次数即损坏频率，如果取λ=2就表示商品每隔六个月就会出现一次故障。因此可知随着λ取值的增大，产品在质保期相应的维修需求量也越大。

2.3.3 质保期W的影响

伴随着科学技术的发展，智能产品接踵而来，人们渐渐被网络中的虚拟世界所迷惑。学生们的锻炼意识逐渐减弱，宁愿待在宿舍玩手机，也不愿进行室外活动。学生为了节省时间玩游戏或者学习，忽视了身体的重要性。这不仅会增强学生潜意识的惰性，还会降低身体机能，不利于学生良好的身心发展。因此，教育部提出体育教育信息化的发展，争取改变此现状，增进学生的健康，提高学生的素质，共同为体育教育信息化的发展而努力。

现实中，不同种类的新产品拥有着不同时间长度的质保期，产品质保期的长短不仅会直接影响消费者的购买欲望，也会对产品的成本产生间接的影响。对W求偏导得

因此可知，随着质保期W的增大，产品总质保需求随之增大。因为产品的销售期是一定的，也就是说在销量一定的情况下，质保期越长，总质保需求也就越大。这个增长主要来自于单件产品的维修量的增加。针对单件商品，单方面地增加质保期，无疑会导致故障频率的增加。因此企业在规定新产品的质保期时，应该权衡利弊。如果产品的质保期过长，会使得企业在未来面临更多不确定的维修需求，不但不利于企业合理地分配资金而且还会支付更多的维修费用，使得产品在定价方面失去竞争力；若产品的质保期较短，虽然在一定程度上会为公司节省了相应的维修成本，但会因为质保期过短的因素而失去消费者的信任，比如消费者在选择购买一台洗衣机时，两家公司的产品没有很大区别，消费者出去安全感的考虑，很可能会选择质保期较长的那个。因此企业应权衡利弊合理制定质保期，以确保产品有较低的维修成本的同时又具有市场竞争力。

2.3.4 销售期L的影响

时间长度L表示的是产品的销售期，销售期L对产品总质保需求的影响主要体现在对产品的累积销量E[N(L)]上，对E[N(L)]求导可得产品的销售率

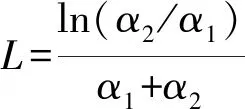
3 产品总质保需求成本

我们在上一小节中已经求出产品的总质保需求。如果能够准确预测产品在销售期内所产生的维修成本，制造商可以更加合理的分配现有的资金，更好地管理资金流。因此我们定义CW为每一次维修单件商品的预期成本，包括管理费用、材料费用、劳动成本等。显然，制造商总的质保成本可以表示为

TCW=CWE[N(L)]E[RD(W)]

(13)

因为，质保需求的总费用相当于维修需求的CW倍，显然参数λ、μ、W、L对产品在销售期内所产生的维修费用的影响与产品总质保需求是一样的。即总质保维修成本随着产品损坏频率的增大而增大，随着产品维修速度的增大而增大。产品的维修速度越快，即在整个销售期内，制造商所需储备的质保维修费用也就越高。而质保期以及销售期对总质保成本的影响更加直观，即产品质保期和销售期越长，相应的维修成本也就越大。

4 数值例子

为了更好理解上述内容，在这一章中，我们将用一些数值例子来反映产品的损坏频率、维修速度以及产品质保期和销售期对产品总质保需求的影响。此外，这些结果还可以用来指导制造商的生产计划等，通过合理地估计产品的质保需求，从而更恰当地分配制造商有限的运营资金。这些数值例子中一些参数的取值是参考Stefanka Chukova[25]以及Xie W. et al.[26]等的论文中所使用的数值，在此假定销售期L=5，并认为当产品的销售期到达5年时，制造商将会推出新一代的商品而不再出产旧产品。并且认为质保期W是以年为单位且取值大小不超过L。

4.1 参数μ、λ、W、L的敏感性分析

4.1.1 参数μ、λ的敏感分析

我们在上文中已经求导得出产品的质保需求随着维修速率的增大而增大。从图1中，可直观地看出随着产品维修速度的加快，产品的维修需求也随之增加，但增加的幅度逐渐减小，最终趋于一个定值。因维修速度是和维修时间成反比，维修速度的增大，表明修理一件商品所花费的时间越短，则在质保期W一定的情况下，产品的工作时间也就越长，因此故障频率会相应地增加；当维修速率μ趋于无穷大时，可认为维修时间为零，这时总质保需求变为销量与损坏率的乘积。图2表明损坏频率λ增大时，产品的总质保需求也随之增大，但是其增长速率逐渐减小，这是因为当损坏频率持续增加时，产品的维修速率成为主要的限制因素，在质保期一定的情况下，产品维修速度不够快，很多故障的产品不能及时维修好，产生积压，最终产品的质保需求趋于一个定值。此外，维修商品是一件耗时又耗钱的事情，一般情况下，产品的损坏频率是很大程度上可以由制造商来确定，即适当提高产品的可靠性，可以大大降低商品在质保期的维修需求。

因此，制造商如果想在一定程度上控制商品的质保需求量，一方面可以提高产品的可靠性，即降低商品的损坏频率λ；而另一方面可以适当延长产品的维修时间。虽然产品维修时间越长，维修需求越低，但是过长的修理时间会对产品的使用者产生较大的成本，特别是对于那些大型的生产机器，停机一天的造成损失非常大。因此制造商在确定维修速率时，应权衡利弊，以防丢失部分消费者的信任。

图1 总质保需求随维修速率μ的变化

图2 总质保需求随损坏频率λ的变化

4.1.2 参数W的敏感性分析

目标函数是预测新产品在整个销售期L内所产生的总质保需求，图3给出了总质保需求随W的变化，可以很明显地看出，在损坏频率λ和维修速度μ不变的情况下，产品总质保需求随质保期W的增大而增大。此外随着销售期L的增加，总的质保需求也是呈现递增的趋势，但是增加的幅度开始较大，而后减缓，这是因为新产品销售率先增大后减小的缘故。根据以上分析可知产品销售过程会对总质保需求产生影响。总所周知，现在市场竞争较为激烈，许多新产品还没进入成熟期已经被其他同质性产品所取代，此时销售期L比较短，因此对于这类产品而言，制造商最好缩短它的质保期，以减少总的质保需求；而现实中有些新产品的销售期很长，且是终身保修的，针对这些产品，制造商可以通过提高产品的可靠性，来减少总的质保需求。此外，制造商还可以根据新商品投入市场前期的销售记录来拟合产品的总质保需求，并根据不断增长的销售数据，及时地调整总质保函数的相关参数，进而得到比较准确地总质保需求，为制造商恰当地安排生产计划以及资金的合理分配提供一定的理论指导。

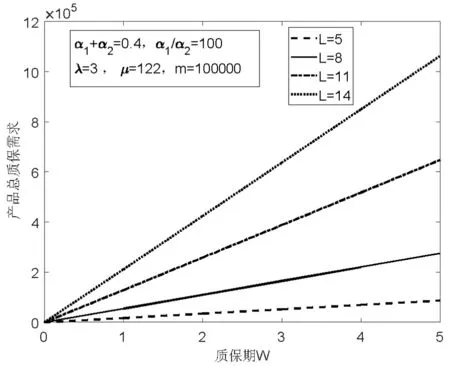
图3 总质保需求随质保期W的变化

4.1.3 参数L的敏感性分析

图4 产品销量随销售期L变化

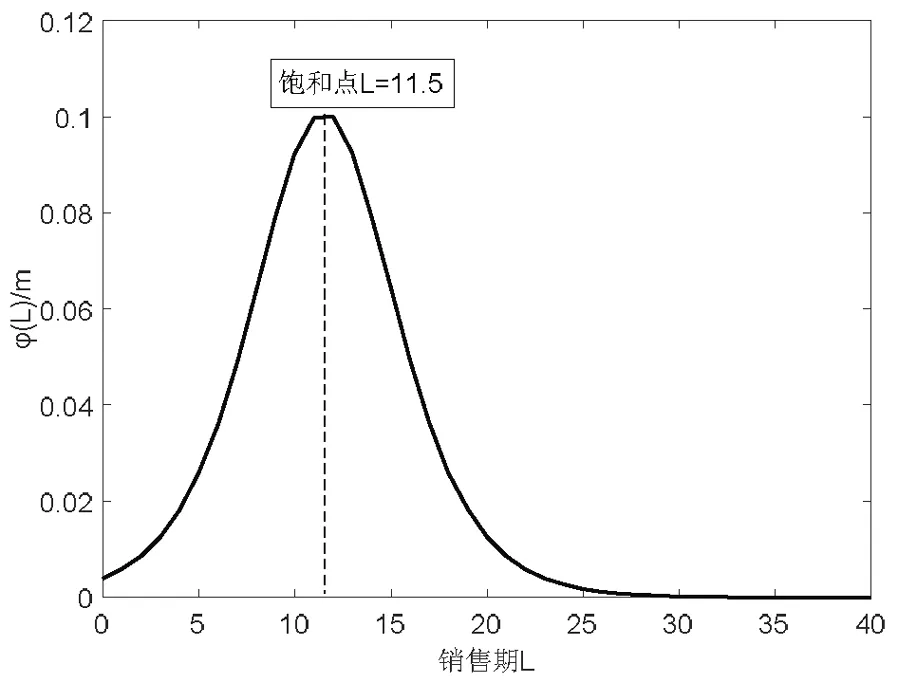
图5 产品销售率随销售期L的变化

4.2 参数μ、λ、W对总质保成本TCW的影响

图6 产品总质保成本随损坏频率λ以及维修速率μ的变化

表3 质保期内预期的总质保成本,μ=92,CW=30

表4 质保期内的预期的总质保成本,μ=122,CW=30

5 总结

本文主要站在制造商的立场上，研究了新产品的总质保需求受产品的维修时间和产品的累积销售过程的影响，并建立了相应的数学模型预测制造商在销售期内所面临的维修需求。主要的研究成果如下： (1)切实考虑商品在维修过程中所花费的时间这一因素，利用随机过程中的交错更新理论，首先对售出的商品在质保期内所产生的维修需求建立了数学模型。并在理论上分析了产品的损坏频率、维修速度以及质保期的长短对商品的维修需求所带来的影响。因为一般情况下，制造商在生产产品时，一批产品可靠性不会有很大的变化，这也表明产品的损坏频率大致是个定值。故对于一些消费者对产品维修所花费的时间不敏感的商品(消费者存在该商品的替代品)，制造商可适当降低商品的维修速度以减少该商品在质保期内的维修需求；此外制造商应合理地制定质保期，可选择满足国家规定或者达到消费者满意度的最小的质保期W，以确保产品有较低的维修成本的同时又具有市场竞争力。 (2)在计算总质保需求时，充分考虑了产品在实际中随机的销售过程，利用NHPP-Bass model模型进行拟合，并结合单件商品在质保期的维修需求，进而得出产品在整个销售期内所产生的总质保需求。并根据模型求解的结果，为制造商提供以下建议：首先，对于一些终身保修的新产品，一般都是一些大型的而生产机器，购入成本较高且产品的使用寿命较长。制造商如果想要降低其质保需求，则需要在生产过程中，严格控制产品质量，提高产品的可靠性，既要尽量降低产品的损坏率，考虑到停产造成的巨大损失，因此也要提高维修产品的速率。其次，制造商还可以根据总质保需求的预测模型，利用新产品投入市场的前期的销售数据以及维修需求数据不断调整该模型的参数，并结合模型总产品的质保需求预测，合理地制定维修配件的生产与管理，恰当的分配资金。

本文的不足之处是假设产品的销售过程与单件产品的维修过程是相互独立的，未考虑产品销售时间点的影响，只预测了产品在质保期内产生的质保需求。在现实生活中，因为每一个销售出去的产品都会产生随机的维修需求，因此制造商在任意时间点所面临的维修需求是每一个随机售出产品可能产生的维修需求之和，也就是说总的维修需求还会受到产品销售时间点的影响。在后续工作中，我们会考虑产品销售时间点对维修需求的影响，通过考虑随机销售过程以及随机维修过程在任意时间段的叠加效用，求出制造商在产品整个生命周期内任意时间段所面临的质保需求，进而对制造商管理任意时间内的零备件以及质保储备金提供理论支持。