河道型水库水温结构变化特征的研究方法探讨
2019-06-11阳振华
阳振华
(安徽省水利水电勘测设计院 合肥 230000)
1 研究背景及目的
我国拥有丰富的水电资源,大量已建、在建和规划兴建的河道型水库的运行为当地经济和社会发展发挥了巨大的作用,但另一方面,也对库区水体内及下游生态环境的健康发展带来了不利影响,如河道功能退化、水生生物生境破坏、洄游性鱼类数量减少等。河道型水库中水体的水温分布情况影响着库区内及其下游的生态系统,涉及到水库下游水质、水生微生物、水生动物和农作物等方面。因此研究水库蓄水后水体的水温分布结构和规律,不但对库区内生态系统具有重大意义,而且对水库下泄水流给下游的水生生物及其工程自身造成的影响等方面都具有积极作用。
2 各因素对库区水温的影响机制
(1)河道型水库内水深处流速缓慢,热量传输能力下降,进入初夏后,库面水受到太阳辐射而增温密度减小,停留在温度较低、密度较高的下层水之上,在风和波浪等作用不足以让水体在垂向上混合的情况下,很有可能出现水体的温度分层现象。正是因为这些原因,兴建大坝挡水很有可能使得水库中水体在特定的季节形成局部的水体水温在垂向上的分层现象。
(2)在坝前水体的水温全年不出现分层现象情况下,在无其他特殊情况时候,大坝的下游水体水温与天然河道中水体水温没有较大区别,而仅当在坝前水体的水温形成稳定分层情况下,大坝的下泄水温有可能高于或者低于天然河道的水温。
3 水温分布的类型及判别方法
水库水温分布按照特点分类一般可以分成三种:水温稳定分层型、水温混合型和水温过渡型。在水温分层比较稳定的水温稳定分层型水库中,水体水温由上至下可以划分为温变层(Epilimnion)、温跃层(Metalimnion)和滞温层(Hypolimnion)三层。图1 展示了典型分层型水库在各处水温均高于4℃的情况下垂向水温分布情况。温变层水体水温随气温变化而迅速变化,温跃层水体水温在垂直方向上具有较大的梯度,而滞温层水体水温分布基本均匀;混合型水库水体水温在垂向上分层现象不明显,水体在垂向上水温分布平均,全年水温变幅较大;过渡型水库的特点介于前两者之间,比较少出现不稳定的分层现象。
比较常用的水库水温分布情况判断方法有多种,如参数α-β 法、Norton 密度佛汝得数法和水库宽深比法等,其中前二者在使用时不仅方便而且结果也比较准确,对计算的结果运用水库实测水温资料进行对比,发现其预测的结果与实际情况比较接近。
3.1 参数α-β 法
这种方法为日本学者提出,并作为国内判断一个水库是否分层的主要根据得到广泛的应用。
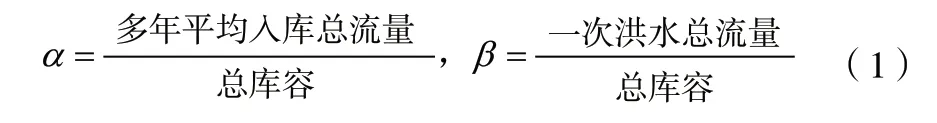
当α 小于10 时,水库中水体的水温分布规律符合稳定分层型特点;α 大于10 而小于20 时,归类为过渡型;α 大于20 时,为混合型水温分布水库。一般情况下,得出α 的值就可用来初步判断水库是分层型水库还是混合型水库,然而洪水条件改变的情况下,分层型水库也有向混合型水库转变的可能,故采用β 值判别法作为第二判别标准。对于水温分布分层型水库而言,假设遇到β 大于1 的大洪水,那么洪水作用会打破水库原有的水温分布结构形势,在短暂的时间内,使水库的分层类型变成混合型,而遇到β 小于0.5 的洪水时,水温结构一般不会出现显著变化,这样的判别方法适用的水库特点为全年中枯水季节和洪水季节区别不是太大、洪水频发而且洪水水量不是太大。
3.2 Norton 密度佛汝得数法
20 世纪70年代美国学者提出用密度佛汝得数来判断水库水温的分层特征,密度佛汝得数作为惯性作用和因水体的密度不匀均引起的浮力的比值,Fr用下列公式表达:

式中:L 为水库长度,m;Q 为流入水库的水流流量,m3/s;H 为水库的平均水深,m;V 为库容大小,m3/s;E 为水体标准化的竖直方向的密度梯度,E=Δρ/(ρ0H);g 为重力加速度值,m3/s。
根据哥伦比亚河上和田纳西流域管理机构的水库水温方面的实测数据:Fr>1.0 时水库为完全混合型;0.5<Fr<1.0为混合型,0.1<Fr<0.5 为弱分层型,Fr<0.1 时为稳定分层型。在采用参数α-β 判别法判别出水库水温结构为过渡型时,可运用佛汝德数判别法对水体水温分布情况作出进一步的判别。
3.3 宽深比判别方法
水库平均宽度与深度的比值判别法公式为:

式中:B 为水库水面平均宽度,m;H 为水库平均水深,m。在H 的取值大于15m 时,当R 大于30 时水库水温分布为混合型,当R 小于30 时水库水温分布为分层型。
3.4 其他方法
现阶段不仅有以上几种方法,也有其他方法如将人工神经网络理论相结合的方法、运用多目标决策计算的模糊模式判别法和基于回归分析技术、解析法等。
4 水库水温预测的方法
在我国,水库水温的实际观测始于20 世纪50年代。80年代比较有代表性的是东北勘测设计院的张大发和水利水电科学研究院朱伯芳通过对已有监测数据的中型以上的水库水体的温度实际测量温度数据进行分析,综合和归纳了水库水温的分布特征,在90年代中期提出了预测水库水温的不同计算理论和方法,成为目前水库水温估算最常用的方法。
4.1 东北勘测设计院张大发法
这种方法的应用需要两个参数,一个是水库水温计算的月份水库表层水体月平均水温,另一个是水库库底水体水温的月平均值,根据这两个参数就可以计算整个水库的任何深度的该月平均水温分布,这种方法的计算表达式为:

式中:Ty为在计算月份水深y 处的月平均水温,℃; Ta为水库表层水体的当月平均水温,℃,可以通过纬度相关估算;Tb为水库水温估算月份的底部水体月平均水温值,℃,相对水温分层型水库和水温过渡型水库,整个年份内各个月份之间差值很小,可用常数库底年平均水温来代替,水库的水深和纬度是影响它的两个相关因素,并可用纬度—水温关系进行估算;m 为月份。
这种方法已被规范采用,给出水库库底和库表的月平均水温就可以方便地预测水库水温分布情况,运用气温水温相关法或维度水温相关法就可以推测水库库底、库表水温。需要指出的是,运用时需要考虑工程所在地的气候、海拔和工程特点等各种情况,而且运用此方法得出的结果并不精确,无法运用到具有代表性的分层型水库的更小时段的水温预测,如逐月或者逐旬的水位分布预测。仅适用于低海拔和库容不太大的中小型水库的逐月水温的平均值的粗略估计。
4.2 水利水电科学研究院朱伯芳法
有学者(如朱伯芳)认为水库水温分布变化规律以年为单位呈周期性变化。水库水体的温度变化幅度的大小随着水深的增大而减小:水库表层水体的温度变化比较剧烈,当深度加大,对应的水体温度变化更小,底部水体的温度常年在一个很低的温度。发现不同深度的库水温度变化符合余弦函数特点,表述如下:
(1)任意深度的水温变化

(2)任意深度的年平均水温

(3)任意深度的水温年变幅

(4)水温变化的相位差

式中:y 为水深,m;t 为时间,月;T(y,t)为深度y、时间为t 时温度,℃; Tm(y)为水深在y 处的年平均温度,℃;A(y)为水深在y 处的温度年变化幅度,℃,可通过水库表面水体的水温年变化幅度A0求得;t0为从年内气温最小值到气温的最大值的时段,月;ε 为水温规律性变化的相位差,月。
5 水库水温预测的数值模拟研究
数学模拟计算模型是在综合考虑可能引起水库水温变化各种因素的基础上,充分运用包括热量、动量和能量等方面的平衡方程建立起来的,不仅精确度比较高,而且节约时间还能够节省费用和人力,运用数学模型计算水库水温越来越成为水库水温研究的主流,且应用范围得到了扩大,河道型水库水体水温分布计算的数学模型从维数上分:一维数学模型、二维数学模型和三维数学模型。
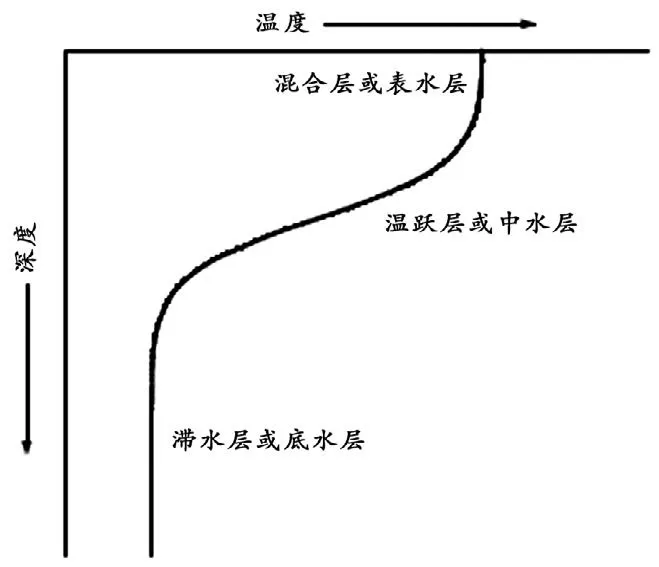
图1 分层型水库的垂向水温分布示意图
一维水温模型考虑了对水库水温分布的多种因素,如水库的入流和水库水面的热交换情况等,计算的一些假设如等温面假设基本符合应用对象的实际情况,也得到了广泛运用和推广,但该模型因忽略了温度和流速等在纵向和垂向方向上的变化而不适合水面较宽或纵向水温变化明显的水库。
1986年美国陆军工程兵团水道实验站和波特兰州立大学共同开发了二维纵深方向的水动力学和水质数学计算模拟模型CE-QUAL-W2,该数学模型是迄今发展最为成熟和完善的二维水动力学水质数学模型之一,并在水库、湖泊和河流等水体的水温分布研究和水质研究中得到广泛的应用,随后该模型改进了水体在垂向上的扩散系数的计算方法和表层水体热交换的计算,随后相继推出了CEQUAL-W2 Version 2.0、Version 3.0 等版本。丹麦水力研究所(DHI)研制MIKE 系列水质模型软件中的MIKE21 模型也是非常成熟的平面二维水质模型,也能较好地模拟水库、湖泊、河流、河口和海湾的水温分布■
