就题取材 大放异彩
——一道高三期中试题的创新解法及其赏析
2019-06-11许培琳
许培琳
江苏省连云港外国语学校 (222006)
高考(模拟)试题设计力求具有情境熟,入口多,方法灵活多样的特点,同时要求对数学知识的考查既全面又突出重点.小题的设计以短、平、活为主,小题的解答以快、简、准为原则进行,能更好地体现学生对知识的掌握程度与学生的应试能力,因此小题也颇有探析的价值.本文以2019届姜堰中学、淮阴中学高三期中联考第13题为例进行解析.
1.试题呈现
已知圆O:x2+y2=1,过定点A(3,0)的直线l与圆O相交于B,C两点,且B,C两点均在x轴的上方,若OC平分∠AOB,则直线l的斜率为.
这道题是填空压轴题,在直线和圆位置关系等知识的交汇处命制,即考查了弦长公式、角平分线定理、向量共线定理、余弦定理、面积公式、三角函数的定义、两点斜率公式等基础知识的应用,又考查了直观想象、逻辑推理、数学运算等数学素养,突出了能力立意,彰显了数学思想方法.看起来背景熟悉、平淡无奇,实际上内涵丰富,解题思路较多.从不同的角度去审视它可以得出一系列优美解法,为学生提供了多样化的选择,是一道匠心独运的好题.
2.解法探究
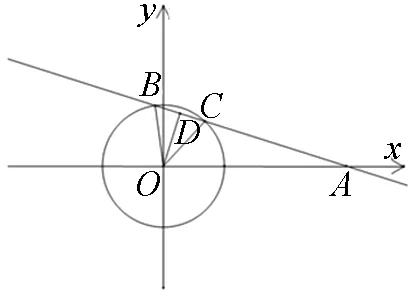
图1
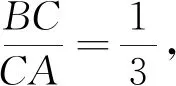
解法1:由OC平分
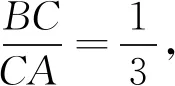
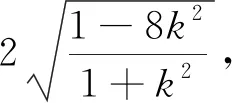
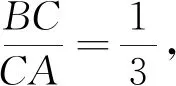
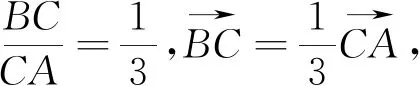
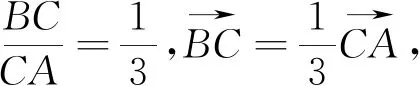
回过头来看,出现在ΔAOB中的底OA=3为一定值能否利用面积公式和结合余弦定理,于是得到解法4.
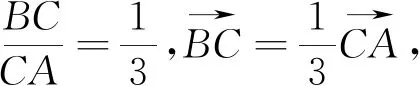
在ΔAOB中能否利用几何方法结合三角函数定义求出斜率?
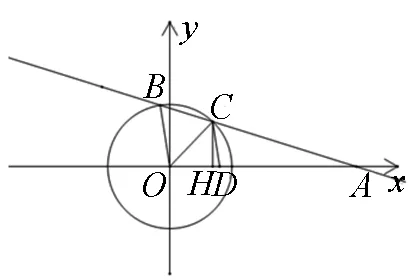
图2
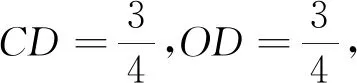
由于题目的条件是在单位圆中,我们联想到用设参数方法求解,得到解法6.

3.变式探究
在寻求解法的同时,领略考题的本质,挖掘其深刻的内涵,作出一些必要的延伸,充分发挥试题的功能和作用.
变式1 已知圆O:x2+y2=1,定点A(3,0),过点A的直线l与圆O相交于B,C两点,且B,C两点均在x轴的上方,若点C恰好是线段AB的中点,则直线l的斜率为.
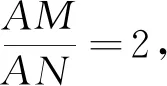
变式3 在平面直角坐标系xoy中,已知点O(0,0),A(0,3),如果圆C:(x-a)2+(y-2a+4)2=1上总存在点M,使得MA=2MO,则圆C的圆心横坐标a取值范围是.
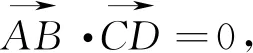
4.亮点赏析
4.1 基于教材素材,立足基础知识
本题的素材来源于苏教版必修2P117页习题2.2(2)第3题,体现了考试命题“源于教材,高于教材”的指导思想.题面简洁,题意新颖,在诸多基础知识和基本方法的交汇处命制,表述通俗,意图清晰,难易适中,构思巧妙,符合学生的认知规律,有良好的区分度.试题立足教材,以教材中的习题为题根,给学生以亲切感,同时对教师的教和学生的学起到很好的导向作用.
4.2 解题思路宽泛,突出通性通法
本题的解法可谓灵活多样,可以从单纯的解析几何的通性通法入手,也可以从向量视角入手、还可以利用三角函数的知识解决,或者引入参数,或者从平面几何知识入手.从不同视角,不同的高度都可以得到解决问题的思路,但不同的思路,运算的繁简程度也不尽相同.突出通性和通法的考查是一大亮点.在解题教学中要把通性通法的训练作为重头戏,要让学生独立思考、尝试解答,通过展示和交流使学生,在问题求解中掌握通性和通法.
4.3 着眼数学素养,考查学习潜力
本题很好地体现了高考对数学核心素养和学习潜力的考查,特别是对运算素养的考查体现的淋漓尽致.许多学生解题思路清晰,解题目标也很明确,但是在运算上遇到了阻碍,陷于繁杂的运算中不能自拔,不能选择适当的方法简化运算,导致功亏一篑,造成遗憾.提高数学核心素养,培养学生学习潜能尤为重要,应该引起教师的高度重视.
5.结束语
在解题教学中,教师要紧扣课程标准,着眼教学内容、教学理论、教学实践与数学核心素养的有机结合,以问题为导向,不断探索,引导学生从本质上认识数学,从策略上优化数学解题,从方法和思想上发展数学的理性思维,为学生营造良好的数学教育环境,使素养之花在学生心中自然绽放,让数学课堂精彩纷呈.
