空调PTC加热器热分析与工艺参数优化

(浙江工业大学 机械工程学院，浙江 杭州 310014)

空调PTC加热器是目前最安全可靠、效率最高和最清洁的电加热器。专家预计，随着电能成本的进一步降低，PTC加热器的市场需求将会有更大幅度的提高。目前，常用的空调PTC加热器主要由PTC发热芯和散热结构两部分组成，常应用于空调辅助加热和取暖器，功率一般在1 000 W以上。由于空调PTC发热片的阻温特性，PTC加热器会产生类似恒温器特点，通过PTC加热器结构设计，提高电能利用效率，是当前PTC加热器设计和制造领域的主要研究内容之一。盛健[1]对3 种空调电辅加热技术进行了比较，结果表明空调PTC加热器成本相对较高，但制热启动快，热功率大，是相对更优的电加热器。Laor等[2]给出了翅片的结构通用性传热微分方程。陈群等[3]研究了最小热阻原理在对流换热过程分析与优化中的适用性。李顺达等[4-5]基于翅片效率，对矩形板翅式换热器结构参数对传热性能的影响进行了分析，结果表明翅片厚度越大，翅片效率越高，单元间距越大，翅片效率越低。夏萍等[6]使用fluent对汽车用PTC加热器的最佳使用性能与湍流强度和流速的变化关系进行了仿真模拟，并根据模拟结果对汽车用PTC加热器的工艺参数进行优化，结合实验，验证了模拟的可靠性。

但是以上研究均是针对散热结构的分析优化。对于空调PTC加热器从热源至散热结构的整体换热能力尚未有研究。同时家用、车用和工业用的空调PTC加热器从结构到设计性能都有着巨大的差别。笔者将在前人的基础上，以空调PTC加热器为研究对象，利用数值计算和仿真模拟的方法对PTC加热器的加热芯与散热结构进行热分析，并根据分析结果进行结构优化。最后设计实验比较优化结果与原有PTC加热器的热学性能。

1 物理模型

空调PTC加热器由加热芯与散热片钎焊制作而成。现有空调PTC加热芯结构如图1所示：δ1=3 mm；δ2=0.05 mm；δ3=0.2 mm；δ4=0.1 mm；δ5=0.5 mm。现有空调PTC散热结构如图2所示：d0=2 mm；H0=12 mm；L0=650 mm；W0=16 mm；δ6=0.5 mm；δ7=0.2 mm。

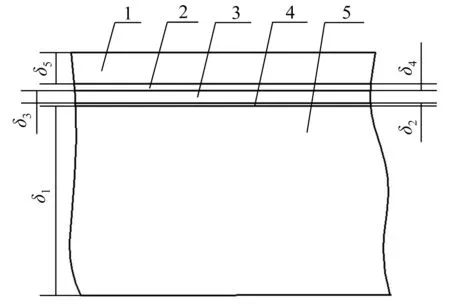
1—PTC陶瓷片；2—电极条；3—绝缘膜；4—铝外壳；5—胶水图1 PTC加热芯结构剖面图Fig.1 PTC heating core structure profile

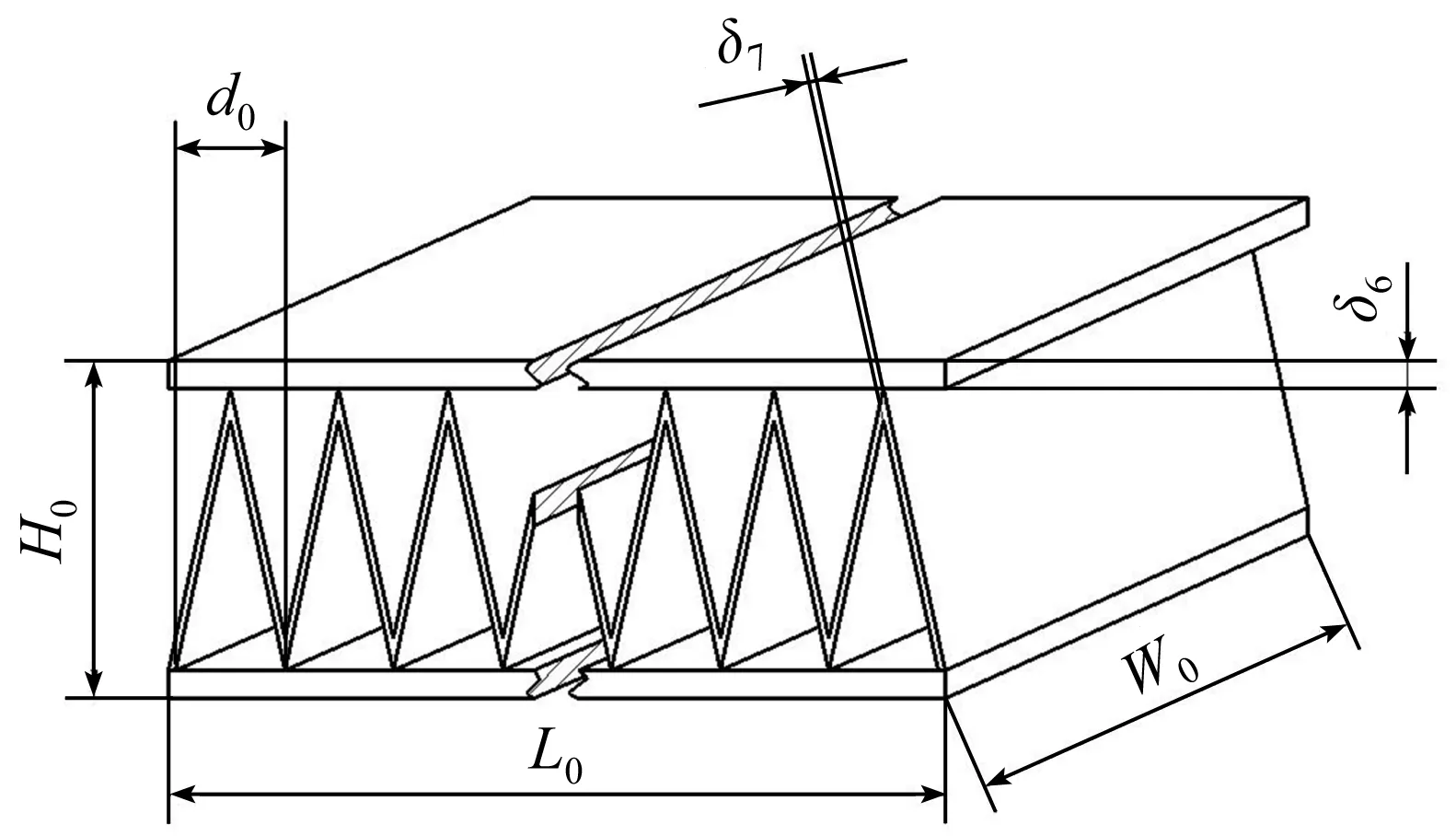
图2 PTC加热器散热结构Fig.2 Heat dissipation structure of PTC heater

2 理论分析

2.1 加热芯热分析

加热芯的整体发热速率和温度分布与单片PTC陶瓷片和各层材料的物性参数有关[7-9]。

假设同一片PTC陶瓷片达到稳态时，其表面温度均匀。则加热芯的导热问题可以看作一维导热问题。其温度分布示意图如图3所示，其结构示意图如图4所示。

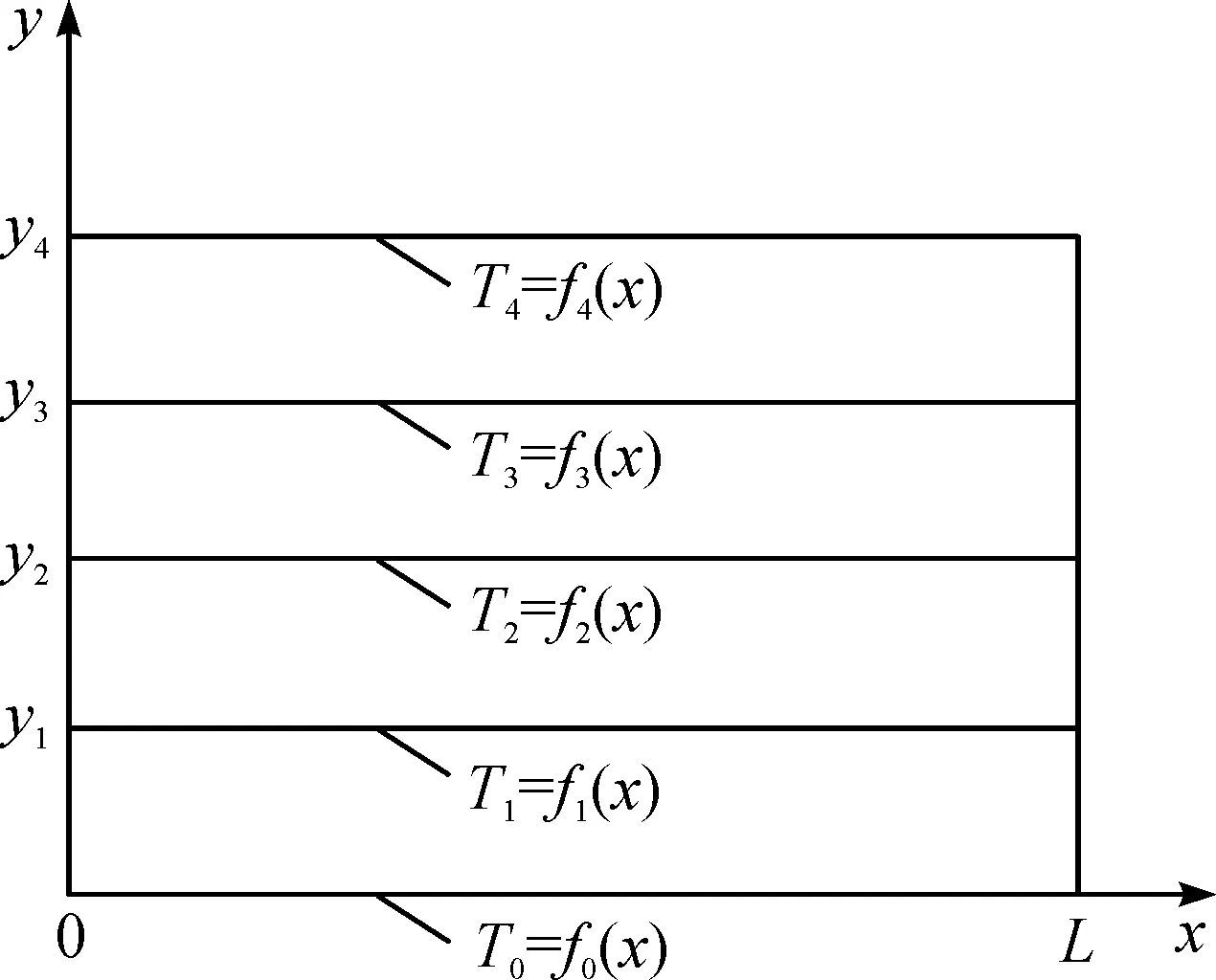
图3 加热芯温度分布示意图Fig.3 Schematic diagram of the temperature distribution of the heating core

图4 加热芯传热简化模型Fig.4 Simplified heat transfer model for heating core

热量的传递遵循傅里叶定律[10]为

(1)

式中：φ为热流量，指单位时间内通过某一截面的热量，稳态情况下φ=P额定=1 050 W；λ为导热系数，负号表示传热方向与温度梯度方向相反；A为垂直于传热方向的截面积。

由于模型关于x轴对称，对于y方向上的热传递，只研究y正半轴即可。设PTC片表面温度为T0，导热胶与电极条接触面温度为T1，电极条与绝缘膜接触面温度为T2，绝缘膜与铝外壳接触面温度为T3，铝外壳外表面温度为两侧接触面温度为T4，Ay=L0×W0=1.04×10-2m2。根据GB 50176—2005，PTC加热芯各层物性参数如表1所示。

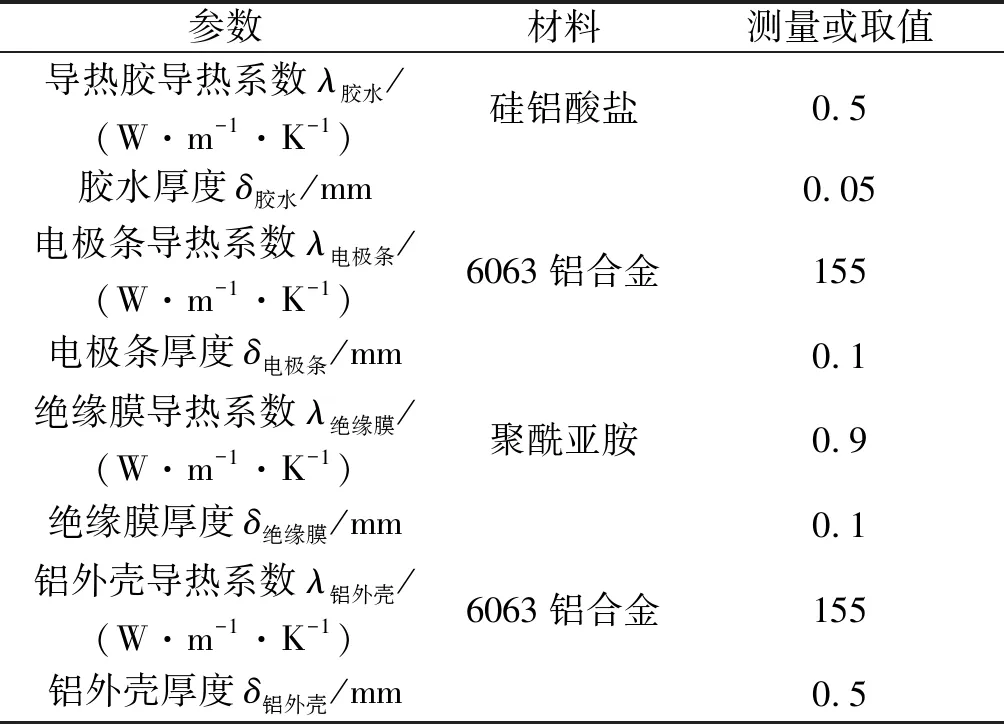
表1 PTC加热芯各层物性参数Table 1 Physical parameters of each layer of PTC heating core

各层材料热阻为

各层材料的温度差为

T0(x)-T1(x)=φ·Rhy胶水=10.08 K

T1(x)-T2(x)=φ·Rhy电极条=0.065 K

T3(x)-T2(x)=φ·Rhy绝缘膜=11.24 K

T3(x)-T4(x)=φ·Rhy铝外壳=0.33 K

可以看到仅考虑y方向上的传热，加热芯的表面温度为PTC片表面温度的一次函数。

同理仅考虑x方向的传热，计算两PTC片中点之间的热阻(δx=0.012 m)为

可以发现x方向上的热阻远远大于y方向，因此其对于温度分布的影响较小。

由于现有工艺的影响，对于同一批次PTC片其居里温度相同，达到稳态时其工作温度在居里温度的0～10 ℃内波动。PTC材料的物理特性如图5所示，图5各符号含义如表2所示。由图5可知：PTC材料工作温度会影响其工作电阻，从而影响其发热功率。因此不同的PTC片排列方式会影响加热芯的温度分布。PTC片的常温电阻和其工作电阻成比例关系，因此在固定选片的条件下，将功率较大的PTC片均布，可以使加热芯的温度分布更均匀，换热效果更好。利用Matlab，在固定PTC陶瓷片选片的条件下，以整体发热最优为目标对PTC陶瓷片进行优化排片。优化结果如表3所示。

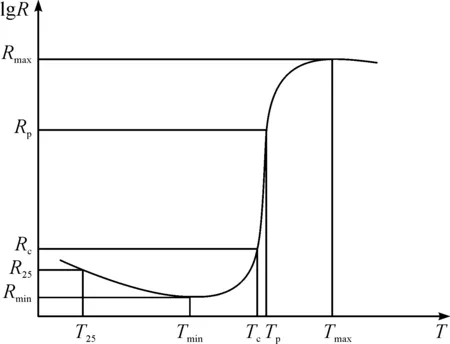
图5 材料温度电阻特性曲线Fig.5 Temperature resistance characteristic curve of material

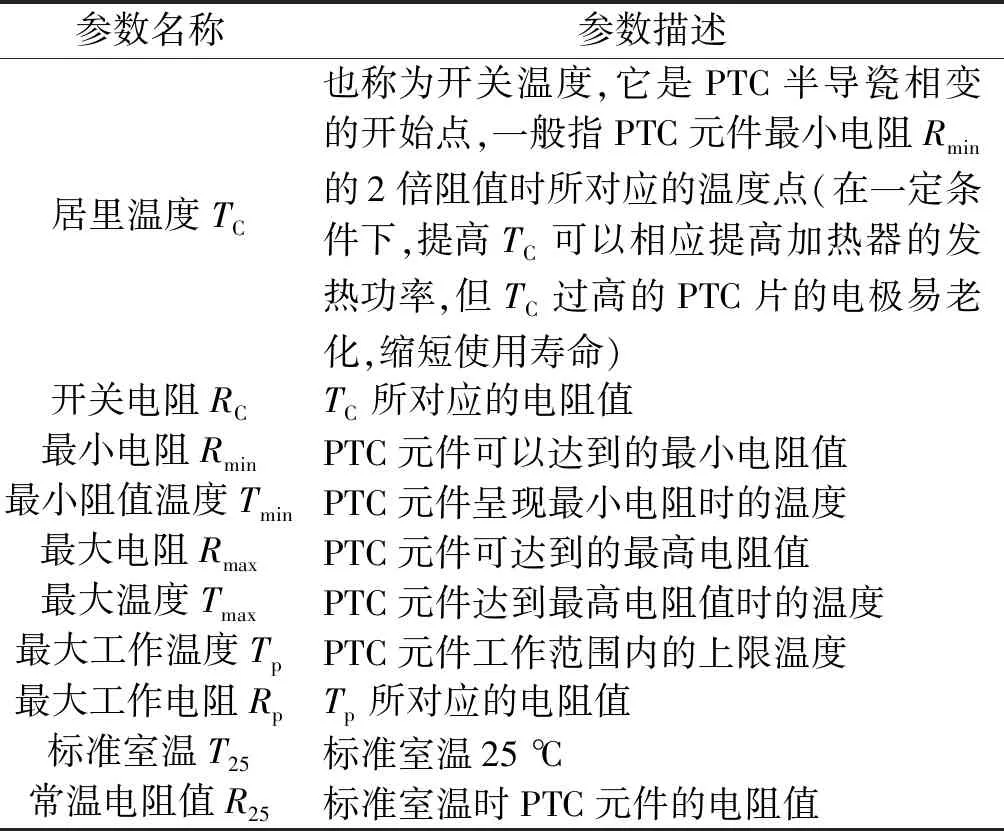
参数名称参数描述居里温度TC也称为开关温度,它是PTC半导瓷相变的开始点,一般指PTC元件最小电阻Rmin的2 倍阻值时所对应的温度点(在一定条件下,提高TC可以相应提高加热器的发热功率,但TC过高的PTC片的电极易老化,缩短使用寿命)开关电阻RCTC所对应的电阻值最小电阻RminPTC元件可以达到的最小电阻值最小阻值温度TminPTC元件呈现最小电阻时的温度最大电阻RmaxPTC元件可达到的最高电阻值最大温度TmaxPTC元件达到最高电阻值时的温度最大工作温度TpPTC元件工作范围内的上限温度最大工作电阻RpTp所对应的电阻值标准室温T25标准室温25 ℃常温电阻值R25标准室温时PTC元件的电阻值

表3 固定选片时整体发热的单目标最优排列

Table 3 Single objective optimal arrangement of overall heating for fixed selection

Ω

利用HT-02型红外热像仪测量达到稳态后的4 种排片方式和原有排片方式PTC加热芯的表面温度，结果如图6，7所示。

图6 测试设备Fig.6 Test equipment

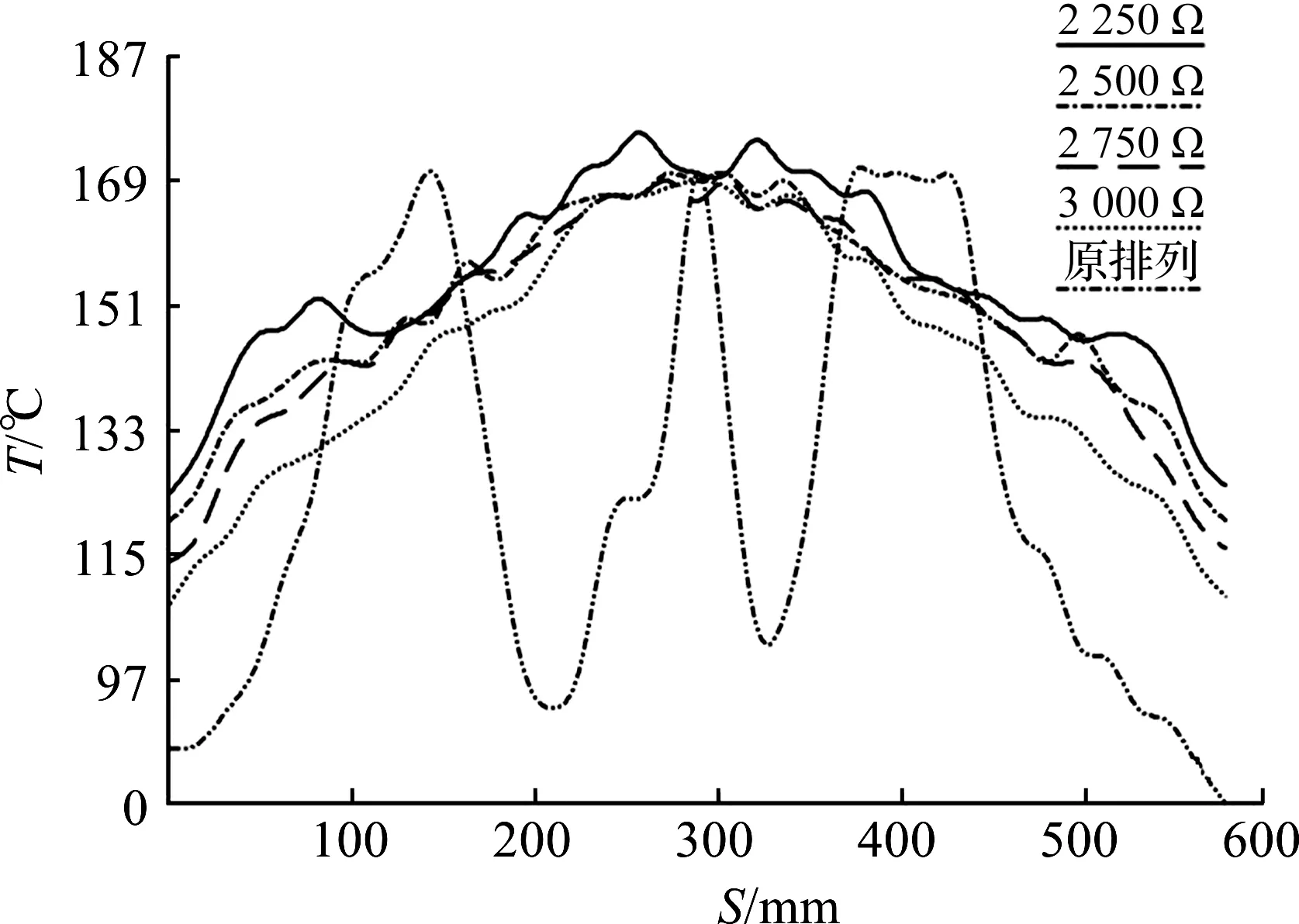
图7 5 种排片加热芯表面温度随位置变化曲线Fig.7 The change curve of the surface temperature of five kinds of platoon heating core

优化后加热芯的温度分布基本均匀。为方便后文计算优化，假设PTC加热芯表面温度分布均匀，其数值为真实温度分布的算数平均值，计算得T4=150.4 ℃。

2.2 散热片热分析

空调PTC加热器三角形散热翅片结构简图如图8所示。假设任意截面上温度均匀，根据导热微分方程[10]，可得三角形结构的热平衡方程为

(2)

对应的边界条件为

(3)

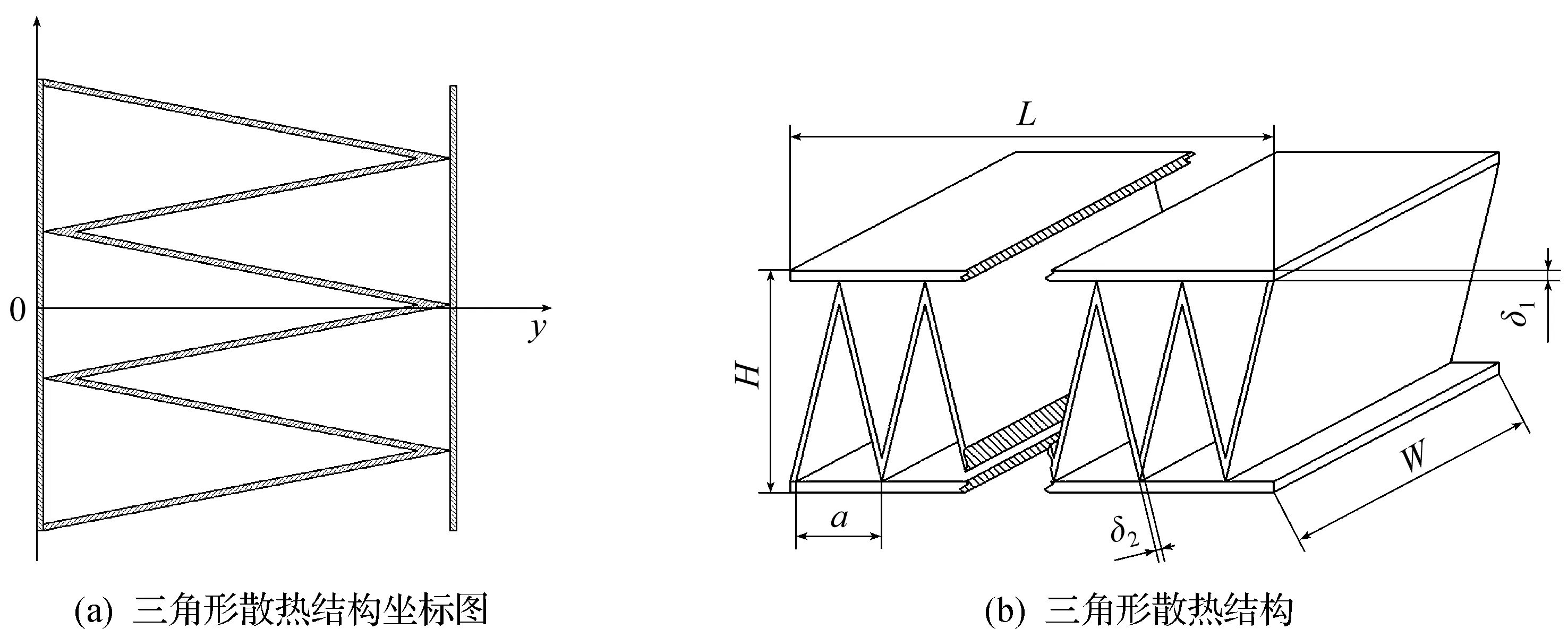
图8 三角形散热结构尺寸图Fig.8 Dimension diagram of triangular heat dissipating structure

式(2)为二阶线性齐次常微分方程，其通解为

θ=c1emx+c2e-mx

(4)

式中：c1，c2为两个常数。联结式(3，4)可得三角形散热片的温度分布为

(5)

(6)

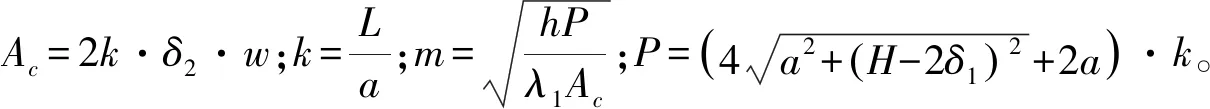
根据热阻[11-12]的定义

(7)

可以看出散热片热阻为a，h，W，δ2的关系式。在空调内，PTC加热器的空间尺寸(长方体)已定，因此变量仅有散热单元间距a与翅片厚度δ2，如图8所示。

以热阻最小为优化目标，采用Matlab求解。根据实际情况，给定范围(单位mm)为1≤a≤30,0.1≤δ2≤1，计算结果如图9，10所示。

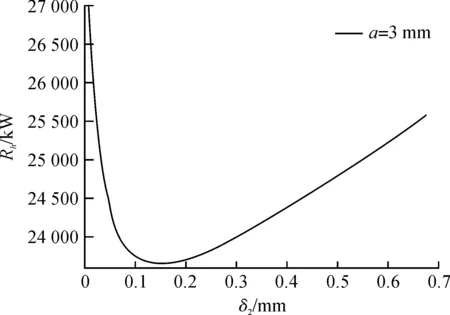
图9 δ2对Rh的影响Fig.9 The influence of δ2 on Rh

图9给出了在a=3 mm时，散热翅片热阻Rh与δ2的关系。从图9可以看出：Rh随δ2数值的增大先减小后增大；存在点δ2=0.154 mm使得Rh取得最小值Rh=2.324 3×104k/W。

图10 a对Rh的影响Fig.10 The influence of a on Rh

图10给出了在δ2=0.2 mm时，散热翅片热阻Rh与a的关系。从图10中可以看出：Rh随a数值增大而增大。但是考虑到PTC加热器力学性能的影响，a不能无限小，根据力学实验分析，取a=2.5 mm。

综合图9，10，得到三角形散热片最优尺寸：a=2.5 mm；δ2=0.154 mm，其散热片热阻Rh比现有产品降低了5.62%。

3 仿真验证

使用流体仿真软件COMSOL对散热片进行仿真求解。由于PTC加热器宽度较小，因此数学模型选用标准层流模型。实际PTC长650 mm，其结构由重复的三角形组合而成。如按实际尺寸比例进行建模，则三维模型巨大，这会导致处理网格划分时，计算模型的网格数量巨大，这不仅需要高性能的计算机，而且仿真计算的时间也会极长。因此为简化计算量，选取20 mm长的单元作为仿真模型，使用Solidworks进行3D建模，建立的模型如图11所示。使用COMSOL进行仿真之前必须对模型作出如下假设：1) 换热流道内的流体空气是不可压缩的牛顿流体；2) 忽略重力的影响；3) 流体的热物理性能，被认为与温度和压力无关；4) 除了空气流道与PTC加热器之间以及PTC加热器内部外，其他截面均没有热交换。

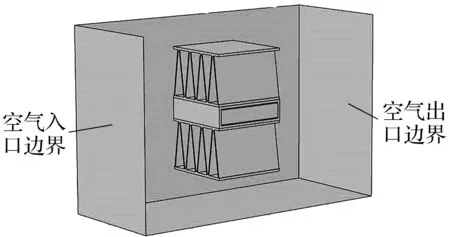
图11 PTC 20 mm单元边界图Fig.11 PTC 20 mm unit boundary graph

3.1 边界条件

如图11所示，根据实际情况，设置空气入口的边界条件：入口平均速度3 m/s，入口空气温度为295 K，空气的物性参数如表4所示。出口采用流出边界条件。因为流场出口的流动速度、温度和压力都是不确定的，因此设置能量仅从出口流出。根据实际情况在PTC加热器四周建立30 mm×40 mm×60 mm的空气流场，空气流场四周作绝热壁面设定，入口设置温度恒定为295 K，热量仅从出口流出。对于内部PTC加热器，由于仅截取20 mm长单元，因此图12中的a，b面也为绝热壁面设定，热源为PTC加热片，稳态下热源单位体积输出功率为4 154 kW/m3，其它内部各层材料包括导电导热胶、电极条、绝缘膜和铝外壳。电极条与铝外壳的材料为6063号铝合金，导电导热胶的材料为硅铝酸盐，绝缘膜的材料为聚酰亚胺。其物性参数如表5所示，其单元尺寸如图12所示。

表4 空气流体物性参数Table 4 Physical properties of air

图12 PTC 20 mm单元尺寸图Fig.12 PTC 20 mm unit size diagram

材料导热系数/(W·m-1·K-1)密度/(kg·m-3)恒压热容/(J·kg-1·K-1)PTC陶瓷600.02 7001006063铝合金880.02 700900硅铝酸盐0.51 300710聚酰亚胺0.69201 250

3.2 翅片单元间距对换热的影响

为了验证第2节公式的正确性，对三角形PTC加热器在δ2=0.2 mm不变的条件下，取a为1，1.5，2，2.5，3，3.5，4，4.5，5，5.5 mm，进行仿真验证。图13为PTC加热器流道内空气温度与PTC加热芯外表面的温度差与a的关系图。

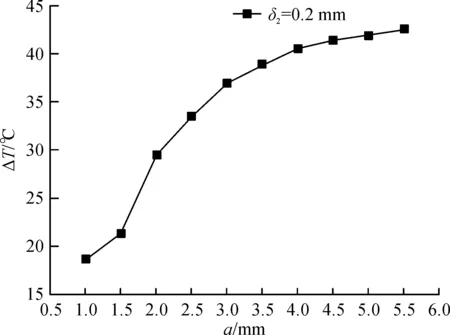
图13 平均温差与a关系图Fig.13 The relationship between average temperature difference and a

如图13所示，PTC加热器在δ2不变的条件下，流道内空气温度与PTC加热芯外表面的温度差随翅片单元间距增加而增加，增速逐渐减小。这是由于翅片单元间距变大，在总长度不变的前提下，换热面积减少。同时内部通道流入的空气增多，而流道内空气处于层流状态，空气为热的不良导体，只有边界层空气温度较高。流道内空气最大热边界层厚度为0.888 mm，即换热基本仅在距散热片表面0.888 mm的范围内发生。a在(1,1.5)范围内的斜率小于(1.5,2)。这是由于当翅片单元间距过小时，空气由于压降的问题，无法完全接触散热器表面，导致换热不完全。层流状态下的热边界层厚度计算[13-15]式为

(8)

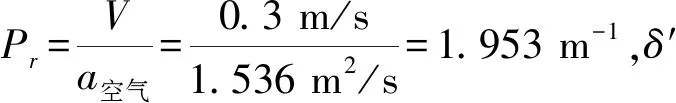
(9)

式中Rex为临界雷诺数，即

(10)

式中：u∞=10 m/s；xe=1.6×10-3m；v=15.06×10-6m2/s。

将式(9，10)带入式(8)，取x的最大值x=1.2×10-2m计算，得热边界层厚度最值为0.888 mm。

3.3 翅片厚度对换热的影响

同理对三角形结构PTC加热器在a=2.5 mm不变的条件下，取δ2为0.05，0.1，0.15，0.2，0.25，0.3，0.35，0.4，0.45，0.5 mm进行仿真。图14为PTC加热器流道内空气温度与PTC加热芯外表面的温度差与δ2的关系图。

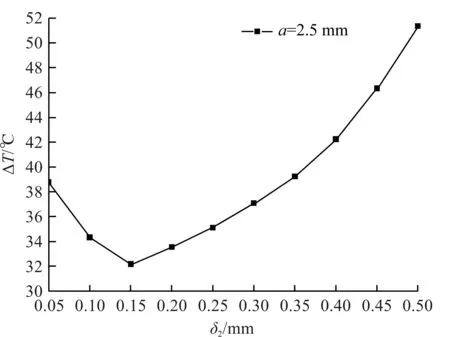
图14 平均温差与δ2关系图Fig.14 The relationship between average temperature difference and δ2

如图14所示，三角形PTC加热器在δ2不变的条件下，流道内空气温度与PTC加热芯外表面的温度差随翅片厚度增加，先减小后增加。这是由于随着翅片厚度增加，翅片内部的传热效果越好，温度在翅片表面的分布越均匀，对空气的加热效果越好。但PTC加热器总长不变的条件下，翅片厚度增大，翅片单位的总数量减小，换热面积减小，又导致换热效果降低。因此必然存在一个最佳翅片厚度δ0使得换热效果最优。

4 实验验证

4.1 实验原理

当加热器工作至稳态时，其热源温度维持不变。其传递至周围环境的热量等于其自身转化电能产生的热量。假设PTC加热器产生的热量只能通过热对流与热辐射两种方式传递释放到周围环境中，则通过测量内部热源的生成量就可以获得其向周围环境散发的热量。内部的热源为PTC陶瓷片，其原理与电阻加热一致，因此通过测量PTC陶瓷片两端的通电电压、电流和通电时间就能计算获得内热源发热量。将一个测试周期的发热热量与测量时长相除即可得到翅片的散热功率。实验装置[16-17]如图15所示。

实验装置安装于1 m3的实木密封容器中。空气通过横流风机流过PTC加热器，通过风速传感器与风速控制模块，将风速控制在3 m/s。PTC加热器正前方0.6 m处的平面均匀分布9 个温度传感器。温度传感器以1 次/s的速度记录温度。当9 个温度传感器的温度10 s温度变化幅度小于0.05 ℃时，结束实验。

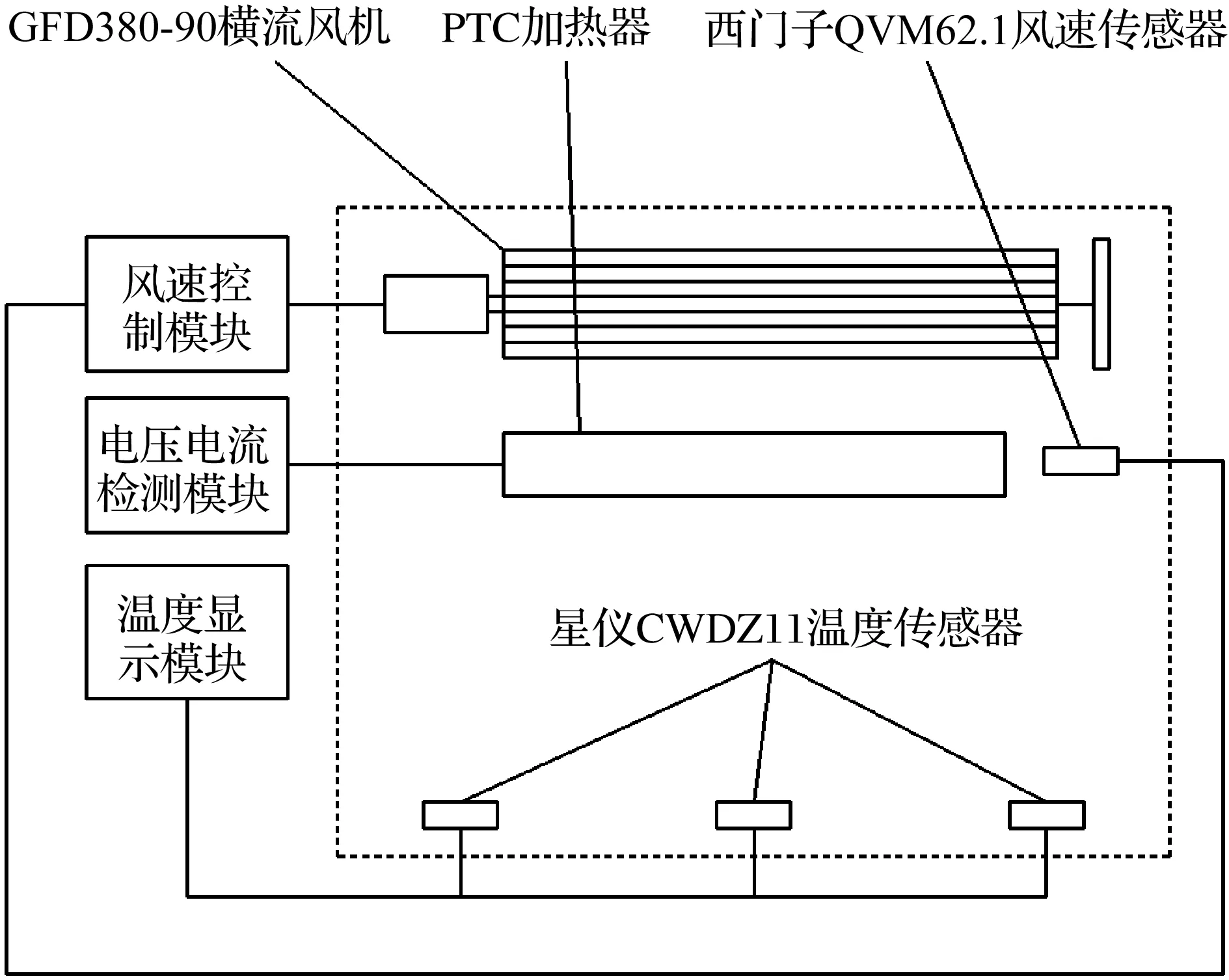
图15 实验装置原理图Fig.15 Schematic diagram of experimental device

实验材料选取为奥克斯空调用PTC加热器，与改装PTC加热器。其中改装PTC加热器为以奥克斯空调用PTC加热器为原型，将散热翅片拆除，并重新钎焊上优化结构翅片。三角形翅片厚度为0.15 mm，材料为6063铝合金条，加工后三角形单元间距为0.25 mm。

4.2 实验数据及分析

由图16，17可以看出：优化PTC加热器0～20 s内加热速度略慢于原有PTC加热器，但20～40 s加热速率增速更快。达到稳态后其空气温度也相对更高。由图18可以看出：0～10 s内，两种PTC加热器的加热功率基本一致，10 s以后直到稳态，优化PTC加热器加热功率均大于原有PTC加热器。两种加热器都在60 s左右达到稳态。结合表6的数据可以看出：优化结构的PTC加热器，由于散热片厚度减小，间距减小，材料消耗增加，因此初始时消耗更多能量使自身温度升高，而两种散热器0～10 s内的的加热功率基本一致，因此优化PTC加热器对温度的初始加热速率偏低。当PTC加热器本身温度较高时，优化PTC加热器由于换热面积更大，对空气的加热速率提高的更快。又由于PTC材料特性，其发热功率与环境因素有关，散热环境越好，其发热功率越大。因此优化PTC加热器达到稳态时加热的空气温度高于原有PTC加热器，这说明优化翅片结构的换热性能更好。

图17 原有结构与优化结构加热温度变化速率与时间关系图Fig.17 Relationship diagram of temperature change rate and time between original structure and optimized structure

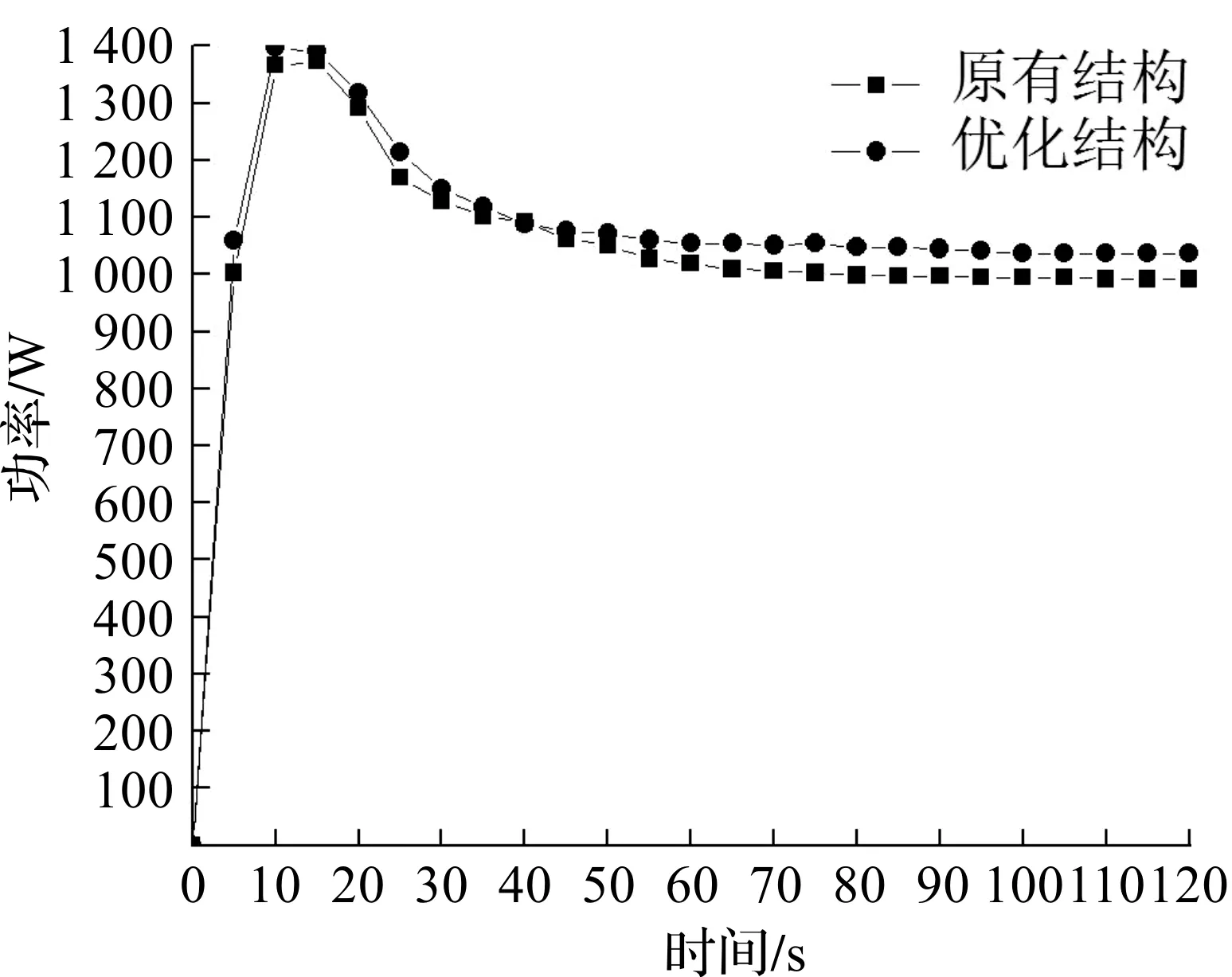
图18 原有结构与优化结构加热功率与时间关系图Fig.18 The relation diagram of the heating power and time of the original structure and the optimized structure

5 结 论

对空调PTC加热器的整体结构进行了热分析，结论如下：1) PTC片的排布对PTC加热器的加热芯表面的温度分布起绝对性作用，将发热功率大的PTC片均布可以使加热芯表面温度基本均匀。2) 以热阻最小为优化目标，得到空调PTC加热器优化结构为a=2.5 mm，δ2=0.154 mm。优化结构的热阻比原有结构减小5.62%，实验证明优化结构换热性能更优。