一类最优局部修复码的构造

蒋静 王金玉

摘   要：有多个互不相交修复集合的局部修复码是一类很重要的能应用于提高分布式存储系统修复效率的码。本文利用多种组合结构，如填充、平衡不完全区组设计等，构造了参数较小的最优局部修复码，其中每一个修复集合至多包含4个元素且恰有一个是校验元。

关键词：局部修复码  分布式存储系统  填充  平衡不完全区组设计

中图分类号：TN911                                 文献标识码：A                       文章編号：1674-098X（2019）02（a）-0088-05

在大数据环境下，分布式存储系统被应用于海量数据的存储。在分布式存储系统中，原始数据被分成k个等大小的片段，然后被编码成n个片段存储在n个不同的节点中，使得当要修复1个节点时，我们只需连接其中部分节点。根据实际需求选用特定的编码是分布式存储的一项关键技术，其中用到的局部修复码是近几年非常热门的一个研究方向。最近，Cai等[1]在假设每个节点有多个修复集合，且每一个修复集合只包含一个校验元的前提下，利用组合结构填充（packing）构造了一些最优局部修复码的无穷类。本文基于文献[1]的结果，利用多种组合结构构造了若干最优局部修复码。

1  相关概念

1.1 局部修复码

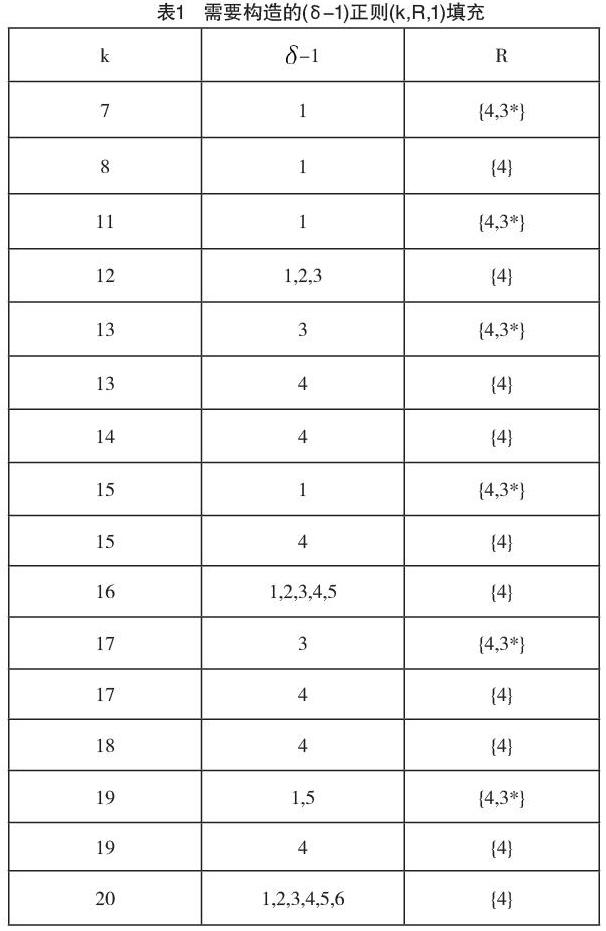
定理1的证明：由推论1-4和引理7-8可知，存在一个（δ-1）-正则（k，R，1）-填充，其中（k，δ-1，R）的值为表1中列出的值。由引理1可知，存在一个拥有局部信息（r，δ，1）c的最优对称码。

2  结语

本文基于文献[1]的结果，构造了当k（δ-1）≡0，3（mod 4）且k≤20时，拥有局部信息（4，δ，1）c的最优对称码。本文方法也可以用于构造k>21时的最优局部修复码，但这样的局部修复码结构较复杂、相应的构造也更加困难，需要对构造方法做进一步地改进。

参考文献

[1] Cai H， Cheng M， Fan C， et al. Optimal Locally Repairable Systematic Codes Based on Packings[J]. IEEE Transactions on Communications， 2019， 67（1）： 39-49.

[2] Huang C， Chen M， Li J. Pyramid Codes： Flexible Schemes to Trade Space for Access Efficiency in Reliable Data Storage Systems[J]. ACM Transactions on Storage， 2013， 9（1）：3.

[3] Wang A， Zhang Z. Repair Locality with Multiple Erasure Tolerance[J]. IEEE Transactions on Information Theory， 2014， 60（11）： 6979-6987.

[4] Rawat A S， Papailopoulos D S， Dimakis A G， et al.  Locality and Availability in Distributed Storage[J]. IEEE Transactions on Information Theory， 2016， 62（8）： 4481-4493.

[5] Chung H， Kumar P V. Optical Orthogonal Codes-New Bounds and an Optimal Construction [J]. IEEE Transactions on Information Theory，  1990， 36（4）： 866-873.

[6] Yin J. Some Combinatorial Constructions for Optical Orthogonal Codes[J]. Discrete Mathematics， 1998， 185（1-3）： 201-219.

[7] Colbourn C J，   Dinitz J H. Handbook of Combinatorial Designs[M]， Chapman & Hall/CRC， vol. 42， 2006.