基于改进树种算法的模糊聚类图像分割*

肖石林宣士斌温金玉

(广西民族大学 信息科学与工程学院，广西 南宁 530006)

0 引言

随着科学技术的飞速发展，越来越庞大的信息数据量需要处理.其中图像在信息数据处理过程中有着最直观，信息量宽广的特点，图像信息在人类日常生活中接触极多.但是面对庞大的图像信息源，可能只有某一块区域是人类所需要的，这就要求人类利用相关的图像处理算法将一些区域分割开来以便后续图像研究.将一幅完整的图像划分为多个有意义的目标区域的这类方法便被称作为图像分割.[1]一些常见的图像分割算法有如下几种：(1)阈值化分割[2]是图像分割算法中较早出现的算法，在阈值分割算法中，难点和关键是阈值的选择.阈值化分割算法的各种变形算法都是基于阈值的选取衍变而来.其中直方图方法、最大类间方差法、最大熵方法等在阈值化图像分割中广泛应用.(2)基于区域的方法[3]假如在一个相邻区域的像素在计算机视觉上有一些比较相似的特征，比如有灰度特征、纹理特征等.这种方法它主要是利用了图像空间信息，那么所分割的图像也是连续不间断的，并且它不受图像中分支数的约束，其中区域增长，区域分割和区域合并算法在区域分割图像方法中经常被使用到.(3)在图像分割领域中，聚类的分割算法主要分为硬聚类和软聚类.软聚类是模糊C-均值聚类算法(FCM)，[4]它在图像分割领域的研究一直都是热门，本文所要用的方法便是通过不停迭代隶属度矩阵和簇中心以得到目标函数最小值的模糊C-均值聚类(FCM)算法.

除此之外，最近几年元启发式算法[5]发展迅速，在国际学术界掀起了一种新的研究热潮，引起了许多学者的高度关注.与一些传统的优化算法相互比较，元启发式算法在解决复杂可以更直观、更有效地解决复杂的实际问题.它们的过程通常是先创建一组随机解，然后使用设定的更新规则来优化这组解，最后获得最优解.元启发式算法是基于社会行为[6]和自然现象[7]产生的.比如，遗传算法(GA)[8]是一种基于达尔文生物进化理论的算法，最关键的搜索最优解的过程是模拟生物进化的过程.粒子群优化(PSO)[9]是基于对鸟的社会行为和个体行为的研究，它要求候选解围绕当前个体的最优位置和当前种群的最佳位置进行移动.重力搜索算法(GSA)[10]是一种基于万有引力定律和牛顿第二定律的所衍变出的种群优化算法，它依赖于个体之间的引力相互作用去寻找最优解.灰狼优化算法(GWO)[11]是一种基于对灰狼捕食行为和等级制度的算法，优化的目的是通过灰狼寻找猎物、包围猎物、捕食猎物和攻击猎物的过程来实现的.2015年，Mustafa Servet Kiran等人提出了一种新的叫作树种优化(TSA)[12]的元启发式算法.在众多的元启发式算法中，树种算法寻优能力较GA、PSO等一些经典传统优化算法更强，从而受到了学术界的广泛关注.它是通过模拟自然界中树木的繁殖方式来实现最优函数值的寻找.首先在解空间内随机生产一批树木，即一批解，然后在这一批树木中挑出生产种子能力最强的一批解.这一批可行解便会接着随机地产生新生种子，这些种子的生成方式有两种：一种迭代方式侧重全局搜索，另一种则是局部搜索，搜索趋势常数ST决定着他们的迭代生成方式.最后，这些新产生的种子进行再次寻优迭代，直到产生一个最优秀的解.

本文在标准树种算法(TSA)的基础上提出改进树种优化算法(ITSA)，将判断参数ST由固定值转变成随迭代次数逐渐增大的变量，并将步长因子构造非线性递减函数，用以提高本文中TSA算法收敛的精度和速度，经过这样的调整后，使得TSA算法迭代初期侧重点是全局搜索而在算法后期侧重点是局部搜索，来解决模糊聚类中对初始聚类中心的求解过程中计算复杂，易陷于局部最优等问题.本文的后续部分是按如下方式进行的，第2部分介绍树种算法及改进树种算法并对其进行算法测试.第3部分给出实验结果和数据分析.最后，第4部分进行论文总结.

1 树种算法

1.1 标准树种算法

树种算法模拟自然界中树木生成种子的衍变特点，从而被提出来成为一种新兴元启发式搜索算法，经过初步的研究结果表明，该算法的寻优能力优异，有希望超过当前诸如PSO(粒子群算法)、[13]ABC(人工蜂群算法)、[14]FA(萤火虫算法)[15]等群体智能算法，该算法模拟大树的繁殖方式来实现最优值的寻找.首先在解空间内随机生产一批树木，即一批解，然后在这一批树木中挑出生产种子能力最强的一批树木.这一批可行解便会接着随机地产生新生种子，这些种子的生成方式有两种：一种迭代方式侧重全局搜索，另一种则是局部搜索，搜索趋势常数ST决定着他们的迭代生成方式.最后，这些新产生的种子进行再次寻优迭代，直到产生一个最优秀的解.

在树种算法开始搜索时，利用式子(1)来随机初始化树木的位置，为优化问题产生可行解：

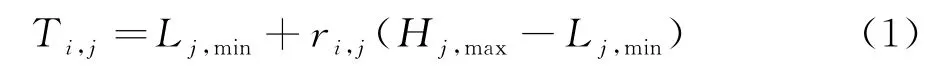
式中L j，min是搜索空间的下界，H j，max是搜索空间的上界，r i，j是在每一维空间和位置上的一个随机数，r i，j∈ (0，1).

并不是所有的树产生种子的能力都是一样的，根据测试表明，10%树的种群数量产生的种子数量最低，25%树的种群数产生的种子数量最高.所以生成了树木之后，我们要对种群进行优化，利用式(2)选出最好位置的树木：

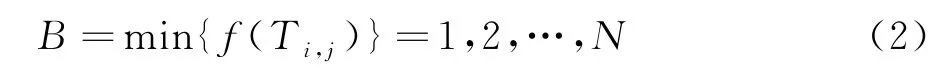
式中N是树木的种群数量.

在搜索解空间中生成了最好位置的树木后，这一批树木便会接着随机地产生新生种子，这些种子的生成方式有两种：一种迭代方式侧重全局搜索，另一种则是局部搜索，搜索趋势常数ST决定着他们的迭代生成方式：

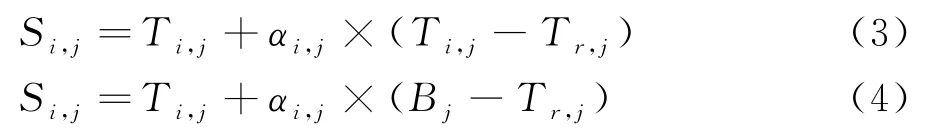
其中S i，j是第i棵树上产生的第i颗种子的第j个元素，T i，j是第i棵树上的第j个元素，B j是当前位置最好的树上的第j个元素，T r，j是可行解中随机生成的第r棵树上的第j个元素，αi，j是进行迭代的步长因子，是一个随机数，αi，j∈ (-1，1).

1.2 改进树种算法

在标准的树种算法中，搜索趋势常数ST通常为固定值，但是这个参数ST在树种算法中又是一个很重要的参数，在算法迭代的过程中，如果ST一直较小，虽然它会加速算法的收敛，并且会有利于其全局优化，但它可能无法获得更高精度的最优解.反之，如果ST一直较大，算法又会一直进行局部寻优，导致算法的时间复杂度明显提高.步长因子αi，j其大小和方向都是高度随机的，这有益于进行全局寻优，很快就可以接近全局最优解，但随着TSA算法在进行了多次迭代运算后，后期的局部寻优过程会因步长因子跳跃性太强而得不到较精确的局部最优解，从而导致后期收敛速率变慢.

通过对布谷鸟算法[16-17]和粒子群算法[18]以及其他智能算法的研究，本文针对树种算法中搜索趋势常数ST构造了非线性递增函数，以及对步长因子αi，j构造了非线性递减函数：

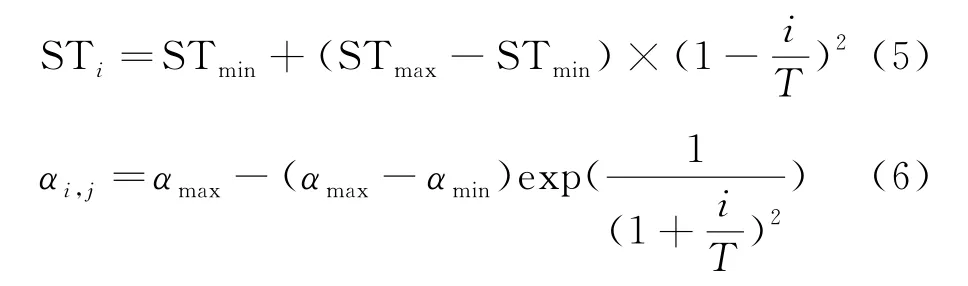
其中，STmax和STmin为搜索趋势常数ST的最大值和最小值，αmax和αmin为步长因子αi，j的最大值和最小值，i和T分别表示当前迭代次数和最大迭代次数，采用上面两式，可以提高算法的收敛速度和精度，随着算法的动态变化而调整步长因子和搜索趋势常数，改进后的树种算法(ITSA算法)迭代初期更倾向于全局寻优，而迭代后期利用全局最优解进行局部寻优.

ITSA算法的主要步骤如下：

步骤1 设置种群数N，搜索趋势常数的最大值STmax和最小值STmin，步长因子的最大值αmax和最小值αmin，问题维数D，用式子(1)生成一些随机树，为优化问题挑选适应度函数，再利用式子(2)在这些随机树中选择最优解.

步骤2 利用位置较优的树木生成种子完成迭代过程，此过程中利用式子(3)和式子(4)对这些位置较优的树进行选择迭代，若rand＞STi，则用式子(3)进行全局寻优，若rand＜STi，则用式子(4)进行局部寻优.

步骤3 选出最优解，并保留上一代最佳树木位置，若生成的种子比上一代树木位置更优，则用新生成树木的位置替代当前位置.

步骤4 迭代过程中迭代次数少于最大迭代次数，则返回步骤2，否则迭代结束，输出全局最优目标函数值.

1.3 性能比较

为了评价ITSA的有效性，我们从文献[19-22]中选取了几个测试函数，设置其维数等于50，因为高维测试函数可以反映出算法的优越性.

表1 测试函数Tab.1 Test function

本文选取了主流算法中的5种算法来和ITSA作比较，它们分别是ABC，[14]GSA，[10]PSO，[9]GWO，[11]TSA.[12]各算法的参数设置如下：

实验的每一步都是在 Windows 7 Intel Core i5，4G RAM环境下Matlab平台上进行的.为了突出比较的公平性，每种算法分别在测试函数中独立运行30次，并在最好值、最差值、平均值和标准差4个方面进行比较.最好值、最差值、平均值和标准差的表示分别用Best、Worst、Mean和Std来替代.排名的顺序是以Std为标准.

从表2来看，针对单峰测试函数Sphere本文提出的ITSA算法实验结果远优于其他算法测试结果，但是从函数Resonbrock来说和灰狼算法测试结果相差不大.针对多峰测试函数Griewan来说，实验结果排名第二，仅次于灰狼算法.但在其他两个多峰测试函数上来看，本文提出的ITSA算法的实验结果都是最优的.

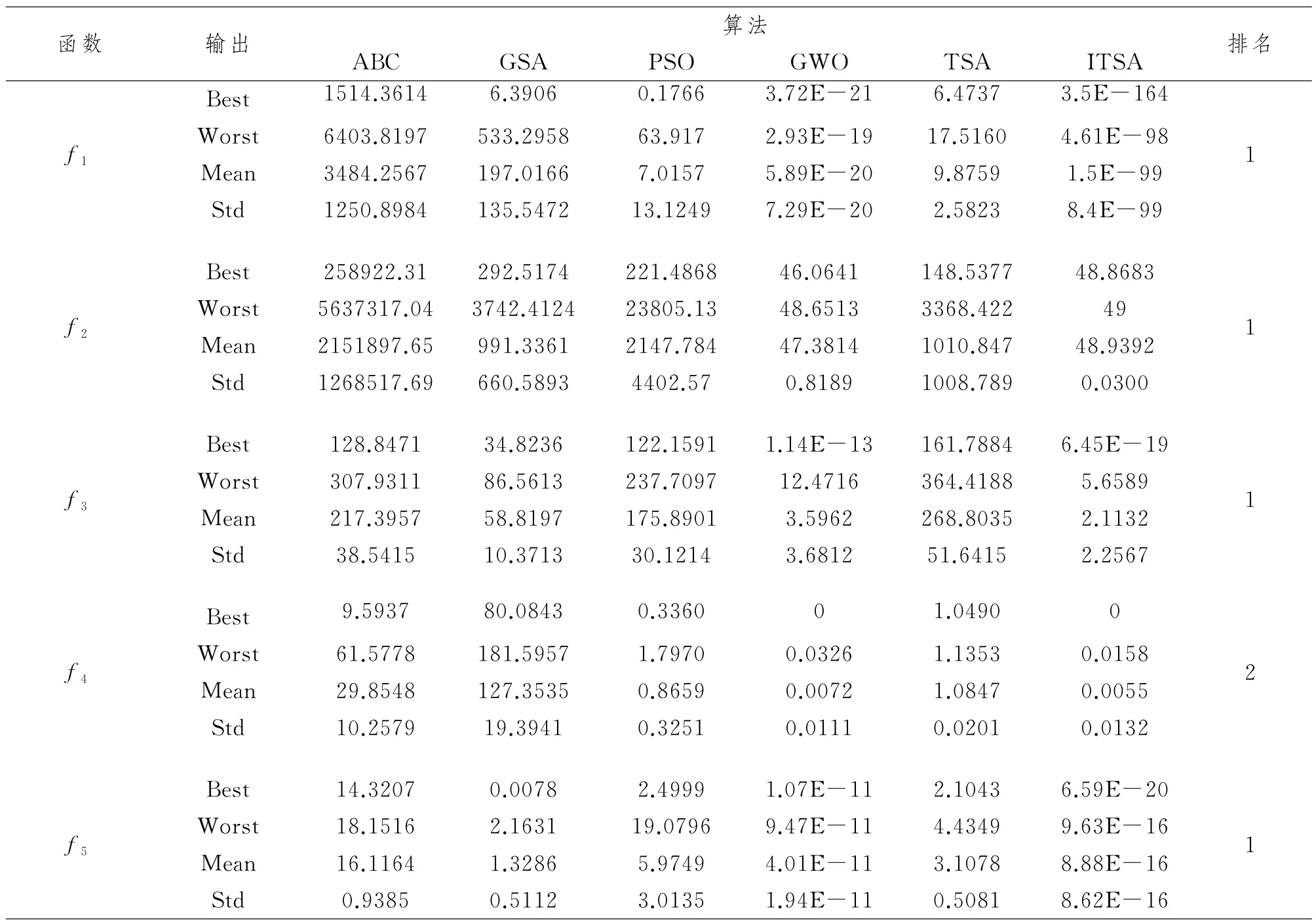
表2 测试函数结果比较Tab.2 Comparison of test function results

2 改进树种算法与模糊聚类图像分割(ITSA_FCM)

2.1 FCM算法介绍

模糊C-均值聚类(FCM)算法是通过不停迭代隶属度矩阵和簇中心以得到目标函数最小值的过程，在进行图像分割的时候它是根据像素以及聚类中心的加权相似性对目标函数不断的进行迭代优化以便寻找最优解.设有n个数据样本为X={x1，x2，…，x n}，c(2≤c≤n)是要将数据样本分成的类别的数目，A={A1，A2，…，A C}表示相应的c个类别，U是相似度矩阵，各类别的聚类中心为{v1，v2，…，v c}.根据以上定义，FCM的目标函数为：

通过对式(1)引入拉格朗日乘子，更新隶属度矩阵和聚类中心：

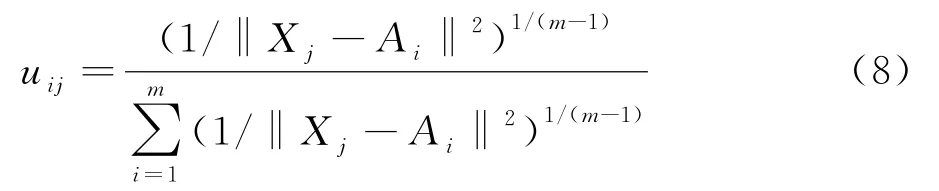
其中，u ij表示第i个样本点属于第j类的隶属度，u ij∈ [0，1].

FCM算法的主要步骤如下：

步骤1 确定初始的聚类类别数c和模糊指数b，定义条件终止参数ε，以及初始化隶属度矩阵U.

步骤2 通过式(2)和式(3)更新每次迭代后的隶属度矩阵U和聚类中心A的值.

步骤3 如果‖U(t)-U(t-1)‖＜ε，则此算法结束，如果没有大于条件终止参数所定义的值，则返回步骤2，继续完成迭代过程.

FCM算法在图像分割领域虽广泛应用但还存在一些问题，它很难选取算法初始迭代中心，而且在迭代后期容易陷入局部最优解.

2.2 改进树种模糊聚类算法

改进的树种优化算法能有效优化FCM容易陷入局部最优值的问题，还能克服原始树种算法迭代寻优随机性等问题.将改进的树种优化算法和FCM相结合用于图像分割不仅可以有效提高算法效率，加快最优解求解的同时，还能取得不错的图像分割效果.

评价每颗种子的生成价值，定义适应度函数：

其中，n为常数;J(U，A)为区域图像中每个像素点的目标函数值之和，它的值越小，代表聚类效果越优异.因此，要想聚类效果好，则适应度函数f的值越大.种子的位置就是由每次迭代产生的聚类中心位置来更新，最终迭代结果的最优解就是最优树种位置，也是最后的聚类中心.

改进树种算法的模糊聚类图像分割流程如下：

步骤1 参数初始化.包括树木种群规模定义为N，搜索维度定义为D，搜索趋势常数ST设置最小值STmin和最大值STmax.算法的最大迭代次数定义为T，聚类中心类别数目定义为c，模糊指数定义为b等.

步骤2 对c个聚类中心进行随机初始化，即初始化最原始树木的位置，随机生成一批树.

步骤3 通过式(10)计算原始树木适应度函数值，从而选出较优位置的树木.

步骤4 根据式(3)或式(4)用种子更新上一代的树木位置，得到新树木的适应度函数值.

步骤5 将计算得到的新树木适应度函数值与上代比较，若较好则更新树木位置，否则不变.

步骤6 判断算法迭代次数是否大于算法终止阈值，若到达算法终止阈值，则输出最优树木位置，否则返回步骤4继续进行算法迭代.

步骤7 得到最优树种位置，即最终聚类中心后，根据式(8)和式(9)分别计算隶属度矩阵和聚类中心，输出分割结果.

3 实验结果和分析

本文将ITSA_FCM算法和PSO_FCM[23]算法对图像分割结果进行比较分析.在参数设置方面，聚类类别数设置为8，最大迭代次数设为50，STmax=0.5，STmin=0.1.在ITSA_FCM中，搜索趋势常数ST异常重要，它决定着迭代的进行方式，是进行全局寻优还是局部寻优.在算法迭代前期，ST取较小值，容易进行全局寻优，随着算法越来越接近全局最优解，ST值也趋向最大值，方便进行局部寻优.为验证算法的分割效果，本文在 Windows 7 Intel Core i5，4G RAM环境下Matlab平台上采用三个公开的标准测试图像Lena、Cameraman、Orangutan，以式子(10)为实验的适应度函数.

根据本文方法进行实验，待分割原始图像如图1(a)，(b)，(c)所示，图(2)及图(3)图(4)中(a)，(b)，(c)，(d)分别表示使用 FCM、PSO_FCM、TSA_FCM、ITSA_FCM这3种分割算法所得到的分割结果.从分割结果上看，原始FCM方法均出现了一些过分割的现象，分割效果不如后三者理想，而PSO_FCM方法与TSA_FCM分割方法在效果上差异不大，都比原始FCM方法更优且都比本文提出的ITSA_FCM效果差一点.例如，图(2)Lena用ITSA_FCM方法分割之后，头发和面部细节更清晰，图(4)Orangutan的眼部分割效果更好，轮廓更明显.接下来比较分割效率，计算以上几种算法的平均计算用时，分割效率结果见表3，从表3可以看出来，和FCM，PSO_FCM及TSA_FCM分割方法相比较，本文所提出的ITSA_FCM寻优方法可以更快地找到初始聚类中心，完成图像分割.

图1 原始图像Fig.1 Original image

图2 Lena分割结果Fig.2 Split results of Lena

图3 Cameraman分割结果Fig.3 Split results of Cameraman

图4 Orangutan分割结果Fig.4 Split results of Orangutan

表3 计算效率比较Tab.3 Computational efficiency comparison

4 结语

本文在标准树种算法(TSA)的基础上提出改进的树种优化算法(ITSA)，将判断参数ST由固定值转变成随迭代次数逐渐增大的变量，并将步长因子构造一个非线性递减函数，用以提高本文中TSA算法收敛的精度和速度，经过如此调整后，使得TSA算法迭代初期侧重点是全局搜索而在算法后期侧重点是局部搜索.针对传统的FCM容易陷入局部最优值和其初始聚类中心计算复杂等这些缺点，将改进的树种优化算法引入到FCM中.通过实验表明，ITSA_FCM算法不仅在图像分割效果上优于传统FCM，在算法运行时间上也明显优于传统FCM.