α-混合误差下非参数回归函数加权核估计的相合性*

李春雨

(广西师范大学 数学与统计学院，广西 桂林 541004)

0 引言

定义[2]：称随机变量{X n}为α-混合的，若存在非增的正数列，对存在)，其中，为所产生的σ-域.又若存在，则称{X n}是几何α-混合的.

设y1，y2，…，y n是固定在点x1，x2，…，x n的n个观察值，适合模型

其中，g(x)是[0，1]上的未知函数，且把g(x)在[0，1]外的值定义为0，{εi}是随机误差序列，且假定0=x0≤x1≤…≤x n-1≤x n=1.

Priestley和Chao[3]对未知函数g(x)提出了一种加权核估计

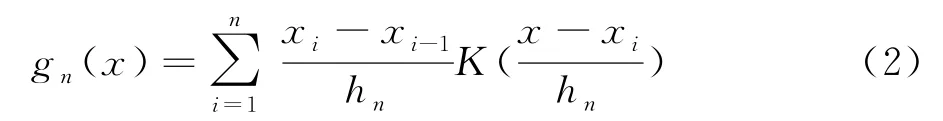
其中K(u)是Borel可测函数，且0＜h n→0(n→∞);Benedeti.J.k[4]在独立误差情形证明了g n(x)→g(x)，a.s;秦永松[5]在独立误差情形减弱了文[4]的条件下，证明了g n(x)的强相合性;杨善朝在φ-混合误差 、[6]NA相依下[7]研究了g n(x)的强相合性，获得了一些较弱的充分条件;李乃医[7]在混合误差情形，给出g n(x)了的强相合性和矩相合性的充分条件;于德明[1]在误差为α-混合条件下，要求，证明了g n(x)→g(x)，a.s.本文在α-混合情形下，减轻了对随机误差项的要求，在条件下研究了g n(x)的强相合性.

1 主要结论

基本条件：a)K(·)在R1上满足s阶Lipschitz条件，且在R1上有界;

b)g(·)在[0，1]上满足t阶Lipschitz条件.

定理1设满足a)、b)两个条件，且

1){εi}为α-混合，，存在常数r≥2，使;

2)存在常数θ＞r-1，

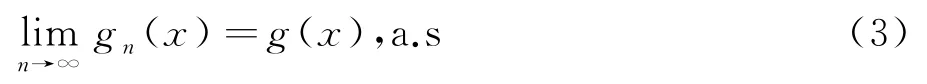
注：1)减弱了对K(·)的要求.本文对K(·)的要求在R1上满足s阶Lipschitz条件，K(·)连续且，从而K(·)有界.文[1]除了满足定理所需条件，还作以下要求：，.

2)对h n=n-1中的l降低了要求.文献[1]中要求，显然文献[1]对l的要求强于本文定理要求的.

3)放宽了对误差{εi}的条件.文[1]中要求{εi}为同分布几何α-混合，Eεi=0，又存在b i≥0，使

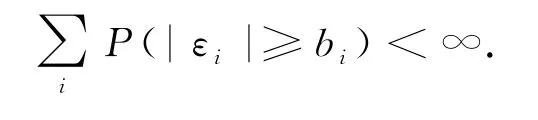
2 定理的证明

为了证明本文的主要结果，我们需要下述引理.

引理1[9]设{X n，n≥1}是α-混合序列，，那么

由式(1)和(2)有：

先证K n→0，由，

结合引理1知

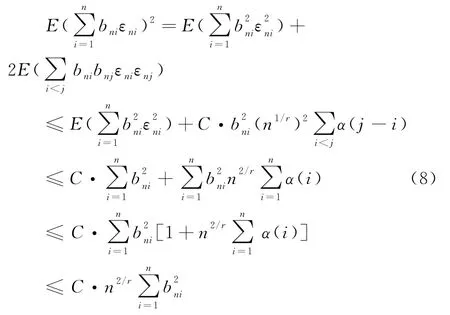
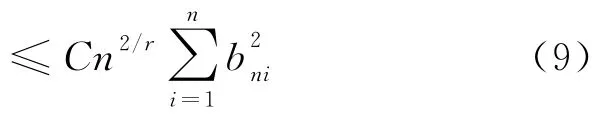
所以，对 ∀ε＞0有

而θ＞r-1，当n→ ∞ 时，.

由Borel-Cantelli引理可得，K n→0，a.s.

由(10)和(11)知，只需证

即证明

对∀ε＞0，由Markov不等式，当m≥n→ ∞时，由时有，

因此{S n，n≥1}是Cauchy序列，存在S，使得.

从而存在子序列{S nk}，使得S nk→S，a.s.

再由推广的Kolmogrov不等式得到：

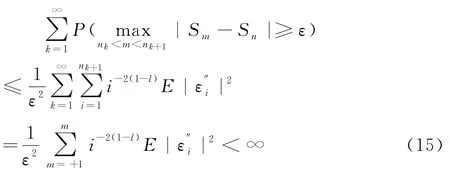
由Borel-Cantelli引理有，当k→∞时，

也就是得到S n→S，a.s.

最后由Kronecker引理得：

从而定理得证.