基于极点配置和Pade近似的空调温度控制器的设计

何天磊， 朱其新

（1.苏州科技大学 环境科学与工程学院，江苏 苏州 215009；2.苏州科技大学 机械工程学院，江苏 苏州 215009）

在空调温度控制过程中，在一定的条件下，其被控对象可以看成一个具有时滞的一阶环节[1-3]，该时滞的存在增加了系统的控制难度，降低了系统的控制品质。传统PID 控制作为最常用的一种控制方式，由于其参数易整定等特点而被广泛应用。但对于具有时滞的对象，PID 控制常常得不到令人满意的控制效果。

Smith 预估补偿控制是最早应用于时滞系统控制的方法，其通过引入一个补偿器，以削弱时滞对系统性能的影响。但由于Smith 预估补偿控制太过于依赖精确的数学模型，在预测模型存在一定的误差时，控制效果将大大下降[4-6]。后来提出的达林算法特点是将期望的闭环响应设计成一阶惯性加纯延迟，然后反过来得到满足这种闭环响应的控制器，其优点是结构简单，控制系统的鲁棒性好，但其实际应用效果较差[7-8]。自适应控制通过修正控制参数以适应对象和扰动的动态特性的变化，所以自适应控制对系统参数有良好的适应能力，但其依赖被控对象的数学模型，也较难以实际应用[9-11]。

笔者提出的基于极点配置和Pade近似的空调温度控制器的新设计，一方面利用极点的分布和系统性能的密切关系，使闭环系统的极点配置在期望的位置，从而使空调温度控制系统具有优良的动态性能[12-15]；另一方面利用Pade近似算法将空调温度控制系统的传递函数的模型简化。Pade近似往往比泰勒级数准确，所以其具有适应范围广，更容易实现的优势[16-18]。仿真结果证明，文中提出的基于极点配置和Pade近似的PID控制比传统的PID 控制和Smith 预估补偿控制具有更好的控制效果。

1 空调系统温度控制的对象模型

在满足一定控制精度的情况下，空调系统的实际温度控制对象可以采用一个一阶的模型来描述被控对象的动态特性，考虑到温度对象的滞后性，空调系统温度控制模型可表示为[19]

其中，G1（s）表示被控对象的传递函数，T 为被控对象的时间常数，K 为放大系数，τ 为温度对象的延迟时间。

2 基于极点配置和Pade近似的控制器设计

2.1 Pade近似算法

e-τs是一个无理函数，在系统中直接分析会比较困难，所以通常用有理函数近似来代替延时环节e-τs，以简化设计过程。文中采用Pade近似算法，其表达式为

其中，l，k 的值越大，近似就越精确。当l＝k 时，一阶的表达式为

由（1）式和（3）式可得被控对象的传递函数

控制系统结构图如图1 所示。

图1 控制系统结构框图

其中，G1（s）表示被控对象的传递函数，G2（s）表示设计的控制器。用Gp（s）表示控制系统的传递函数，显然有

2.2 极点配置的控制器设计

由（4）式可知被控对象的传递函数为一个二阶模型，拟采用的控制器为PID 控制器，用G2（s）表示

根据公式（4）和公式（6）可得

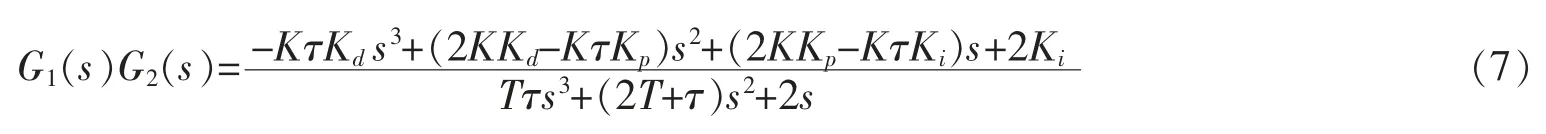
根据公式（5）和公式（7）易得

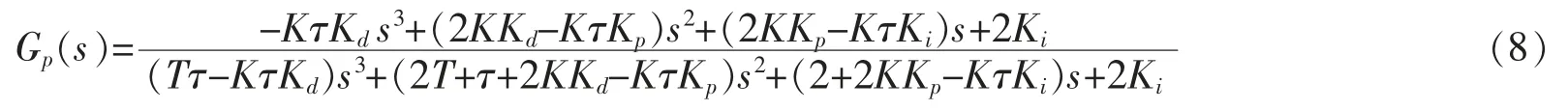
闭环系统的特征方程为

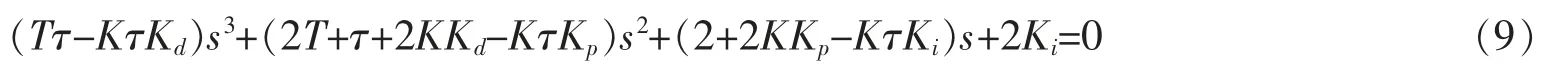
由于系统的性能主要由系统的特征根确定，对于三阶系统而言，比较理想的情况是其两个特征根中有一对共轭极点和在负半轴上有一个实极点，即希望系统的特征方程为

其中，ωn为系统的无阻尼振荡频率，ξ 为阻尼比，ω0为第三个实数极点离坐标原点的距离。

整理得

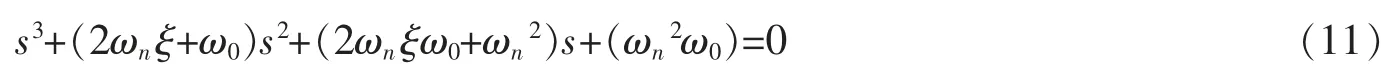
即希望

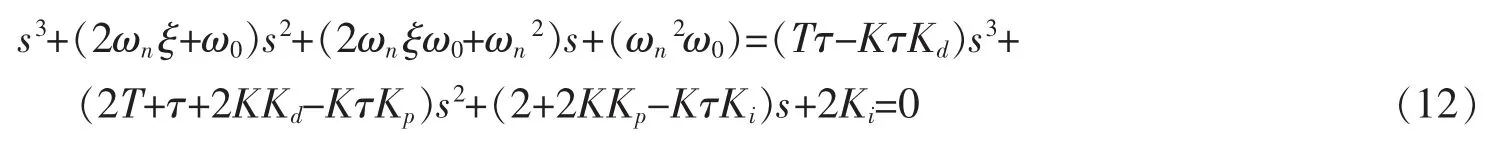
由公式（12）可以得

由公式（12）和公式（13），得

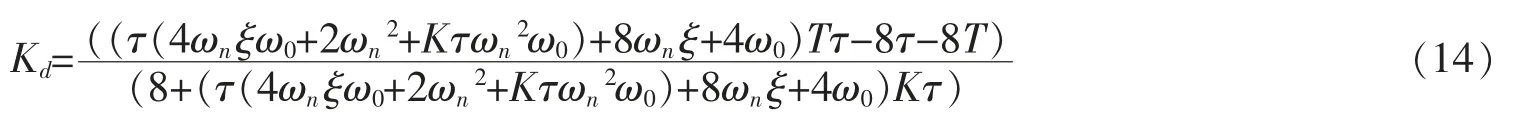
由公式（12）、（13）和（14），得

在ωn、ξ、T、K 等参数都已知的情况下，由公式（14）、（15）和（16）可以得到参数Kp、Ki和Kd的值。ωn的大小决定了系统的响应速度，ωn越大，系统响应越快，但ωn太大会导致系统不稳定。为了使系统具有较大的稳定裕度，同时又具有较快的响应进度，ξ 一般在0.6 到0.8 之间取值，通常取0.707。

3 控制系统仿真

为了验证文中提出的控制器的控制效果，用MATLAB 进行模拟仿真。根据公式（1），一般空调系统温度控制中常取时间常数为T＝200，延迟时间取τ＝10，增益系数K＝1，所以空调系统温度控制的模型为

空调系统温度控制的Simulink 仿真模型如图2 所示。

图2 系统结构图

其中输入信号为阶跃信号。

图3 是传统PID 控制的响应曲线图，传统PID控制器的三个控制参数是按BTN 公式整定得到[20]，且Kp＝21.6，Ki＝1.03，Kd＝103。从图3 中可以看出传统PID 控制不仅超调较大，而且响应时间较长。图4 是Smith 预估补偿控制的响应曲线图，Smith 预估补偿控制的系统中PID 控制器的控制参数即传统PID 控制中利用BTN 公式整定出的参数值。由图4分析，虽然系统震荡比用传统PID 控制器控制小很多，但是仍然有较大的超调。图5 是基于极点配置和Pade近似算法的PID 控制仿真波形图， 其PID控制参数是利用极点配置方法计算得到，三个控制参数值为：Kp＝9.23，Ki＝0.05，Kd＝11.0。由图5 可知，应用极点配置和Pade近似的新型PID 控制器的系统响应无超调且运行平稳，而且系统在60 s 就可以达到稳定状态，响应时间比传统PID 控制和Smith 预估补偿控制短很多。所以基于极点配置和Pade近似的PID 控制比传统PID 控制和Smith 预估补偿控制具有更好的动态特性。

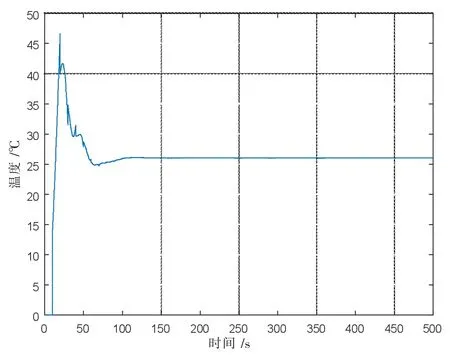
图3 PID 控制系统的闭环响应曲线

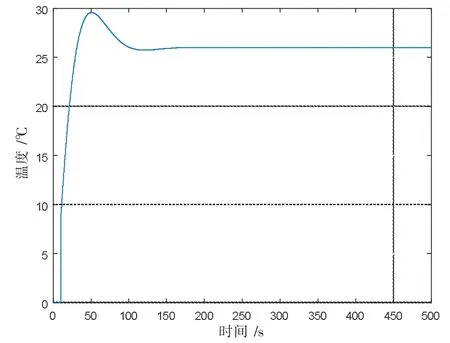
图4 Smith 预估补偿控制系统的闭环响应曲线

图5 应用文中控制器的系统的闭环响应曲线

为了验证文中提出的基于极点配置和Pade近似的PID 控制器的鲁棒性，文中对空调系统温度预估模型和实际温度控制模型存在误差时的三种控制方法的控制效果进行仿真，即在预估模型不做任何改变情况下，将实际模型的增益系数由1 调整为0.5，实际模型的其他参数不变。预估模型存在误差的空调温度控制系统结构图，如图6 所示。

图6 预估模型存在误差时系统的结构图

三种控制方法中PID 控制器的三个参数都与预测模型存在误差前一样。图7、8、9 是传统PID 控制器、Smith 预估补偿控制器和基于极点配置和Pade近似法控制器在预测模型和实际存在偏差情况下， 仿真出的系统响应曲线图。由图7、8 看出，当预估模型出现误差时，传统PID 控制和Smith 预估补偿控制系统响应稳定时间和预估模型没有误差时响应时间明显加长很多，震荡也在一定程度上加大，说明传统PID 控制器和Smith 预估补偿控制器对模型的依赖性较大。由图9 看出，基于极点配置和Pade近似法的控制运行响应时间也加长了较多， 但是响应过程很平稳， 表明该控制器具有较强的鲁棒性。所以文中提出的基于极点配置和Pade近似法的控制比传统PID 控制和Smith 预估补偿控制具有更好的控制性能。

图7 模型存在误差时传统PID 控制器的闭环响应曲线

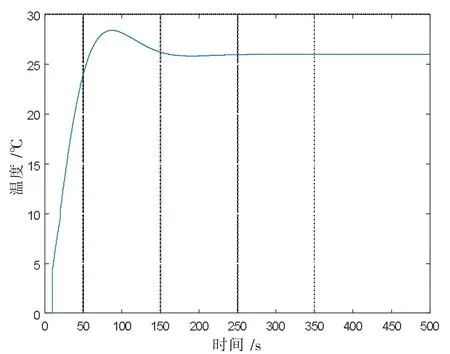
图8 模型存在误差时Smith 预估补偿控制器的闭环响应曲线

4 结语

笔者提出了一种基于极点配置和Pade近似的空调温度控制器设计的新方法，该方法结合了极点配置和Pade近似算法两者的优点， 有效解决了时滞对空调系统温度控制的影响。仿真结果证明，相比于传统PID 控制和Smith 预估补偿控制， 文中提出的基于极点配置和Pade近似的控制器具有更好的动态性能和更强的鲁棒性。文中的方法也适用于具有时滞的其他被控对象，具有一定的应用和推广价值。

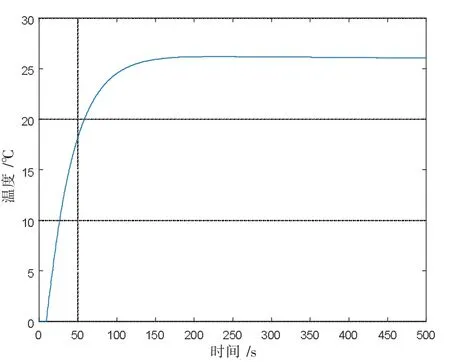
图9 模型存在误差时文中提出的控制器的闭环响应曲线