努尔森扩散对崔家沟煤温度压力吸附所作贡献的数值分析

张学梅，马青华，郝静远，李 东

(西安思源学院 能源及化工大数据应用教学研究中心，西安 710038)

0 前 言

在推导无机膜气体分离的温度-压力-气体渗透率方程时[1]，综合考虑努尔森(Knudsen)扩散和表面扩散后得到理论方程，方程中包含4个有物理意义的参数A、B、和β。温度的影响由参数表示，而压力的影响由参数β表示。参数A和参数B与扩散介质有关，其中参数A是唯一与努尔森扩散有关的参数，也被称为多孔介质的几何形体常数。基于气体渗透与气体吸附的相似性，衍变出仍有4个参数(A、B、和β)和相同数学形式的温度-压力-气体吸附方程(Temperature Pressure Adsorption Equation)，参见式(1)。

(1)

式中,V为吸附量，cm3/g；M为分子量，甲烷的分子量为16；T为绝对温度，K；P为压力，MPa;A为对于1个固定的多孔介质的微孔几何形体常数,与努尔森扩散有关的参数；B为吸附流量系数，与吸附区域相关;：在吸附质流中的1个吸附分子的最低势能和活化能之间的能量差(K)，主要衡量吸附温度的相对影响；β为类似于Freundlich 吸附等温线方程中的压力参数，主要衡量吸附压力的相对影响。

方程(1)可称为“完整TPAE”，显示吸附由努尔森扩散吸附与表面扩散吸附构成。努尔森扩散吸附量与热力学温度的平方根成反比，而表面扩散吸附量则是温度与压力的函数。由于吸附(包括努尔森扩散吸附与表面扩散吸附)是温度和压力的函数，则在数学上讨论温度变化和压力变化对吸附量的共同影响，采取将方程(1)进行全微分，而计算方程(1)的全微分相当复杂、繁琐。若方程(1)中参数A=0，完整的TPAE简化成以下方程：

(2)

方程(2)可称为“简化TPAE”， 显示当忽略努尔森扩散吸附量后，吸附仅由表面扩散吸附构成。对简化TPAE进行全微分，比对完整TPAE进行全微分较为容易。尽管已将简化TPAE的全微分用于多种场合[2-9]，且知道参数A=0的物理意义是忽略努尔森扩散吸附量，但从未计算过努尔森扩散吸附量的大小，也未比较过忽略努尔森扩散吸附量所产生的影响。以下以陕西焦坪崔家沟7号煤的系列等温吸附数据为例[10]，就努尔森扩散对温度、压力吸附所作贡献进行数值分析。

1 数据处理

由于在说明温度-压力-气体吸附方程回归样本的建立与计算中[11]已列出陕西焦坪崔家沟7号煤的特征参数、系列实测条件、兰氏体积和兰氏方程参数，同时描述回归样本集的建立以及完整TPAE的4个参数确定，在此不复述。适用于陕西焦坪崔家沟7号煤的4个参数见表1。

表1 陕西焦坪崔家沟7号煤的4个参数

将表1的4个参数代入方程(1)，得完整TPAE在不同温度和压力条件下的完整吸附量(VZ)。将表1的3个参数(因为A=0)代入方程(2)，得简化TPAE在相应的温度和压力条件下的简化吸附量(VJ)。Vz大于VJ的部分即可计算努尔森扩散吸附量。即每一组V完整(VZ)与V简化(VJ)之间的相对差别(δ)即可知晓努尔森扩散吸附量的大小。

(3)

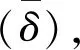
(4)

将以上计算结果列于表2，其相对平均差别仅为0.03%。

表2 陕西焦坪崔家沟7号煤在不同温度和压力条件下完整吸附量(Vz)与简化吸附量(VJ)

温度/k压力/MPaVzVJδ0.54.71 4.71 0.05 16.66 6.66 0.04 29.41 9.40 0.03 311.51 11.51 0.02 293413.29 13.29 0.02 514.85 14.85 0.02 616.27 16.26 0.02 717.57 17.56 0.01 818.78 18.77 0.01 0.53.91 3.91 0.06 15.53 5.53 0.04 27.81 7.81 0.03 39.56 9.56 0.03 303411.03 11.03 0.02 512.33 12.33 0.02 613.50 13.50 0.02 714.58 14.58 0.02 815.59 15.58 0.02 0.53.29 3.29 0.07 14.65 4.65 0.05 26.57 6.56 0.04 38.04 8.04 0.03 31349.28 9.27 0.03 510.37 10.37 0.02 611.35 11.35 0.02 712.26 12.26 0.02 813.11 13.10 0.02 0.52.80 2.80 0.08 13.96 3.95 0.06 25.59 5.58 0.04 36.84 6.84 0.03 32347.89 7.89 0.03 58.82 8.82 0.03 69.66 9.66 0.02 710.43 10.43 0.02 811.15 11.15 0.02

2 讨 论

(1)当气体在多孔固体中扩散时，如果孔径小于气体分子的平均自由程，则气体分子对孔壁的碰撞较之气体分子间的碰撞频繁得多，该种扩散称为努尔森(Knudsen)扩散。从表2数据可看出，在所测的温度、压力范围内，努尔森扩散吸附对总的吸附贡献很小，其相对平均误差仅为0.03%。

(2)当气体的密度逐渐加大(吸附压力增加)时，虽多孔固体的孔径不变，但气体分子的平均自由程却逐渐减少，类似液体中的平均自由程很小，故努尔森扩散吸附逐渐不显著。比如在50 ℃进行吸附时，0.5 MPa吸附压力下努尔森扩散吸附对总的吸附贡献为0.08%；而6 MPa吸附压力下，努尔森扩散吸附对总的吸附贡献仅为0.02%。

(3)当气体分子的平均自由程逐渐增加(吸附温度增加)，虽多孔固体的孔径不变，努尔森扩散吸附对总的吸附贡献逐渐增加。如同样在0.5 MPa吸附压力下，在20 ℃进行吸附时，努尔森扩散吸附对总的吸附贡献为0.05%；在50 ℃进行吸附时，努尔森扩散吸附对总的吸附贡献却增加为0.08%。

(4) 在恒温条件下，简化TPAE也变成含有二常数项的指数方程，类似于Freundlich 等温吸附方程。在恒温条件下，简化TPAE尽管也是含有二常数项的指数方程，但其系数项是温度的函数，而指数项却不是温度的函数。Freundlich 吸附等温线方程也是含有二常数项的指数方程，其系数项、指数项均为温度的函数。

3 结 论

吸附由努尔森扩散吸附与表面扩散吸附构成，而努尔森扩散的大小是由气体分子的平均自由程与多孔固体的孔径之比的大小所决定。任何可以增加气体分子的平均自由程的方法(增加温度、减少压力)均可增加努尔森扩散吸附对总吸附量的贡献。但在所测的温度(20 ℃～50 ℃)、压力(0.5 MPa～8 MPa)范围内，努尔森扩散吸附对总的吸附贡献很小，其相对平均误差仅为0.03%。在恒温条件下，简化TPAE尽管也是含有二常数项的指数方程，但其系数项是温度的函数，而指数项却不是温度的函数。