遗传算法优化BP神经网络预测股指研究

谢梦蝶 秦江涛

摘 要：股票价格受众多不确定性因素影响。为更精准地预测股票指数，首先利用具有良好非线性寻优能力的遗传算法优化BP网络初始权值阈值设置，然后构建一个以开盘价、最高价、最低价、收盘价、成交量、收盘价近5日移动平均线MA等6个输入变量、以下一天6个变量为输出变量的股指预测模型。对观察期内上证综指实证研究表明，经遗传算法优化后的BP 网络对股票指数预测平均误差为0.1%，其中成交量预测值比单纯BP神经网络算法误差减少0.71%，同时收敛速度得到提高。

关键词：BP神经网络;遗传算法;股指预测

DOI：10. 11907/rjdk. 191185

中图分类号：TP306文献标识码：A文章编号：1672-7800（2019）004-0041-05

0 引言

股市波动会对金融市场产生重大影响，甚至影响到经济发展。如果能较好地预测股票指数走势，则可及时调控引导股市，对投资者给予指导。

股价预测存在的问题主要有：①股价数据中含有较多噪声[1]，股指指数编制不合理，大型机构造市行为及外部影响等因素引起股市的强烈波动;②股价本身以及影响股价的各变量之间呈非线性特性[2];③股票市场的主体是具有主观能动性的投资者，不确定的投资行为使股价难以预测;④我国股市明显的政策特征[3-4]。

但股票价格并非完全随机，而是与历史数据、宏观经济因素、技术面等相关。人工神经网络ANN（Artificial Neural Network）作为最准确的软计算技术广泛应用在许多领域的预测模型中，这些领域包括社会、工程、经济、商业、金融、外汇、股票等[5-6]。Pesaran等[7]根据过去25年伦敦证券指数数据，采用神经网络技术预测指数的月变化情况，正确率达到60%;王上飞等[8]从非线性时间序列预测角度，使用滑动窗技术与径向基函数神经网络对IBM公司股票进行预测，曲线拟合效果较好。

股票市场是一个极其复杂的非线性动力学系统，而神经网络具有分布处理、自组织、自适应、自学习和容错性等优良特性，在处理股价预测这种多因素、不确定和非线性的时间序列预测问题方面具有独特优势。

Yudong等[9]提出了一种改进的细菌趋化性优化，集成到反向传播人工神经网络预测各种股票指数，实验表明该预测模型比其它方法在学习能力和泛化能力方面性能更好;Kara等[10]对支持向量机和神经网络算法进行比较，实验证明神经网络算法更优;Adebiyi等[11]利用纽约证券交易所的股票数据探讨自回归积分移动平均模型ARIMA（Autoregressive Integrated Moving Average Model）和人工神经网络模型的预测性能，实证结果显示神经网络模型比ARIMA模型优越;Qiu等 [12]利用神经网络对日经平均指数进行预测，搜集了71个输入指标，利用模糊曲线最终选出18个具代表性的输入指标，成功预测了股票市场收益;胡照跃等[13]首先利用主成分分析法采用贡献率达90%的主成分，再用附加动量法优化BP神经网络预测股价，取得更小的误差和更少的运行时间;黎镭等[14]利用GRU递归神经网络预测上证中的18支股票未来10天的收盘价，精度达到98%。于卓熙[15]首先利用主成分分析法对股票价格指标降维，再利用广义回归神经网络预测股票价格，比ARIMA模型结果更精准。

上述文献表明，神经网络及其衍生模型能够在股票市场预测方面取得较好的结果。BP神经网络（Back Propagation）算法对于初始权值阈值的设置非常重要，如果设置不当，不仅会导致网络训练速度慢，而且容易陷入局部最优[16]。针对这一问题，本文利用具有良好非线性寻优能力的遗传算法优化BP 网络初始权阈值设置，以此提高预测模型性能。

1 BP神经网络与遗传算法

1.1 BP神经网络原理

BP网络采用反向传播算法，利用梯度下降原理对网络参数进行调节，以最好的拟合进行训练样本集合[17]，使神经网络的输出值和目标值之间的误差平方最小化，梯度下降收敛到训练误差相对于网络权值的局部极小值。

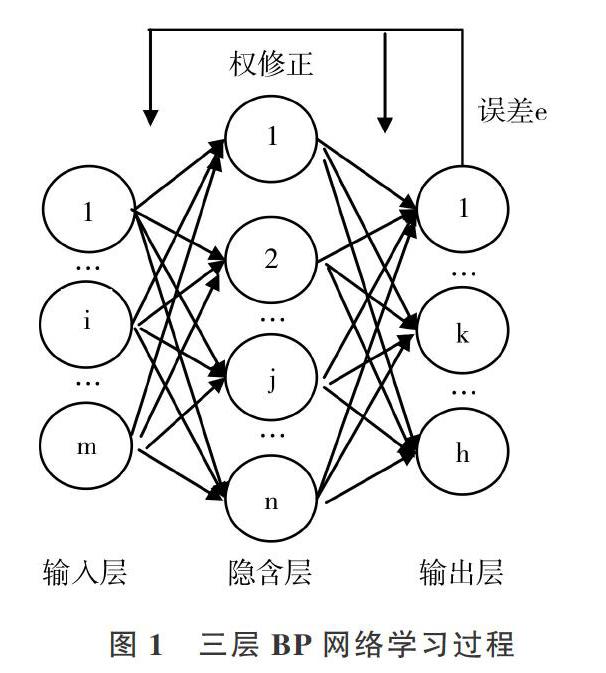
一个具有m个输入、一个隐含层和h个输出的三层神经网络模型结构如图1所示。

1.2 遗传算法优化BP神经网络原理

遗传算法[18]GA（Genetic Algorithm）是一种仿生群智能算法，它从任一初始种群出发，通过随机选择、交叉和变异等操作，产生一群更适应环境的个体，使种群逐步进化到搜索空间中越来越好的区域。遗传算法是一种不依赖于辅助信息的启发式全局搜索算法，在搜索过程中不易陷入局部最优，这一点正好可以弥补BP 网络的不足[19]，所以本文采用遗传算法优化BP神经网络权值阈值的初始设置。

2 股指预测模型设计

2.1 神经网络设计

2.1.1 输入层和输出层设计

神经网络结构设计涉及到选择网络的隐层数、隐含层节点数和输入层输出层节点数。由于三层前馈网络能以任意精度逼近任何连续的非线性函数[20]，因此本文选用只有一个隐层的三层BP网络。

为了预测时刻t+n的数据，需收集并分析从时刻t+n-m到时刻t+n-1的历史数据，然后找出预测值与历史数据之间的联系。由于预测量为第二天的开盘价OPEN、最高价HIGH、最低价LOW、收盘价CLOSE、成交量V、收盘价近5日简单移动平移MA等6个变量，因而输出层神经元数目为6。

2.1.2 确定隐层节点数

隐层节点数量的选择是一个复杂问题[21]，通常采用试凑法确定最佳的隐层节点数，即先设置较少的隐层节点作为初始值，然后逐渐增加隐层节點数，最后选择误差最小时所对应的隐层节点数。采用试凑法时可将一种粗略估计隐层节点数的公式作为初始值参考。

2.1.3 激活函数与训练函数选择

初始化参数时，选取激活函数为S型函数。S型函数因为具有可微且非线性特点，所以能够强化网络的非线性映射能力。神经网络传递函数通常采用连续可微的Sigmoid函数。本实验隐含层的传递函数确定为tan-sigmoid函数，输出层的传递函数确定为线性激活函数。

本文用迭代次数和收敛精度作为评价指标，经多次训练模型发现，Levenberg-Marquardt算法的迭代次数最少，收敛精度表现最佳，故本文网络模型采用trainlm作为训练函数。

2.2 遗传算法优化神经网络

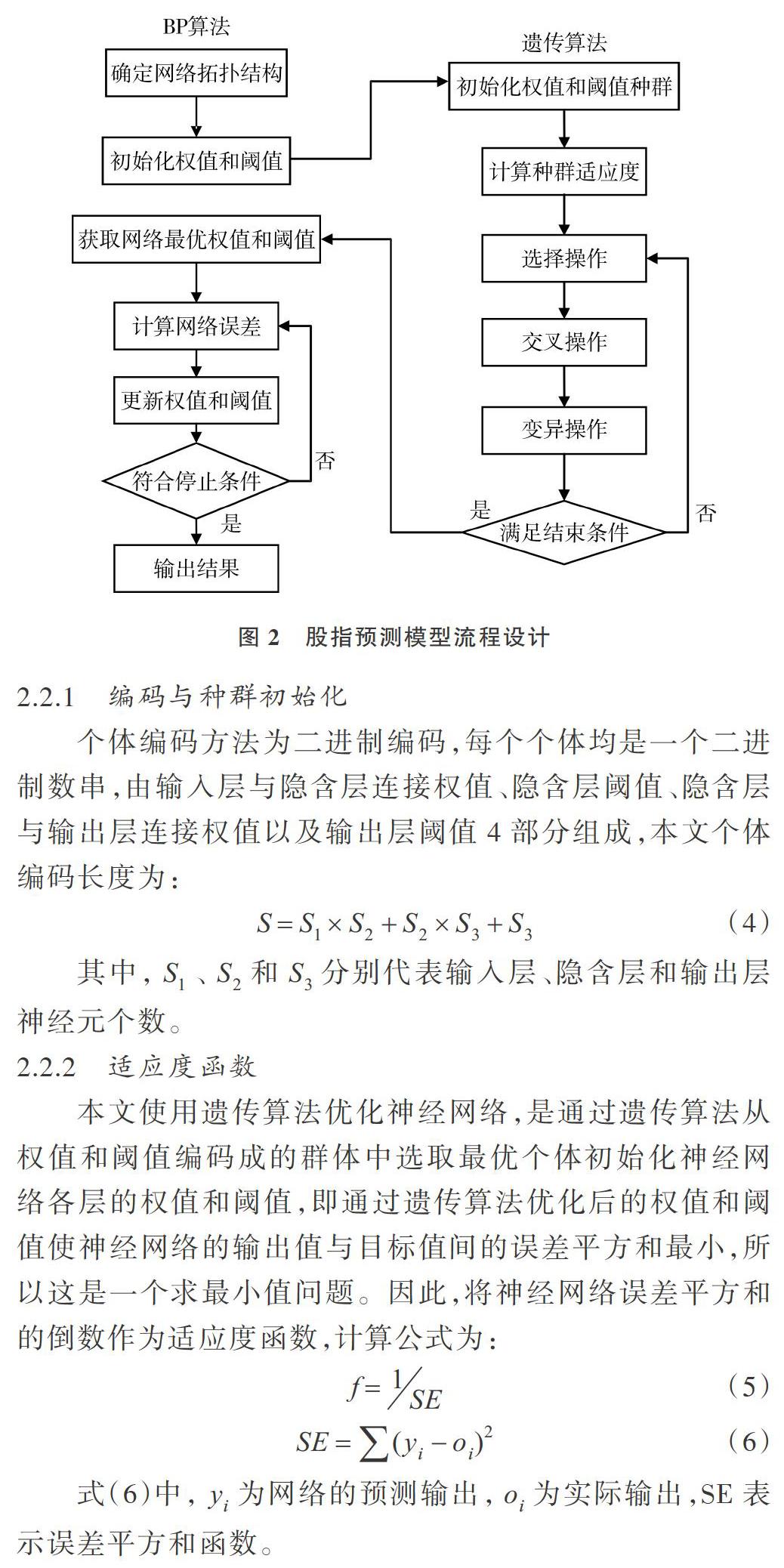
遗传算法一般从3个方面优化神经网络：①利用遗传算法训练神经网络的权值和阈值;②利用遗传算法确定神经网络的拓扑结构;③二者结合进行。本文模型利用遗传算法的目的是优化BP神经网络的权值和阈值。种群中的個体通过适应度函数计算得出个体适应度值，然后通过选择、交叉和变异操作，找出最优个体。利用最优个体对网络权值和阈值进行赋值，网络训练后经输出层输出，最后经过反归一化得到预测值。具体流程如图2所示。

2.2.1 编码与种群初始化

个体编码方法为二进制编码，每个个体均是一个二进制数串，由输入层与隐含层连接权值、隐含层阈值、隐含层与输出层连接权值以及输出层阈值4 部分组成，本文个体编码长度为：

2.2.2 适应度函数

本文使用遗传算法优化神经网络，是通过遗传算法从权值和阈值编码成的群体中选取最优个体初始化神经网络各层的权值和阈值，即通过遗传算法优化后的权值和阈值使神经网络的输出值与目标值间的误差平方和最小，所以这是一个求最小值问题。因此，将神经网络误差平方和的倒数作为适应度函数，计算公式为：

2.2.3 遗传算子控制参数

（1）群体规模。本文利用训练样本通过多次训练，选择种群规模为50。

（2）选择操作。本文采用轮盘赌选择方法确定个体的生存和淘汰。轮盘赌选择是从群体中选择一些个体，被选中的机率和个体的适应性分数成比例，个体的适应性分数愈高被选中的概率也愈高。

（3）交叉操作。本文采取简单算术交叉，交叉概率为0.95。

（4）变异操作。本文采用的变异操作是非一致变异，变异概率为0.1。

（5）算法终止条件。通过多次训练模型，最后选择最大进化代数为100。

3 实验与结果分析

3.1 数据选取

选取2016年1月14日至2016年11月10日共200个交易日的上证指数作为原始数据（数据来源于通达信金融终端），选择上证指数开盘价OPEN、最高价HIGH、最低价LOW、收盘价CLOSE、成交量V、收盘价近5日简单移动平移MA等6个输入变量，将200组数据前2/3作为训练样本，后1/3作为测试样本，依次将顺序5天的数据作为一个样本输入数据，将其后一天的收盘价作为BP神经网络的输出目标。原始数据如表1所示。

3.2 股指预测

本文利用MATLAB神经网络工具箱GOAT构建网络模型，预测模型包括输入层、隐含层和输出层的三层BP神经网络。构建BP神经网络需要不断调整网络的隐层节点数和其它参数，根据模型的预测误差确定最佳的网络结构。设定最大迭代次数为2 000次，学习速率为0.3，最小均方误差目标为0.000 1。

对于普通的BP网络，取学习期为5天，学习期的每天选取股市交易数据输入指标：上证指数的开盘价OPEN、最高价HIGH、最低价LOW、收盘价CLOSE、成交量V、收盘价近5日简单移动平移MA等6个。因此，网络输入层节点个数为5×6=30。

隐层结点个数经验公式如下：

由上述经验公式可知，隐含层节点数的大致范围为5-16个。为了加快训练的收敛速度，适当扩大范围，分别对隐含层5-28的节点数进行网络建模分析，找出合适的隐层结点数。网络结构的其它设置不变，对原始数据采用BP网络进行实验分析。

从表2可以看出，当隐含层节点数为24时，BP神经网络模型的迭代次数和收敛精度都达到最小，同时网络的训练时间也在合理区间内。因此，选定神经网络模型的拓扑结构为30-24-6。BP网络结构、预测效果如图3、图4所示。

3.3 预测实验结果对比

用遗传算法优化BP神经网络进行实验。从图5可以看出，经过50步迭代，适应度达到稳定。适应度值小是因为计算误差平方和SE时成交量这一变量值过大，但这不影响后续结果误差率的对比。下面以预测10天收盘价为例对比观察，如表3所示。

上证指数在BP神经网络和基于遗传算法优化的神经网络中，开盘价、最高价、最低价和收盘价预测误差统计如表4所示。

由表3可知，GA-BP网络对上证指数预测的准确率相对BP网络都有提升，但提升的幅度不统一，其中收盘价平均误差只有0.1%，成交量平均误差下降了0.71%，这和遗传算法的稳定性较差有直接关系，但达到了利用遗传算法优化网络的实验目的。单纯采用BP神经网络预测股指时会出现初始权值设定随意性大、收敛速度慢、平均误差大等缺点，但经遗传算法优化后的BP神经网络改善了以上问题。

上证指数在两种不同算法下的收敛速度如图6、图7所示。

由图6、图7可知，利用BP神经网络迭代210次才达到目标收敛精度，而基于遗传算法优化的BP神经网络在经过147次迭代后便收敛。可见，基于遗传算法优化的BP神经网络在收敛速度要优于BP神经网络。

4 结语

BP神经网络由于初始权值阈值的设置容易导致网络训练速度慢、陷入局部最优等问题。本文采取具有非线性寻优特点的遗传算法优化BP神经网络权值阈值，构建上证指数的开盘价OPEN、最高价HIGH、最低价LOW、收盘价CLOSE、成交量V、收盘价近5日简单移动平移MA等为输入变量，下一天的6个变量为输出变量的GA-BP 神经网络股指预测模型，分别从6个变量的平均误差率角度对比分析了BP 网络优化前后的预测结果。对比单纯的BP神经网络，6个指标预测误差率得到不同程度提升，平均误差率为0.1%，收敛速度得到加快。实验结果表明，基于遗传算法优化的BP神经网络在预测股指方面优于单纯的BP神经网络，可为投资者提供更准确的股票市场趋势预测数据。

参考文献：

[1] 欧阳洪. 中国股市噪声交易行为有效性实证研究[J]. 山东财政学院学报，2007（4）：20-22.

[2] 周洪涛，王宗军. 上海股市非线性特征：一个基于R/S方法的实证分析[J]. 管理学报，2005，2（5）：597-600.

[3] 胡金焱. 中国股票市场宏观政策效应的实证研究[J]. 经济学动态，2003（6）：22-24.

[4] 肖小锋. 中国政策市的行为思考[J]. 华东经济管理， 2003， 17（5）：94-95.

[5] KHASHEI M，BIJARI M. An artificial neural network （p， d， q） model for timeseries forecasting[J]. Expert Systems with Applications， 2010， 37（1）：479-489.

[6] ZHANG G，PATUWO B E， HU M Y. Forecasting with artificial neural networks： the state of the art[J]. International Journal of Forecasting， 1998，14（1）：35-62.

[7] PESARAN M H，TIMMERMANN A. A recursive modelling approach to predicting UK stock returns[J]. Economic Journal，2010，110（460）：159-191.

[8] 王上飞，周佩玲，吴耿峰，等. 径向基神经网络在股市预测中的应用[J]. 预测，1998（6）：44-46.

[9] YUDONG Z，LENAN W. Stock market prediction of S&P 500 via combination of improved bco approach and bp neural network[J]. Expert Systems with Applications， 2009， 36（5）：8849-8854.

[10] KARA Y，BOYACIOGLU M A，BAYKAN O K. Predicting direction of stock price index movement using artificial neural networks and support vector machines： the sample of the istanbul stock exchange[J]. Expert Systems with Applications， 2011， 38（5）：5311-5319.

[11] ADEBIYI A A，ADEWUMI  A  O，AYO  C  K. Comparison of ARIMA and artificial neural networks models for stock price prediction[J]. Journal of Applied Mathematics，2014（1）：1-7.

[12] QIU M，SONG Y，AKAGI F. Application of artificial neural network for the prediction of stock market returns： the case of the Japanese stock market[J]. Chaos Solitons & Fractals the Interdisciplinary Journal of Nonlinear Science & Nonequilibrium & Complex Phenomena， 2016， 85（9）：1-7.

[13] 胡照跃，白艳萍. 基于改进BP神经网络的股票预测[J]. 经贸实践，2016（2）：153-157.

[14] 黎镭，陈蔼祥，李伟书. GRU递归神经网络对股票收盘价的预测研究[J]. 计算机与现代化， 2018（11）：98-102.

[15] 于卓熙，秦璐，趙志文. 基于主成分分析与广义回归神经网络的股票价格预测[J]. 统计与决策， 2018（18）：62-67.

[16] 李永明. 人工神经网络BP学习算法的研究及在人脸识别中的应用[D]. 济南：山东大学， 2012.

[17] 陈蓓蓓.基于主成分分析与神经网络的股票价格预测[D].天津：南开大学， 2011.

[18] 王小平，曹立明. 遗传算法：理论、应用及软件实现[M]. 西安：西安交通大学出版社， 2002.

[19] 兰胜坤. 遗传算法优化BP神经网络的说话人识别系统[J]. 重庆理工大学学报， 2013， 27（10）：91-95.

[20] 何成刚，张燕平，张站. 机器学习中知识动态获取在函数逼近中的探究[J]. 微计算机信息， 2010， 26（27）：134-136.

[21] 刘要来，周红波，荀小伟. 基于BP神经网络的渗流场反演分析[J]. 中国水运，2014，14（10）：113-116.

（责任编辑：杜能钢）