面向LoRa网络的基于维纳滤波的RSSI定位算法

莫建麟

(阿坝师范学院，四川 阿坝州 623002)

0 引 言

定位是物联网(Internet of Things, IoT) 的多数应用应用的基础。尽管全球定位系统(Global Positioning System, GPS)是解决多数定位问题的常用策略[1]，但是利用GPS获取IoT内设备位置并不是最有效的方式。一方面，GPS成本高、功耗大；另一方面，GPS系统的室内定位性能差。

远距离无线电(Long Range Radio, LoRa)是由Semtech公司创建的低功耗局域网无线标准。它以功耗低、传输距离远而著称。目前，LoRa广泛应用于室外无线传输，覆盖范围可达到30 km～50 km。采用啁啾扩频调制(Spread Spectrum Modulation, CSS)，LoRa实现了长距离、低功耗通信[2]。

长距离、低功耗的特性，使LoRa广泛在室外和室内IoT场景中广泛使用。此外，基于LoRa通信不仅可以用于数据传输，也可无需增加额外设备环境下计算节点位置。以GHz为工作频段，LoRa信号具有高的墙体穿透性，且对多径衰落也具有鲁棒性[3]。

目前的一些研究成果已证实，LoRa技术能够应用于定位系统[4]，但是仍缺失有效的实验数据。研究人员对LoRa通信中基于到达时间(Time of Arrival, ToA)、到达时间差(Time Difference of Arrival, TDoA)、到达角度(Angle of Arrival, AoA)定位进行了一些研究工作。

然而，基于AoA定位算法要求天线阵列，而基于ToA/TDoA定位算法依赖于准确时钟，并且基于TDoA定位算法要求节点间同步。相比之下，基于接收信号强度指标(Received Signal Strength Indicator, RSSI)的定位算法实施简单，无需额外设备。

目前，针对LoRa通信中基于RSSI定位的研究工作较少。文献[5]针对室外噪声环境中的LoRa场景，分析了基于RSSI定位算法。而文献[6]针对LoRa室内应用，提出基于RSSI测距估计。此外，文献[7]的研究表明，在室内环境，LoRa能够提供可接收的定位误差。但是在室外环境，定位误差达到几百米。

因此，需设计合适的算法，提高基于LoRa系统内基于RSSI定位算法的精度。滤波技术，如粒子群、贝叶斯和Kalman滤波，常用于定位系统。通过滤除噪声环境内的噪声数据，提高定位精度。

为此，针对LoRa通信的室内和室外环境，提出基于维纳滤波的RSSI定位算法(Wiener Filter-based RSSI Localization, WFRL)。WFRL算法利用维纳滤波降低测距误差，提高定位精度。

1 LoRa物理层概述

LoRa技术通过改变物理层参数实现调制分集。这些参数包括：频度宽度B、扩频因子S和编码率Rc。其中，扩频因子S=log2Nc，Nc表示每个符号内的码片数[8]。

而调频率等于频度宽度B，因此一个符号的时长T等于2S/B。此外，LoRa物理层包含了一个转发错误校正码，它的编码率Rc等于4/(4+n)，其中n∈1,2,3,4。由于一个符号包含S个信息比特位，信息速率Rb：

(1)

不同扩频因子S和编码率Rc，可形成10种物理层模式，如表1所示。WFRL算法就是充分利用模式的多样性，即在不同模式下，获取RSSI的测量值[9]。将这些RSSI值作为维纳滤波的输入，通过维纳滤波滤除噪声数据。表1中Sensitivity表示对信号的灵敏度。

2 WFRL算法

2.1 基于RSSI测距模型

先依据Friis传输等式建立RSSI值与距离d间关系，如式(2)所示，其中d是指接收端与发送端间距离。

P=-(10αlgd-A)

(2)

其中A表示当接收端与发送端距离为1m时，接收端所接收的功率，单位为dBm。而P为接收端所接收的功率。α为路径衰落指数。

图1 信号传输模型

依据式(2)，估计距离d：

(3)

从式(3)可知，参数A和α对测距精度有影响。并且，不同的环境，它们的值并不相同。为此，WFRL算法利用LoRa不同模式下的RSSI值，训练这两个参数，进而获取LoRa信道特性[10]。最后，依据LoRa信道特性，并结合RSSI的均值测距，再利用定位算法估计节点位置。

2.2 基于维纳滤波的测距

(4)

依表1可知，LoRa有10种不同的模式。为此，可利用LoRa不同模式下RSSI的均值估计距离。即利用所测量的RSSI值的权重平均估计距离[11]，进而提高测距精度。令Nm表示使用的LoRa模式数，且Nm≤10。

(5)

对式(5)进行数学变换：

(6)

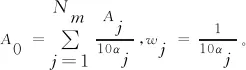
引用权重矢量w=[ω1,ω2,…,ωNm]，其反映了在LoRa不同模式下的权重系数。接下来，分析如何计算权重矢量w。

先建立距离对数的均方误差等式：

(7)

将式(6)代入式(7)，再建立偏微分方程，如式(8)所示：

(8)

再利用霍夫方程(wiener-Hopf equation)求解式(8)，可得：

(9)

其中RP={rP(k)}为自相关矩阵。其中rP(k)=E{Pj(i)P(i)}，且k=j-。

而rd={rd(k)}为互相关矢量，其定义如式(10)所示：

rd(k)=E{[A0-lgd(i)]Pk(i)}

(10)

其中j,=1,2,…Nm。

2.3 质心定位算法

利用三角质心定位算法估计节点位置。图2显示了三角质心定位原理。先获取到三个锚节点的距离，三个锚节点(A、B、C)再以距离值建立三个圆。圆的交点(Xa,Xb,Xc)形成三角形，三角形的质心位置就是节点的位置。

图2 三角质心定位算法

2.4 定位模型

考虑如图3所示的定位系统，系统内有多个锚节点，这些节点已知自己位置。实际上，这些锚节点就是LoRa发射器，它们发射信号。而未知节点通过接收信号，估计与锚节点间距离。理论上，在二维平面内，未知节点只需获取与三个锚节点距离，就能估计自己的位置。

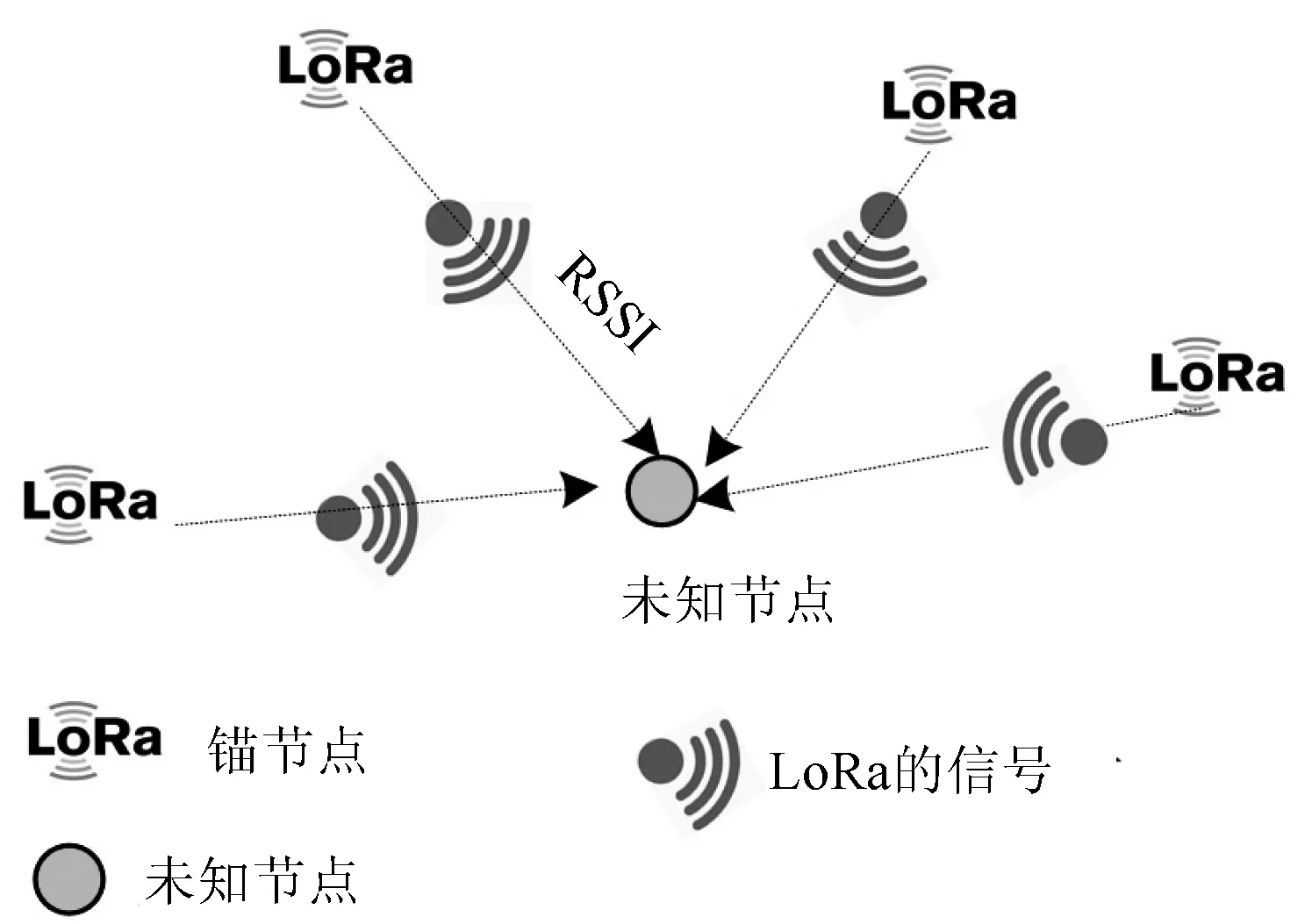
图3 定位模型

锚节点先以不同模式传输信号，未知节点利用(6)估计距离，获取了距离信息后，再利用三角质心算法估计位置。

3 性能仿真

3.1 信道特性分析

3.1.1场景建立

本节分析室内和室外两个场景下的信道特性，如图4所示。对于室内信道，考虑长为37 m的走廊，且走廊边上有几个房间。并考虑LOS和NLOS这两个信道环境。(1)LOS信道：将发射器和接收器均放在走廊里；(2)NLOS信道：将发射器放在走廊边上的房间里，接收器放在走廊。最初，发射器离接收器为5m，再以5m为一步长，将它们距离的拉长至35m。同时测量每种LoRa模式下的100个RSSI值，用于训练室内的LoRa信道特性。

图4 室内和室外环境

在街道上测量LoRA信道特性。考虑330 m的街道，并将节点架在2 m上方。与室内环境一样，固定接收器，移动发射器。两个设备距离从20 m～330 m，步长为20 m。并采集不同距离下100个RSSI值，用于训练室外的LoRa信道特性。室外环境只考虑LOS情况。

3.1.2LoRa信道数据分析

表2显示了两个室内和室外环境下的RSSI值。选择了LoRa模式1、模式5和模式10三个通信模式下的参数A和α值。

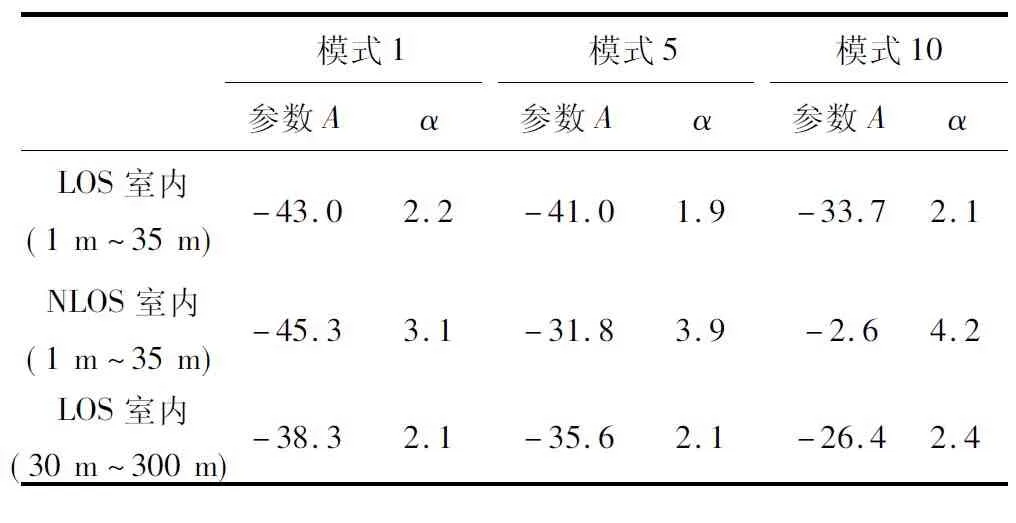
表2 不同LoRa模下的A和α值

从表2可知，LoRa模式对参数A和α值较大影响，且存在小幅度范围内的波动。此外，同在室内环境下，NLOS信道下的衰落指数α大于LOS信道的衰落指数。这符合事实。

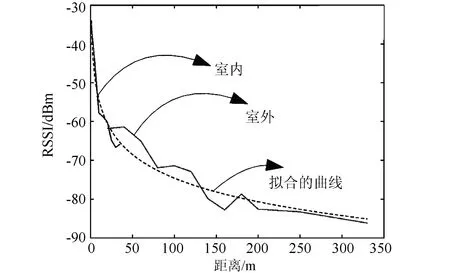
图5 RSSI值随距离变化曲线

将所收集的RSSI值进行拟合，形成RSSI值(dBm)与距离间的关系曲线，如图5所示。从图可知，室内长距离的RSSI值逼近于室外短距离的RSSI值。这就将室外和室内的信道特性拟合成一条曲线。此外，由于指数特性，距离越长, RSSI曲线越平。

3.2 性能对比分析

为了更好地分析维纳滤波处理RSSI性能，选择文献[12]的RSSI算法(标记为RSSI-A)作为参照。对比分析WFRL算法和RSSI-A的测距误差性能和定位误差性能。

表3显示了RSSI-A和WFRL算法对室内环境的测距误差。其中RSSI-A-1表示只利用LoRa模式1采集的RSSIs值方法；WFRL-1表只利用LoRa模式1采集的RSSIs值的维纳滤波方法；而RSSI-A-average、WFRL-average表示10个模式下的平均值。

表3 测距误差(单位m)

表3显示了基于平均RSSI和最大RSSI数据下的测距性能。相比于RSSI-A算法，WFRL算法的测距误差得到有效控制。例如，在只利用LoRa模式1环境下，WFRL算法的测距误差为5.3 m，而RSSI-A算法的测距误差达到14 m。此外，相比于10种模式下的平均值，仅通过模式1获取RSSI值更有利于测距精度的提高。

图6显示了RSSI-A算法和WFRL算法的平均定位误差。从图可知，相比于RSSI-A算法，提出的WFRL算法在平均定位误差得到有效控制，这归功于测距精度的提高。这些数据表明，利用维纳滤波能够有效地滤除RSSI噪声数据。

图6 平均定位误差

4 结 语

针对LoRa系统的定位问题，提出了基于维纳滤波的RSSI定位算法WFRL。WFRL算法通过维纳滤波处理来自LoRa不同模式的RSSI值，进而提高了测距和定位精度。并通过实验测量了LoRa通信的室内和室外的信道特性，用数据证实：在LoRa系统内，基于RSSI测距能够获取可接收的定位精度。而利用维纳滤波可进一步提高定位精度。