基于双弯曲质点弹簧系统的Waterbomb铺嵌快速模拟
2019-06-07于丽洁孙红岩
于丽洁 孙红岩
摘 要:通过对Waterbomb铺嵌模型的结构分析,提出双弯曲质点弹簧系统并对其进行模拟。根据与棱相邻的三角形面片是否对称,将Waterbomb铺嵌模型的非边界棱(边)归为两类,建立两类弯曲弹簧,设置不同的弯曲弹性系数,该质点弹簧系统被称为双弯曲质点弹簧系统。然后运用隐式欧拉法和块坐标下降法求解最小化问题,得到下一时刻物体运动变形的速度和位置,实现对Waterbomb铺嵌模型快速、稳定和准确的模拟。实验证明,在误差允许范围内,该算法速度快于牛顿法。相比单弯曲(基本)系统,双弯曲质点弹簧系统提升了模拟稳定性、真实性,并减小了误差。
关键词:质点弹簧系统;弹性变形模拟;薄壳;Waterbomb折纸铺嵌;双弯曲质点弹簧系统
DOI:10. 11907/rjdk. 181788
中图分类号:TP317.4文献标识码:A文章编号:1672-7800(2019)001-0186-06
Abstract:According to the analysis of waterbomb tessellation model structure, bi-bending mass-spring system is proposed to simulate waterbomb tessellation. According to the symmetry of the triangular facets adjacent to the edge, the non boundary edges of the waterbomb tessellation model are classified into two classes, and two kinds of bending springs are established with different bending elasticity coefficients. This mass-spring system is called the bi-bending mass-spring system. Then, we use the implicit Euler method and solve the minimization problem by block coordinate descent method (also known as alternating optimization) to get the velocity and position of the movement and deformation of the object at the next time. This paper realizes the fast, stable and accurate simulation of waterbomb tessellation model. Within the allowable error range, the algorithm is faster than Newtons method. Compared with the single bending (basic) system, the bi-bending mass-spring system further improves the stability and realism of the simulation and reduces the error.
0 引言
基于物理的模拟方法符合客观物体运动和变形规律,能够很好地保持运动和变形的真实性。在基于物理的模拟中,模型的表示方法包括质点弹簧模型、有限元模型、无网格表达等。质点弹簧模型由一系列质点和连接各个质点的弹簧构成,是一种最简单的弹性体模拟方法,在图形学中得到了快速发展。不同种类的弹簧具有不同特性。
在图形学的物理模拟中,薄壳容易弯曲、宽度与厚度之比大于100,在未变形状态下是弯曲的结构[1]。而与之相对的薄板在未受力状态下是平整的。常见的薄壳结构有轿车外壳、草帽、纸张、鸡蛋壳、树叶等。
纸张本身是刚性的薄壳结构。当纸张被折叠,形成具有负泊松比的铺嵌模型时,纸张整体便具有了弹性,成为柔性曲面,可形成各种形状。折纸(Origami)既是一种古老的艺术形式,又是一种很好的娱乐方式。人们可以通过折纸艺术将具有水密性的硬质材料如纸张、金属等通过弯曲或折叠形成复杂的三维形状。
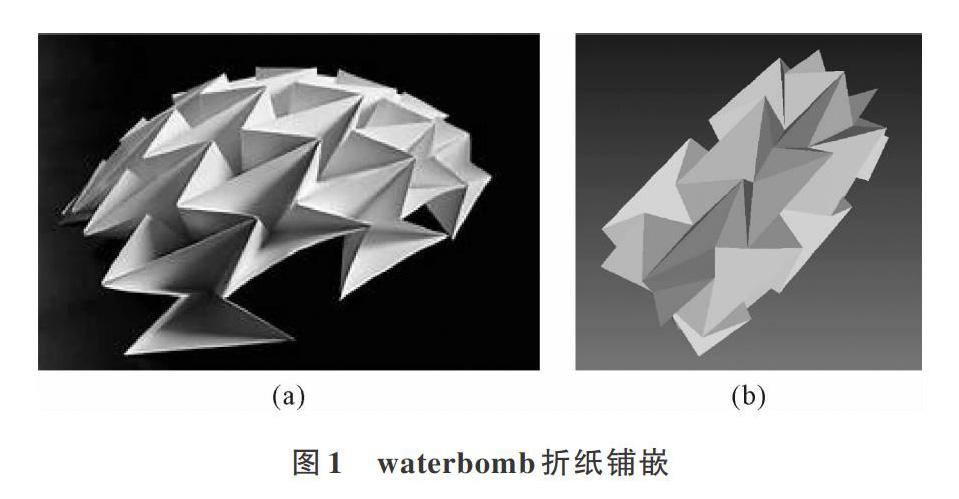
拼嵌模式包括waterbomb tessellation、Miura-ori、Yoshimura pattern、Resch's pattern、Curved folding、Huffman's Origami Tessellations等。Waterbomb样模铺嵌或水雷铺嵌是应用最广泛的折纸图案之一。它是基于三角形可平面折叠的图案模式,具有周期对称,泊松比为负,属于具有各向异性的拉涨材料[2]。Waterbomb样模铺嵌的负泊松比特性通过刚性的完整纸张折叠得到,无需通过剪切实现。Waterbomb样模分为六折痕样模和八折痕样模[3],两种样模可形成不同的铺嵌模型。由于曲面既有凹点也有凸点,因此Waterbomb铺嵌具有足够的柔性,可形成多种折纸图案[4]。
1 相关工作
质点弹簧模型原理简单,易于操作,在更加注重模拟速度和稳定性、而不十分注重模拟精度的实时模拟中应用广泛。2009年,Lu等[5]用双层质点弹簧系统对植物叶片进行模拟。2013年,刘雪梅等[6]基于粘弹性力学模型耦合无网格伽辽金与质点弹簧对软组织进行形变仿真,在大变形和拓扑改变区域使用无网格伽辽金法,其它区域使用质点弹簧法,两个区域之间建立过渡单元。高精度及与拓扑无关的无网格伽辽金法与高效简单的质点弹簧组合的方式有效解决了精度与效率平衡的问题,实现了高精度实时形变仿真。2013年,陈瑛等[7]根据织物拉伸形变过程中受力与形变程度的非线性关系特征,提出分段线性化弹性系数的改进质点弹簧模型,解决了织物模拟中超弹性的问题,提高了模拟真实感。2013年,Liu等[8]将隐式欧拉方法转换为能量最小化问题,并引入弹簧方向作为辅助未知变量,用块下降法对最小化问题进行求解,实现了对质点弹簧系统的快速实时模拟。2015年,王崴等[9]对绳索形变进行模拟,将传统正方形质点弹簧网格进行改进,提出一种蜂窝状的弹簧质点模型,利用Verlet-梯形预测-校正法进行数值積分以求得下一时刻速度和位置。实验结果表明,蜂窝状质点弹簧模型有效,算法提高了计算效率和精确度。2017年,王舒珍等[10]在传统四边形模型的基础上对质点弹簧模型进行改进,去除剪切弹簧,以结构弹簧代替,对软组织形变进行模拟。
自1987年Terzopoulos等[11]对弹性变形物体进行模拟后,基于物体的模拟方法被成功运用到立体、薄壳、布料、流体的变形模拟中。在薄壳模拟中,2003年,Grinspun等[1]提出了一种简单的离散薄壳模型,该模型无需重复之前模型复杂的连续介质力学公式和算法。该方法主要关注不可拉伸的薄壳,即薄壳的变形主要为等距变换。弯曲能量用相邻面片二面角的变化进行描述。在此基础上,2007年Garg等[12]提出实现更简单、计算更高效的基于折叶(hinge-based)的物理模型,对易弯曲或接近刚性的、各向同性或各向异性的薄板或薄壳进行模拟。一个弯曲折页由两个相邻三角形面片形成。由于折页的方法简单,计算复杂度低,在网格模型模拟中大受欢迎。2014年,Bouaziz等[13]提出投影动力学,能够支持一系列几何约束,在同一框架中对立体、布料、薄壳进行基于实例的模拟。其中,薄壳的弯曲能量用变形状态下和未变形状态下平均曲率的变化(差的平方)描述。对于等距变换,该弯曲能量可以用附加的(auxiliary)旋转矩阵重写为拉普拉斯-贝尔特粒米算子,然后用分段线性的帽子基函数(hat basis)将该连续弯曲能量进行离散化。2016年,Zhang等[14]提出用交互工具对3D中空打印模型变形进行设计。根据模型各部分弯曲弹性的不同,中空模型各部分被设计成不同厚度。2017年,Liu等[15]将投影动力学解释为拟-牛顿法,并用L-BFGS进行加速,能够支持多种不同超弹材料的模拟,包括新虎克弹性材料和基于样条的材料。
在折纸领域方面,2003年Grinspun等[1]提出可通过修改标准布料模拟器快速实现离散薄壳模型。2006年,Burgoon等[16]以该薄壳模型为基础,考虑了纸张弹性,提出将纸张折叠成为简单模型的交互界面。该方法没有重点处理折痕多的纸张间碰撞问题,折出了简单的折纸模型,如5个折痕的小狗模型。2010年,Tomohiro Tachi在文獻[4]中提出设计三维自由曲面的方法和Freeform Origami 系统,可对给定的图案进行自由编辑;在文献[17]中,Tomohiro Tachi提出一种折出任意三维形状的方法Origamizer Method, 可将材料折叠成给定多面体的折痕图。2013年,Tomohiro Tachi[18]研究了由给定多面体曲面设计Resch式折纸铺嵌自由形状的方法;在文献[19]中,Tomohiro Tachi提出交互式模拟和设计折纸的计算方法,其中折纸形状由每个样模(图元,基本型)弯曲情况决定。2013年,Davis等[20]对David Huffman的折纸铺嵌进行了重建。
2 Waterbomb铺嵌上的双弯曲质点弹簧系统
2.1 模拟对象
本文对图1(a)所示的折纸铺嵌图案类型进行模拟,其模拟模型来自Tomohiro Tachi的Freefrom Origami系统[4],见图1(b)。
2.2 双弯曲质点弹簧系统
Waterbomb铺嵌模型的质点弹簧模型主要包括结构弹簧和弯曲弹簧。
将纸张沿折线向上折叠,称为峰折或山折(moutain fold),向下折叠称为谷折(valley fold),向上向下折两次称为中性折(genderless fold),带有折痕模式的纸张平面图称为折痕图或CP图(crease pattern),最基本的折痕图称为waterbomb 样模(base)、图元或基本型,将一组waterbomb 样模在三维空间按照一定规律重复拼嵌便组成waterbomb 铺嵌或拼嵌(tessellation)。Waterbomb样模边界边、峰折折痕和谷折折痕统称为边(或棱)。
六折痕Waterbomb样模解析如图2所示。
2.2.1 结构弹簧
在所有棱(包括Waterbomb样模边界边、峰折折痕和谷折折痕)上设置结构弹簧,如图3中直线所示。
2.2.2 弯曲弹簧
(1)单弯曲弹簧。将所有弯曲弹簧均使用同一弹性系数的质点弹簧系统称为单弯曲质点弹簧系统。以单个Waterbomb样模为例,对如何建立其铺嵌模型质点弹簧系统中的弯曲弹簧进行说明。单个Waterbomb样模的质点弹簧模型如图3所示。
对于薄壳结构来说,弯曲变换是一个重要变换。根据对图2的分析,本文以棱为中心(面向棱)构建Waterbomb弯曲弹簧,如图3中的虚线点状曲线所示。例如,与边OB相邻的三角形分别为三角形OBE和三角形OBD,其上与边OB相邻的顶点分别为点E和点D。连接ED,建立在边OB上的弯曲弹簧。
(2)双弯曲弹簧。由于Waterbomb铺嵌模型变形时具有各向异性特性,本文在系统中设定具有不同弯曲弹性系数的弯曲弹簧,即双弯曲质点弹簧系统。仍然以单个Waterbomb样模为例说明Waterbomb折纸铺嵌模型双弯曲质点弹簧系统的构建(见图4)。通过对Waterbomb样模铺嵌的结构进行分析,发现根据棱两边三角形面片结构是否对称,可以将Waterbomb铺嵌模型非边界棱分为3类:①与棱相邻的两个三角形面片关于棱是轴对称的,该类棱包括:峰折折痕(如边OE)和Waterbomb样模中边界较长的边(如边BD);②与棱相邻的两个三角形面片关于棱是中心对称的,该类棱包括Waterbomb样模中边界较短的边(如边EB);③与棱相邻的两个三角形面片关于棱不具有对称性,该类棱包括谷折折痕(如边OB)。
以棱为中心,根据不同类型的棱(面向棱)构建Waterbomb的弯曲弹簧(见图4)。
根据以上分析,本文将Waterbomb折纸样模铺嵌模型的棱(或边)分为3类。本文将与棱两边相邻的三角形面片对称(包括轴对称和中心对称)的第1、第2类棱统称为Ⅰ类棱,Ⅰ类棱包括Waterbomb样模所有边界边和“峰折”折痕;将与棱两边相邻的三角形面片不具有对称性的第3类棱统称为Ⅱ类棱。
本文在Ⅰ类棱和Ⅱ类棱上分别建立弯曲弹性系数不同的弯曲弹簧。将Ⅰ类棱上的弯曲弹簧称为峰弯曲弹簧(或者相同弯曲弹簧),Ⅱ类棱上的弯曲弹簧称为谷弯曲弹簧(或者不同弯曲弹簧)。
图4展示了一个Waterbomb样模的双弯曲质点弹簧构建。以棱OE为例:与棱OE相邻的三角形面片为三角形OEB和三角形OEA,从而与棱相对顶点为点A和点B。因此对于棱OE,本文连接邻接点点A和点B建立相同弯曲弹簧AB。同理,在棱OB上连接邻接点点E和点D,建立谷弯曲弹簧ED或不同弯曲弹簧ED。
3 基本概念与受力分析
设所模拟物体质点数为[m],经历的离散时刻依次为[t1,t2,t3,?],时间步长用[h]表示。物体在时刻[tn]的位置坐标为[qn∈R3m]。系统所受的力用非线性函数表示为[f:R3m][→R3m],则[tn]时刻系统所受的力为[f(qn)]。[f=-?E],其中[E]为包括内部力和外部力的势能函数,[E:R3m→R]。
设[M∈R3m×3m]为对角质量矩阵,[vn]为[tn]时刻的速度。
物体所受的力包括内力和外力。内力是指质点间的相互作用力,主要有弹性变形产生的力。本文中内力主要是弹簧弹性力。根据胡克定律,弹簧弹性势能为:[Es=12kp1-p2-r2]。其中,[k]是弹性系数,[r]为弹簧原长([r0]),[p1,p2∈R3]为弹簧的两个端点。外力指物体受到的外部作用力,包括物体本身的重力、外界施加的力、碰撞反应力、风力等。本文暂时只考虑物体所受的重力。外力[fext=Mg],其中[g]为重力常数。
4 数值方法
本文采用文献[8]的隐式欧拉法和数值求解方法。
4.1 隐式欧拉法
4.2 数值求解
最小化问题可用块坐标下降法(又称交替优化法)求解,以下称为local-global方法。首先,为[x]指定一个初始猜测值[y]。在局部过程中,固定[x]计算最优的[d];在全局过程中,固定[d]计算最优的[x]。一直重复该过程直到收敛或达到最大迭代次数。
5 实验结果与分析
本部分首先从误差、稳定性及模拟速度方面,对单弯曲(基本)质点弹簧模型的实验结果进行分析和讨论,确定迭代次数和弯曲弹性系数的范围,然后对双弯曲质点弹簧系统的实验结果进行分析讨论。
本文实验环境为64位Windows10 操作系统,Intel(R) Core(TM) i56300HQ CPU@ 2.30GHz 。本文采用的实验模型如图1所示,该模型质点个数为67,边数为170,三角形面片数为104。在实验中,设定时间步长为[h=1/30s],质点总质量为10g,结构弹簧拉伸弹性系数为80,重力常量为10kg/N,阻尼系数为0.001。
5.1 参数范围
单弯曲质点弹簧模型即基本质点弹簧模型。本文首先用单弯曲质点弹簧模型确定模拟参数大致范围。
5.1.1 实验效果
从图5可以看出,與没有弯曲弹簧相比,有弯曲弹簧的质点弹簧系统模拟的Waterbomb铺嵌模型折痕不会随时间慢慢展平,很好地保持了模型变形的细节特征,由此说明弯曲弹簧的重要性。双弯曲质点弹簧系统对弯曲弹簧进行细分,提高了模拟精确性。
5.1.2 误差与稳定性分析
其中,[x0]为初始的预测值([x0=y]),[x*]为采用牛顿法迭代到收敛时的值,[xi]表示第[i]次迭代时的位置。从定义可以看出,将由牛顿法得到的值作为基准(“准确值”)。相对误差主要描述了算法的收敛性,“绝对误差”则表示由本文算法得到的位置与准确值之间的差异。
在物理模拟中,模拟速度和精度往往是一对矛盾。本文综合模拟速度和精确度对Waterbomb结构的弯曲弹性系数进行选择,并设置结构弹簧拉伸系数均为80。
在单弯曲质点弹簧系统中,本文采用不同的弯曲弹性系数检测算法收敛性。弯曲弹性系数分别为10、20、100、500时的相对误差值,如图6所示。其中,相对误差值是综合第30、60、90帧后得到的平均值。
从图6可以看出,本文将Tiantian Liu等[8]提出的质点弹簧快速模拟方法运用在Waterbomb样模铺嵌模型的模拟时,对于不同的弯曲弹性系数,该方法最终均可收敛。整体而言,弯曲弹性系数越低,收敛速度越快。
此外,实验结果证实,相对误差并不是迭代次数的递减函数。当迭代次数为20次或30次时,相对误差增大,有些帧的相对误差远远大于1。相对误差描述了快速模拟方法相对于牛顿法的收敛情况。对实验结果整理后发现,[g(x0)-g(x*)<0]即[g(x0) 本文分别在图6和图7中描绘了弯曲弹性系数为10、20、100、500时相对误差和绝对误差的曲线,经综合分析可知,相对误差和绝对误差最终均会收敛。 除去弯曲弹性系数[bs=20]的情况,可以发现弹性弯曲系数越大,相对误差和绝对误差越小,收敛速度越快。当[bs=10]时,相对误差和绝对误差尤其小:相对误差最大在1左右。 综上分析,当弯曲弹性系数[bs=10]时,实验中的相对误差和绝对误差均最小。由此,本文选择弹性弯曲系数为10对Waterbomb样模铺嵌进行模拟。 5.1.3 模拟速度分析 在物理模拟中,除了精确度外,模拟速度是一个重要因素,而模拟精确度和速度往往不能兼顾。实验记录了迭代次数分别为10、15、20、30、40时各数值方法的计算效率数值,如表1所示。 在表1中,当迭代次数分别为10、15、20、30、40时,本文算法(local-global)的fps数值依次递减,分别为19.5、14、11、7.5、5.6,即随着迭代次数增多,模拟速度降低。牛顿迭代法的fps数值均为11,这是因为本文所用的Waterbomb模型的复杂度较低,当迭代次数分别为10、15、20、30、40时,牛顿法已经收敛。 5.1.4 参数范围确定 在单弯曲质点弹簧系统中,从模拟效果、误差及稳定性、模拟速度方面综合考虑,通过对实验结果进行讨论分析,选择迭代次数为15、弯曲弹性系数小于等于10。此时,模拟稳定,误差在允许范围内,并且模拟速度快于牛顿法。 5.2 双弯曲质点弹簧模型 5.2.1 实验效果 根据实验结果,选择相同弯曲弹性系数[sb=5],不同弯曲弹性系数[db=10],迭代次数为15,对Waterbomb样模铺嵌模型进行模拟。实验结果如图8所示。 5.2.2 误差与稳定性分析 双弯曲质点弹簧系统的Waterbomb折纸模型模拟的相对误差和绝对误差曲线如图9、图10所示。 从图9可以看出,双弯曲质点弹簧系统中的相对误差比单弯曲质点弹簧系统更稳定、误差更小(保持在1附近及以下)。从绝对误差方面来看,当[sb=5,db=10]时,双弯曲质点弹簧系统的绝对误差数量级为10-4,在误差允许范围内,如图10所示。相对误差和绝对误差的计算综合了第30、60、90帧误差的平均值。图10帧数较少,大致描绘了误差走势。 在物理模拟中,模拟速度和精度往往是一对矛盾。根据对Waterbomb的结构分析,综合模拟速度、精确度及稳定性,本文选择弯曲弹性系数为5、不同弯曲弹性系数为10、迭代次数为15时对Waterbomb折纸模型进行物理模拟。此时,模拟稳定性良好,误差在允许范围内,并且速度快于牛顿法。 5.2.3 参数确定 首先,在单弯曲质点弹簧模型上,对模拟Waterbomb铺嵌模型的参数进行初步确定;然后,根据Waterbomb铺嵌模型结构特征,建立双弯曲质点弹簧系统。实验结果证明,相对于单弯曲质点弹簧系统,双弯曲质点弹簧系统的稳定性更好、误差进一步降低;最终选择模拟参数为:相同弯曲弹性系数等于5、不同弯曲弹性系数等于10、迭代次数等于15。此时,算法模拟速度快于牛顿法。 6 结语 本文根据基本质点弹簧模型确定参数范围,为Waterbomb铺嵌的每条边均建立结构弹簧,并以每条非边界边为基础建立弯曲弹簧。采用隐式欧拉法和块坐标下降法(或交替优化法)求解方程,得到物体运动变形的下一位置坐标。通过对实验效果的误差及稳定性分析发现,当迭代次数为15、弯曲弹性系数小于等于10时,模拟效果稳定、误差在允许范围内且效果真实。然后,根据与棱相邻的三角形面片是否对称,将非边界棱归为两大类,并设定不同的弯曲弹性系数,建立双弯曲质点弹簧系统。实验结果表明,相对于单弯曲质点弹簧系统,双弯曲质点弹簧系统进一步提升了稳定性、减小了误差、提高了模拟真实性。本文实现了对Waterbomb铺嵌模型的稳定模拟,在误差允许范围内,模拟速度比牛顿法更快。双弯曲质点弹簧系统进一步提高了模拟稳定性、降低了模拟误差。 本文没有建立对角相望弹簧。在Waterbomb样模中,如图4中的E点和F点之间会发生弯曲,但是在本文算法中并没有建立该弯曲弹簧。因为该弯曲弹簧是基于点的,而本文弯曲弹簧是基于棱建立的。因此,在以后的研究中,可尝试基于点建立质点弹簧系统。另外,本文将与棱相邻的三角形面片是轴对称还是中心对称视为同种情况(对称)处理的做法不够精确。由于弹簧对二面角的符号不敏感,所以本文并不是严格意义上的薄壳,但是由于Waterbomb铺嵌的结构特性,运用质点弹簧对其进行模拟的做法也得到了很好的效果。 参考文献: [1] GRINSPUN E,HIRANI A,DESBRUN M,et al. Discrete shells [C]. Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation, 2003: 62-67. [2] RAFSANJANI A, PASINI D. Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs[J]. Extreme Mechanics Letters,2016, 9: 291-296. [3] CHEN Y,FENG H,MA J,et al. Symmetric waterbomb origami [J]. Proceedings of the Royal Society of London,2016,472 (2190):1-20. [4] TACHI T. Freeform variations of origami[J]. Journal for Geometry and Graphics,2010, 14(2): 203-215. [5] LU S, ZHAO C,GUO X,et al. Bi-layered mass-spring model for leaf motions[J]. Journal of System Simulation,2009,21(14):4343-4388. [6] 劉雪梅,毛磊,李运华,等. 耦合无网格伽辽金与质点弹簧实现软组织形变仿真[J]. 计算机辅助设计与图形学学报,2013,25(1):1-6. [7] 陈瑛,吴明珠,胡新荣. 一种改进的质点-弹簧织物建模与仿真[J]. 华南师范大学学报:自然科学版,2013, 45(5):43-46. [8] LIU T,BARGTEIL A W,O'BRIEN JAMES F,et al. Fast simulation of mass-spring systems[J]. ACM Transactions on Graphics,2013,32(6):803-812. [9] 王崴,周诚,杨云,等. 基于改进弹簧-质点模型的柔性绳索仿真[J]. 计算机辅助设计与图形学学报,2015,27(11):2230-2236. [10] 王舒珍,陈国栋,李琦. 基于改进的质点-弹簧模型的软组织形变仿真研究[J]. 通化师范学院学报,2017(1):64-69. [11] TERZOPOULOS D,PLATT J,BARR A,et al. Elastically deformable models[C]. Conference on Computer Graphics & Interactive Tec,1987:205-214. [12] GARG A,GRINSPUN E,WARDETZKY M,et al. Cubic shells[C]. Siggraph/Eurographics Symposium on Computer Animation, 2007: 91-98. [13] BOUAZIZ S,MARTIN S,LIU T,et al. Projective dynamics: fusing constraint projections for fast simulation[J]. ACM Transactions on Graphics,2014,33(4):1-11. [14] ZHANG X,LE X,WU Z,et al. Data-driven bending elasticity design by shell thickness[J]. Computer Graphics Forum,2016,35(5):157-166. [15] LIU T,BOUAZIZ S,KAVAN L,et al. Quasi-Newton methods for real-time simulation of hyperelastic meterials[J]. ACM Transactions on Graphics,2017,36(3):1-16. [16] BURGOON R,WOOD Z J,GRINSPUN E. Discrete shells origami[C]. Proceedings of the 21st International Conference on Computers and Their Applications, 2006:180-187. [17] TACHI T. Origanizing polyhedral surfaces[J]. IEEE Transactions on Visualization and Computer Graphics,2010, 16(2): 298-311. [18] TACHI T. Designing freeform origami tessellations by generalizing Resch's patterns[C]. Proceedings of ASME 2013 IDETC/CIE, 2013:1-10. [19] TACHI T,OBREBSKI J B, TARCZEWSKI R. Interactive form-finding of elastic origami[C]. Proceedings of the International Association for Shell and Spatial Structures(IASS) Symposium,2013:23-27. [20] DAVIS E, DEMAINE E D, DEMAINE M. L, et al. Reconstructing David Huffman's origami tessellations [C]. Proceedings of the ASME 2013 International Design Engineering Technical Conferences & Computersand Information in Engineering Conference, 2013:1-10. (責任编辑:江 艳)
