基于MEEMD与TEO的电缆故障测距方法

田书 周令 孙永超

摘 要：正确识别故障行波波头和精确的双端测距算法可保障电缆故障行波测距精度。为解决希尔伯特黄变换（HHT）中经验模态分解（EMD）存在的模态混叠问题，提出一种基于改进集总经验模态分解（MEEMD）和Teager能量算子相结合的电缆故障行波检测方法。针对故障行波波速及线路实际长度变化对双端测距精度的影响，推导出一种不受波速影响的双端测距算法。PSCAD/EMTDC仿真结果验证了该方法可行且测距精度高。

关键词：电缆故障;集总经验模态分解;Teager能量算子;双端行波测距

DOI：10. 11907/rjdk. 181055

中图分类号：TP319文献标识码：A文章编号：1672-7800（2019）001-0144-04

Abstract：Correct identification of fault line wave head and accurate double-terminal traveling wave distance measuring ensure the accuracy of cable fault travel wave distance measurement. In order to solve the problem of modal aliasing in the empirical mode decomposition （EMD） in Hilbert Huang transform（HHT），a new method based on modified ensemble empirical mode decomposition （MEEMD） and Teager energy operator is proposed for the traveling wave fault location. The problem of the influence of the fault traveling wave velocity and the actual length of the line on double-terminal traveling wave distance measuring accuracy，double-terminal traveling wave distance measure is proposed which is not affected by wave velocity. The effectiveness and high precision of the proposed method are demonstrated by PSCAD/EMTDC simulation results.

0 引言

随着现代城市的发展，城区内电力电缆被广泛应用于配电网中。由于土地资源愈加稀缺，同时为了美化城市环境，电缆一般呈蛇形敷设在地下，传统巡线方式进行故障排查已无满足电缆测距要求[1]。因此，研究精确、高效的电力电缆故障定位方法具有重要的工程实用价值。行波法被公认为理论上最准确的故障测距方法。行波测距的关键问题之一是行波波头的准确标定 [2]。目前行波波头的标定方法主要有小波分析和希尔伯特黄变换（HHT）方法。小波分析通常运用于非奇异信号检测且需要根据不同情况选择合适的基函数和分解尺度[3-4]。HHT方法是一种能够处理奇异信号的自适应分解算法。通过经验模态分解（EMD）将故障信号分解得到首个固有模态函数（IMF1）分量，对其进行希尔伯特变换，通过分析时频特性曲线标定波头到达时刻。由于EMD分解会出现模态混叠现象，即不同时间尺度的信号出现在同一个IMF分量中[5-8]，因此利用该方法进行故障测距时误差较大。集总经验模态分解（EEMD）在EMD方法的基础上添加高斯白噪声，虽然一定程度上消除了模态混叠现象，但是会出现噪声残余的问题[9]。改进的集总平均经验模态分解方法（MEEMD）不仅有效抑制了模态混叠现象，还消除了白噪声残余，能够真实地还原原始信号[10]。希尔伯特变换适用于分析非线性、非平稳信号分解且具有自适应性，Teager能量算子（TEO）是一种非线性算子，与希尔伯特变换相比，原理简单、运算量小，具有更好的实时性[11]。电缆行波測距的另一个关键问题是确定行波波速如何。行波波速是一个变化量，受多种因素影响，很难准确测定，因此测距误差较大[12]。综上所述，本文采用不受波速影响的双端测距算法以消除行波波速对测距精度的影响。

1 基于MEEMD与TEO行波波头检测方法

1.1 MEEMD原理

1.2 Teager能量算子

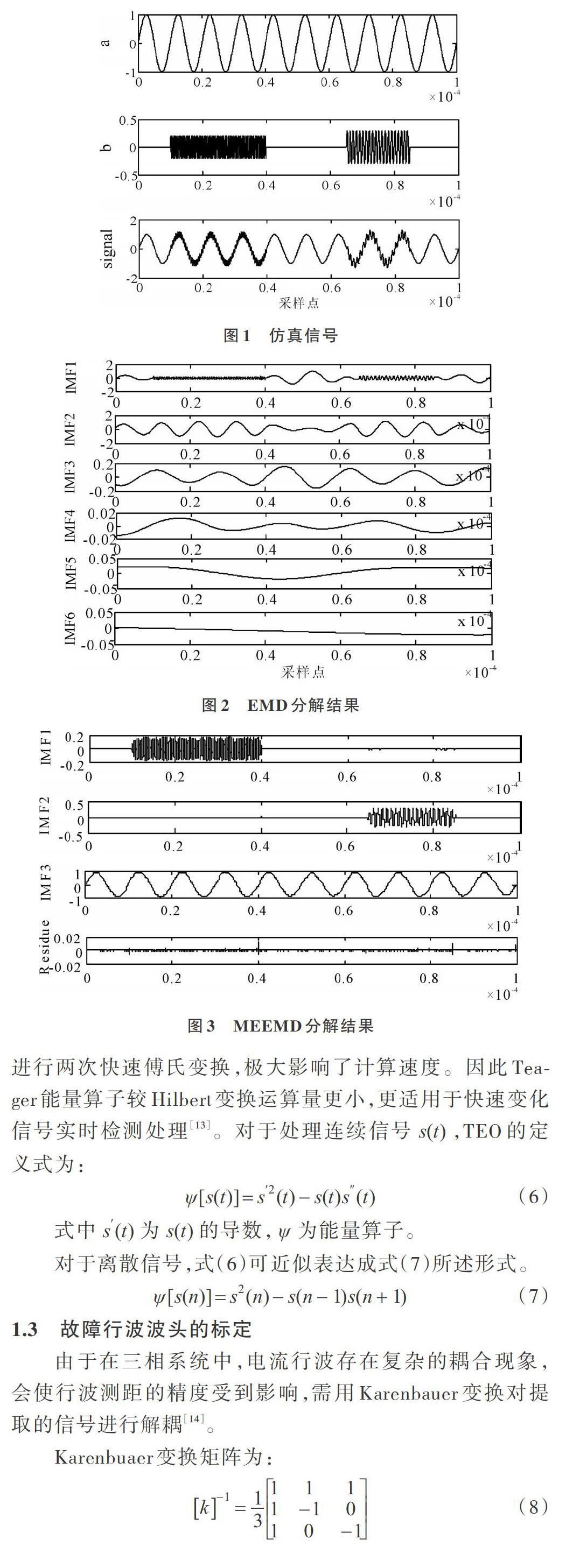
Teager能量算子是一种非线性能量算子，可以完整提取信号的瞬时频率与幅值，而Hilbert变换在变换过程中要进行两次快速傅氏变换，极大影响了计算速度。因此Teager能量算子较Hilbert变换运算量更小，更适用于快速变化信号实时检测处理[13]。对于处理连续信号[s（t）]，TEO的定义式为：

1.3 故障行波波头的标定

由于在三相系统中，电流行波存在复杂的耦合现象，会使行波测距的精度受到影响，需用Karenbauer变换对提取的信号进行解耦[14]。

故障行波波头标定的主要步骤包括：①利用Karenbauer变换解耦得到故障信号的线模分量;②对线模分量进行MEEMD分解，得到IMF分量;③取第一个IMF分量，计算Teager能量值，瞬时频谱上首个突变点即为波头到达位置。

2 双端行波测距算法

双端测距算法根据故障初始行波到达线路两端时间差的绝对值和行波波速求出故障点距离。双端测距公式为：

其中[l]为线路总长度，[v]为行波在线路的传播速度，[t1]、[t2]分别为故障行波到达线路两端的时刻。由公式（10）可知测距算法的精确度受线路实际长度、行波传播速度、波头到达线路两端时刻的影响。

电缆蛇形敷设基本结构如图4所示。电缆线路两点之间的地面水平距离与两点之间的电缆线路实际长度存在一定比例关系，并且导线长度随着温度变化也会发生均匀变化，工程中实际给出的线路长度为线路地面水平距离之和，如果按照给定的线路长度进行测量，会带来误差[15]。

在变化相同的温度下，电缆的变化是一个定值，因此其比值也是固定的，所以故障点到线路一端的地面水平距离[d]同故障点到该端实际电缆长度[d′]的比值近似于给定的线路长度[l]与电缆线路实际长度[l′]的比值。行波波速是一个不确定值，按照给定波速计算同样会增大误差，运用不受波速影响的双端测距算法能够进一步减小测距误差。

假设故障发生时刻为[t0]，则故障点到该端实际电缆长度[d′]为：

3 仿真验证

4 结语

本文针对传统Hilbert-Huang变换在电力电缆测距中存在的模态混叠问题，提出一种基于MEEMD和TEO的电力电缆测距方法，该方法消除了EMD模态混叠现象，基于电力电缆线路的实际情况，推导出不受波速影响的双端测距算法计算故障距离。以不同故障距离、不同过渡电阻进行仿真，结果表明，该方法相对传统Hilbert-Huang变换，测量精度高、耗时短且不受故障距离和过渡电阻影响，测距误差能达到工程实际要求。

参考文献：

[1] 杨军，伍咏红，江文波，等. 基于双端故障信息的高压电缆-架空线混和线路故障测距方法[J]. 电网技术，2015，34（1）：208-213.

[2] 黄忠棋. 采用行波固有频率的混和线路故障测距新方法[J]电力系统及其自动化学报，2015，27（11）：73-79.

[3] 覃剑，陈祥训，刘建超，等. 利用小波变换的双端行波测距新方法[J]. 中国电机工程学报，2000，20（8）：6-10.

[4] 王星海，许珉，谢志棠，等. 基于小波变换和自相关分析的电力电缆故障测距[J]. 继电器，2005，33（12）：32-35.

[5] 廖晓辉，赵肖健，梁恒娜. 一种基于Hilbert-Huang变换的電力电缆故障测距方法[J]电力系统保护与控制，2017，45（3）：20-25.

[6] 田书，寿好俊，尚鹏辉. 基于HHT的谐振接地配电网暂态量故障选线研究[J]. 测控技术，2017，36（3）：14-19.

[7] 黄诚惕. 希尔伯特-黄变换及其应用研究[D]. 成都：西南交通大学，2006.

[8] 张小丽. 基于希尔伯特-黄变换的输电线路故障行波定位与保护方法[D]. 长沙：长沙理工大学，2008.

[9] 田书，尚鹏辉，寿好俊. 基于EEMD的电缆故障测距方法仿真研究[J]. 测控技术，2016，35（11）：36-39.

[10] 郑旭，郝志勇，卢兆刚，等. 基于MEEMD的内燃机机体活塞敲击激励与燃烧爆发激励分离研究[J]. 震动与冲击，2012，31（6）：109-113.

[11] 夏欢. 基于智能信号分析的配电网故障定位方法的仿真研究[D]. 北京：华北电力大学，2015.

[12] 黄雄，王志华，尹项根，等. 高压输电线路行波测距的行波波速确定方法[J]电网技术，2004，28（19）：34-37.

[13] 郝勇奇，王倩，周士琼，等. 基于LMD与Teager能量算子的VSC-HVDC输电线路故障定位[J]电力系统保护与控制，2017，45（1）：81-88.

[14] 任艳霞. 电力电缆故障诊断与监测[D]. 北京：北京交通大学，2007.

[15] 高艳丰. 基于VMD和TEO的高压输电线路雷击故障测距研究[J]. 电工技术学报，2016，31（1）：24-33.

（责任编辑：江 艳）