基于矩阵填充理论的R-D算法

陈宇祺

摘 要：当被探测目标存在微动或者部件微动时，目标微动或其微动部件的回波与目标主体的回波叠加在一起，给成像处理带来影响，针对该问题提出一种基于矩阵填充的R-D算法。利用矩阵填充理论中的压缩感知对被干扰、扰动的观测信号进行重构和恢复，降低微多普勒带来的频带影响，从而提高SAR图像对比度。

关键词：SAR 矩阵填充;多普勒;压缩感知;R-D算法;微多普勒

DOI：10. 11907/rjdk. 182360

中图分类号：TP312文献标识码：A文章编号：1672-7800（2019）001-0086-05

Abstract： In view of the fact that the rigid object assumption is no longer satisfied when the target has fretting or fretting components.The echoes of the fretting or fretting components of the target are superimposed on the echoes of the main body of the target which brings many problems to the imaging processing. This paper proposes a matrix filling-based R-D algorithm which uses matrix filling theory to fill the pressure. In order to reduce the frequency band effect caused by micro-Doppler and improve the contrast of SAR image， the idea of shrinkage sensing is used to reconstruct and restore the disturbed and disturbed signals.

0 引言

合成孔徑雷达（Synthetic Aperture Radar， SAR）是一种成像雷达，用来对一般的雷达目标如飞机、舰船、导弹等进行成像，具有全天候工作能力。合成孔径雷达作为一种高分辨率成像雷达，原理是通过发射大带宽的脉冲信号获得高的距离分辨率，利用载机运动形成的合成孔径提高横向分辨率，得到目标的二维图像。

雷达向目标发射电磁波，电磁波经过反射后产生回波，被雷达接收机接收。当目标与雷达之间存在相对运动时，回波信号的载频会发生偏移，这个效应称为多普勒效应。当目标相对于雷达以恒定的速度运动时，多普勒频移的大小由雷达发射电磁波的波长和目标与雷达的相对速度决定，定量关系如下：

其中，[V]是目标与雷达的相对径向速度。当目标与雷达距离越来越远时，相对速度定义为正，[λ]为雷达发射信号的波长。当目标存在振动、旋转时，这些微动会对回波信号造成额外的频率调制，使多普勒中心周围出现旁瓣，这就是微多普勒效应[3]。

在SAR 成像中，目标一般近似为刚体目标。通过运动补偿，目标可以看作是转台目标，不同方位位置的散射中心相对于雷达具有不同的径向速度，导致回波具有不同的多普勒频率。当目标存在微动或者微动部件时，刚体假设不再满足，目标微动或微动部件的回波与目标主体的回波叠加，给成像处理带来诸多问题[1]：①微动的存在会对运动补偿精度产生影响;②微动造成的带宽展宽，经过方位向压缩微动部分散焦，产生方位向干扰条带[2]。所以，微多普勒抑制成为SAR成像的一个重要课题，本文采用矩阵填充理论对SAR成像产生的微多普勒进行抑制。

在经典的SAR成像算法中，R-D算法应用较多。但是 R-D算法同样存在距离、相位抖动问题，更易受到微动带来的多普勒效应的干扰，使SAR图像质量受到影响。

1961年，Gardner[6]的一篇报告里首次提到了喷气式飞机引擎的 JEM 调制现象，并且作了详细分析和研究。

1979年，Kleinman[7]的论文研究了线性振动目标的散射特性，之后研究人员对振动目标回波特征进行了深入研究，20世纪90 年代后开展了对雷达目标加速等非匀速运动对雷达回波的影响研究。1998 年，在激光雷达应用中观测到微多普勒现象，并首次提出微多普勒效应这一概念。美国国家海军实验室的 Victor将微多普勒概念引入到微波雷达中，并通过仿真和实测数据实验，证实了微多普勒效应的存在。在之后的研究中建立了目标典型微动形式的数学模型，分析了这些微动引起的微多普勒效应特性，提出了一种时频分析方法[8]。

国内微多普勒研究主要集中在微多普勒效应的应用，国防科技大学空间电子技术研究所陈行勇是第一个在该领域开展相关研究工作的，其通过仿真和实测数据实验，提出并验证了一些有效的参数估计以及目标识别方法。中国航天二院第23研究所发表了用于目标识别的微多普勒效应研究结果。在抑制成像中的微多普勒效应方面，研究人员也有成果发布。Xueru Bai等[10]提出基于复数经验模式分解（CEMD）的微多普勒效应提取方法，仿真和实测数据实验都取得了良好结果。

1 相关工作

矩阵填充指已知一个元素不完整的矩阵，对它进行填充重构出完整的矩阵。假设该矩阵是一个低秩矩阵，可以通过矩阵线性运算的一些结果将其转化成一个优化问题进行精确重构，是信号处理领域的研究热点之一。

（1）矩阵的低秩特性。类似于 CS 中原始信号和压缩感知矩阵必须分别满足稀疏性和 RIP 两个先验条件，而其原始矩阵和采样集的选择需要分别满足低秩和均匀随机采样两个条件。

（2）矩阵的非相干特性。将仿射秩最小问题（ARMP）的仿射受限等距特性与矩阵填充（MC）中的非相干特性结合起来，仿射受限等距特性是CS中RIP在MC中的推广，由于RIP研究已相对成熟，这必然加快矩阵填充理论的发展[15]。

2 矩阵填充理论

2.1 相关概念

2.1.1 相干度[24]

设[U]是[？n]的[r]维子空间，[PU]是在[U]上的正交投影，则[U]的相干度定义为：

2.1.2 不相干性

将模型转化为一个半正定规划问题，此方法需要函数的二阶信息，计算复杂度为[O（m6）]（其中[m]是矩阵维数），所以处理大规模问题时性能较差。参考压缩感知理论，提出大量的一阶快速算法，从而解决较大规模的矩阵填充问题[26]。

矩阵填充算法在于通过重构数据本征空间的低纬度信息得到被干扰的数据，从而优化传统R-D算法质量，这里的矩阵重建与机器视觉的压缩感知理论是一致的。

3 R-D算法仿真

使用矩阵填充框架进行螺旋桨飞机成像，在一维距离像上选取回波是关键一步。由于螺旋桨单元的回波幅度的闪烁特性，螺旋桨所在距离单元的谱线沿慢时间的幅度起伏要比只包含飞机目标稳定散射点大得多，因此将这几个距离单元谱线幅度相加，找到和幅度最小的一些回波，这些回波所对应的行即是单位样值函数[φk=δ（n-k）]中的k值，依照此方法即可得到该算法的观测矩阵。

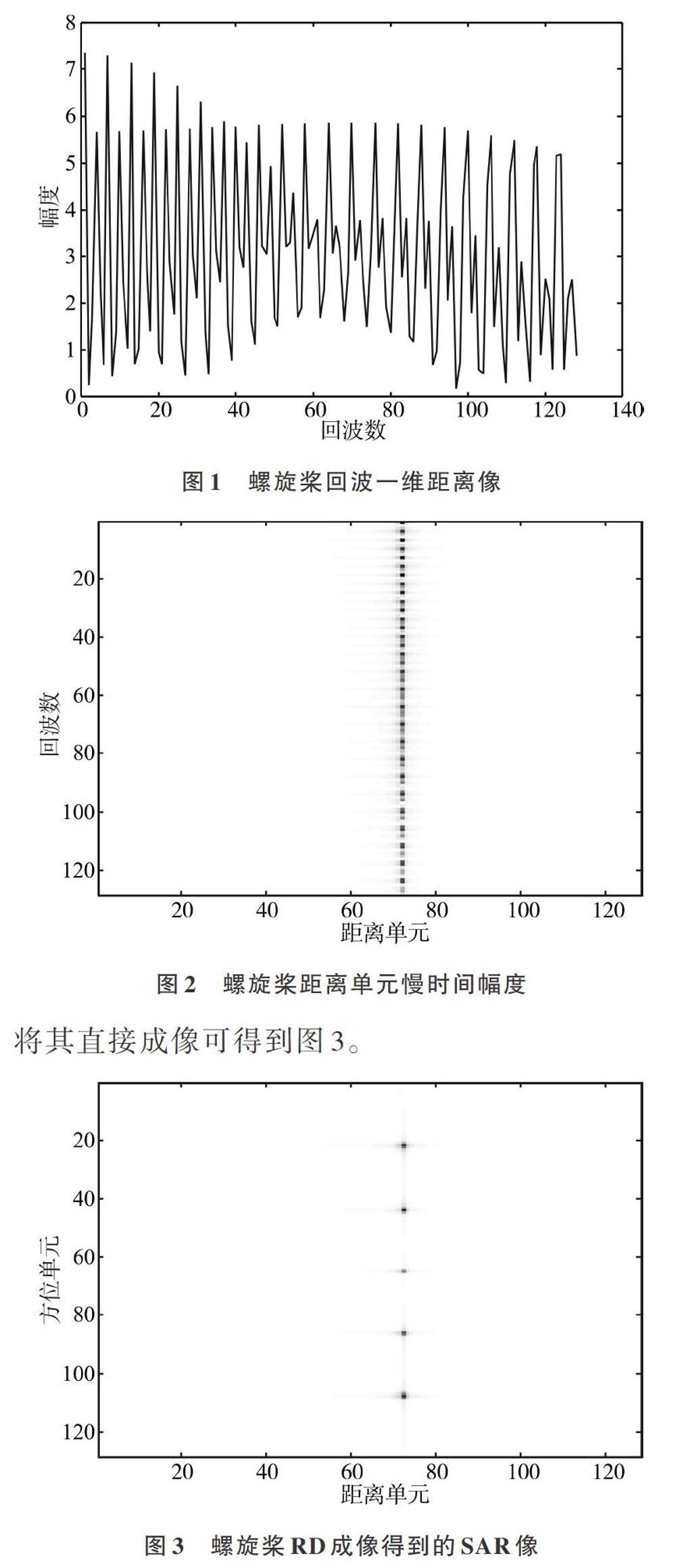
通过实验对上面的分析进行验证。首先单独对螺旋桨进行仿真，设雷达发射线性调频脉冲发射载波频率10GHz，则波长为3cm，脉冲重复频率为500Hz，脉冲宽度为25.6us，带宽为400MHz。以雷达为原点建立空间坐标系，螺旋桨的旋转中心位于空间坐标系的（200，10 000，200），旋转轴与y轴平行。螺旋桨桨叶长1.2m，桨叶数N=4，fp=  1 255r/min，共积累0.256s，得到128个回波。假设飞机静止不动，经过计算得到一维距离如图1所示。选取螺旋桨所在的距离单元，按照慢时间对其一维回波幅度进行显示，得到图2。

以雷达所在位置为原点建立空间坐标系[（ξ1，ξ2，ξ3）]，以飞机旋转中心为原点建立目标坐标系[（Xt，Yt，Zt）]，然后以螺旋桨的旋转中心为原点建立螺旋桨坐标系[（Xp，Yp，Zp）]。飞机的转动有3种形式，分别以绕[Xt，Yt，Zt]轴的俯仰、滚动、偏航来描述。一般螺旋桨飞机的航行姿态比较稳定，假设飞机只作偏航转动，在相干积累时间内转动的角度为[φ（t）]。螺旋桨自身以角速度[ωp]绕[Yp]轴作逆时针旋转，其中心在目标坐标系上的坐标为[（xa，ya，za）]。P为螺旋桨上任一散射点，其在螺旋桨坐标系中的初始坐标为[（-rcosθ0，0，rsinθ0）]，其中r为散射点相对于螺旋桨中心的距离，[θ0]为其与中心的连线与x轴的初始夹角，其瞬时坐标为[[-rcos（θ0+ωpt），0，rsin（θ0+ωpt）]]，转换到目标坐标系中，坐标为[[xa-rcosθ（t），ya，za+rsinθ（t）]]。飞机机身散射点在目标坐标系的坐标为[xt，yt，zt]，各个散射点沿目标旋转中心转动后，由旋转矩阵

将飞机和螺旋桨在目标坐标系的坐标转换到空间坐标系中，得到螺旋桨散射点与雷达之间瞬时距离Rp（t）和Rt（t）。仿真所使用的雷达波形参数和螺旋桨形式都与上一部分的参数相同，飞机目标取5个散射点，规定机身平行于y轴，机头冲向y轴负方向时的姿态为转角0°的姿态。设定飞机存在两个螺旋桨，螺旋桨参数也与第一部分相同，设定螺旋桨旋转中心在目标坐标系中的坐标为（-5，-5，0），（5，-5，0），飞机的旋转中心在空间坐标系中的坐标为（200，10 000，200），相干积累时间内接收256个回波，飞机进行匀速偏航转动，转动角度使其方位分辨率与距离分辨率相同。在距离域回波中同样采256个点。如果飞机初始转角为0°，此时两个螺旋桨在空间坐标系中的y坐标相同。由于目标尺寸远小于雷达到目标的距离，因此两个螺旋桨的回波基本集中在少数几个距离单元中。按照最基本的R-D成像方法对该目标进行成像，得到其一维距离像和SAR像如图5和图6所示，其SAR像的对比度为20.865 1。

SAR像中，螺旋桨回波的多普勒展宽对于二维成像造成一定干扰。从一维距离像可以看出，螺旋桨散射点的起伏要强于机身的散射点，故可以采用一定的方法将螺旋桨散射点的距离谱线提取出来。本算法采用方差法，首先提取出一维距离像的实包络，然后对每个距离单元的实包络分别求方差，提取出方差最大的几个距离单元。经过计算，得到方差最大的3个距离单元分别是115、116和117，对比图1，确实是螺旋桨回波所在距离单元，证明该方法在仿真验证中是有效的。提取出相应的距离谱线以后，对这几个距离单元的实包络按照慢时间分别求和，可以求出对应的和幅度，挑选出这几个距离单元中和幅度较小的64个回波，回波选取实现使用单位样值函数组成的观测矩阵。将傅里叶基作为稀疏基，对这些距离单元利用基追踪算法将高分辨图像重构出来。对于其它距离单元直接进行IFFT，然后将这些距离单元排列起来，即可得到微多普勒抑制的SAR图像，如图7所示。图像对比度为35.252 2。

可以看出，压缩感知框架下的成像确实比直接进行RD算法的聚焦效果要好得多，而且对螺旋桨回波也有较好抑制。虽然不能完全将其去除，但对于飞机目标识别的影响已经可以忽略。通过该方法既能减少后续处理的数据量，使雷达载荷降低，又能够保证成像效果，同时还能抑制螺旋桨对SAR成像的影响。

最后利用Ann-26飞机实测数据对该算法进行验证，实测数据进行运动补偿后得到的一维距离像和SAR像如圖8和图9所示，图中SAR图像的对比度为17.674 8。可以看到Ann-26飞机由于螺旋桨的存在产生了微多普勒的条带干扰，使得RD成像质量下降，按照本文算法进行压缩感知处理，选取24个对比度最大的单元，保留128个回波，得到最终的结果如图10所示。可以看到螺旋桨回波得到了有效抑制，保证了飞机主体目标的成像质量，其对比度为24.118 0。

4 结语

由仿真结果可知，基于矩阵填充（压缩感知）理论的R-D算法能够对螺旋桨回波形成比较好的抑制，虽然不能完全将其去除，但对于飞机目标识别的影响已经可以忽略不计。通过该方法既能减少后续处理的数据量，使雷达载荷降低，又能保证成像效果。

参考文献：

[1]   CHEN V C. Analysis of radar micro-Doppler signature with time-frequency transforms[C]. Proceedings of the 10th IEEE Workshop on Statistical Signal and Array Processing， 2000： 463-466.

[2]   CHEN V C， LI F，HO S S，et al. Analysis of micro-Doppler signatures[J]. IEEE Proceedings of Radar Sonar Navigation，2003，150（4）：201-207.

[3]   CHEN V C， LI F， HO S S， et al. Micro-Doppler effect in radar： phenomenon， model， and simulation study[J]. IEEE Transactions on Aerospace & Electronic Systems， 2006， 42（1）：2-21.

[4]   CHEN V C，LING H. Time-frequency transforms for radar imaging and signal analysis[J]. Microwave Joural，2002（1）：185-189.

[5]   THAYAPARAN T，ABROL S， RISEBOROUGH E， et al. Analysis of radar micro-Doppler signatures from experimental helicopter and human data[J]. IET Radar Sonar Navigation，2007，1（4）：289-299.

[6]   THAYAPARAN T，STANKOVIC L，DJUROVIC I，et al. Intelligent target recognition using micro-Doppler radar signatures[J]. Proceedings of SPIE - The International Society for Optical Engineering，2009（6）：7308-7321.

[7]   KLEINMAN R E，MACK R B. Scattering by linearly vibrating objects[J]. IEEE Transactions on Antennas & Propagation，1979，27（3）：344-352.

[8]   CHEN V C. Micro-Doppler effect of micromotion dynamics： a review[J]. Proceedings of SPIE - The International Society for Optical Engineering， 2003（5102）：240-249.

[9]   LI B，WAN J W，YAO K Z，et al. ISAR based on micro-Doppler analysis and chirplet parameter separation[C]. Synthetic Aperture Radar， 2007. Apsar 2007. Asian and Pacific Conference on，2007：379-384.

[10] 張琳，盛卫星，马晓峰. 基于微多普勒效应的雷达目标识别算法[J]. 现代雷达，2007，29（12）：35-39.

[11] CANDES E J，ROMBERG J，TAO T. Robust uncertainty principles： exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory， 2006， 52（2）：489-509.

[12] CANDèS E，ROMBERG J. Sparsity and incoherence in compressive sampling[J]. Inverse Problems，2006， 23（3）：969-985.

[13] 娄永杰. ISAR成像中微多普勒效应研究[D]. 哈尔滨：哈尔滨工业大学，2009.

[14] CANDES E，RUDELSON M，TAO T，et al. Error correction via linear programming[C]. Foundations of Computer Science，2005. FOCS 2005. IEEE Symposium on. IEEE， 2005：295-308.

[15] CANDèS E J，RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics， 2008， 9（6）：717-772.

[16] CAI J F，CAND S，E J，et al. A singular value thresholding algorithm for matrix completion[J]. Siam Journal on Optimization，2008，20（4）：1956-1982.

[17] 武棟，曾理. 低秩矩阵复原技术及在CT图像重建中的应用[C]. 中国体视学与图像分析学术会议，2015.

[18] 姚波旭. 基于低秩矩阵分解的非局部稀疏模型图像去噪方法研究[D]. 西安：西安电子科技大学， 2014.

[19] 刘新艳. 基于稀疏低秩矩阵的有噪图像修复方法研究[D].天津：河北工业大学， 2013.

[20] 周密，宋占杰. 基于稀疏与低秩矩阵分解的视频背景建模[J]. 计算机应用研究，2015，32（10）：3175-3178.

[21] 陈行勇，刘永祥，黎湘，等. 微多普勒分析和参数估计[J]. 红外与毫米波学报，2006（25）：360-363.

[22] THAYAPARAN T，STANKOVIC L，DJUROVIC I，et al. Intelligent target recognition using micro-doppler radar signatures[J]. Proceedings of SPIE - The International Society for Optical Engineering， 2009（3）：7308-7311.

[23] SANTI F，BUCCIARELLI M，PASTINA D. Target rotation motion estimation from distributed ISAR data[C]. 2012 IEEE Radar Conference，2012： 659-664.

[24] TSAIG Y，DONOHO D L. Extensions of compressed sensing[J]. Signal Processing，2006，86（3）： 549-571.

[25] CANDES E J. The power of convex relaxation： the surprising stories of matrix completion and compressed sensing[C]. Acm-Siam Symposium on Discrete Algorithms，2010：1321-1321.

[26] THE POWER OF CONVEX RELAXATION.The surprising stories of matrix completion and compressed sensing[EB/OL]. http：//www.doc88.com/p-6951579321353.html.

[27] CHO J， KIM D， ROHE K. Intelligent initialization and adaptive thresholding for iterative matrix completion[C]. Some Statistical and Algorithmic Theory for Adaptive-Impute 2016.

[28] 彭义刚，索津莉，戴琼海，等. 从压缩传感到低秩矩阵恢复：理论与应用[J]. 自动化学报，2013，39（7）：981-994.

[29] 史加荣，郑秀云，魏宗田，等. 低秩矩阵恢复算法综述[J]. 计算机应用研究，2013，30（6）：1601-1605.

[30] 陈晓璇，齐春. 基于低秩矩阵恢复和联合学习的图像超分辨率重建[J]. 计算机学报，2014，37（6）：1372-1379.

[31] 杨敏，安振英. 基于低秩矩阵恢复的视频背景建模[J]. 南京邮电大学学报：自然科学版，2013，33（2）：86-89.

[32] 吴君钦，邬亮. 新融合小波变换与低秩矩阵恢复图像去噪算法[J]. 电视技术， 2016， 40（3）：17-21.

[33] 李军，邢孟道，张磊，等. 一种高分辨的稀疏SAR成像方法[J]. 西安电子科技大学学报：自然科学版，2010（37）：441-446.

（责任编辑：杜能钢）