用差异演化-粒子群混合算法确定含水层参数

段国荣，刘元会

(长安大学 理学院，陕西 西安 710064)

0 引 言

在中国工业快速发展的进程中，水资源问题逐渐增多，地下水是水资源的重要组成部分，地下水资源的评价及开发利用就变得特别重要。含水层参数是进行地下水资源评价和开发利用的基础数据。开发利用地下水资源时，往往会遇到含水层具有直线供水边界的情况。标准曲线配线法[1]，时间定律法(Law of Times)和拐点法(Method of Inflection Point)[2]，非线性最小二乘法[3-4]，线性回归法[5]，Su shil K.S.方法[6-7]，直线图解法[8]和割离井法[9-10]等是分析直线供水边界含水层抽水试验数据的传统方法，但此类方法在实际应用中受到一定的限制。近年来，人们广泛使用智能优化算法来分析抽水试验数据，求解含水层参数，例如粒子群优化算法[11]，混沌人工鱼群混合算法[12]，遗传算法[13]，改进粒子群算法[14]，单纯形探索法[15]，单纯形差分进化混合算法[16]，混沌粒子群优化算法[17]和单纯形-粒子群混合算法[18]等方法。郭建青，李彦等将粒子群优化算法[11]应用于确定含水层参数，但该算法对粒子数目的大小依赖性很强。袁帆，刘元会等利用单纯形-粒子群混合算法[18]计算含水层参数的问题，但计算结果精度不高，且粒子数目的大小和待估参数取值范围对算法的收敛性有较大的影响。粒子群优化算法[11]操作简单且易实现，但种群多样性的缺失使其易陷入局部最优。因此，本研究对粒子群优化算法(PSO算法)进行改进，提供一种差异演化-粒子群混合算法(DE-PSO算法)。将差异演化-粒子群混合算法用于分析直线供水边界条件下含水层的抽水试验数据，求解含水层参数，计算观测孔与虚拟映射井之间的距离。本研究重点讨论了该算法的可靠性和有效性，并就待估参数取值范围对算法收敛性的影响进行数值实验分析。

1 优化算法简介

1.1 DE-PSO算法的思想

PSO算法在迭代后期由于种群多样性的下降存在收敛速度慢，精度差，且易陷入局部最优等问题，利用DE算法[19-21]中的3种遗传操作，即变异操作，交叉操作和选择操作，变异粒子中各个体的历史最优位置，不仅能使种群保持一定的多样性，进而避免出现早熟或停滞的现象，而且能保持PSO算法迭代前期收敛速度快的优点。本研究引入聚集度因子[22]来确定粒子个体历史最优位置是否需要进行变异

(1)

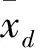
1.2 DE-PSO算法的步骤

步骤1：初始化算法的相关参数；确定粒子个数N，搜索空间维度D，最大迭代次数gen，最优累计次数K[23]，各粒子的初始位置及初始速度、搜索空间的上下限、缩放因子F，交叉概率CR，初始化循环迭代次数t和最优累计次数k，聚集度因子Fa，收敛精度e1以及计算相似度e2[23].

步骤2：计算初始种群中每个粒子的适应度值，保存粒子局部和全局最优位置，最优值。

步骤3：若当前迭代次数小于最大迭代次数gen且当前的最优累计次数k小于最优累计次数K，则进入循环，否则输出最优结果。

步骤4：更新每个粒子的速度和位置，且进行粒子个体最优更新及群体最优更新。

步骤5：计算粒子的聚集度因子Fa，若Fa大于所给定的阈值，则进入步骤6，否则返回步骤4.

步骤6：利用DE算法中的变异、交叉、选择等遗传操作，变异粒子中各个体的历史最优位置，并更新粒子历史最优位置。

步骤7：如果全局最优解小于e1且全局最优解的误差小于相似度e2，则k=k+1，否则返回步骤3继续执行。

步骤8：输出结果。

2 目标函数与控制条件

2.1 降深表达式

由地下水动力学[24-25]中的迭加原理可知，含水层中任一位置的降深可以由2部分迭加得到，即在直线供水边界条件下，虚拟映射注水井注水和抽水实井抽水分别在该位置产生降深的叠加。虚拟映射注水井、抽水实井和直线供水边界的位置关系[5]，如图1所示。

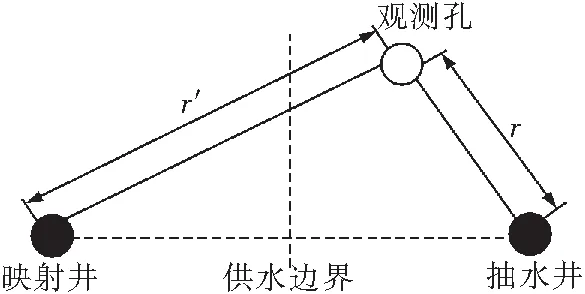
图1 直线供水边界条件下抽水实井和虚拟映射注水井的位置关系Fig.1 Location relationship between the pumping well and the virtual mapping injection well in linear pervious boundary

该情况下，含水层中任一位置的降深表达式[26]如下

s=s1+s2=[w(u1)-w(u2)]Q/4πT

(2)

式中Q为抽水流量，L3/T1；T为含水层的导水系数，L2/T2；s1为直线供水边界条件下实井抽水引起的降深，L；s2为直线供水边界条件下虚拟映射注水井引起的降深，L；w(u1)和w(u2)分别为相应的抽水实井和虚拟映射注水井的井函数，无量纲，其表达式分别为

(3)

其中无量纲时间参量u1和u2的表达式分别为

(4)

式中t为抽水持续时间,T；S为储水系数，无量纲；r为抽水实井与观测井的距离，L；r′为虚拟映射井与观测井的距离，L.

③有法不依、执法不严的问题比较突出。由于管理体制不顺，违反《塔里木河水资源管理条例》、自治区批准的水量分配方案、水量调度管理办法，不执行水调指令，抢占、挤占生态水，不按塔里木河规划确定的输水目标向塔里木河输水的现象时有发生。塔里木河干流水权及生态用水水权得不到依法保护，塔管局由于现行的管理权限所限，难以依法进行处罚。

由式(3)可知，在计算水位降深值时，需要对井函数进行广义积分求解。采用R.Srivastava给出的近似表达式[27]进行计算

W(u)=-Inu+a0+a1u+a2u2+a3u3+a4u4+a5u5,u≤1

(5)

(6)

式中a0=-0.577 72，a1=0.999 99，a2=-0.249 1，a3=-0.055 19，a4=-0.009 76，a5=0.001 08，b0=0.267 77，b1=8.634 76，b2=18.059 02，b3=3.958 50，c0=3.958 50，c1=21.099 65，c2=25.632 96，c3=9.573 32.

2.2 目标函数的构成

采用DE-PSO算法求解含水层参数时，待估参数向量θ=(T,S,r′)应满足降深观测值与计算值的方差达到最小，构造如下目标函数

(7)

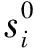
2.3 算法参数控制

聚集度因子Fa∈[0,2]，根据多次试验结果，本研究选取Fa的阈值Fa=1.3，交叉概率CR∈[0,1]，缩放因子F∈[0,2]，粒子数目维度N=20，最大迭代次数gen=200，根据文献[28],选取含水层导水系数T∈[2.5,3.5] m2/min，储水系数S∈[0.050,0.070]，观测井到虚拟映射井的距离r′∈[100,130] m，取e1=5×10-5，e2=10-9，K=10.

3 算例

3.1 不同方法计算结果的比较

表2中给出了DE-PSO算法和相关文献中的其他方法对含水层参数的计算结果。

从表2可知，DE-PSO算法估计含水层参数值及观测井与虚拟映射井之间的距离与其他方法接近，且由该算法求得的φ(θ)精度高于其他方法，因此，DE-PSO算法所求结果是可靠的。

3.2 算法的有效性

图2表示的是DE-PSO算法的程序运行100次目标函数值的分布情况。从图2能够看出，在DE-PSO算法的程序运行100次的过程中，有91次成功，其收敛率达到91%.由此可知，DE-PSO算法的收敛率较高，具有高效性。因此，利用DE-PSO算法能有效地估计含水层参数。

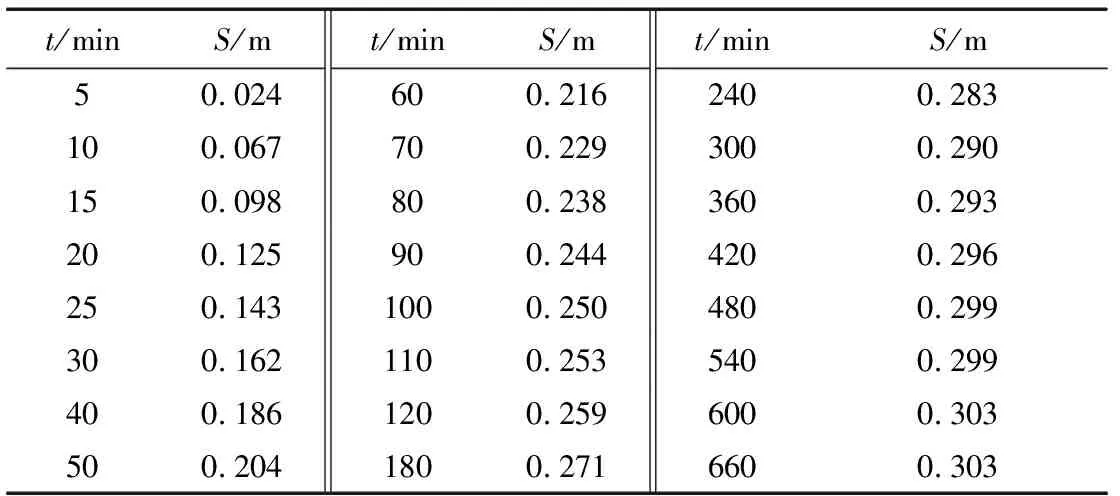
表1 原始抽水试验数据

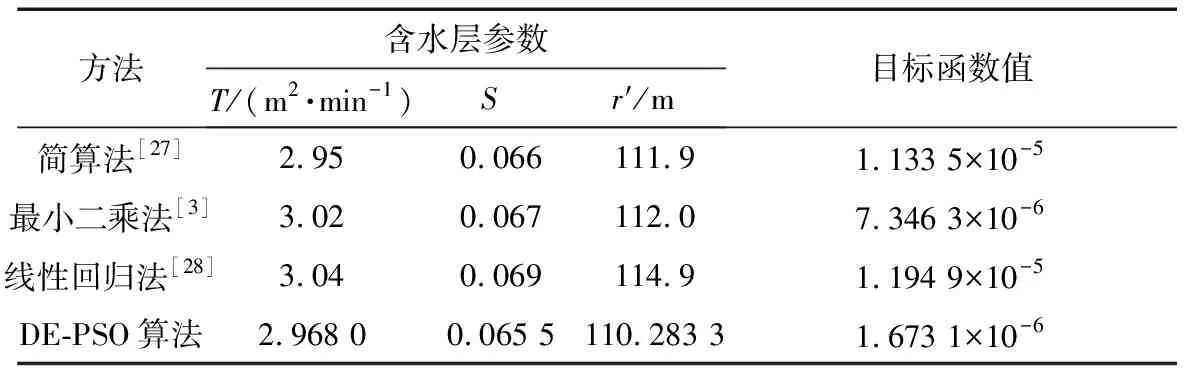
表2 不同方法的计算结果

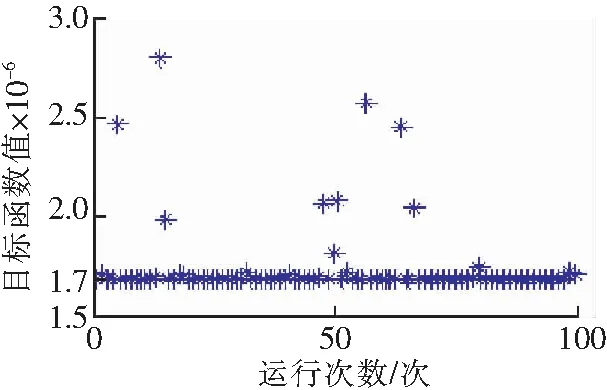
图2 DE-PSO算法运行100次目标函数值分布Fig.2 Distribution of the objective function value after 100 runs of DE-PSO algorithm

3.3 算法的稳定性

表3是在其他条件不变，待估参数取值范围的上限扩大到原来的2，4，8，10，12和14倍的情况下，利用DE-PSO算法求得含水层参数及观测井与虚拟映射井之间距离的估计值。由表中信息可知，随着待估参数范围的增大，DE-PSO算法具有很好的收敛性，当待估参数取值范围的上限扩大到原来的14倍时，收敛率高达97%，且得到目标函数值基本一致，即DE-PSO算法对初值选取的敏感性低，寻优能力强，稳定性好。

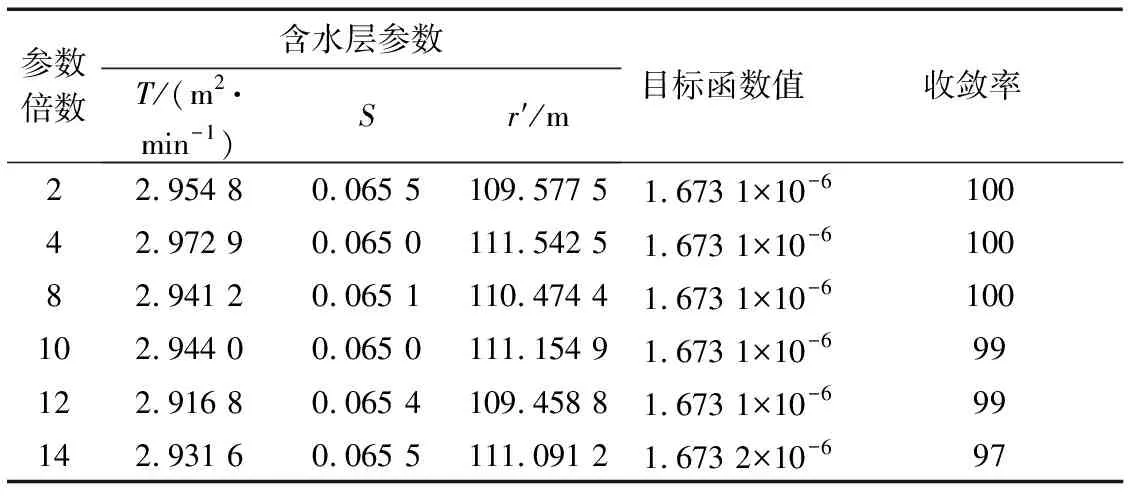
表3 不同参数取值范围下的计算结果

4 结 论

1)DE-PSO算法得到的目标函数值φ(θ)精度高于其他方法。

2)估计含水层参数时具有较好的收敛性，具有较高的精度。

3)待估参数初始取值范围的放宽对DE-PSO算法的收敛性影响较小，即DE-PSO算法对初始取值范围选取的敏感性低，寻优能力强，稳定性好。因此，DE-PSO算法是分析抽水试验数据，求解含水层参数和计算观测孔与虚拟映射井之间距离的有效方法。