亚纯函数及其微分多项式IM分担小函数
2019-06-06王汉杰王新利
上海理工大学学报 2019年2期
王汉杰,王新利
(上海理工大学 理学院,上海 200093)
1 问题的提出
使用Nevanlinna值分布理论中的标准记号[1-3],如表示型的量,其中,为上的一个线性测度有穷的集合。记亚纯函数的微分多项式为:其中,为f的小函数,满足
1995年,方明亮[4]引入了几乎分担的概念。
定义1[4]和为2个非常数的亚纯函数,其中,。表示相应的幂指量。记

1977年,仪洪勋等[1]证明了定理1。
定理1[5]设是非常数整函数,如果和分担2个判别的有穷复数,那么,。
1996年,Brück[6]提出了著名的猜想定理2。

1998 年 , Gundersen 等[7]研究了有穷级的情况,改进了定理 2,证明了定理 3。

由此考虑:一方面,将有穷级的限制条件去掉,是否有类似结论;另一方面,将分担有限值推广到分担小函数,定理3的结论是否成立。
2003年,Yu[8]回答这一问题,证明了定理4和定理5。

2006年,刘礼培等[9]将定理4和定理5中的推广为,将定理4中的“和没 有公共极点”这个条件去掉,并减弱了亏量条件,进一步改进了定理4和定理5,证明了定理6和定理7。


在此基础上,本文考虑将定理6和定理7中的CM分担弱化为IM分担,将定理7中的“和没 有同级的极点”去掉,从而得到了定理8和定理9。

2 一些引理


3 定理8的证明
现证明定理8。
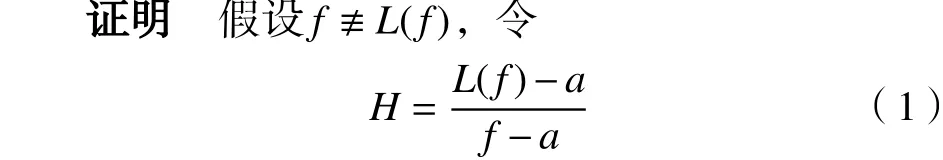
现分2种情形讨论。

由第二基本定理、引理2和引理3可得,
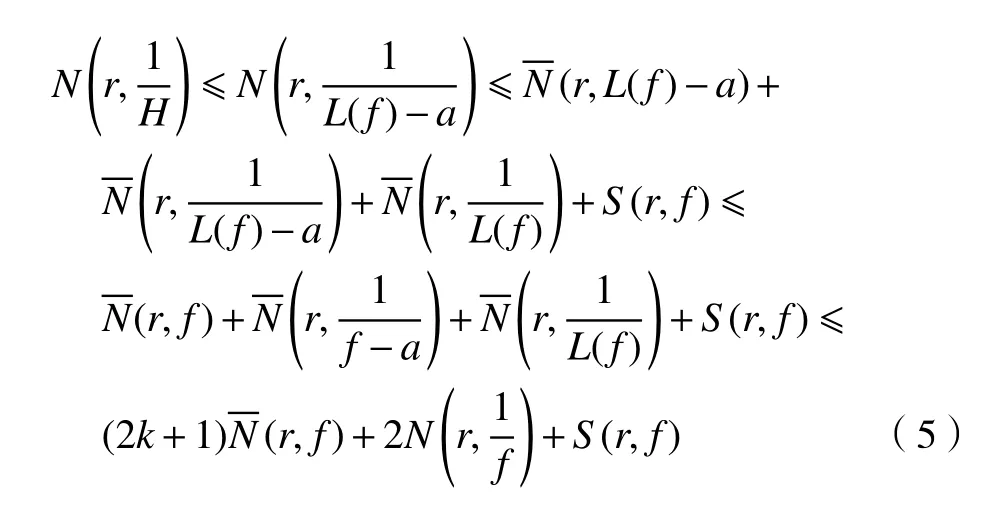
由式(2)和式(3)可得,
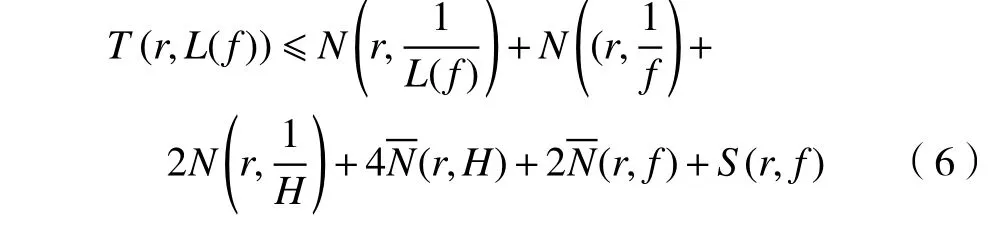
将引理2代入式(6)可得,

再区分3种情况。
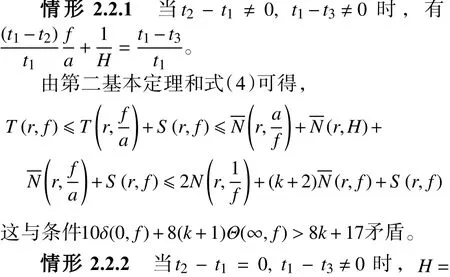
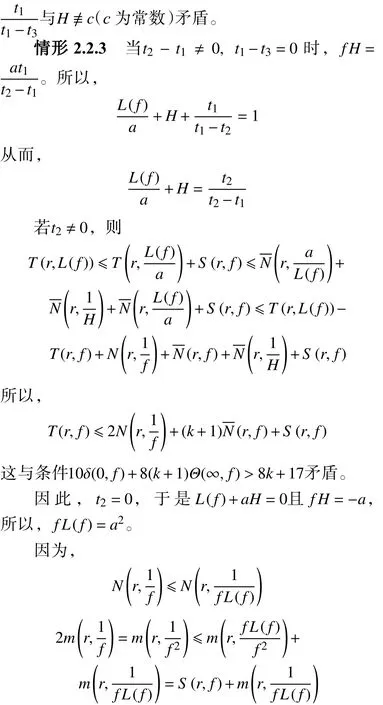

矛盾。因此,假设不成立,即 f≡L(f) 。定理8证毕。
4 定理9的证明
当 f (z)为非常数整函数,显然, Θ (∞,f)=1,由定理8的证明可得,若 f -a 和 L (f)-a分担0 IM,δ(0,f)> 9, f ≡L(f)。定理9证毕。
