求解广义分配问题的拉格朗日蝙蝠算法
2019-06-06万晓琼张惠珍赵玉苹
万晓琼,张惠珍,赵玉苹
(1. 上海理工大学 管理学院,上海 200093;2. 国网上海市电力公司 物资公司,上海 200235)
广义分配问题(generalized assignment problem,GAP)[1]是将给定的工作分配给有限定资源量的代理器来完成,以消耗最小的成本或取得最大利润为目标,是经典的组合优化问题。GAP在实际生活中具有广泛的应用,许多领域的容量约束问题都可以被抽象为GAP算例进行求解,如机器调度问题、有容量设施选址问题、供应链问题及车辆路径问题等。
GAP在理论和应用价值上的意义引起了国内外学者的极大关注,多种算法被用来求解此问题,这些算法大致可以归为3类:近似算法[2-3]、精确算法[4-6]和智能优化算法。由于GAP的复杂性,近似算法和精确算法对于求解大规模问题具有局限性,这促使了智能优化算法的广泛应用,如Bai等[7]采用粒子群算法(PSO)求解两阶段模糊GAP;Tapkan等[8]在蜂群算法中引入多种模糊排序方式用于解决模糊多目标GAP;Liu等[9]提出一种可扩展并行遗传算法(GA)求解GAP问题;Laguna等[10]在禁忌搜索算法(TS)中利用斥链定义邻域,并用其求解多级GAP。它们在解决组合优化问题时取得了一定的成果,同时也显现出单一智能优化算法的一系列缺点,如容易陷入局部最优解、稳定性差等。为了克服这些缺点,以及获得更精确的解,运用混合智能优化算法解决GAP问题得到长足的发展,如吴良杰等[11]将禁忌搜索算法作为蚁群算法的局部搜索策略,提出了混合算法,有效地解决GAP;Chen等[12]结合小生境遗传算法与蚁群算法,并建立蚂蚁搜索的禁忌规则,提出了小生境遗传蚂蚁算法来求解GAP;Osman[13]将禁忌搜索算法与模拟退火算法相结合,用于求解GAP。
本文运用蝙蝠算法(BA)[14]融合拉格朗日松弛算法(LR)[15-16]来解决基本GAP。该算法利用蝙蝠算法产生GAP最优解的上界,采用拉格朗日松弛算法求出GAP最优解的下界,两者结合,逐渐逼近GAP的最优解。
1 广义分配问题
GAP可以描述为:将n个相互独立的工作分配给m个有限定资源量的代理器,一个工作只能由一个代理器服务,一个代理器可以服务多个工作,且代理器完成工作所需的总资源量不能超过自身的限制。GAP的数学模型可表述为
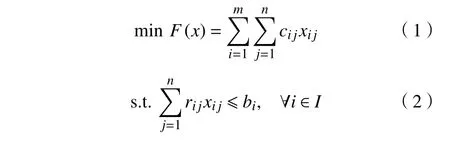

2 蝙蝠算法
蝙蝠算法最早由剑桥大学的Yang于2010年提出,是一种基于微型蝙蝠群体回声定位行为的搜索全局近似解的智能优化算法。蝙蝠个体是蝙蝠算法的基本单元,它们通过口腔或者鼻腔将从喉部产生的超声波发射出去,然后依据发出超声波和接收到回音之间的时差、到达两耳之间的不同强度、回声定位波形的变化来判断猎物或障碍物的距离、方位以及性质,从而制定捕捉猎物和躲避障碍物的计划,同时也使得蝙蝠即使在黑暗中也能找到位于裂缝中的栖息地。蝙蝠算法最早被用来解决连续问题,近几年有学者利用它来解决离散问题,例如,旅行商问题[17]、车辆路径问题[18]及背包问题[19]等。
本文尝试运用蝙蝠算法来解决基本GAP问题。在求解过程中,假设蝙蝠群体随机散布于d维搜索空间下,一个蝙蝠对应GAP问题的一个解,GAP问题的目标函数决定蝙蝠的适应度值,蝙蝠群体的其他个体通过调整超声波的响度、脉冲发射率来追随当前群体中的最优蝙蝠在解空间中进行搜索,从而使蝙蝠群体在求解空间中的运动由无序演变为有序,直至达到满意解。
2.1 求解GAP问题的蝙蝠算法
由于GAP问题的特点,基础的蝙蝠算法已不适用。本文在不改变蝙蝠算法原有概念和结构的基础上,引入单点基因换位算子建立全新的速度、位置以及局部搜索更新规则,称之为离散蝙蝠算法(discrete bat algorithm,DBA)。现从蝙蝠位置初始编码、蝙蝠位置和速度更新、局部更新以及音量和脉冲的更新这4个方面来介绍离散蝙蝠算法。
2.1.1 蝙蝠位置初始编码蝙蝠算法中蝙蝠的位置编码代表GAP的可行解。设蝙蝠种群大小为s,第i只蝙蝠的速度为vi,初始位置为xi,迭代次数N。现介绍第i只蝙蝠个体初始位置编码方式。
c. 从θi1开始进行分配,分配方式:将给定的代理器服务该工作时消耗的资源量按升序排列,从中随机选取前两个代理器中的任一个为其服务,若选中的代理器为w,则记,依次进行,直至全部工作分配完毕。
d. 若此时有代理器消耗的总资源量超出自身资源限制,则通过以下方式进行调整:搜索超出资源限制的代理器服务的工作,并计算代理器完成该工作时消耗单位资源花费的成本,将最大P值对应的工作重新分配给剩余资源量足够且花费成本最小的代理器。
2.1.2 蝙蝠速度和位置更新

式中:x*表示当前最优解,它是通过比较(当前整)个蝙蝠种群对应的适应度值而得到;指和x*之间的汉明距离,具体为第i只蝙蝠在第t-1时刻位置编码较最优蝙蝠位置编码对应位不同的个数。例如,可以看出,在,x*中工作1,4,5均被分配给1,2,1代理器,而工作2,3分配给不同的代理器,则此时=2。
蝙蝠的位置更新采用单点基因换位算子,即在蝙蝠原位置编码的基础上随机选取2个编码位置进行交换,换位后的位置编码对应的适应度值变优且符合约束条件时更新编码,直至共进行vit次单点基因换位,位置更新结束。以m=3,n=7为例,随机选取的2个编码位置为2和5,则单点基因换位的方式如图1所示。
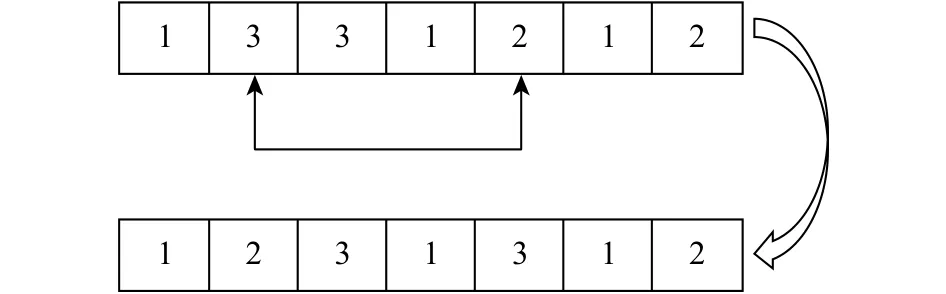
图1 单点基因换位方式Fig.1 Single point gene translocation
2.1.3 局部更新
类似于现存的其他智能优化算法,蝙蝠算法也可以进行局部搜索行为,且相对于其他算法,蝙蝠算法可以通过比较脉冲发生率ri和随机数的大小,实现对全局搜索和局部搜索之间转换的动态控制。
当随机函数rand>ri时,在当前最优解集中选择一个最优蝙蝠,进行随机游走,产生局部新解。游走方式同样采用单点基因换位,具体是在当前最优解集中选择一个最优蝙蝠,在该蝙蝠原有的位置编码的基础上进行一次单点基因换位,更新后的位置编码对应的适应度值变优且在符合约束条件时更新编码。
2.1.4 蝙蝠音量和脉冲发生率的更新
在蝙蝠接近猎物的过程中,声波音量逐渐降低,同时脉冲发生率逐渐提高。音量Ait和脉冲发生率rit的更新公式为

式中:α为音量衰减系数;γ为脉冲发生率增加系数。对任意 0<α<1,γ>0,可以看出逐渐接近最大脉冲发生率。
2.2 求解GAP问题的蝙蝠算法设计
通过上文方式进行基础蝙蝠算法的改造,设计出的全新求解GAP问题的蝙蝠算法的具体步骤如下:
步骤 1 初始化蝙蝠种群。蝙蝠种群个数为s,第i只蝙蝠初始位置为xi,速度为vi,音量为Ai0,脉冲发生率为ri0,迭代次数N。
步骤 2 运用式(5)以及单基因换位算子进行蝙蝠速度和位置的更新。
步骤 3 若rand>ri,进行局部搜索。
步骤 4 若rand<Ai且,接受这个新解。
步骤 5 根据式(6)和式(7)进行蝙蝠脉冲发生率和音量更新。
步骤 6 排列蝙蝠并找到当前最优蝙蝠x*。
N′=N′+1
步骤 7 ,若 ,则结束搜索并输出结果;否则,转步骤2。 为此刻的迭代次数N′>N N′
3 拉格朗日蝙蝠算法
3.1 求解GAP的拉格朗日松弛算法
拉格朗日松弛算法(Lagrangian relaxation,LR)是一种分解协调算法,由Herd和Karp于1970年提出,最早用于解决旅行商问题。随后被用于各大领域,现已成为解决组合优化问题时产生解的下界的一种不可或缺的方法。拉格朗日松弛算法的基本原理是通过引入拉格朗日乘子λj,将原问题中的某些约束作为惩罚项吸收到目标函数中,使原问题成为较易解决的拉格朗日松弛问题。通过拉格朗日乘子松弛约束式(3),松弛后的GAP可表示为

s.t. 式(2)和式(4)
再通过标准次梯度优化算法修正拉格朗日乘子,求得拉格朗日对偶问题(Lagrangian dual,LD)的解。其中,拉格朗日对偶问题表示为

s.t. 式(2)和式(4)
利用标准次梯度优化算法,第t时刻对拉格朗日乘子的修正为

式(11)和(12)为拉格朗日乘子步长的更新;
式(13)表示拉格朗日乘子的更新。
通过以上方式求解拉格朗日对偶问题,解的目标函数值为原问题最优解的下界。但由于约束条件被松弛,扩大了GAP问题可行解的范围,导致松弛后的解不一定是原问题的可行解。
为了保证解的可行性,本文对拉格朗日对偶问题的解进行可行化,具体方式为:搜索没有被分配的工作,选择完成该工作消耗量最小的代理器为其服务。同理,搜索有多个代理器服务的工作,选择完成该工作时消耗的资源量最小的为其服务,执行此操作直至所有工作都只有一个代理器为其服务。检验每个代理器消耗的总资源量,若超出自身占有,按照d的调整方式进行修正。可行化后的解为原问题的可行解,对应的目标函数值为原问题最优解的上界。
3.2 求解GAP问题的拉格朗日蝙蝠混合算法设计
将离散蝙蝠算法和拉格朗日松弛算法相结合,提出全新的解决GAP问题的拉格朗日蝙蝠算法(Lagrangian bat algorithm,LR-DBA)。两种算法取长补短,离散蝙蝠算法求得GAP问题最优解的上界,此解为标准次梯度提供优秀上界;拉格朗日松弛算法求得GAP问题最优解的下界,当可行化后的解优于蝙蝠算法的最差解时,替代最差解;求得的上界、下界相互逼近,逐渐接近GAP问题的最优解。该算法的具体步骤如下:
步骤 1 初始化蝙蝠种群。蝙蝠种群个数s,初始音量Ai0,初始脉冲发生率ri0,最大迭代次数N,初始化蝙蝠个体位置xi。
步骤 2 蝙蝠速度和位置更新。计算得出最优蝙蝠x*。通过式(5)更新速度,利用单点遗传基因换位算子更新位置xnew。
步骤 3 局部搜索。若rand>ri,从最优解集中选一个解,利用单点遗传基因换位算子产生一个局部解xnew。
步骤 4 若rand<Ai且,则更新当前满意解及其对应的目标函数值,并通过式(6)增大 ri,式(7)减小 Ai。
步骤 5 排列蝙蝠并找到当前最优x*,计算GAP问题最优解的上界,记为UB。
步骤 6 运用标准次梯度算法求解拉格朗日对偶问题,求得的解为GAP问题最优解的下界,记为LB。
步骤 7 对拉格朗日对偶问题的解进行可行化,求得GAP问题最优解的上界,记为 U B′。若可行化后的解优于蝙蝠算法的最差解,则更新蝙蝠算法最差解。
步骤 8 N′=N′+1,若 N′<N,则转步骤2;否则,结束搜索并输出结果。
4 仿真实验与分析
为了验证算法的有效性,测试了Beasely的OR-library中的16组标准测试算例。其中,包括12组小规模算例,每组小规模算例中包含5个小算例;4组较大规模算例,每组较大规模算例中包含 3个小算例。在 Intel(R) Core(TM)i5-3320 CPU@2.60 GHz 2.60 GHz内存,64 位Windows 8操作系统的环境下利用Matlab R2015a进行编程实现和数据处理。该混合算法的初始参数设置为:蝙蝠种群数量s=20,迭代次数N=500,初始音量ri0=0.25,初始脉冲发生率 ri0=0.5, α =β=0.9, π =2,拉格朗日乘子λj的初始值参照文献[20]的取值方式,即 λj=max cij,j∈ J。
为了测试LR-DBA混合算法的求解性能,将其与DBA算法进行比较。表1和表2分别列出了小规模和较大规模算例的相关数据。表中,运行时间为500次迭代的总时间;算例的目标函数值为随机运行5次,取最好一次为满意解;G为本文求得的满意解和文献[21]的最优目标函数值之间的差值;平均运行时间和平均G为一组算例中5个小算例的平均值;达到最优算例个数为一组算例中5个小算例中达到最优解的个数。C为目标函数值,D为最优目标函数值。G的计算式为
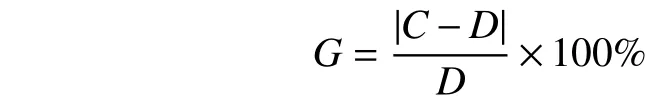
由表1可以看出,DBA算法求解的60个算例中只有2个达到最优解,而用LR-DBA混合算法求解时有10个达到最优,且12组算例的G均小于1%,几乎达到最优解,表明LR-DBA混合算法在求解小规模算例中结果较好。表2中,对比DBA算法和LR-DBA混合算法的G,很明显看出LR-DBA混合算法在求解较大规模GAP算例中也有很大的优势,LR-DBA混合算法求解的12个算例中除gapc3以外,其他算例的G均在5%以内,而DBA算法求解所得G最大达到15%,且12个算例中有7个G都大于5%。分析全部算例,可以看出,LR-DBA混合算法在求解GAP问题算例时具有更好的全局搜索能力,且收敛精度较好。
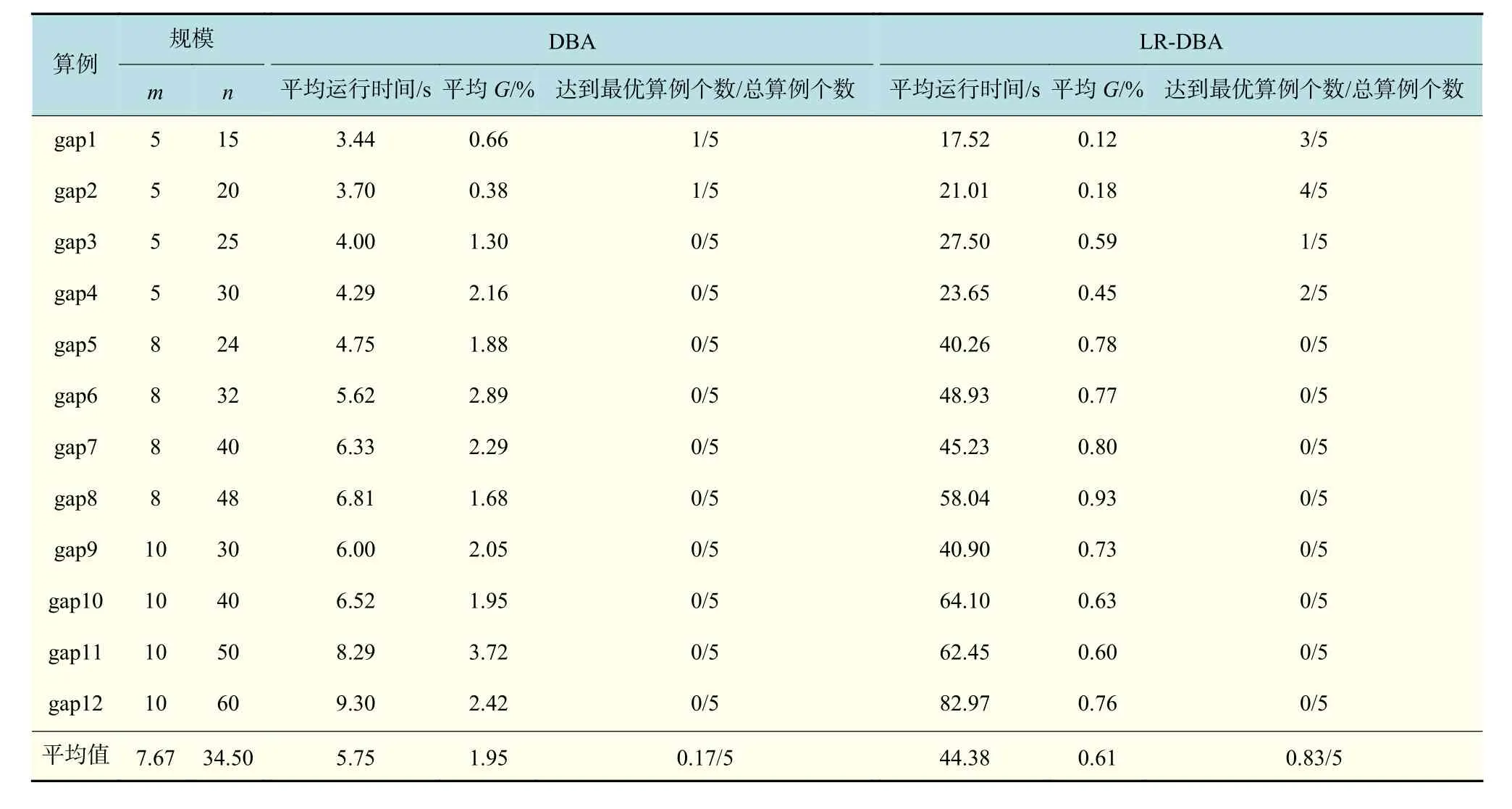
表1 小规模GAP算例计算结果Tab.1 Calculating results of a small-scale GAP
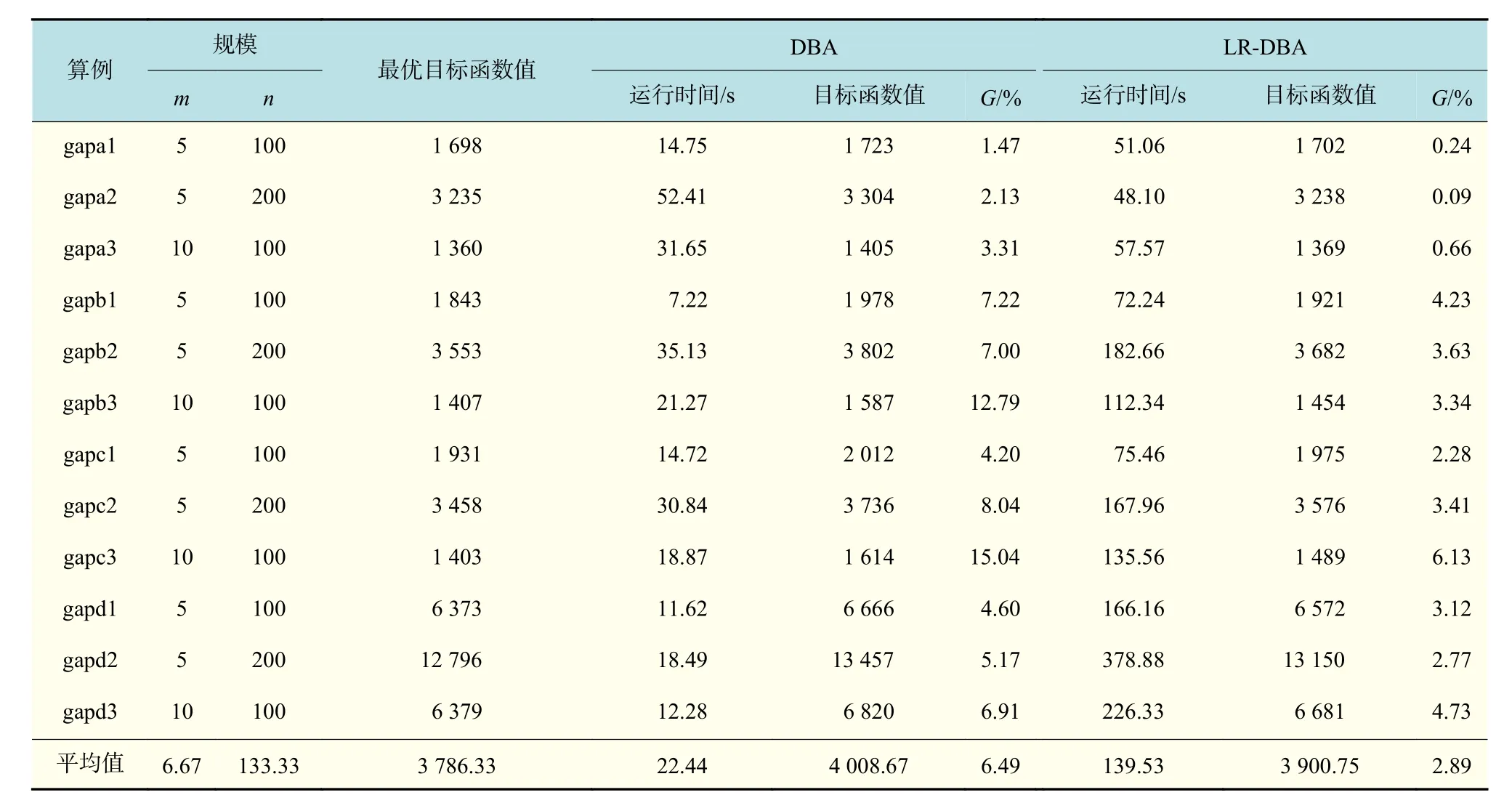
表2 较大规模GAP算例计算结果Tab.2 Calculating results of a large-scale GAP
综合分析表1和表2的实验数据,LR-DBA混合算法求解GAP问题性能优异,尤其针对小规模算例。但由于LR-DBA混合算法结合了拉格朗日松弛算法,在求解小规模GAP问题时,LR-DBA混合算法的平均运行时间几乎是DBA算法运行时间的8倍,在较大规模的求解中,LR-DBA的平均运行时间也是DBA算法的6倍,说明混合算法的收敛速度慢。
为了更直观地展现LR-DBA混合算法的求解效果,本文以gapa3为例,给出求解GAP问题的迭代过程图,如图2所示。

图2 算例gapa3的迭代过程图Fig.2 Iterative process of the numerical example gapa3
由图2可以看出,混合算法在求解过程中迭代的前期收敛速度快,能在较小的迭代次数得到一个较好解,但后期收敛速度较慢。综合比较迭代次数、目标函数值和运行时间,可以看出,拉格朗日松弛算法一方面扩展了蝙蝠算法的搜索范围,但另一方面也使得混合算法的运行时间变长。
5 结束语
应用BA算法来解决基本GAP问题,并针对GAP问题的特点,在基本BA算法框架基础上引入遗传算法单基因换位算子,提出DBA算法;在此基础上,将DBA算法与LR算法结合组成LR-DBA混合算法,具有较强的全局搜索能力和鲁棒性。通过大量的仿真实验结果,表明LR-DBA混合算法求解GAP问题的性能优于DBA算法。
本文不仅为广义分配问题提供了一种优异的求解方法,同时也拓宽了蝙蝠算法在离散问题上的进一步应用。但是,较现有的求解GAP问题的其他智能优化算法(如禁忌搜索和蚁群混合算法[11]、混合遗传算法[22]、禁忌搜索算法[23]),LR-DBA混合算法的性能较差,并且如仿真实验部分所示,LR-DBA混合算法在求解效率上也有待提高,这将是本文今后进一步研究的内容。
