基于MATLAB的分段型模拟信息转换器仿真研究
2019-06-06王晓波蒋铁珍
王晓波,蒋铁珍
(安徽大学,安徽 合肥 230601)
0 引 言
MIMO雷达在对空中机动目标的探测、识别、跟踪和目标参数估计有着良好的性能和优势[1],尤其是分布式孔径相参合成雷达,对收发信号进行全相参合成而获得大的功率孔径积,可对空中的隐身目标实现远距离搜索和高精度跟踪,但此时收发相参的大孔径合成是信号级合成,会引起系统数据传输量大幅度增加,传输到中心站的数据率也显著提高,使后续计算机处理数据的采样率和运算量急剧增大[2-3]。传统Nyquist采样理论是以不低于信号带宽的两倍频对信号进行采样,对得到的采样点经傅里叶变换来精确重构原始信号。而面对信号的高采样率、海量处理及存储时,信号处理系统需承受的压力急剧增大[4],因此,以传统采样理论为指导的ADC在MIMO雷达信号处理系统中越来越凸显出很多方面的不足,如效率低下、硬件结构复杂、数据资源浪费、成本昂贵等。
CS理论表明:如果信号本身是稀疏的或在某个稀疏基下是稀疏的,则可以寻找或者构造一个与稀疏基不相关的测量矩阵,对原始信号进行不相关测量,得到的观测值包含原始信号的全部有用信息,通过求解优化问题从少量的观测值中实现近似或精确重构原始信号[5]。在CS理论指导下的AIC系统,可远低于Nyquist采样频率对信号采样,经算法优化进而重构原始信号,相对于在信号处理很多方面受限的ADC突出了优势。现有很多学者对AIC系统进行了研究,比如张弓、文方青等人综述了AIC的基本理论基础,描述了国内外AIC系统的研究进展,并展望了未来的研究发展方向[6]。陈宇科、汪立新等人对预调制型和直接型AIC系统仿真分析,并得出以远低于奈奎斯特采样率采样的AIC系统能够精确重构原始信号的结论[7]。刘渊、杨泽林等人以MATLAB/Simulink 为平台,建立了一种AIC数据处理系统模型,仿真结果得出了AIC系统建模的可行性[8]。赵磊、俞阿龙等人在无线传感网络中基于CS理论,以MATLAB为平台构建了AIC模型并仿真,得到用较少的观测值可精确重构原稀疏信号的结论[9]。陈科帆、孙彪等人结合CS理论改进了传统随机解调结构的AIC系统,并设计其系统结构和软硬件实现方法,很大程度上减少传感网络能耗和硬件成本[10]。将以CS理论为指导的AIC系统应用在MIMO雷达的接收机中,不仅可以减少雷达系统面对高数据率的压力,还可以降低系统能耗和硬件成本,但AIC系统中不同的支路数也会对原始信号的恢复精度和系统结构复杂度产生很大影响[11]。目前在对AIC系统建模仿真中,对支路结构简单、重构精度底的预调制型AIC和支路结构复杂、重构精度高的直接型AIC研究较多,没有在MATLAB/ Simulink中对精度上优于预调制型AIC、支路结构上简于直接型AIC的分段型AIC进行系统建模和仿真。因此,为更好平衡AIC系统在海量信号处理中的采样率、数据精度、结构复杂度和硬件成本,本文结合CS理论,在MATLAB/Simulink中建立了一种分段型AIC 系统模型,实现对稀疏信号的低速率采样和高精度重构,体现出分段型AIC系统的高精度、简结构、低成本的性能。
1 压缩感知理论
CS理论应用研究的关键内容包含稀疏信号、测量矩阵和重构算法。若长度为N的一维离散信号xRN,在某个稀疏基Ψ下是稀疏的,则x可以用Ψ线性表示为:

(1)
其中α=[α1,α2,…,αN]T,Ψ=[Ψ1,Ψ2,…,ΨN], ||α||=K(K≪N),说明x在稀疏基Ψ下有K个非零元素,即K稀疏,矢量α是原信号x在稀疏基Ψ下的稀疏表达。典型的稀疏基有傅里叶稀疏基、小波稀疏基以及过完备字典等。
根据CS理论,在对原始信号测量过程中,用一个M×N(M≥K)维与稀疏基不相关的测量矩阵Φ对x进行线性投影,得到线性的观测值矩阵y:
y=Φ·x=Φ·Ψ·α=Θ·α
(2)
其中,Θ叫做恢复矩阵,且是M×N维的。(2)式是一个方程个数小于未知数个数的欠定方程组,所以为了确定从观测值矩阵y中准确的重构原始信号,测量矩阵Φ需要满足和稀疏基Ψ之间具有不相干性以及有限等距约束(Restrieted Isometry Property,RIP) 性质,即对于常数δK(0,1)及任意K稀疏信号x,由测量矩阵Φ和稀疏基Ψ构成的恢复矩阵Θ满足[12]:
(3)
在实际应用中,观测数M需要满足M≥c·K·In(N/K),其中c为一个很小的常数,从而在很大程度上同时满足测量矩阵与稀疏基的不相干性和RIP性质。典型的测量矩阵有傅里叶随机矩阵、服从伯努利分布的1矩阵、高斯随机矩阵、哈达玛矩阵等。
而利用测量矩阵观测到的离散观测值,须经重构算法计算处理,才能完成对原稀疏信号的重构。目前有很多重构算法可实现对稀疏信号重构,如基追踪算法、匹配追踪算法、正交匹配追踪算法以及分段正交匹配追踪算法等。
2 分段型模拟信息转换器结构原理
CS理论是在离散信号的背景下提出,为了从连续信号中直接得到离散的观测值,Saini Kirolos等人提出一种模拟信息转换器,即将CS理论应用于处理模拟信号的方法[13]。该方法避免了模拟信号数字化过程,可突破Nyquist采样的限制直接采样模拟信号得到离散的观测值,AIC系统处理模拟信号的过程如图1所示。

图1 AIC系统处理模拟信号的过程
AIC主要有三种类型的实现结构:预调制型AIC结构,直接型AIC结构和分段型AIC结构[14]。预调制型AIC结构原理框图如图2所示,该结构处理模拟信号的主要过程包含信号的伪随机调制、滤波器滤波、低速均匀采样。
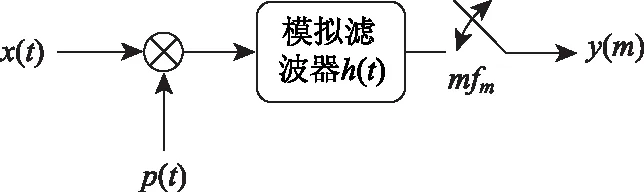
图2 预调制型AIC结构原理框图
直接型AIC结构的原理框图如图3所示,该结构在处理信号时,主要是将模拟信号与不同支路的不同伪随机序列混频后进行积分运算,然后被低速均匀采样,得到离散观测值。
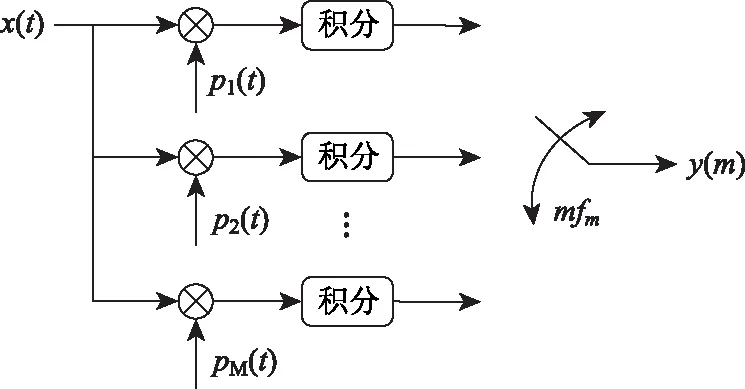
图3 直接型AIC结构原理框图
由图3可知,不同的伪随机序列、多条积分支路、每条支路得到一个观测值是直接型AIC结构的特点。因此,随着模拟信号的稀疏度K增大,依据M≥c·K·In(N/K),其观测数M就会增多,直接型AIC的积分支路条数会增加。当稀疏性K很大时,急剧增加积分支路的直接型AIC相对于图2的预调制型AIC,积分支路条数会多很多,但由于观测值之间的不相关性,通过直接型AIC重构信号精度会比预调制型AIC高。
对于直接型AIC,支路数会随着观测值的增加而增加,而且结构的实现也会变得越来越复杂,所以为了避免AIC结构过于复杂,分段型AIC就以很小的重构精度为代价,缩少积分支路的数量,可以让K值较大的稀疏信号在采样处理中相比直接型AIC变得简单。分段型AIC的原理框图如图4所示。
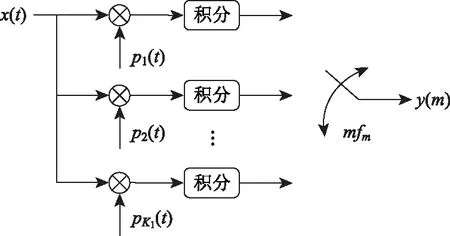
图4 分段型AIC结构原理框图
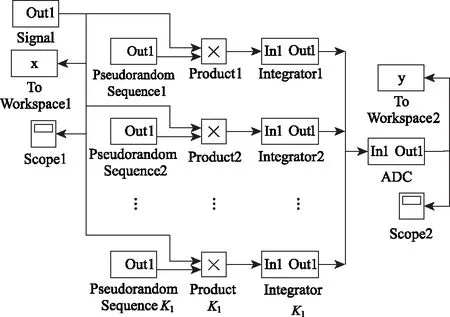
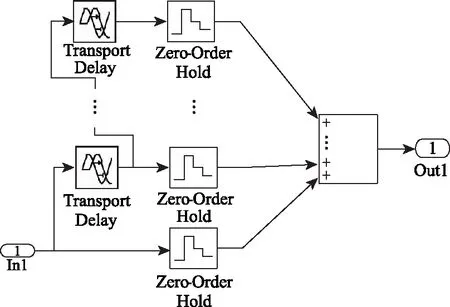
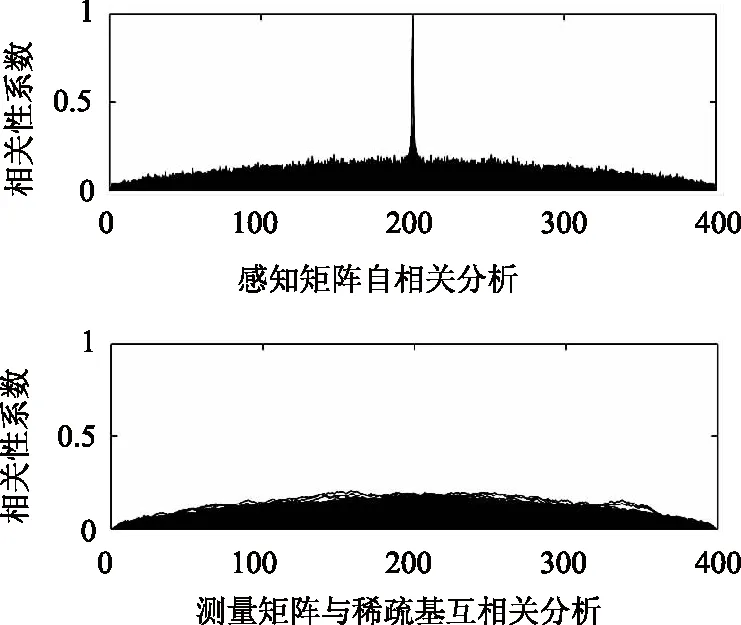
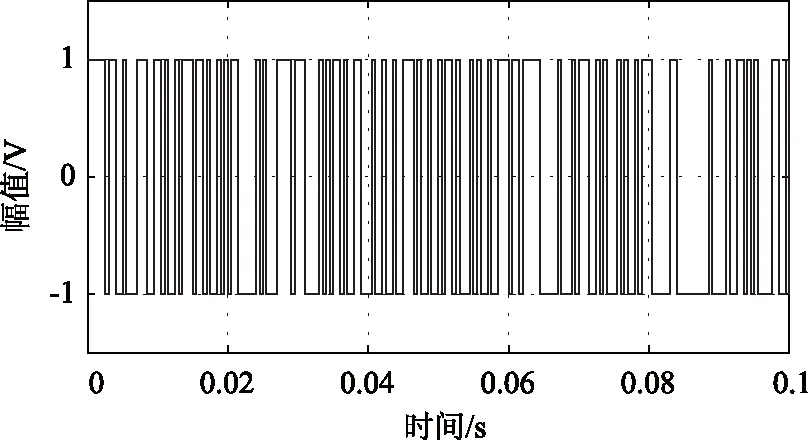
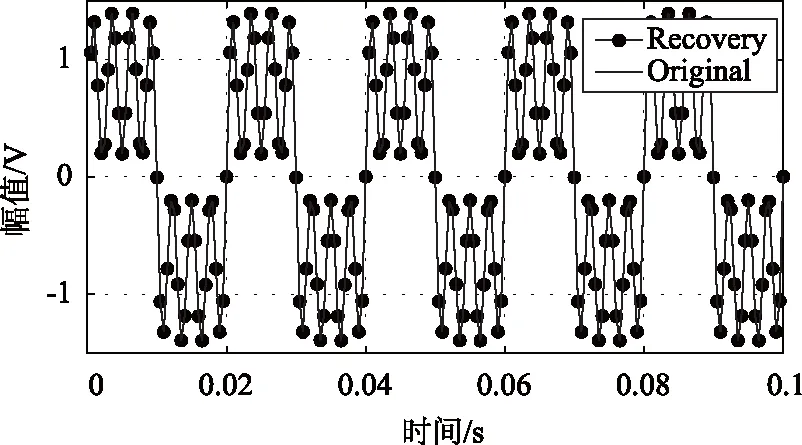
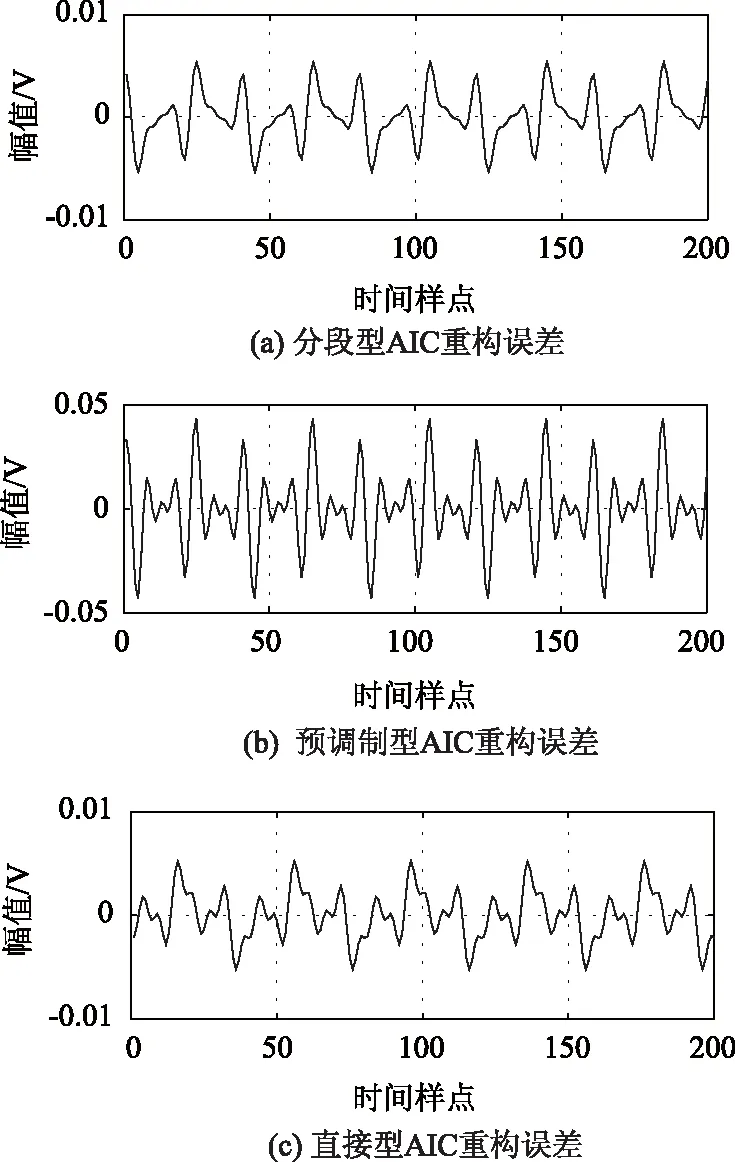
比较图3、图4可得,分段型AIC的积分支路明显与直接型AIC不同,两者其它的结构基本一致。分段型AIC的积分支路K1 第一步:将原积分周期分成H个积分段,第k条积分支路对混频信号进行H次的积分采样可得到H个采样点,即yk=[yk,1,yk,2, …,yk,h],k=1, 2, …,K1,h=1, 2, …,H,那么全部支路的采样点可以组成一个K1×H的矩阵,其测量点yk为第k条积分支路的完全测量点,表达式为: (4) 第二步:在得到的这些采样点构成的K1×H矩阵中,取第一对角线上的H个采样点的集合作为yK1+1,第二对角线上的H个采样点的集合作为yK1+2,以此类推,得到K2×H的拓展采样点矩阵,其拓展测量点yK1+k为第K1+k个完全测量点,表达式为: (5) 其中k=1,2,…,K2,K2≤K1。如下图5是拓展采样点的扩展方式; 图5 拓展采样点的扩展方式 第三步:类似于拓展采样点的扩展方式,原为K1×N的测量矩阵Φo经扩展后可变为(K1+K2)×N矩阵的测量矩阵Φoe,其中K1>H。把原测量矩阵Φo第k行记为φk=[φk,1,k,2,…,k,H],为降低复杂度,使得N/H的结果为整数。扩展后的测量矩阵Φoe的矩阵表示为: (6) 根据图4的分段型AIC结构,在MATLAB/Simulink环境下设计分段型AIC模型。其结构包含了信号源模块(Signal)、伪随机序列模块(Pseudorandom Sequence)、乘法器(Product)、积分模块(Integrator)和ADC模块。分段型AIC的模型设计总体结构图如图6所示。 图6 分段型AIC模型设计总体结构图 信号源模块是输入分段型AIC系统的稀疏信号。伪随机序列模块是用于产生伪随机序列。它是由伯努利二进制发生器产生等概率的0、1伪随机序列,通过2倍增益再与-1相加,就能够产生等概率的-1、1伪随机序列。伪随机模型的设计如图7所示。 图7 伪随机序列模块结构图 积分模块是通过对每多个采样点的累加从而降低模拟转换器的采样速率。其模块结构是由多个延时模块(Transport Delay)、采样保持模块(Zero-Order Hold)和累加模块实现。如果输入信号的采样速率为f1,在应用了CS理论以后其AIC的采样速率降到f2(f2≪f1),使得低速ADC的每个采样值是由输入信号连续的f1/f2(通常为整数)个分量累加而来的。积分器中延时支路个数的选取是根据信号总长度N除以压缩比f1/f2减1得来的。积分器模型的设计如图8所示。 图8 积分器模块结构图 ADC模块是将低速采样得到的测量值数字化。先用限幅器(Saturation)将信号限幅在(-1,1)内,目的是为了减小后面量化误差。其中中继模块(Relay)以0为分界,大于0输出为正极性,小于0输出为负极性,采样值经取模模块(Abs)取模后,用间距为1的量化模块(Quantizer)进行量化,最后通过位数设置为7的二进制转换模块(Integer to Bit Converter),该模块可将0~127的十进制数转换为7位二进制数,其输出作为量化后的低7位。ADC模型的设计如图9所示。 图9 ADC模块结构图 根据上面所介绍分段型模拟信息转换器结构框图,在MATLAB/Simulink中搭建分段型AIC结构模型。将测试信号经该系统并结合MATLAB编程进行仿真,对AIC系统所测量到的观测值进行拓展变换,与原观测值共同组成观测值矩阵,将经拓展后的M个观测值和测量矩阵Φoe,利用OMP算法对测试信号重构。该测试信号重构信号的过程如图10所示。 图10 分段型AIC系统对测试信号重构过程 测试信号采用多谐波正弦信号,时域信号为:x(t)=sin(2πft)+0.3sin(6πft)+0.2sin(10πft) +0.7sin(14πft),基波频率为f=50Hz。该测试信号为稀疏度K=8的稀疏信号,根据压缩感知理论,观测数M、稀疏度K以及信号维数N应该符合M.c.KIn(N/K),所以设测试信号维数N=200时,需满足M26,令积分支路K1=20,拓展积分支路K2=K1=20,则总观测数M=K1+K2=40。信号的Nyquist采样频率为fs=2 000 Hz,AIC的采样频率为fm=400 Hz,则信号压缩比为fs/fm=5∶1,积分器中延时支路取39个。 分段型AIC中每条支路上与原始信号相乘的伪随机序列都不相同,为的是每个观测样点之间是不相干的,经图5的拓展方式拓展采样点,也是为了减小采样点矩阵每行之间的相干性。通过对拓展后的测量矩阵与稀疏基的RIP性质和相干性分析,其测量矩阵与稀疏基均符合RIP性质,且从图11可以看出感知矩阵的自相关性系数和测量矩阵与稀疏基的互相关性系数都很小。 图11 分段型AIC的相关性分析 在仿真过程中,所得的图12~图15分别是:稀疏度K=8的测试信号、其中一条支路(P1)的伪随机序列信号、其中一条支路(P1)所观测到的AIC信息矢量以及用OMP算法重构的信号与原始信号波形图对比。如图15所示,可以看出重构信号和测试信号基本能够全部对应,所以通过该AIC系统模型可以较好的恢复原稀疏测试信号。 图12 稀疏度K=8的测试信号 图13 其中一条支路(P1)的伪随机序列信号 图14 其中一条支路(P1)所观测到的AIC信息矢量 图15 重构信号与测试信号的对比 将原稀疏测试信号混入一部分加性高斯白噪声,分析该分段型AIC系统对测试信号的重构能力。令K=8,K1=K2=20,即M=40,将混入加性高斯白噪声的测试信号用该分段型AIC系统模型进行仿真重构。仿真结果见表1。 表1 对该AIC系统加入噪声信号的重构分析 从表1中可以看出,随着信号中加入高斯白噪声信噪比的增强,信号的恢复信噪比也在逐步加大,重构误差逐步变小,当信噪比大于70dB时,信号的恢复信噪比和重构误差将维持稳定不变。 同时为了进一步分析该分段型AIC系统模型,在稀疏度K=8、积分支路K1=20的情况下,以不同的拓展积分支路K2,获得不同的观测数M,将测试信号在理想情况下用该分段型AIC系统模型进行重构。仿真结果如图16所示。 图16 K=8时不同观测数下的恢复信噪比 由图16中可以看出,当K2<5,即M<25时,此时信号的恢复信噪比均小于20 dB,因此不能够精确重构原测试信号;但当K2>5,即M>25时,此时信号的恢复信噪比均大于40dB,因此能够较好的重构原测试信号。 紧接着在K=8,K1=K2=20,即M=40的情况下,由MATLAB/Simulink仿真出该分段型AIC系统对原稀疏测试信号在理想情况下的重构误差与同条件下的预调制型AIC系统、直接型AIC系统的仿真结果进行比较,如图17所示。 图17 三种AIC结构对原稀疏信号重构的误差比较 从图17中可看出,直接型AIC对信号的重构性能最优,分段型AIC次之,预调制型AIC最差,这与我们在前面理论分析所得的结果相同。 根据以上仿真实验结果分析可以得到: (1)该分段型AIC系统模型符合CS理论中要求观测数M≥c·K·In(N/K),且满足实验条件时可以精确的重构原始信号。 (2)从表1中可观察到,该分段型AIC系统在对信噪比在30 dB以上的信号可以较好的重构,且大于70 dB时重构信号性能保持不变;在较小的信噪比的时候,比如10 dB时重构原始信号的误差将变的很大,即不能重构原始信号。因此该分段型AIC系统在对含小信噪比噪声的原始信号重构能力上有待提高。 (3)该分段型AIC系统在K=8,K1=20时,在不拓展积分支路的情况下,即K2=0,从图16中可以看出,此时不能重构原始信号,但随着K2的增加,当满足了M≥c·K·In(N/K)时,可重构原始信号,且当K1=K2=20时,从图18中看出重构误差接近M=40的直接型AIC系统。而实际上分段型AIC的积分支路比直接型AIC系统少了一半,因此在重构误差相近的情况下,分段型AIC系统在成本资源节省和硬件结构实现上相比较直接型AIC系统具有很大的优势。 本文基于CS理论研究了分段型AIC的结构和基本原理,利用MATLAB/Simulink对分段型AIC系统进行了建模和仿真分析。分析实验的仿真结果得出该分段型AIC模型可以实现对原始稀疏信号的精确重构,重构误差仅为0.0027。所以,在面对MIMO雷达系统对空中机动目标识别和多目标跟踪中产生的高数据率和高采样率时,该分段型AIC系统不仅可以很好的替代传统ADC系统,有效解决传统采样理论所遇到的采样效率压力、数据资源压力、结构成本压力等挑战,而且为以后将该分段型AIC系统应用到MIMO雷达系统中以获得最佳匹配度以及更多适用场景提供了指导。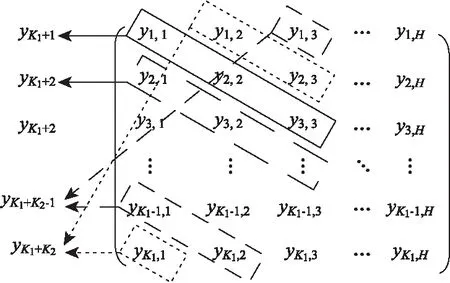
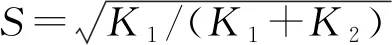
3 分段型AIC模型建立与仿真分析
3.1 分段型AIC的模型建立


3.2 分段型AIC的仿真结果及分析





4 结 语
