考虑随机冲击的单部件退化系统维修策略优化研究∗

吴 倩 陈 童 尹东亮

（1.海军工程大学海军舰船振动与噪声研究所 武汉 430033）（2.船舶振动噪声重点实验室 武汉 430033）（3.海军工程大学管理工程与装备经济系 武汉 430033）

1 引言

大型复杂装备或高新技术设备结构精密、维修难度大，针对其制定合理、高效的维修策略往往能增加装备使用时限，提高系统可靠性。在该类装备实际使用过程中，一般通过故障检测判断系统状态，选择合适的维修方式［1］。预防性维修可提前排除故障隐患，但其维修不完全，并不能使装备系统“修复如新”；换件维修［3］在装备失效后更换备件，更换后装备系统“修复如新”。这两类维修方式可贯穿装备使用全过程，相互补充促进，是较为常用的两种维修保障方式［2～3］。因此，结合该类装备使用与维修特点，合理控制检测节点，判断系统是否需要维修，从而选择合适的维修方式并确定下次检测节点以制定维修策略是科学、合理的。该决策过程循环反复，同时系统性能具有随机性，可看作是一个与时间相关的随机序贯决策问题［4］，半马尔科夫决策过程（Semi-MDP）［5］被广泛应用于该领域。

Zhang等［6］通过结合各类维修行为提出了一个基于点的值迭代算法，有效提高了Semi-MDP在状态转移不确定和观测不确定情况下机器维修中的适用性；Jiang等［7］将城市列车车轮受到直径或法兰厚度超限的状态监测和定期检查过程模拟为Semi-MDP，考虑不完全车轮保养，最大限度地减少每单位时间维护成本；Srinivasan等［8］考虑系统当前状况以及劣化速度的不确定性，采用了部分可观察的半马尔可夫决策过程（POSMDP）对维修决策进行了优化。

在对这类复杂装备进行维修策略优化建模时，由于其集成度高、组成部件相关性强，往往将其整体看做单部件系统，以便于解析建模，同时较为符合实际情况，如舰船动力系统、核电系统等。而装备系统失效过程一般由系统内部劣化机理和外部环境因素共同作用产生。系统内部性能和工作效率一般随着时间推移不断退化，直至失效，如机械磨损、橡胶老化等；同时外部环境因素影响使系统受到冲击也会造成系统劣化，影响装备内部性能，如机械设备腐蚀，电子元件电压不稳等，这两者共同作用，使系统表现出多状态特性。因此，考虑外部冲击的退化系统于20世纪70年代被提出［9］，广泛应用于系统维修策略研究中。

Zhou等［10］考虑不完全预防性维修，假设维修后系统失效率服从指数分布，冲击与退化过程为泊松分布，分析了以维修费用最低为目标的维修策略；张延静等［11］针对同时受自然退化和随机冲击影响的单部件系统，假设冲击过程为泊松过程，冲击量服从正态分布，提出了基于状态的维修策略，建立了一个成本率函数；Huang等［12］利用指数分布建立了包含连续平滑的退化和冲击过程的设备维修模型，获得了最优的劣化阈值和平均费用率。

上述研究为了求解方便，一般假设部件寿命、维修时间等服从指数分布、正态分布等各类典型分布，这在一定程度上导致模型解析难度大，适用范围窄。为了解决这一问题，Neuts［13］在 1975 年首次将Phase-type（PH）分布作为指数分布的一般化形式提出。PH分布族在经历过大量运算后依然具有封闭性，同时能近似拟合非负半轴上的任何概率分布，可将各类典型分布统一表示为PH形式，降低了解析计算难度，又具有一般性，使得其被广泛应用于各类随机模型。

Ruiz-Castro等［14］研究了考虑外部冲击与内部退化的多状态设备系统，利用PH分布对随机检测间隔时间进行描述，对预防性维修阈值、时机进行了优化；Montoro-Cazorla等［15］假设系统冲击来源由马尔可夫过程决定，预防性维修时间服从PH分布，系统失效后换件，得出了故障发生率等参数；Yu等［16］考虑系统受冲击过程为PH更新过程，经历一定次数维修后更换备件，备件采购时间服从PH分布，建立了系统更换优化模型。

综上，本文以考虑随机冲击的单部件退化系统为研究对象，系统所有性能参数等只能通过检测获得，系统接受随机检测，单一维修台可进行不完全预防性维修和换件维修两种维修活动，将系统性能划分为多个离散状态，建立了基于PH分布的系统维修策略优化模型，解决了随机检测与两类维修活动综合优化的问题，利用值迭代算法，确定了系统最佳的预防性维修控制阈和各状态对应的检测间隔时间，以达到长期运行条件下的平均费用率最低且系统稳态可用度满足要求。最后，通过算例验证了模型的正确性与适用性，演示了费用参数变化对最佳策略的影响。

2 PH分布相关基础知识

定义1［17］:若一个非负随机变量X服从连续PH分布，那么它的分布函数为

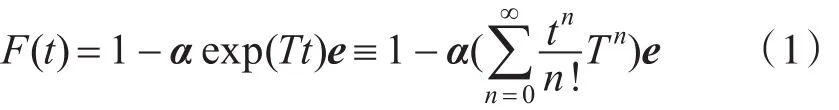
其中:

1）t≥0，e是全部元素都为1的列向量；

2）α是次随机矩阵，含m个非负元素的行向量，m为正整数，αe≤1；

3）T是m阶矩阵，该矩阵对角线元素全为负，其他元素非负，矩阵可逆，且每行元素之和是非正的。

定义2［17］:连续时间马尔科夫链{I(t),t≥0}，其状态空间由m+1个状态{1，2，3，…，m，m+1}组成，无穷小生成元表示为

其中，T为PH分布的生成元。由于每一行元素之和均为0，则可得T0=-Te。状态m+1的转移概率为0，则状态m+1为吸收态。

定义3［18］:一个m×n阶矩阵A和一个p×q阶矩阵B的Kronecker积被定义为

根据式（3），可得出Kronecker积有如下性质:

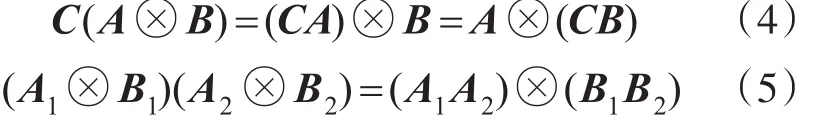
定义4［18］:一个m阶矩阵 A和一个n阶矩阵 B的Kronecker和被定义为

其中，In和Im分别表示m和n阶的单位矩阵。

3 问题描述与假设

假设某单部件系统随运行时间的推移性能不断退化，同时运行过程中会受到外部随机冲击的影响，冲击会对系统造成一定的损伤，加快系统退化。系统内包含单一维修台，维修台始终处于完好状态，可进行预防性维修工作，系统失效后立即更换。

下面对问题做进一步假设:

1）在系统运行过程中，系统所有性能参数、冲击次数、冲击损伤量只能通过检测获得，为了建模方便，将系统划分为n个状态，每个状态i所对应的系统性能参数范围不同，根据检测结果确定系统所处状态i。检测时间tin也服从连续PH分布，有f阶PH表示(δ,R)。检测时系统停机，不会继续劣化。

2）将系统n个状态划分为四部分，i=1为全新状态；当2≤i≤m时，不需要进行预防性维修，为完好状态集；当m+1≤i≤n时，需要进行预防性维修，为劣化状态集；当i=n+1时，系统维修费用及难度较高，为失效状态，直接更换，系统各状态停留时间服从PH分布，有hi阶PH表示(αi,Ti)。

令Pij=[Pij]n×n表示系统受到退化影响由状态i转移到状态 j的状态转移概率矩阵，其中1≤i,j≤n 。 根 据 PH 分 布 的 定 义 ，P0=(P1(n+1)P2(n+1)P3(n+1))T为系统受到退化影响转移到失效状态的概率矩阵，即转移到状态i=n+1的概率。

3）外部随机冲击对系统造成一定的损伤量，根据系统状态划分，将损伤量大小转化为系统状态劣化程度，即在某次检测时，发现系统在两次相邻检测之间受到一定次数的随机冲击，这些冲击所造成的损伤量可使系统由状态i瞬间退化到状态i*，i＜i*。令随机冲击到达为PH更新过程，有ρ阶PH表示 (λ,W)。

令Dij=[Dij]n×n表示系统在两次相邻检测之间受到退化和外部冲击共同作用由状态i转移到状态 j 的 概 率 矩 阵 ，其 中 1≤i,j≤n 。D0=(D1(n+1)D2(n+1)D3(n+1))T表示系统在状态受到冲击与退化双重影响突发失效的概率，即转移到状态i=n+1的概率。

4）预防性维修时间tma服从PH分布，有l阶的PH表示(θ,S)，系统更换时间tre服从PH分布，有v阶PH表示(γ,B)。考虑不完全预防性维修，系统修复后不会修复如新，而是处于完好状态，即i≠1，在状态i对系统进行维修后系统处于状态 j的概率矩阵为 O32=[Oij](n-m)×(m-1)，其中 m+1≤i≤n ，2≤j≤m。

5）系统预防性维修时间、检测时间、更换时间以及各状态停留时间相互独立。

在t=0时刻，系统以完好状态开始运行，期间会经历退化、随机冲击、检测、不完全预防性维修、直至失效更换，如图1所示。

图1 系统运行时间轴

6）系统检测费用、预防性维修费用、因检测或失效造成的停机损失、系统更换费用分别为cin、cmi（1≤i≤n）、ci（1≤i≤n+1）、cr，其中，cmi（1≤i≤n）表示不同状态i的维修费用不同，同时因系统失效造成的停机损失cn+1应比因检测造成的停机损失大，故 cn+1＞ci，1≤i≤n。

7）检测采取随机检测，检测方式决定了维修决策过程中的状态转移情况，检测间隔时间与当前状态有关，需要根据当前状态确定下一次决策点，即检测间隔时间，令其服从一般分布，概率分布函数为Γ(t)，表示该次检测距前一次系统维修决策后开始运行的时间间隔。由于PH分布具有较强的适用性，可以在非负半轴上近似拟合任意分布，故可假设检测间隔时间服从PH分布，有g阶PH表示 (ζ,U)。

8）根据系统运行状态转移图可以看出，从系统开始运行到系统失效更换完成构成一个寿命周期T。若经过时间t系统运行所需费用为C(t)，那么由更新过程相关理论可得系统长期运行平均费用率ψ可以看作是部件寿命周期内的平均费用率，即

其中，E(C(T))、E(T)是由检测间隔时间和维修控制阈（即临界状态m+1）决定的。

9）若经过时间t系统正常工作时间为t*，可得系统长期运行稳态可用度As:

10）目标函数:通过优化检测间隔时间和确定维修控制阈使得平均费用率最低，稳态可用度As大于。

4 Semi-MDP参数设置

根据半马尔可夫决策过程的定义，划分六元组{S,A(i),pij(a),T(·|i,j,a),r(u,i,a,j,t),V|i,j∈ S,a∈A(i)}，根据问题假设具体参数含义如下:

1）系统状态空间S:考虑外部冲击与内部退化的相关性，将系统状态空间划分为S={1,2,…,n+1}；

2）决策行动集:A(i)={a,Γ(t,φi)}。其中，φi表示根据在该次随机检测点所确定的系统所处状态i决定决策行动从而确定检测间隔时间，再由此作为参数得出检测间隔时间所服从分布的具体数

3）系统状态转移矩阵:根据PH分布的定义将系统状态转移矩阵Pij转化为系统劣化的Q矩阵，其中系统状态转移主要由以下情况造成:退化和冲击、预防性维修、替换；

4）转移时间Δt:考虑检测时间、维修时间和替换时间，则两次决策时间间隔可表示为:（1）检测系统状态i≤m，不进行预防性维修，系统检测后继续 工 作 ，Δt=φi+tin；（2） 检 测 系 统 状 态m+1≤i≤n，进行预防性维修，Δt=φi+tin+tma；（3）检测系统状态i=n+1，系统失效替换如新，Δt=φi+tin+tre；

5）报酬空间:即费用空间，包括系统检测费用、预防性维修费用、因检测或失效造成的停机损失、系统更换费用；

6）决策准则:当系统长期运行时，即t→∞，平均费用率最低，稳态可用度As大于a*s。

该半马尔可夫决策过程模型状态空间S离散，各状态i下的行动集A(i)有限，故存在最优的平稳策略。

假设Π为该模型维修策略平稳决策集，策略f 是 S→A(i)的 映 射 ，则 f=(f(i)=(a,φi)∈A(i))i=1,…,n+1，其中i∈S 。

令 t(f)=diag[t(i,f(i))]n×n，其中 t(i,f(i))是决策过程的策略 f下在状态i停留的时间，i=1,…,n。

令 r(f)=diag[r(i,f(i))](n+1)×(n+1)，其中 r(i,f(i))是决策过程的策略 f下在状态i的费用。则该半马尔可夫决策过程模型可简化为{S,A(i),pij(f(i)),t(i,f(i)),r(i,f(i)),V|i,j∈S,f(i)∈A(i)}。

5 模型建立与分析

5.1 系统状态转移矩阵

假设在某一时刻，单部件系统处于状态i的x位相，若两次相邻检测间经受了冲击则处于状态(i,j)的x位相，检测工作、维修台预防性维修工作以及系统更换工作的位相分别表示为Y(t)、Z(t)、J(t)。系统是否经受过冲击只有通过检测才能发现，同时随着时间推移系统不断退化。根据系统部件状态转移规律以及检测和维修更换模式，可将系统划分为11个不同状态，表示为Ω={H0,H1,H2,H3,H4,H5,H6,H7,H8,H9,H10}，具体含义如下。

H0={i,x,y(t);2≤i≤m,1≤x≤hi,1≤y(t)≤f}表示通过检测得出系统部件经历了退化，无外部冲击，处于完好状态，系统正常运行，不进行预防性维修；

H1={(i,j),x,y(t);1≤j≤ρ,2≤i≤m,1≤x≤hi,1≤y(t)≤f}表示通过检测得出系统部件经历了退化和外部冲击，处于完好状态，系统正常运行，不进行预防性维修；

H2={i,x,y(t);m+1≤i≤n,1≤x≤hi,1≤y(t)≤f}表示通过检测得出系统部件经历了退化，无外部冲击，处于劣化状态，需要进行预防性维修；

H3={i,x,z(t);m+1≤i≤n,1≤x≤hi,1≤z(t)≤l}表示系统部件经历了退化，无外部冲击，处于劣化状态，根据检测结果对其进行预防性维修；

H4={(i,j),x,y(t);1≤ j≤ρ,m+1≤ i≤ n,1≤x≤hi,1≤y(t)≤f}表示通过检测得出系统部件经历了退化和外部冲击，处于劣化状态，需要进行预防性维修；

H5={(i,j),x,z(t);1≤j≤ρ,m+1≤ i≤n,1≤x≤hi,1≤z(t)≤l}表示系统部件经历了退化和外部冲击，处于劣化状态，根据检测结果对其进行预防性维修；

H6={i,x,y(t);i=n+1,1≤x≤hi,1≤y(t)≤f} 表示通过检测得出系统部件经历了退化，无外部冲击，处于失效状态，需要进行更换；

H7={i,x,z(t);i=n+1,1≤x≤hi,1≤z(t)≤l} 表示系统部件经历了退化，无外部冲击，处于失效状态，根据检测结果对其进行更换；

H8={(i,j),x,y(t);1≤j≤ρ,i=n+1,1≤x≤hi,1≤y(t)≤f}表示通过检测得出系统部件经历了退化和外部冲击，处于失效状态，需要进行更换；

H9={(i,j),x,z(t);1≤j≤ρ,i=n+1,1≤x≤hi,1≤z(t)≤l}表示系统部件经历了退化和外部冲击，处于失效状态，根据检测结果对其进行更换；

H10={i,x;i=1,1≤x≤hi}表示系统处于全新状态，无退化和外部冲击影响。

根据系统状态空间划分，为便于表示系统状态转移，可将Pij、Dij以及Oik根据系统部件不同状态表示如下:

其中，P2、P3分别表示系统在完好状态、劣化状态内部转移的概率矩阵，P12、P13分别表示系统从全新状态向完好状态、劣化状态转移的概率矩阵，P23分别表示系统从完好状态向劣化状态转移的概率矩阵，P1(n+1)，P2(n+1)、P3(n+1)分别表示系统从全新状态、完好状态、劣化状态向失效状态转移的概率矩阵，D同理亦然。

根据划分的11个状态空间，构建状态转移图如图2。

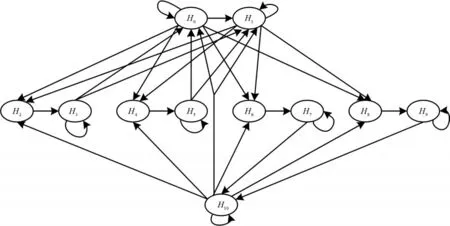
图2 系统状态转移图

下面根据系统状态转移图对其状态转移情况进行说明。

1）各状态空间内部转移分析

H0内部转移:该转移为系统部件自身转移。系统部件均处于完好状态，其内部转移存在两种情况:在水平i（2≤i≤m）的内部转移，转移矩阵为diag(T2,…,Tm)；从 水 平 i进 入 水 平 j（ 2≤i＜j≤m ）的转移，矩阵为 diag()P2diag(α2,…,αm)。令矩 阵 为 diag(T2,…,Tm)⊗diag()P2diag(α2,…,αm)，阶数为 ρgfh*。

同理可得:

H1内 部 转 移 矩 阵 为 diag(T20,…,Tm0)D2diag(α2,…,αm)⊗W0λ⊗Igf，阶数为 ρgfh*；

H3内部转移矩阵为 S⊗Iρf(n-m)，阶数为ρ(n-m)fl；

H5内部转移矩阵为 S⊗Iρf(n-m)，阶数为ρ(n-m)fl；

H7内部转移矩阵为B⊗Iρf，阶数为 ρfv；

H9内部转移矩阵为B⊗Iρf，阶数为 ρfv；

H10内部转移矩阵为 T1⊗Iρfg，阶数为 ρgfh1；

H2、H4、H6、H8的内部转移矩阵均为0。

2）不同状态空间转移分析

从H0到H1的状态转移:系统被检测出经历了退化和外部冲击，但依然处于完好状态，转移矩阵为Q01=U0⊗δ⊗diag(T20,…,Tm0)D2diag(α2,…,αm)⊗W0λ⊗R0⊗ζ，阶数为 ρgfh*；

从H0到H2的状态转移:系统被检测出经历了内部退化，从完好状态退化到劣化状态，转移矩阵 为 Q02=U0⊗δ⊗diag(T20,…,Tm0)P23diag(αm+1,…,αn)⊗Iρf；

从H0到H4的状态转移:系统被检测出经历了退化和外部冲击，从完好状态转移到劣化状态，转移矩阵为Q04=U0⊗δ⊗diag()D23diag(αm+1,…,αn)⊗W0λ⊗If；

从H0到H6的状态转移:系统被检测出经历了内部退化，从完好状态退化到失效状态，转移矩阵为Q06=U0⊗δ⊗diag()P2(n+1)⊗ Iρf；

从H0到H8的状态转移:系统被检测出经历了退化和外部冲击，从完好状态转移到失效状态，转移 矩 阵 为 Q08=U0⊗δ⊗diag()D2(n+1)⊗W0λ⊗If；

从H2到H3的状态转移:系统被检测出处于劣化状态，需要进行预防性维修，检测结束进入维修工作，转移矩阵为Q23=R0⊗θ⊗Iρf(n-m)；

从H3到H0的状态转移:对系统进行不完全预防性维修后由劣化状态返回到完好状态，转移矩阵为[Q30Q31]=[S0⊗O32diag(α2,…,αm)⊗ ζ⊗ Iρf0] ；

同理{H0,H1,H2,H3,H4,H5,H6,H7,H8,H9,H10}中各个状态之间的转移矩阵如下:

结合PH分布的定义，根据上述对系统状态转移的分析，就可得出系统转移矩阵Q如下:

5.2 转移时间

系统在两相邻检测之间的转移时间包括检测间隔时间、检测时间、维修时间和替换时间，决策点为系统开始本次检测的时间点，则从本次决策点到下次决策的平均决策间隔时间可表示为

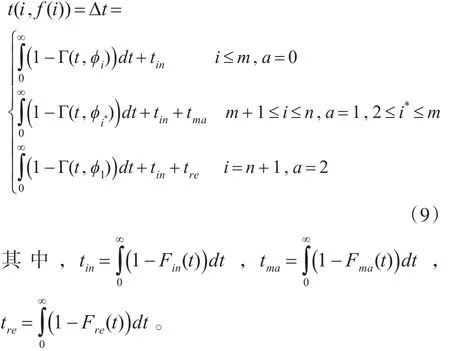
5.3 系统稳态可用度与费用函数

系统稳态可用度就是系统处于工作状态下的稳态概率，即系统停留在状态集H0∪H1∪H10的稳态概率。系统在经历长时间运行之后会进入稳定状态。当系统处于稳态时，其各状态在相互转移的过程中停留在每个状态的概率可以构成稳态概率向量 π ，与各状态相 对 应 可分解为 π=(π0,π1,π2,π3,π4,π5,π6,π7,π8,π9,π10)，根据稳态概率向量的相关性质可知其满足下列方程组:

故系统稳态可用度As可表示为

系统费用函数包括从现决策点到下次决策的系统检测费用、预防性维修费用或系统更换费用、因检测或失效造成的停机损失费用。根据现决策点系统所处状态，考虑系统同时受到内部退化和外部冲击进入失效状态的概率较大，可将系统费用函数表示为

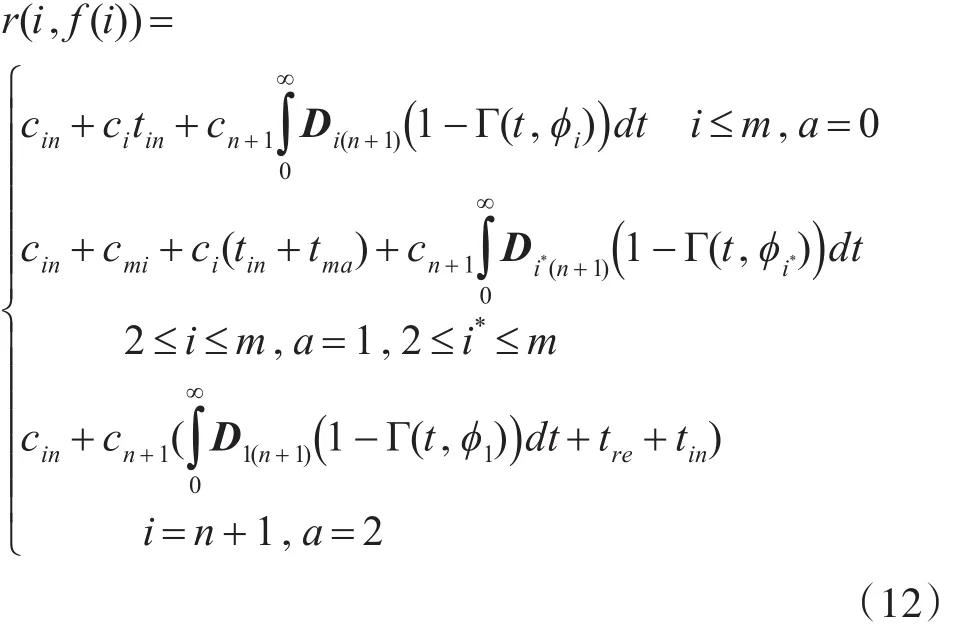
其中，i*为系统在状态i经过不完全预防性维修所返回的状态，找出状态i对应的Oij矩阵第i行中的最小值，其所对应的列即为状态i*所对应的列。

5.4 决策准则

根据决策准则的相关要求和模型假设，可以看出劣化部件在有限时间内不会发生无穷多次状态转移，从而建立最优方程。PH分布在非负半轴上可近似拟合其他随机分布，其将状态i划分为hi个相位i"，根据系统状态空间S将系统各状态相位集设为S"={s"}i=1,…,n+1={(1,…,h1),(h1+1,…,h2),…,(hn+1,…,hn+1)}，而各相位仅具有概率意义，并无实际物理意义。因此一个状态i下hi个相位所做出的维修决策应一致才符合实际情况，故可先建立系统长期运行平均费用率最低的最优方程为

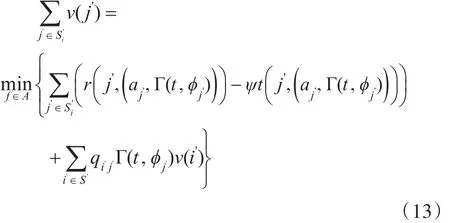
同时，决策目标函数为系统长期运行平均费用率最低且稳态可用度As大于。在迭代计算的各步所得维修策略的基础上，根据所得的检测间隔时间数值进行拟合，表示为PH分布形式，带入状态转移矩阵求解计算稳态概率向量得出稳态可用度判断其是否满足要求，再进行下一步迭代，直至两者同时达到最优，具体流程见图3。

图3 最优决策求解思路图

6 模型ε-最优平稳策略

6.1 半马尔可夫决策过程的转化

为了便于求解计算，一般将半马尔科夫决策六元组转化为马尔科夫决策五元组。针对于该模型，可将转移时间与报酬函数相结合合二为一，转化为马尔科夫决策五元组，具体分析如下。

根据系统两决策点间的转移时间公式可以看出，必存在正常数κ，使得则令t*=1 κ，可转化马尔科夫决策五元组如下:

{S,A(i),pij(f(i)),r˜(i,f(i)),V|i,j∈ S,f(i)∈ A(i)}

故系统长期运行平均费用率最低的最优方程可转化为

6.2 值迭代算法

为了求解最优方程XX，得出ε-最佳平稳策略，采用值迭代算法，下面对具体步骤做进一步描述。

步骤1:初始假设

任取迭代初值v0(j")，给定ε并且置n=0；

步骤2:选择策略 f0

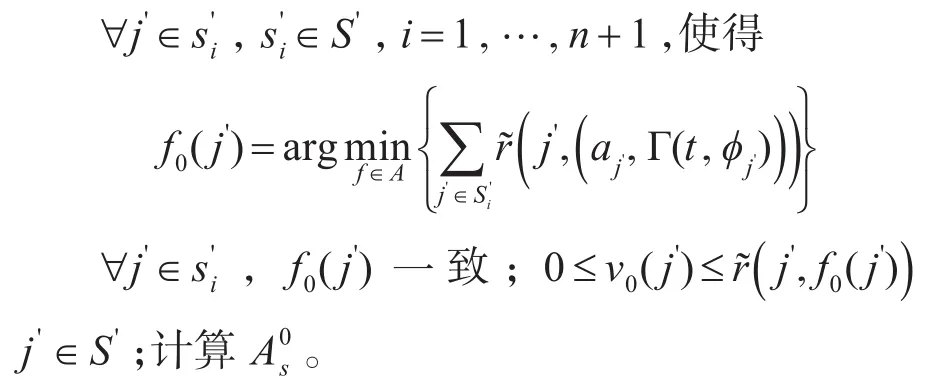
特别地，当i=n+1时，对应策略为(a=2,Γ(t,φ1)) 。

步骤3:计算vn+1(j")

步骤4:最优判断

算法停止；否则将n增加1，转入步骤3。

7 算例

该算例包括两部分:1）根据模型问题描述，假设该单部件系统状态可划分为6个，各状态停留时间分别服从不同的PH分布，建立不完全预防性维修优化模型，通过值迭代算法求解计算得出ε-最佳平稳策略，验证模型的正确性与适用性；2）分析费用参数cin变化对最佳策略的影响，证明随机检测的良好特性。

7.1 模型正确性、适用性验证

假设该单部件系统具有6个不同状态，其中{6}表示系统处于失效状态，6个状态的所分别对应的检测间隔时间为确定性数值，可拟合为PH分布，有g阶PH表示(ζ,U)，且检测时间、不完全维修时间、系统替换时间忽略不计。系统检测费用、预防性维修费用、系统更换费用以及因失效造成的停机损失费用分别为cin=1、cm4=6、cm5=8、cr=12、cn+1=10，则系统在各状态的停留时间以及随机冲击到达过程的PH表示如表1。

另:

根据上述假设条件，建立系统状态转移矩阵，采用上述的值迭代算法，令ε=1×10-4，稳态可用度As大于0.97，经过63次迭代，可得出满足终止原则的迭代结果，如表2所示。

由表2可以看出，经过63次迭代，可得出优化维修策略，此时，系统平均费用率最低为0.1025，稳态可用度As=0.9839，满足决策准则，验证了模型的正确性和适用性。

7.2 模型费用参数变化对维修策略的影响

在上节算例的基础上，增加cin，分析系统各状态最佳检测间隔时间的变化，如图4所示。

表1 系统各状态停留时间以及随机冲击到达过程的PH表示

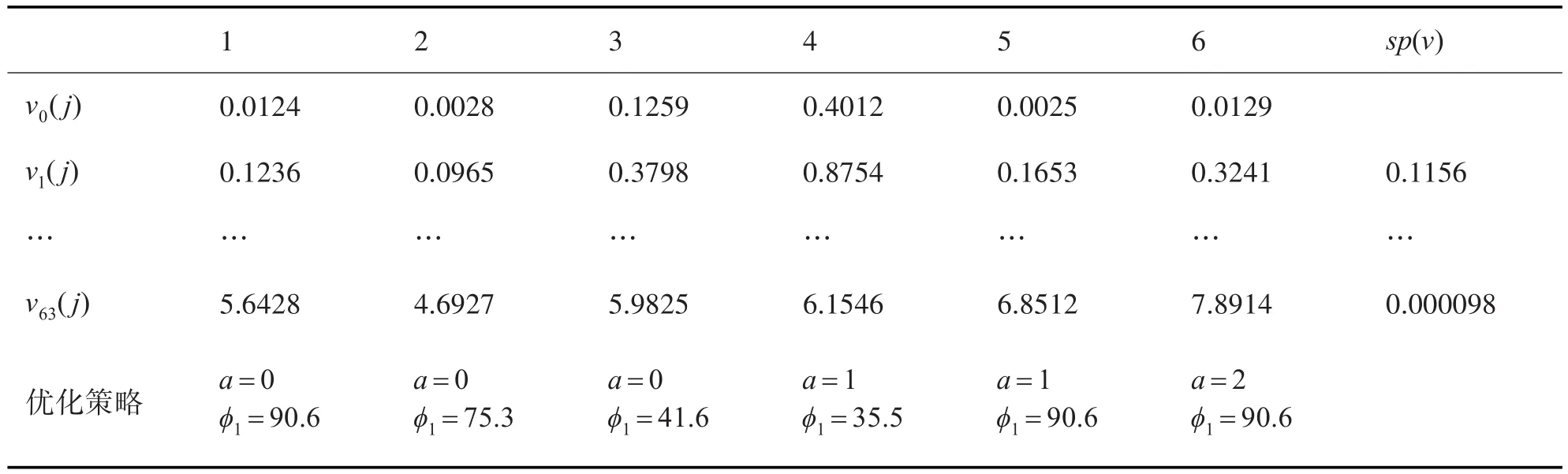
表2 迭代过程相关数据

图4坐标轴横坐标为检测费用cin的变化，系统部件各个状态均需检测得出，因此从图中可以看出，当检测费用在整体费用中所占比例越来越大时，检测间隔随之提升，这是由于最优策略目标是达到系统平均费用率最低，为减少费用，需增加检测间隔，降低检测次数。同时，当cin=5时，与预防性维修费用一致，此时为了减少费用，应当降低预防性维修控制阈，将状态3和状态4合为同一劣化状态，这样既提高了预防性维修效果，又可减少检测次数，从整体上降低了平均费用；当cin=8时，与换件维修费用一致，为了减少费用可将状态3、4、5看做一个状态。

图4 检测费用变化对维修策略的影响

8 结语

本文以考虑随机冲击的单部件退化系统为研究对象，系统内有单一维修台，可进行不完全预防性维修和换件维修两种维修活动，维修活动由随机检测结果决定，将系统性能划分为多个离散状态，建立了基于PH分布的系统维修策略优化模型，利用值迭代算法，确定了系统最佳的预防性维修控制阈和各状态对应的检测间隔时间，以达到长期运行条件下的平均费用率最低且系统稳态可用度满足要求。最后，通过算例进行了63次迭代得出了最优策略，验证了模型的正确性与适用性，同时演示了检测费用参数变化对最佳策略的影响，具有一定的工程实践价值。