基于扇形优化Dijkstra算法的舰船最佳导航路线分析∗

田茹会

（陕西能源职业技术学院 咸阳 712000）

1 引言

舰船作为一个危险的工作场所，一旦出现不规范作业或受海上因素的影响便可能造成无法挽回的巨大损失［1～4］。如果现场人员能够在遇到灾害时快速选择最优路径导航，则可以显著提升生还概率［5］。由此可见，采用合适的方法来求解得到最佳路线已经成为一项具有重大现实意义的课题。

采用传统Dijkstra算法来搜索最佳路径存在较大的盲目性，王玉琨［6］等利用经过扇形优化的Dijkstra算法来求解路线，使搜索速度获得显著提高；同时，杨林［7］在研究煤矿瓦斯事故的应对方案过程中，对导航实施“当量计算”并采用Dijkstra最佳路径算法求出最佳导航路径。王磊等采用Dijsktra算法来完成对路径的导航分析功能，同时粒子群算法来规划真实路径的选择过程，通过为指定节点区域确定较优路径来实现路径规划的目的。薛峰会等研究了对船舶导航路径计算过程进行优化的方法，以Dijkstra算法优化了航行规划图上所有节点之间的航行路径。本文根据以上研究结果，对导航当量长度以及导航速度进行了深入探讨，并通过Dijkstra算法构建得到了选择舰船最佳导航路线的模型。

对导航当量长度以及导航速度进行了深入探讨，给出了扇形优化Dijkstra算法进行分析流程，并进行了应用示例。

2 导航当量长度

选择Dijkstra算法来求解最佳导航之前，应先把所有导航表示成统一的当量长度。先根据舰船导航中的实际网络状态及其影响程度来得到各个导航对应的影响因子。之后，考虑到海上作业环境具有较大的复杂性与特殊性，因此实际导航影响因子会受到多种因素的共同影响，本文将从以下各个角度对导航速度进行分析，包括导航有效宽度、高度、风向、风速及其水流速程度。针对上述各项影响因素，依次采用系数α1、α2、α3、α4、α5进行表示，并得到下述表达式［8］

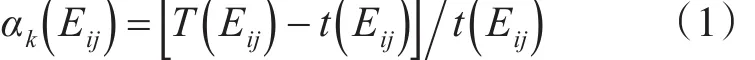
在式（1）中，Eij代表连接节点 i与 j的导航；α(Eij)是导航Eij中包含的影响因子系数；T(Eij)是包含此该影响因子的情况下经过导航Eij所需的时间，单位s；t(Eij)是不包含此影响因子时经过导航Eij所需的时间，单位s。

导航Eij综合影响程度系数α(Eij)取决于所有因子影响程度系数进行加和所得的结果，表示为如下的形式:

采用统一测试条件完成现场模拟与实测过程，并对T(Eij)与t(Eij)测试结果进行取平均，结合式（1）求解出对导航具有影响的各个因子系数，之后计算得到影响因素的系数之和，再通过式（2）求解得到导航的综合影响程度系数。

当导航的影响因子被确定之后，则可以根据导航真实长度与总影响程度系数来获得当量长度，表达式如下:

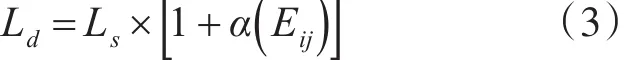
从上式中可以看到，Ls是对导航进行实际测试所得的长度，单位m；Ld代表导航当量长度，单位m；α( )

Eij代表导航总影响程度系数。以同样的条件进行现场模拟测试与仿真，经多次测试得到的Ls平均值，再通过式（3）计算导航当量长度。计算连接受灾地点与避难地点之间的各个可通行导航对应的当量长度，并寻找具有最小当量长度的路径，再以此路径作为最佳导航路径。

3 扇形优化Dijkstra算法

采用传统Dijkstra算法进行处理时，是先选择一个中心位置再通过不断增加节点距离的方式得到最佳路径的搜索算法，需完成各个标定路线的搜索之后才可以进行统计运算，实际计算量非常大，因此导致搜索速度明显变慢，同时也使得搜索过程变得更加盲目。为了克服Dijkstra算法的以上缺陷，本文选择经过扇形优化的Dijkstra算法进行分析，经过优化后的Dijkstra算法所采用的核心处理思想是按照人员定位结果来得到舰船导航的源点，根据设定的导航目标点以直线连接的方式得到由轴线组成的扇形区，再对该区域进行搜索得到最佳路径。由此实现稳定运行与快速搜索的目的，可以更好地适应舰船导航中的复杂网络环境。

图1 Dijkstra算法流程图

从图1中可以看到采用扇形优化Dijkstra算法进行分析的流程，具体步骤如下:

1）从舰船导航网络内选择出起点V1以及终点Vn，在此基础上求得最佳扇形区；

2）临时标记图中的各个起点Vi，分别以二个坐标来表示各节点，其中，第一个坐标是节点对应的母节点，即与最佳路径相邻的之前节点，第二个坐标对应的是此节点与起点V1之间的距离权值；把V1标记成（1，0），再以（1，D1i）来表示其它节点Vi，若果Vi与V1之间是保持直接相连的状态，则可以得到D1i=L1i，如果Vi与V1之间不是保持直接相连的状态，则此时D1i=∞，同时将V1归入永久标记点组成的集合S=｛V1｝；

3）对比分析集合T=V-S内各个没有被标记的点对应的权值选，从中选出具有最小权值的点Vk作为永久标记点，此时可以得到S=｛V1，Vk｝，和永久标记点Vk之间保持直接相邻状态的各个点Vi，当满足条件 D1k+Lki＜D1i时，存在 D1i=D1k+Lki，此时母节点将转变成Vk；

4）重复执行以上各个步骤到终点Vn为止，得到的D1n是最优路径权值和，由终点母节点往回追溯，便可得到这一最优路径。

4 应用示例

从图2中可以看到对舰船的局部导航进行模拟所得的网络，可以发现节点①代表航船的实际位置，节点⑨是导航目标位置。求解由节点①与节点⑨之间的最佳路径，确保这一路径是各个可行路径中能够实现最佳通行时间的导航。

图2 舰船局部导航模拟网络图

为海上作业人员提供的启动后根据实际型号的差异实际可用时间介于25min～40min范围内。因此，海上作业人员需确保能在的有效工作时间中导航到安全的避难位置。根据以上分析，本文将有效时间设定为25min，相当于所有作业人员到达最近安全区域的时间不能超过25min。

针对本模型舰船的真实情况，分别为节点3与节点6，并以此作为人员导航的安全目标位置。而且给其他各个节点人员到节点13需要的时间都大于25min，所以其他各节点的海上作业人员应在限定时间内转移至别的安全位置点。

可以作为导航安全位置的节点包括节点3、6、13与17，之后再通过Dijkstra算法求解出从舰船模型内的各节点导航至上述安全位置点需要消耗的时间以及寻找最佳导航路径。从表1中可以看到由本文舰船模型的20个节点导航至节点3、6、13与17对应的时间。

表2是根据海上局部导航图各参数进行计算所得的结果，可以看到每次搜素时得到的最小导航当量。其中，最佳导航路径是①②⑤⑧⑨。

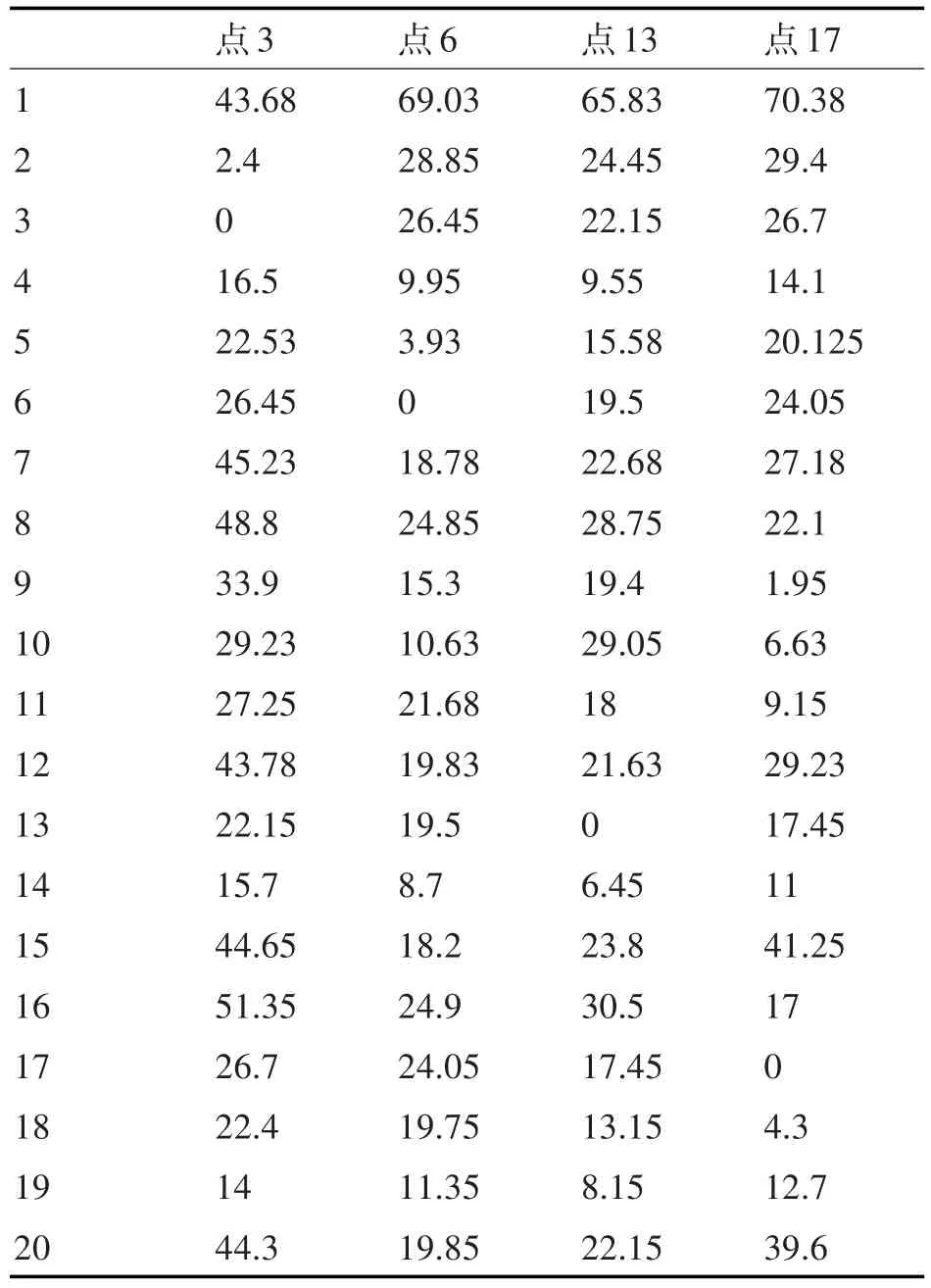
表1 节点导航时间表

表2 导航参数表

基于Dijkstra算法得到的K则最优路径双向搜索算法可以得到多条最佳导航路径，本文选择其中的两种最佳导航路径，结果见表3。

根据表3可知，当出现安全事故时，作业人员可通过最近安全避难点进行导航。

选择VSL进行最佳路径编程并演示海上导航培训系统运行过程，其中该程序的脚本图可以读取导航当量长度与人员导航速度，同时根据Dijkstra算法求出最佳导航路径，形象展示导航过程。

表3 最佳导航路径表

先在Virtools内创建VSL脚本程序，如果发现脚本图内存在不同的VSL脚本程序时则对其进行更名，从而准确分辨各VSL脚本程序的功能。再结合实际需求设定bIn/bOut端口与pIn/pOut参数的种类与数量。

先通过VSL脚本程序创建得到一个存储表来保存当量长度与导航速度。创建Run VSL并将其更名为Laneway Data Array，再把存储导航参数的代码输入编程栏进行调试。

之后，以VSL脚本程序进行编程并求解出最佳路径，构建一个Run VSL并将其更名为Get Shortest Path。选择VSL来编写Dijkstra算法时，通过优化改进处理可以降低搜索过程的遍历节点个数，使程序高效运行。

最后，以系统BB模块依次和通过VSL脚本程序编译的Laneway Data Array模块以及Get Shortest Path模块进行连线得到脚本图。

在系统的操作界面中，点击选择系统的演示功能，从图2选择节点①作为受灾位置，再点击系统的演示按钮，可以看到此时系统的人物开始演示导航的过程，并可以得到导航所需的最佳路径及时间。

根据本实验测试结果可知，利用VSL编程以及把Dijkstra算法应用于海上导航模拟系统是完全可行的。

5 结语

对导航当量长度以及导航速度进行了深入探讨，给出了扇形优化Dijkstra算法进行分析流程，并进行了应用示例。研究结果得到:

1）基于Dijkstra算法得到的K则最优路径双向搜索算法可以得到多条最佳导航路径，本文选择其中的两种最佳导航路径，完全满足避难需求。

2）选择VSL进行最佳路径编程并演示海上导航培训系统运行过程，根据Dijkstra算法求出最佳导航路径，形象展示导航过程。利用VSL编程以及把Dijkstra算法应用于海上导航模拟系统是完全可行的。