分簇路由算法中的多跳跳数及中继节点优化
2019-06-06王亚刚
孙 振,王 凯,王亚刚
1(上海理工大学 光电信息与计算机工程学院,上海 200093)2(上海理工大学 上海出版印刷高等专科学校,上海 200093)
1 引 言
无线传感器网络WSNs(wireless sensor networks)是由随机部署的微型传感器节点组成,通过无线方式与终端用户通信,监测多种物理参数和执行命令动作的多跳自组织网络[1].WSNs被广泛应用于军事、环境观测等领域,但由于大部分应用情景中采用能量有限的电池供电,使得网络生命周期较大程度受到电池能量的制约[2].节点网络层中的路由协议是节能和均衡负载的关键技术之一,因此如何设计能量高效的路由协议至关重要[3].
为了节省能耗,学者们提出许多利用数据融合技术减少数据传输量的层次路由协议,而在层次路由协议中,分簇路由算法较为活跃、有效[4].LEACH[5]算法是早期经典分簇算法之一,LEACH算法按轮循环,以概率选取簇头,然后根据入簇信号的强度入簇,最后簇头直接将融合后的数据发给基站.LEACH算法的主要缺点是:a)剩余能量低的传感器节点也会出任簇头;b)采用单跳传输造成距基站较远的节点过早死亡.为改进LEACH算法的单跳不足,EBCRP[6]算法综合考虑邻近簇头的距离和方向来选择中继簇头,实现簇间多跳传输,节省了远基站簇头能量,但没有考虑中继簇头的剩余能量,造成簇头过早死亡.针对多跳虽能够节省能量,但易造成近基站节点过早死亡的热区[7]问题,学者们提出了EEUC[8]、DEBUC[9]、SNNUC[10]等算法,EEUC通过竞争半径调节簇规模,近基站簇的簇规模较小,从而减少了簇内能耗,簇头将有更多能量承担路由传输任务.DEBUC算法基于EEUC算法的竞争机制,利用节点剩余能量调制等待时间竞选簇头,节省了节点信息交换能耗,有效延长网络寿命.SNNUC算法基于时间成簇,利用竞争半径调节簇规模时,将节点密度、剩余能量考虑在内,使簇的大小更加合理.此外,还有一些非均匀分簇算法通过竞选区头[11]或者副簇头[12]来分担簇头的能耗,有效的平衡了节点间的能耗.上述非均匀分簇算法存在待改进的地方,如:a)热区状况的评价较为粗糙,大部分算法只整体观测到越靠近基站的区域越‘热’,而且无法对热区“热”的程度进行量化;b)多跳传输数据时,将源节点到中继,中继再到基站两跳的最低能耗作为选择中继的标准,但能耗最低时的跳数不一定为两跳.关于一定距离能耗最低的最优跳数有关讨论中,文献[13]推导出最优跳数的通项,但此通项推导过程中未对平均跳距处于自由空间模型和多路径衰减模型各自的最优整数跳数进行比较,而文献[14]只精确分析了以一跳为最优跳数和以两跳为最优跳数时节点距基站的距离,需要再推广分析.
针对以上问题,本文提出了一种基于最优跳数的非均匀分簇路由算法(下文简称UCOH算法).主要特点如下:a)利用推导出的路由理想路径引入支撑量,量化区域“热”的程度,以优化簇的规模,进一步均衡簇头节点的簇内和簇外消耗;b)限制成簇区域以及利用基站广播公共信息,节省近基站节点整体能耗和节点信息交换能耗;c)数据传输阶段,在本轮的候选簇头中选择中继节点,以减少簇头负载.下一跳中继节点的评价考虑了最优跳数的跳距,剩余能量,传输方向,期望在保持能耗平衡的同时减小多跳能耗.实验结果表明,对于密度较大的网络,本算法与DEBUC、UCDP、SNNUC相比,能使以30%节点死亡为网络失效的网络生命周期得到不同程度的延长.
2 系统模型
2.1 网络模型
在文献[10]的基础上,假设传感器网络模型的属性为:
a)传感器节点是同构的,即有相同的初始能量,处理能力等.
b)传感器节点具有唯一标识ID,且位置静止,节点能够感知基站的方位.
c)传感器可以获得自身剩余能量值和通过数据包获知其他节点剩余能量值.
d)传感器节点的发射功率可调,各个节点能够相互进行通信并且每个节点能与基站直接进行通信.
e)基站能量不受限制且处理能力,存储能力强大,发射功率可覆盖所有节点,能获得网络边界.
2.2 能耗模型及最优跳数的推导
本文采用与文献[15]相同的一阶无线电模型,重点考虑数据传输和接收时所消耗的能量,忽略节点采集数据、计算、存储等过程中消耗的能量.节点发送lbit数据至相距距离为d的节点所消耗的能量为:
(1)
节点接收lbit数据的能耗为:
ERx(l)=lEelec
(2)
其中:Eelec=50nJ/bit为射频能耗系数;εfs=10pJ/bit/m2,εmp=0.0013pJ/bit/m4分别为自由空间模型和多路径衰减模型功率放大电路能耗系数;d0为距离阈值,本文设为87.7m.
下面推导节点直线发送数据到基站的最优跳数.
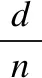
定义1.当节点到基站的距离为d,若从节点经n跳直线传输数据到基站时各节点所耗能量和最小,则称n跳为节点向基站传输数据的最优跳数.
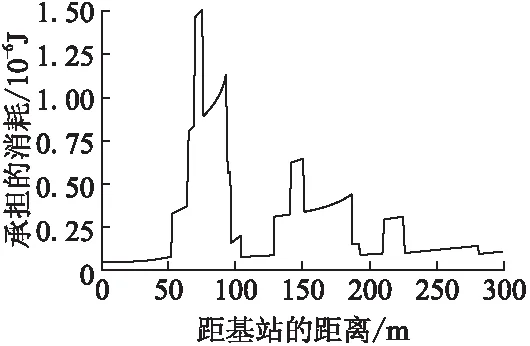
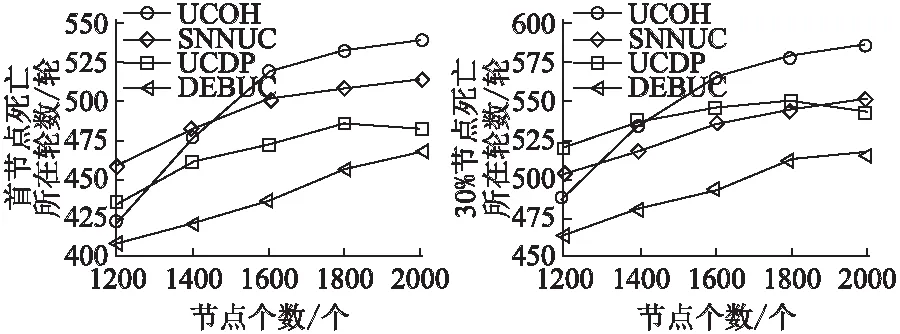
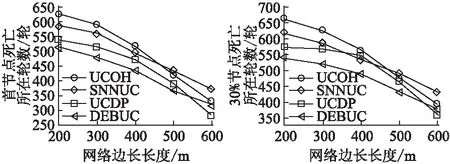
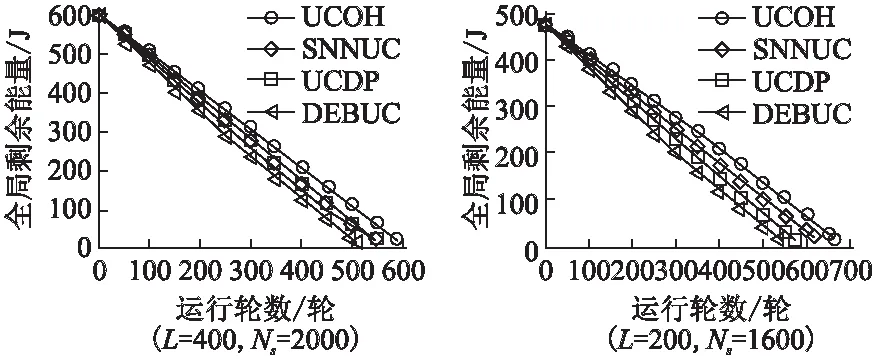
推论1.若节点将数据经中继直线传输到基站,节点到基站距离为d,当dc(n) (3) 当给出节点到基站的距离时可用hop(d)计算最优跳数,其计算公式为: (4) 「⎤表示向上取整. (5) 以n为自变量,假设n连续,则上式对n求导为: (6) 图1 简单线性网络Fig.1 Simple linear net (7) 令Δ(d)≥0,据以上分析,解出式(8). (8) 于是得出当nd0 采用数据融合技术有利于减少发送的数据量,本文的融合模型为:簇内数据完全融合,并且认为簇间数据差异较大而不进行融合,融合能耗设定为EDA=5nJ/bit. 总的来说,UCOH算法是一种结合轮循环机制、非均匀时间竞争分簇机制、数据融合以及数据多跳传输的算法.轮循环机制是指系统按轮运行,每轮分为:a)轮初始化阶段,首轮时,各节点根据自身到基站的最优跳数确定自己的分区,并确定成为簇头时的入簇半径(用于控制簇的规模).首轮后,基站在每轮的此阶段广播必要的信息;b)非均匀时间竞争成簇阶段,此阶段网络首先竞选候选簇头,然后根据剩余能量调制时间竞争簇头,最后普通节点根据入簇半径、簇头剩余能量和路由消耗进行入簇;c)数据传输阶段,首先普通节点将数据单跳传给簇头,簇头融合数据后将数据或者直接发送给基站,或者选择剩余能量高并较符合最优跳数跳距的候选节点多次中继后发给基站. 要特别说明的是,在成簇阶段,文献[16]使距基站小于87.7m的节点不成簇入簇以节省分簇和簇内通信损耗,但未给出理论依据,本文使距基站小于74m的候选节点不竞选簇头,普通节点距基站小于74m时不入簇以防止成簇的节能效益不如不成簇.依据如下:如存在节点Si和簇头Sj两节点距基站距离都小于d0,且两节点的距离小于d0,则节点Si直接发送lbit数据到基站的消耗和经簇头中继发送的消耗分别为Edirect,Ec_relay,如式(9),(10)所示. Edirect=ETx(l,dis) (9) Ec_relay=ETx(l,dij)+ERx(l)+lEDA+ETx((1-pDA)l,djs) (10) 其中:pDA表示数据融合率;dis,djs,dij是两节点到基站的距离和两节点之间的距离.如果期望入簇会节省能量需要Edirect>Ec_relay,将其展开如式(11)所示. (11) 为简单起见,假设数据完全融合则pDA=1,而dij≥0,经计算得dis至少在74m以上时,上式才有可能成立.对于其他位置的节点,按照经典正常成簇入簇,因此本文以74m为成簇分界线. 下面给出其他相关定义. 定义 2.支撑量 假设节点均匀分布,每个节点都有符合最优跳数的中继,则支撑量src(dtoBS,dtoBS-max)表示以最优跳数的路径传输数据时,基站某方向射线上距基站dtoBS的位置所承担的最大消耗(实际节点密度可能不这么高),用于表示多跳传输时某位置‘热’的程度.其公式如式(12)所示. rc(ms,mr,dtoBS,dtoBS-max) (12) rc(ms,mr,dtoBS,dtoBS-max)= (13) 其中:rc(ms,mr,dtoBS,dtoBS-max)表示数据源自所处ms区,当以最优跳数传输时,在mr(mr=1,2,3,…,ms)区(最优跳数形成的路径会经过朝向基站的每一个区)距基站dtoBS的节点收发数据所耗的能量;dtoBS-max为从基站发射的沿某方向的射线与网络边界交点到基站的距离,也既该射线方向dtoBS的最大值.rc(ms,mr,dtoBS,dtoBS-max)公式如(13)所示.假设dtoBS-max=300,则以dtoBS为自变量src(dtoBS,dtoBS-max)的曲线为图2所示,从图中可以看出簇外能耗情况类似波浪并非线性地与节点距基站的距离相关. 图2 dtoBS-max=300支撑量分布情况Fig.2 Distribution of src when dtoBS-max=300 定义3.最优前向路由消耗frc(dtoBS) 用来表示距基站dtoBS的节点,以最优跳数发送1bit数据所耗能量,公式如式(14)所示. (14) 下面将按轮循环机制详细介绍本算法. 首轮时,在节点部署完毕后,基站会发送一个“hello”消息至网络中的所有节点,节点Si根据接收到的信号强度大小估算自身到基站的距离dis,确定自己所属分区,区号等于hop(dis),以表征各节点最优跳数特征. 为竞选出均匀分布的簇头,距基站小于74m的节点不竞选簇头,竞争半径为0,距基站大于74m的节点赋予相同的竞争半径Rcmp.为避免热区内的节点因簇外数据传输任务过重而能量耗尽,为每一个节点设置一个入簇半径,以调节节点出任簇头时所在簇的规模.簇头节点Si的簇内能耗主要为接收簇内节点数据消耗,簇外能耗主要体现在支撑量上(两者为估计值,后面节点要根据实际能耗情况入簇),假设节点均匀分布,若要通过减少簇内能耗供中继使用有: (15) 其中:NS为节点数量;S为网络面积,则等式左边为预计缩小入簇半径时预留给中继使用的能量,其在一定程度上反映了节点密度信息;Ri为簇头Si的入簇半径;dborder-i为基站沿节点Si方向的射线与边界的交点到基站的距离(本文假设基站在网络中央),将Ri解出有: (16) 通常而言发挥入簇优势时,簇内耗能会比簇外耗能要大,则上式衡有解,且上式表明,较热区域内的节点会被分配较小的入簇半径,以平衡节点成为簇头后的簇内簇外路由能耗.该式综合了簇内簇外的具体能耗,与同类算法比例化距基站距离等因素来调节簇规模相比要精确些. 首轮后,基站在这一阶段会广播CYCLE_START报文给所有节点,报文包括上一轮到基站距离大于74m的存活节点的平均剩余能量和存活节点数,这些数据由节点发送到基站的数据包中解析而来. 非均匀成簇的过程包括:选举候选簇头、簇头选举、普通节点入簇三个阶段.在前两个阶段中,考虑到一些应用基本信息大小与数据包大小之比较大或节点密度较大时,若节点相互交换基本信息总耗能会过大,故UCOH算法用基站广播最重要的公共能量信息成簇,而不考虑其他因素. 3.2.1 选举候选簇头 选举候选簇头时,首先各个节点依随机数(0-1)与阈值比较,若小于阈值则出任候选簇头,非候选簇头节点进入睡眠状态到簇头选举结束.所用的阈值公式改进自LEACH算法,对于节点Si来说其阈值函数如式(17)所示. (17) 3.2.2 簇头选举 UCOH算法在此阶段采用计时广播机制代替UCDP[11]算法协商机制来竞选簇头,以节省基本信息交换能耗. 对于距基站大于74m的候选簇头,计时广播机制让等待时间较短的候选簇头先广播获胜消息,邻居节点收到获胜信息则退出竞选.节点Si的邻居节点定义如式(18)所示. Di={Sj|Sj是候选簇首,且dij (18) 候选节点Si的等待时间ti改进自DEBUC算法,其公式如式(19)所示. (19) 簇头竞选完成后,各簇头以2倍d0为半径广播入簇报文CH_ADV_MSG,唤醒处于休眠状态的普通节点,该报文包括簇头的ID、入簇半径、距基站的距离和剩余能量,供普通节点判断加入哪一个簇更优. 3.2.3 普通节点入簇 为使簇内节点规模符合热区和平衡能耗,入簇方法如下:如果节点位于某些簇头的入簇半径内,则节点在那些入簇半径包含该节点的簇头中选择距离引力最大的簇入簇,如果节点不在任何簇头的入簇半径内,则节点在收到的入簇信息中选择信号强度最强的簇入簇,在网络生命周期后期,如果没有入簇信息,则将数据直接发送到基站.改进的距离引力具体化了UCDP算法中的距离因素,考虑了簇头的剩余能量、节点发送数据能耗和簇头最优前向路由消耗,公式如式(20)所示. (20) 其中:Si表示普通节点;CHj表示簇头;E(CHj)表示簇头的剩余能量;di-CHj表示节点Si和簇头CHj的距离.上式说明,普通节点会选择剩余能量较大,距离较近,并且前向数据传输消耗小的簇头,以均衡负载和降低能耗.选择好簇头后,节点发送JOIN_CLUSTER_MSG报文通知相应簇头.簇形成后,簇头会在簇内广播TDMA时隙,各节点按时隙通信.当簇头收集簇内数据并融合完毕后,进入数据传输阶段. 本算法采用簇内单跳和簇外多跳中继的数据传输方式,中继节点在候选簇头中选择.利用候选簇头作中继不会在竞选副簇头、区头上耗能,并防止如文献[17]收集源节点广播半径内所有节点的基本信息,导致信息收集耗能过多,节能效益反而降低的情形.下文将簇头或中继节点特定广播范围内的候选簇头称作该广播范围的邻居候选簇头(不包括本轮出任簇头的节点).传输策略总结如下: a)距基站74m以内的普通节点或中继将数据直接发送到基站; b)从图2可以看出距基站大于74m小于dc(1)的节点所处区域较热,应首要考虑能量平衡,所以将考虑是否继续中继,在该范围内的簇头或中继节点,以距基站的距离广播探测信息,在广播范围内的邻居候选簇头判断自己是否距基站更近并距基站小于74m,若是则将自己的基本信息发回簇头或中继节点(为使基本信息交换能耗不至过大,将在第4节整定候选簇头出任概率),簇头或中继节点Si构建每个邻居候选簇头Sj的信息表,如表1所示,用以寻找中继. 表1 节点Sj信息表Table 1 Information of node Sj 设Si邻居候选簇头集为Dn-i,则在节点集合 c)距基站大于dc(1)的簇头或中继节点Si以dc(1)为广播半径,以和上文类似的方式维护一个邻居候选簇头集合,首先,若邻居候选簇头Sj的剩余能量与Si探测到的所有邻居候选簇头平均剩余能量的比值小于一定比值,则不通过Sj中继,以保障能耗平衡,Sj比值公式Vj如式(21). (21) (22) g(dij)= (23) (24) (25) 以上公式中f(x1,x2)表示多跳比单跳所节省的能量差的比率0 算法 1.整体算法流程 Step1.如果是首轮,基站先广播“hello”报文,各节点根据式(4)、(16)计算区号和入簇半径.之后基站广播CYCLE_START报文. Step2.各节点根据式(17)出任候选簇头,并根据式(19)竞争簇头,普通节点根据3.2小节入簇策略入簇. Step3.距基站74m以内的普通节点(或之后中继)直接将数据发送到基站.簇头收集簇内数据并融合. Step4.对于距基站74m以外的每个簇头和中继候选簇头Si,Si发出探测信息获得Dn-i,若Dn-i为空,则将数据直接发往基站,否则:若Si到基站距离处于74到dc(1)之间,则从Droute中选取使dij最小的Sj做下一跳; 若Si到基站距离大于dc(1),选择Dn-i中能量梯度最大的且符合式(21)的节点做下一跳,没有符合条件的节点则将数据直接发送到基站.所有节点传输完毕,进入下一轮,转Step 1. 为了验证所提算法的性能,本文基于MATLAB 平台对DEBUC、UCDP、SNNUC、UCOH算法进行仿真,对比多项指标.假设传感器网络覆盖边长为L的正方形区域,基站位于区域中央,无线通信能耗模型的相关参数详见第2节,其他实验环境参数如表2所示. 表2 实验参数Table 2 Experimental parameters 候选簇头出任概率p的值在一定程度上影响着算法的性能,p过小不能发挥成簇的优势,p增大时虽然有更大概率找到符合最优跳数的中继候选簇头,但会在成簇阶段和路由阶段产生较大的信息交换能耗,本文通过实验分析确定本算法的最优p值.以L=400,NS=1600为例,调整p值(0.03-0.21)观测网络第一个节点、10%节点、30%节点死亡时网络运行轮数变化情况,得到如图3数据. 图3 节点死亡轮数变化曲线Fig.3 Variation curve of cycle of nodes death 从图3中可以看出:a)当p较小时,簇头数目较少,负载大,且一小部分节点入簇耗费能量较大,第一个节点死亡时间较早;b)当p再次增大时,节点入簇能耗和路由阶段节点构建路由表能耗增加,导致30%节点死亡的轮数提前;c)10%节点死亡后,其余节点成批迅速死亡,其原因一是本文的一些平衡策略起作用(如入簇半径),且节点剩余能量都较小,原因二是死亡节点通常是热区中路由消耗较小的节点,一旦它们死亡,路由消耗会成倍增加.本文取三个时间点的运行轮数都较高的概率为最优的候选簇头概率,本例的最优概率为0.11,其他规模网络所取概率见4.3节. 本文将网络死亡节点数达到30%视为网络失效[9].为观测UCOH算法在不同场景的性能,分别固定网络范围和固定节点数观测比较4种算法首节点死亡和30%节点死亡时网络运行轮数.图4为固定网络范围L=400,NS∈NA时4种算法对比,UCOH算法候选簇头概率随节点数目增大依次取0.12,0.11,0.11,0.1,0.09,Rcmp取45,45,45,40,40. 图4 网络范围固定时的网络寿命对比Fig.4 Comparation of network lifetime with fixed network range 从图4中可以看出随着节点数目的增大,各算法两个时间点的相应轮数基本上均有增加.当节点数较少时,节点信息交换能耗较少,SNNUC和UCDP算法竞选簇头时考虑的因素更周全,使得二者性能高于UCOH算法.当节点数目较多时,UCDP算法成簇协商能耗较大,节点数为2000时的运行轮数有所降低,性能差于SNNUC算法,而SNNUC与UCOH算法相比而言,UCOH算法的近基站节点能耗和成簇阶段信息交换能耗较少,并且多跳路径更优降低了路由能耗,故UCOH算法在两个时间点的运行轮数最高. 图5为固定节点数目NS=1600,L∈LA时运行轮数对比,UCOH算法候选簇头概率随网络规模增大依次取0.06,0.08,0.11,0.14,0.18,Rcmp取35,40,45,60,80.当网络范围增大时,节点距基站的平均距离更远,各算法两个时间点的运行轮数有降低趋势.规模较大时,密度较低,UCOH算法的热区评估准确性降低,但多跳跳数更优,性能相比之下有所下降,但不为最差.当规模较小时,UCDP算法即使在近基站成簇收益不能补偿成簇能耗的情况下也会频繁竞选区头和簇头,并且它与DEBUC算法的竞争半径未考虑节点密度,节点能耗均衡性不佳,造成两者运行轮数较低.UCOH算法热区量化较为精确,节点入簇更合理,加之采用相应策略防止了近基站能耗和信息交换能耗过大,故性能最好.综合图4图5及其分析说明UCOH算法更适用于密度较大的网络. 图5 节点数固定时的网络寿命对比Fig.5 Comparation of network lifetime with fixed number of nodes 图6为L=400,NS=2000和L=200,NS=1600时网络失效前的全局剩余能量曲线.可以看出密度较大时UCOH算法的能耗速率低于其他三种算法,例如在L=400,NS=2000的场景下,网络运行到450轮时,DEBUC、UCDP、SNNUC、UCOH网络剩余能量分别为:76.4J,98.2J,116.9J,159.8J,说明UCOH算法在平衡与节约能耗方面是有效的.而其中原因在于UCOH算法利用基站广播公共信息,限制近基站成簇,优化了跳数和中继节点,从而减缓了能耗速率.因此,与另外三种算法相比,UCOH算法更适用于密度较大的网络. 图6 全局剩余能量变化曲线Fig.6 Variation curve of the global residual energy of nodes 基于大密度的WSNs应用,本文在研究多跳网络最优跳数的基础上提出了一种非均匀时间竞争分簇算法,核心思想是:利用最优跳数指导簇规模的调整和下一跳路由的选取,缓解多跳路由中的“热区”和节省能量;通过限定成簇区域,减少近基站节点能耗;利用时间竞争簇头,节省节点信息交换的能耗;利用候选簇头中继,平衡节点负载.最终实验结果表明,对于密度较大的网络,本算法能有效节省网络能量,均衡能耗,延长特定生命周期特征的网络寿命. 本算法在仿真实验中有较好的性能,但还不适用于节点异构和节点可移动的网络,下一步将探索研究该类网络的路由算法.
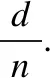
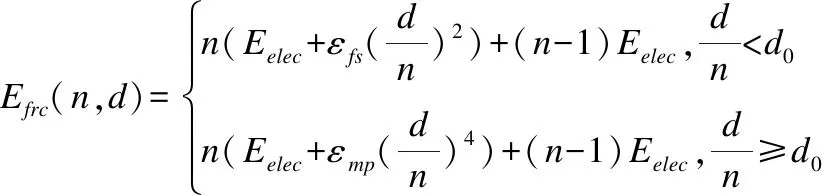
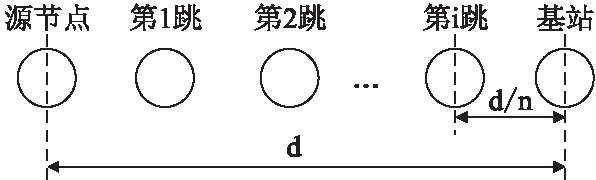
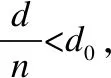
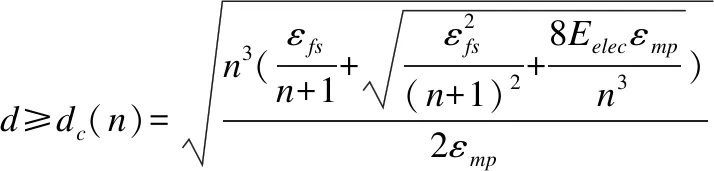
3 UCOH算法描述及分析
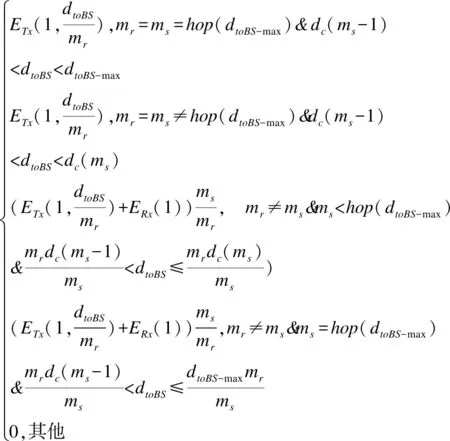
3.1 轮初始化
3.2 非均匀成簇
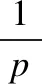
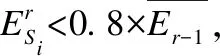
3.3 数据传输阶段

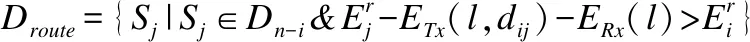

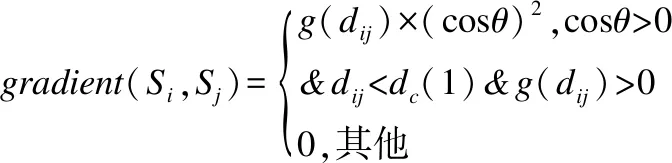

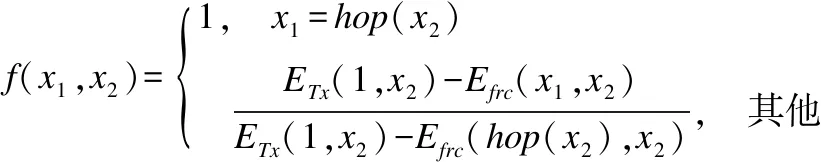
4 仿真与性能分析
4.1 仿真环境

4.2 候选簇头概率的确定

4.3 生存周期
4.4 能量效率
5 结束语
