分数阶微分方程非局部初值问题解的存在性*
2019-06-05彭云梦钟文勇
彭云梦,钟文勇
(吉首大学数学与统计学院,湖南 吉首 416000)
1 问题的提出
分数阶微分方程是指含有分数阶导数的方程,它起源于物理学、人口动力学和经济学等研究领域,是人们理解现实世界数学模型的重要工具[1].与经典分析类似,分数阶微分方程有分数阶常微分方程、分数阶偏微分方程、分数阶泛函微分方程和分数阶积分方程等.分数阶微积分和分数阶微分方程之所以能迅速发展,主要是因为它们不断扩展的广阔的应用前景[2].近年来,新定义下的分数阶微分问题成为国内外学者研究的一个热门问题.Ricardo Almeida等[3]研究了相对于另一个函数的Caputo型分数阶导数意义下局部初值问题解的唯一性和存在性;Gaston M N'Guérékata[4]研究了Riemann-Liouville分数阶导数意义下非局部初值问题解的唯一性和存在性;钟文勇等[5]研究了一类非线性分数阶微分方程非局部边值问题解的唯一性和存在性.对于非局部初值问题
(1)
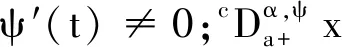
2 预备知识
文中假设阶数α为正数,用C=C[a,b]表示定义在[a,b]上的所有实值连续函数构成的Banach空间(该空间中的范数用‖·‖表示),Ck[a,b]表示[a,b]上具有直到k阶连续导数的实值函数全体.
定义1[6]定义于区间[a,b]的实值函数x相对于另一个函数ψ的α阶Riemann-Liouville分数阶积分
其中:函数ψ:[a,b]→R为递增函数;对于∀t≥a,都有ψ′(x)≠0.
定义2[3]定义于区间[a,b]的实值函数x相对于另一个函数ψ的α阶Riemann-Liouville分数阶导数
其中n=[α]+1,[α]表示α的整数部分.
定义3[3]设函数x∈Cn-1[a,b],则x的α阶ψ-Caputo分数阶导数
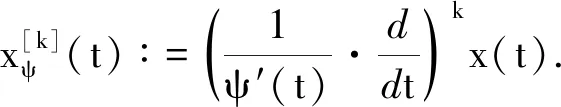

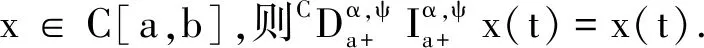
引理2[3]若函数x∈Cn-1[a,b],则

引理3[4](Krasnoselkii定理) 设M是Banach空间X中的一个非空闭凸子集.假设算子A,B满足以下条件:(ⅰ)对于∀x,y∈M,均有Ax+By∈M;(ⅱ)A是紧的且连续;(ⅲ)B是压缩映射.那么,存在z∈M,使得z=Az+Bz.
引理4[7](Banach不动点定理) 完备的度量空间中的压缩映照必然有唯一的不动点.
引理5[7](Arzela-Ascoli定理)C[a,b]中有界的等度连续函数族必是致密集.
3 主要结果及其证明
先作以下假设:
(H1)函数f:[a,b]×R→R是连续的二元函数;
(H2)f(t,x)关于第二变元满足Lipschitz条件,即存在正常数L,使得|f(t,x1)-f(t,x2)|≤L|x1-x2|,对于∀t∈[a,b],x1,x2∈R都成立;
(H4)对于∀(t,x)∈[a,b]×R,都有|f(t,x)|≤q(t),其中q∈C([a,b],R+).
首先证明分数阶Cauchy问题(1)与Volterra积分方程之间的等价关系.
定义4若函数x∈C[a,b]且满足问题(1),则称它为问题(1)的一个解.
定理1函数x∈C[a,b]是问题(1)的解,当且仅当x满足以下分数阶积分方程:
(2)

(3)
根据引理2可知,当α∈(0,1)时,
(4)
(3),(4)式联立,得到
利用初值条件x(a)+g(x)=xa,即得方程(2).
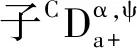
接着给出分数阶Cauchy问题(1)解的唯一性和存在性的充分条件.

证明定义算子F:C→C,
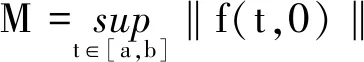
首先证明F定义是适当的,即F(Hr)⊆Hr,其中Hr∶={x∈C|‖x‖≤r}.对于x∈Hr,由假设(H2)和F的定义可知,
接下来证明F是压缩的.给定x1,x2∈Hr,由假设(H2)和(H3),有


定理3若假设(H1)—(H4)成立,则问题(1)在区间[a,b]上至少存在1个解.
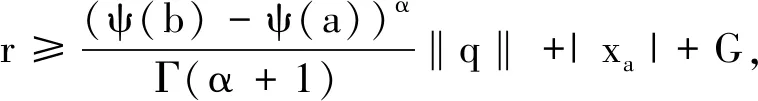
(Bx)(t)∶=xa-g(x).
由假设(H1)和(H4),可得不等式
即当x,y∈Hr时,Ax+By∈Hr.
接下来证明B是压缩映射.由B的定义可得‖(Bx)(t)‖≤|xa|+G≤r,因此B的定义是适当的,即B(Hr)⊆Hr.并且,当x,y∈Hr时,由假设(H3),有
|(Bx)(t)-(By)(t)|≤|g(x)-g(y)|≤p‖x-y‖,
即‖Bx-By‖≤p‖x-y‖,因此B是压缩映照.
最后,分3步证明A是紧映射.
(ⅰ)A是连续的.假设U中的xn是收敛于x的序列.由假设(H2)和A的定义,可得
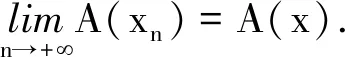
(ⅱ)将Hr中的有界集映射到有界集.给定x∈Hr,由A的定义和假设(H4),有
所以A是一致有界的.
(ⅲ)(Ax)(t)是等度连续的.因为连续函数f在紧集[a,b]×{x:|x|≤r,x∈R}上是有界的,所以定义d0∶=sup{|f(t,x)|:t∈[a,b],|x|≤r,x∈R}.假设t1,t2∈[a,b],t1 由中值定理和函数u(t)(u(t)=tα,0<α<1)在[a,b]上一致连续可知,(Ax)(t)是等度连续的. 由A是紧映射和Arzela-Ascoli定理可知,A是全连续的.由引理3可知,至少存在1个z∈Hr,满足z=Az+Bz,即问题(1)在区间[a,b]上至少存在1个解. 定理3去掉了对Lipschitz常数L的限制,给出了问题(1)至少存在1个解的充分条件.
