输油管道超声信号的小波包奇异值分解去噪

淦邦，彭云超，毛俊辉，李志向

（1.中国石化管道储运有限公司，江苏 徐州221008；2.北京理工大学，北京100081）

周知进等采用小波分析方法将超声回波信号进行分解［1］，适当设置门限阈值处理小波系数，然后对信号进行重构，有效地抑制了信号中噪声对测量精度的影响。罗雄彪等对超声检测的缺陷回波信号进行了小波包分析［2］，其结果表明，利用小波包阈值去噪，大幅提高了缺陷回波信号的信噪比，改善了信号特征信息的质量，并且具有较高的缺陷定位精度和纵向分辨率。卢超等采用一个尺度间变化的门限阈值来抑制噪声的小波变换系数，并以各尺度缺陷信号的能量关系形成权值，加权重构信号来提高信噪比。然而小波分解只能对信号的低频信息进行分解，不能利用高频信息，小波包分析尽管可以同时利用高频和低频信息，但小波阈值滤波常用软阈值和硬阈值两种方法，硬阈值方法能很好地保留信号的特征，但会使滤波后信号产生附加振荡，不具有良好的光滑性；软阈值方法尽管能够使信号具有像原始信号一样的平滑性，但往往造成信号失真［3-4］。

综上所述，本文提出一种小波包奇异值分解去噪方法，通过某小波基函数，对回波信号进行小波包分解，依据不同频带能量分布比，提取能量分布集中频带，利用奇异值分解方法确定有效回波信号区域，从而实现自适应滤波。

1 小波包分析理论

小波分析的基本思想是用一簇函数去表示或逼近某一信号，该簇函数叫小波函数系，它是一种多分辨率分析方法，该方法不仅可以提取信号在不同频带上的特征，而且可以保留信号的时域特征，但小波分析只对信号的低频部分进行分解，却不分解高频部分，其高频分辨率很差。而小波包分析能同时分解信号的低频和高频部分，克服了小波分析的缺点，具有很好的时频分辨率。

根据小波多分辨率分析理论，小波函数和尺度函数存在两尺度关系［5］：

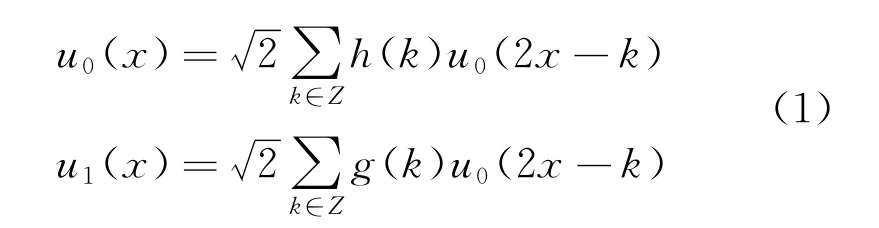
式中：h（k），g（k）——小波函数确定的滤波器；u0（x）——尺度函数；u1（）——小波函数。由式（1）可得：

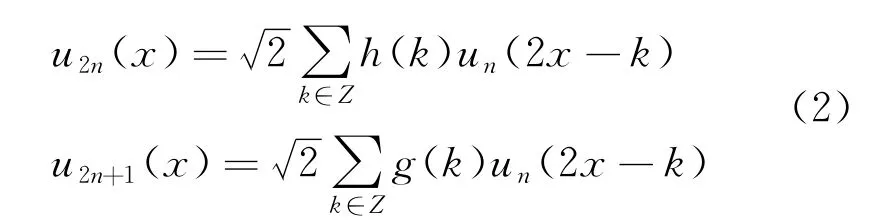
式中：n——分解尺度为j时的第n个小波序列。

式（2）确定的序列称为由正交尺度函数确定的小波包。若定义为函数）的闭包空间，而是函数的闭包空间，将小波子空间和闭包空间统一起来，可将分解为

从图1以上数据可以看出，与全球系统重要性银行相比，当前四大行的资本充足率均低于G-SIBs平均资本充足率(16.32%)，四大行面临资本金的制约。资本充足率指标决定了商业银行必须转变发展方式，由原来的“信贷依赖症”、“粗放发展症”，向内涵式集约化追求质量和效益的方式转变。国际上大银行，通过较高的盈利能力留存补充资本，促进贷款投放，形成了资本的良性循环机制。虽然通过发行普通股等方式可以补充资本金，一定程度上缓解资本的压力，但仅仅依靠融资方式补充资本既受制于监管政策，又取决于资本市场的容量，因此，以RAROC为核心，通过改善资产结构、提升资本使用效率是解决问题的根本途径。

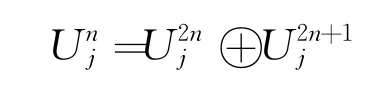
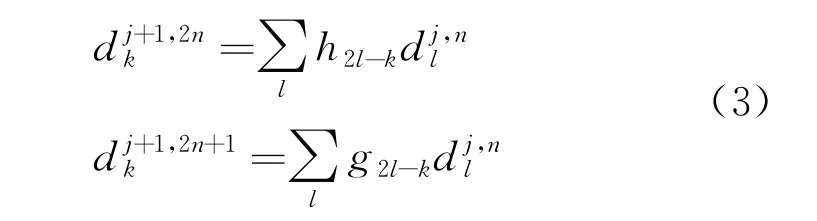
式中：l，k——与尺度函数紧支集相关的参数。

由式（3）可知，小波包系数分解每次都是两个序列，对应分解信号的低频部分和高频部分。分析分解后的信号，找到有用信号的特征，再对这些信号进行小波包重构，可有效去除信号中不必要的成分。小波包信号重构算法：

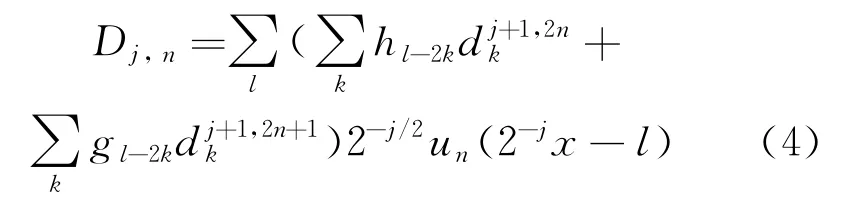
2 奇异值分解理论

设A为m×n维矩阵，矩阵的秩为r，对矩阵A进行奇异值分解，可得［6-7］：

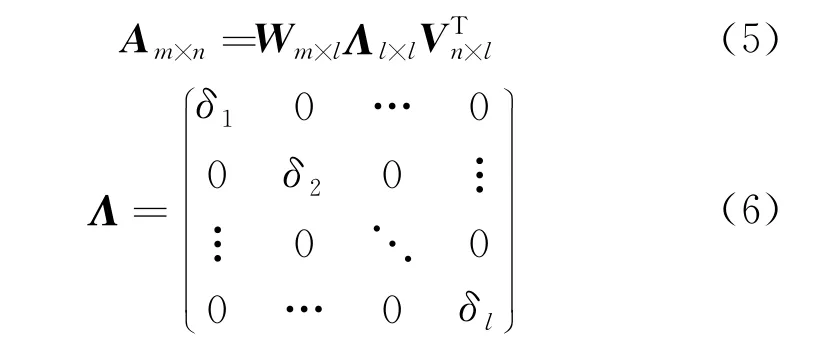
式中：Λ——l×l的对角阵。

式（6）中对角元素满足δ1≥δ2≥…≥δl≥0，矩阵Λ所有的对角元素称为矩阵A的奇异值，对某一含噪信号进行奇异值分解，若求得奇异值中零的个数越多，表明该信号的信噪比越好。

3 小波包奇异值分解算法

设原始信号的离散时间序列为f（t j），噪声的离散时间序列为σ（t j），则检测到的实际离散时间序列用式（7）的数学模型表示：

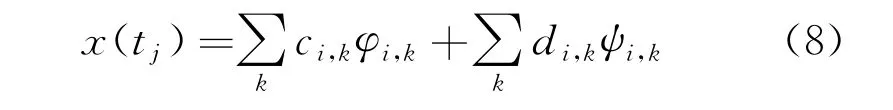
信号经过i层小波包分解，可得2i个小波包，每个小波包对应离散时间序列x（t j）中的某段频率成分。小波包分析对信号低频和高频都具有很强的分析能力，小波包分解后的系数不仅有有用信号的高频信息和低频信息，同时也有噪声信号的高频信息和低频信息，但有用信号往往集中在某一频段范围内，若采用小波包软硬阈值去噪，会产生上述的问题，若采用改进的阈值消噪法，在信噪比较低时，阈值的选择会随着噪声的增加而增大，极易将部分有用信息去除造成信号的失真［8］。由能量守恒定律，利用式（9）可求得小波包分解后各频段能量：

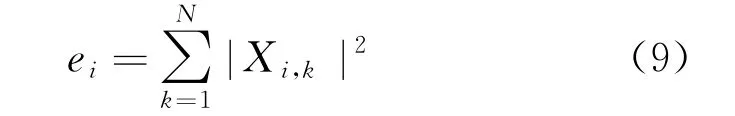
式中：X i，k——离散点幅值。

通过对小波包分解后各频段能量的分析，可确定有用信号主要集中在哪些频段，提取这些频段并进行重构，能有效地去除部分噪声信号。对提取的小波包系数重构后进行奇异值分解，分解后的奇异值集中体现了有用信号和噪声，较大的奇异值主要反映有用信号，其余的奇异值反映噪声，对分解后的奇异值进行奇异熵分析确定最佳阶数，可得到良好的去噪效果。小波包奇异值分解算法步骤如下：

1）对输油管道超声信号进行小波包分解，首先选用最优小波基函数，设定分解层数，小波包系数分解原理如图1所示。由图1可知，对超声信号进行3层小波包分解后，得到的8个节点，8个节点同时分别对应某段频率范围。

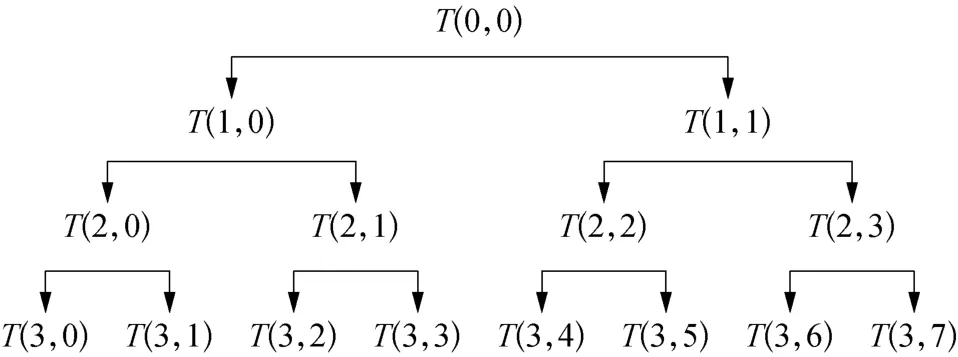
图1 小波包系数分解原理示意

2）提取8个节点的小波包系数，对8个节点小波包系数进行重构，得到8个节点对应的信号，依据帕斯瓦尔定律，计算每个节点信号的能量，并利用每个节点信号能量与信号总能量的百分比构造的能量特征向量来表示有用信号与噪声信号的能量关系。

3）根据能量关系，对提取的某些频段（节点）的信号进行重构，剔除高频干扰信号；对提取的重构信号进行奇异值分解，用式（9）计算信号的奇异熵［10］：

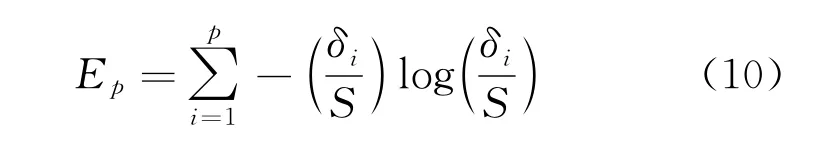
4）将信号奇异熵的饱和阶数作为阈值进行超声信号消噪，最佳阶数的选择依据文献［9］进行分析。根据得到的最佳阶数，将奇异值中较大的保留，较小的奇异值点用零代替，得到新的奇异谱，利用算法重构新的数据矩阵，得到去噪后的输油管道超声信号。小波包奇异值分解算法流程如图2所示。

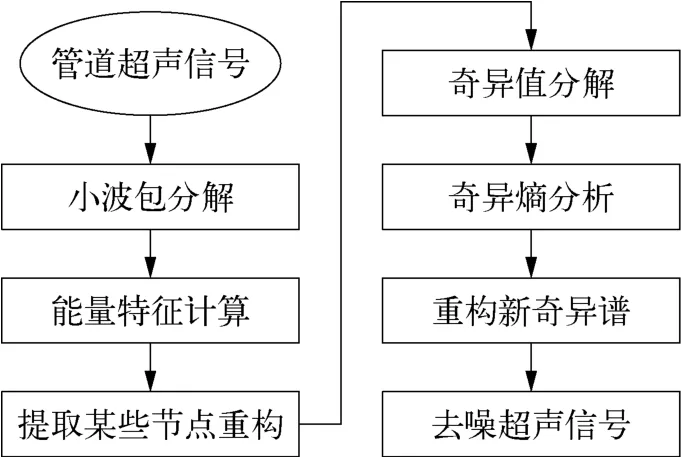
图2 小波包奇异值分解算法流程示意

4 结果分析

为验证小波包奇异值分解算法的去噪有效性，对一块阶梯钢试块进行了实际的超声检测试验。试验所用阶梯钢试块的材料与实际管道相同，由4个台阶构成，各台阶的高度分别为10，8，7，6 mm。试验检测系统由水浸聚焦超声探头、脉冲式超声收发卡、四通道泰克数字存储示波器、工控机等组成。

试验中选择采样频率为25 MHz。阶梯钢试块某一台阶检测回波信号时域波形如图3所示，回波信号含有大量的噪声信号，该情况对于信号的判断和自动扫查时门槛阈值的设定造成了一定的困难，严重影响检测的灵敏度和分辨力。

采用小波包奇异值分解算法对回波信号进行去噪后的波形如图4所示，去噪时选择sym8小波基函数对回波信号进行小波包分解，分解层数为3层，对每一个节点进行小波包重构，计算每个节点能量与总能量的百分比，得到各个节点能量分布特征。根据各节点能量分布特征对节点信号进行重构，重构后的信号进行奇异值分解，确定最佳奇异熵饱和阶数为4，将奇异熵饱和阶数作为阈值得到新的奇异谱，利用新的奇异谱重构超声回波信号。

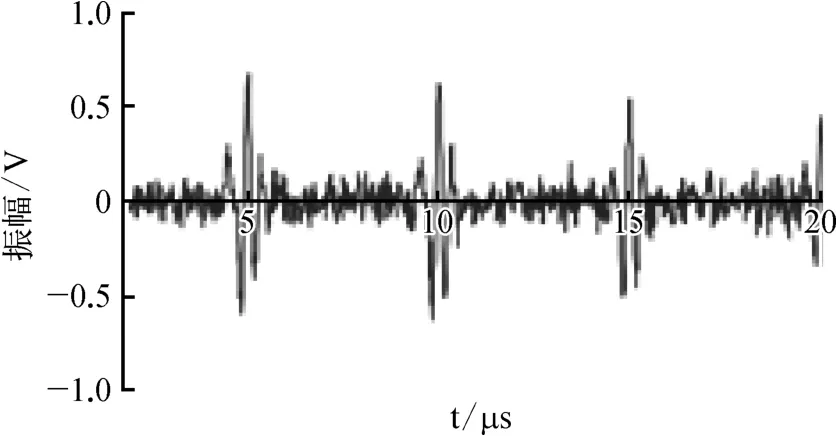
图3 阶梯钢试块缺陷超声回波信号时域波形示意

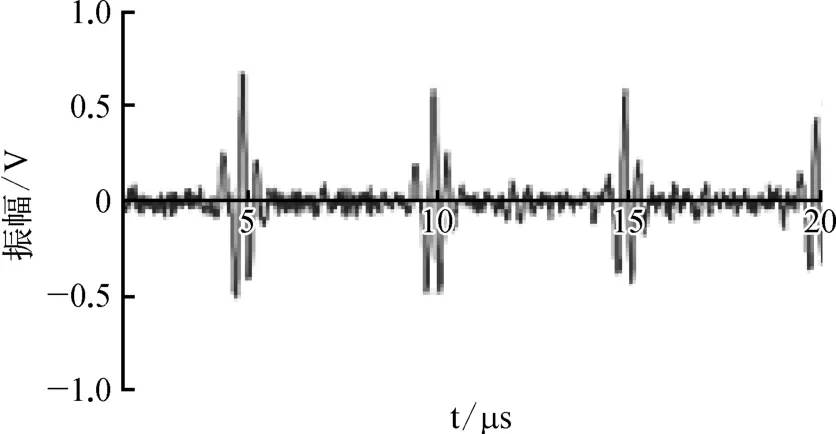
图4 小波包奇异值分解去噪后的波形示意

比较图3和图4可发现，采用小波包奇异值分解算法大幅减少了噪声干扰，可清晰地看到回波信号，为检测时门限阈值的设置和缺陷的定性定量分析奠定了良好的基础。

5 结束语

根据小波包阈值去噪的不足，针对超声回波信号的特点，利用奇异值分解对原始信号中的噪声具有良好敏感性的优点，提出了一种小波包奇异值分解去噪算法模型。实验结果表明，采用小波包奇异值分解去噪算法不仅能去除高频噪声，同时也能有效减少低频噪声，大幅提高了信号的信噪比，非常适合于管道超声扫查信号的分析和去噪，为防止出现管道缺陷的漏判、误判打下了良好的基础，具有良好的工程应用价值。