大气折光系数测定及在悬索桥基准索股线形测量中的应用
2019-06-05刘成龙杨雪峰
王 欢,刘成龙,杨雪峰,王 永
(1. 西南交通大学地球科学与环境工程学院,四川 成都 611756; 2. 高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都 611756; 3. 广东省长大公路工程有限公司,广东 广州 511431)
虎门二桥主线全长12.891 km,该桥起点位于广州市南沙,终点位于东莞市沙田。其主桥由坭州水道桥和大沙水道桥两座超大跨度悬索桥构成,其中坭州水道桥采用548+1688 m双跨钢箱梁悬索桥,跨越坭洲水道桥位处河面宽度约2300 m,是整个虎门二桥的控制性工程。在悬索桥施工过程中,主缆架设[1]是一项重要的施工内容。主缆线形能否精确调整到设计位置,直接关系到成桥的线形和受力状态。因此,在主缆的架设过程中,要综合考虑各种因素,对主缆的线形进行控制,保证主缆架设的精确性。基准索股[2]作为主缆的第一根索股,为一般索股架设提供基准,其中跨和两个边跨垂度的精度直接影响着主缆的线形,是整个主缆线形控制的重中之重。
由于大跨度悬索桥基准索股跨中位置处于百米高空,因此其高程(又称绝对垂度,简称垂度)测量只能采用三角高程测量法进行测量;又因为基准索股上无法架设全站仪,所以垂度只能进行单向三角高程测量[3-4]。众所周知,大气垂直折光和地球曲率对单向三角高程测量精度的影响尤其显著[5],除此之外量测仪器高和棱镜高的误差也是主要误差源。为提高基准索股和主缆线形架设的精度,保证悬索桥上部构造工程质量,本文提出利用桥址区实时大气垂直折光系数改正的单向三角高程测量法,进行悬索桥基准索股的跨中垂度测量。
1 两岸高差基准的精确建立
为保证桥址区大气垂直折光系数的准确测定,首先需要进行两岸高程控制点间高精度高差的测量。特大型悬索桥高程控制网按照设计要求,应达到二等高程测量及以上精度的要求。目前,两岸水准点间及待测大气折光系数(K值)边的高差测量,通常采用两台高精度智能型全站仪进行同时对向间接高差三角高程测量[6]的方法。原理如下。
要实现两岸水准点间的二等跨河三角高程测量,需要布设如图1所示的跨河测量场地。在图1中,A、B、C、D为4个跨河高程测量的临时水准点,同岸两个跨河临时水准点间相距20~30 m左右,并且均采用二等水准测量方法测量其高差。两岸全站仪分别架设在距跨河点15~20 m左右的位置,这样两台全站仪即可实现对4个临时水准点上方的棱镜进行同时对向测量。跨河测量时,在这4个临时水准点上用脚架和基座摆放三棱镜(由于跨河距离在2 km以上),两台智能型全站仪自由测站整平后同时对4个三棱镜进行斜距和垂直角测量。由于全站仪安置时是自由测站,所以不需要量测仪器高,因此该方法没有仪器高量测误差。
4个临时跨河水准点与其上方架设的棱镜间的高差(即棱镜高)测量,利用全站仪加定长棱镜装置,采用中间法三角高程法[7]来测量,其原理如图2所示。这种方法量测棱镜高,误差能够控制在0.3 mm以下。
跨河测量时,两台全站仪均对4个跨河点棱镜同时进行多测回斜距和垂直角的自动观测。外业观测的时段数、测回数和斜据、垂直角观测技术要求,按照相关规范要求执行。
对外业观测数据进行处理,即可计算得到图1中AC、AD、BC、BD4段间接高差。同一段各双测回的间接高差应进行互差检验,其互差应满足限差要求[8]。由大地四边形组成3个独立闭合环,用同一时段的各条边高差计算高差闭合差,各环线的高差闭合差应不大于规定的限差要求。当外业观测数据满足各测回间高差互差限差和各环线高差闭合差的限差要求后,计算4个跨河测段的高差均值。利用实测4个跨河测段的高差均值和岸上AB、CD测段水准往返测高差的均值,可以计算图1中5个闭合路线的高差闭合差。表1为虎门二桥按照上述方法进行跨河高差测量后的跨河大地四边形高差闭合差计算结果,从表1中的实测闭合差及其闭合差限差可以看出,本次跨河测段高差和岸上测段高差测量的高差闭合差全部满足其限差要求,因此可以说明本次跨河高程测量的高差数据满足二等高程控制测量的精度要求。
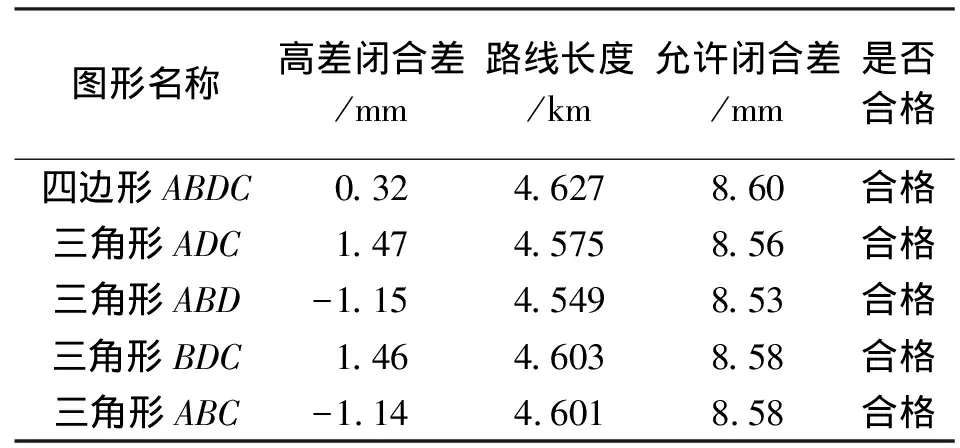
表1 跨河测段高差闭合差统计
注:表中的允许闭合差限差按照二等水准的限差要求计算。
2 桥址区大气垂直折光系数测定及改正试验
2.1 折光系数测量原理及数据处理
以AD边为例,针对AD边大气垂直折光系数的测定,需在A点架设全站仪,在D点安装棱镜,如图1所示,并精确量取仪器高和棱镜高。之后,每个小时对AD间的单向三角高差进行两测回观测,连续测量24 h,并记录实时温度。利用外业不同时段测量的观测值,可以计算得到每个时段AD间的单向高差,并采用上面跨河测量方法得到的该边的精确高差和式(1),即可计算得到该边不同时段的大气垂直折光系数K。
(1)
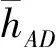
按照上述方法测量得到的虎门二桥AD边24 h的折光系数见表2。分析表2中的折光系数可以得出如下规律:①同一条边不同时段的K值变化较大,即折光系数随时间变化;②晚上11点至第二天凌晨5点,气象条件相对比较稳定,K值也相对稳定。
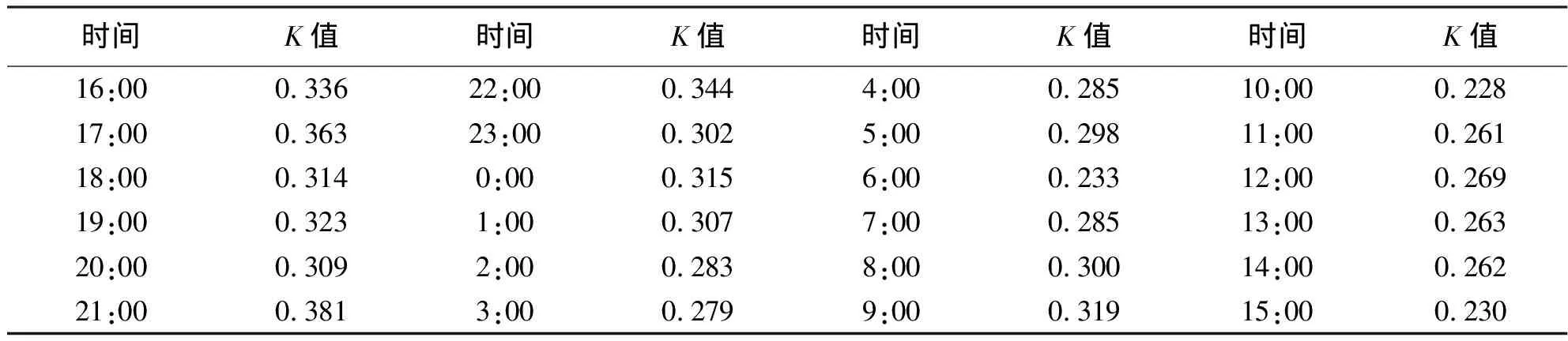
表2 AD边24 h大气折光系数统计
2.2 单向三角高差实测改正试验
所谓的单向三角高差实测改正试验,就是用实测的大气折光系数,对单向测量的三角高差进行改正,并用改正后高差和该边已知二等高差进行对比,来验证桥址区所测K值对实测单向三角高差的改正效果。
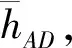
(2)
式中,R为地球曲率半径;S0为A到D实测平距;K为按照上述方法测量的大气垂直折光系数。
在虎门二桥进行的实测单向三角高差大气垂直折光系数改正试验中,对4条跨河边(4条跨河边中有长短边,短边与边跨垂度单向三角高程测量的距离大致相同,长边与中跨垂度单向三角高程测量的距离大致相同)的实测单向三角高差利用对应时间段的折光系数进行改正计算试验。这4条跨河边改正前、后高差和已知二等高差的对比情况,见表3。
通过分析表3中的数据,可以得出以下结论:①球气差(地球曲率和大气折光)对单向三角高差的影响显著,改正前对短边的影响达到20 mm以上,对长边的影响达到了325 mm以上;②对各边实测单向三角高差进行大气垂直折光系数改正后,与精密二等高差的差值较小,最大差值不足5 mm,说明改正后的高差达到了较高精度,可为后续实际应用提供参考。
以上试验结果表明,采用单向三角高差的实时折光系数改正方法,进行特大型悬索桥基准索股垂度测量与调整是切实可行的。

表3 K值改正前、后高差与二等高差对比情况统计
3 在悬索桥基准索股线形测量与控制中的应用
3.1 基准索股垂度测量与调整
悬索桥基准索股线形的测量与调整,就是对基准索股主跨和边跨的跨中点进行垂度测量与调整,从而使基准索股几何线形达到设计线形,即自由悬挂时为悬链线形的状态[9]。在基准索股垂度测量时,利用单向三角高程测量法,并对单向高差进行实时大气折光和地球曲率改正,最终得到跨中点的实测高程。同时,在当前工况下,根据基准索股控制线形[10-11]计算公式,可以计算跨中点的设计高程。在同一工况下,根据实测高程与设计高程之间的偏差值,就可以对跨中点进行垂度调整。
本文以虎门二桥中跨基准索股垂度测量与调整为例,介绍采用本文方法进行基准索股垂度测量的方法及其效果。该桥中跨基准索股垂度采用东、西两岸两测站同时进行测量的方法进行对比分析,以提高中跨基准索股垂度测量的可靠性。此时测站与测点间的关系大致是:测站与测点间的距离大约为1200 m左右,跨中点的高度约为98 m左右,从测站到基准索股跨中测点的垂直角约为4°32′。实际跨中垂度测量时,全站仪采用强制对中,仪器高量测误差小于0.5 mm;棱镜采用特制装置(该装置设置上下对称的双棱镜,双棱镜高程取均值后刚好是基准索股中心),可以不量测棱镜高,因此没有棱镜高的量测问题。
3.2 基准索股中跨垂度测量精度估算
根据特大型悬索桥的设计要求,基准索股中跨的垂度允许误差为(-10 mm,20 mm),中跨上、下游两根基准索股垂度间的相对垂度误差不得超过10 mm。
利用单向三角高程测量法进行跨中点垂度测量,计算测站点A到跨中点B的高差公式为
h=Ssinα+i+f
(3)
式中,S为斜距;α为垂直角;i为仪器高;f为地球曲率和大气折光改正。
将式(3)全微分并转化为中误差关系式[12],便可以得到单向三角高程测量高差中误差的估算式
(4)
式中,mS为测距中误差;mα为竖直角测角中误差;mi为仪器高量取中误差;mf为球气差改正中误差。
进行中跨跨中点垂度测量时,采用测距标称精度为0.6 mm+1×10-6D和方向测量标称精度为0.5″的全站仪,则mS=±1.3 mm、mα=±0.5″;仪器高在强制观测墩上使用钢板尺测量,mi=±0.3 mm。依据文献[13]及该桥测定跨中点折光系数的现场条件,计算得到K值中误差mK=±0.07,进而得到mf=±7.9 mm。把以上各值代入式(4),则计算得到mh=±8.4 mm。

3.3 主跨跨中点垂度测量结果与分析
根据上文可知,基准索股主跨跨中点采用双测站进行垂度测量,并且采用实时的大气折光系数进行单向三角高差改正。当两测站所测同一跨中点绝对垂度互差小于10 mm,则取双测站所测垂度均值作为该跨中点的垂度值。该桥主跨上、下游两根基准索股垂度测量和调整进行了5轮测量;在基准索股垂度达到要求后,再进行3天的基准索股垂度稳定性监测,每天的基准索股垂度稳定性监测进行4轮测量。由于篇幅所限,下文仅给出主跨上游侧基准索股调索和稳定性监测时的中跨垂度测量结果及上、下游两基准索股间的相对垂度偏差,结果见表4、表5。
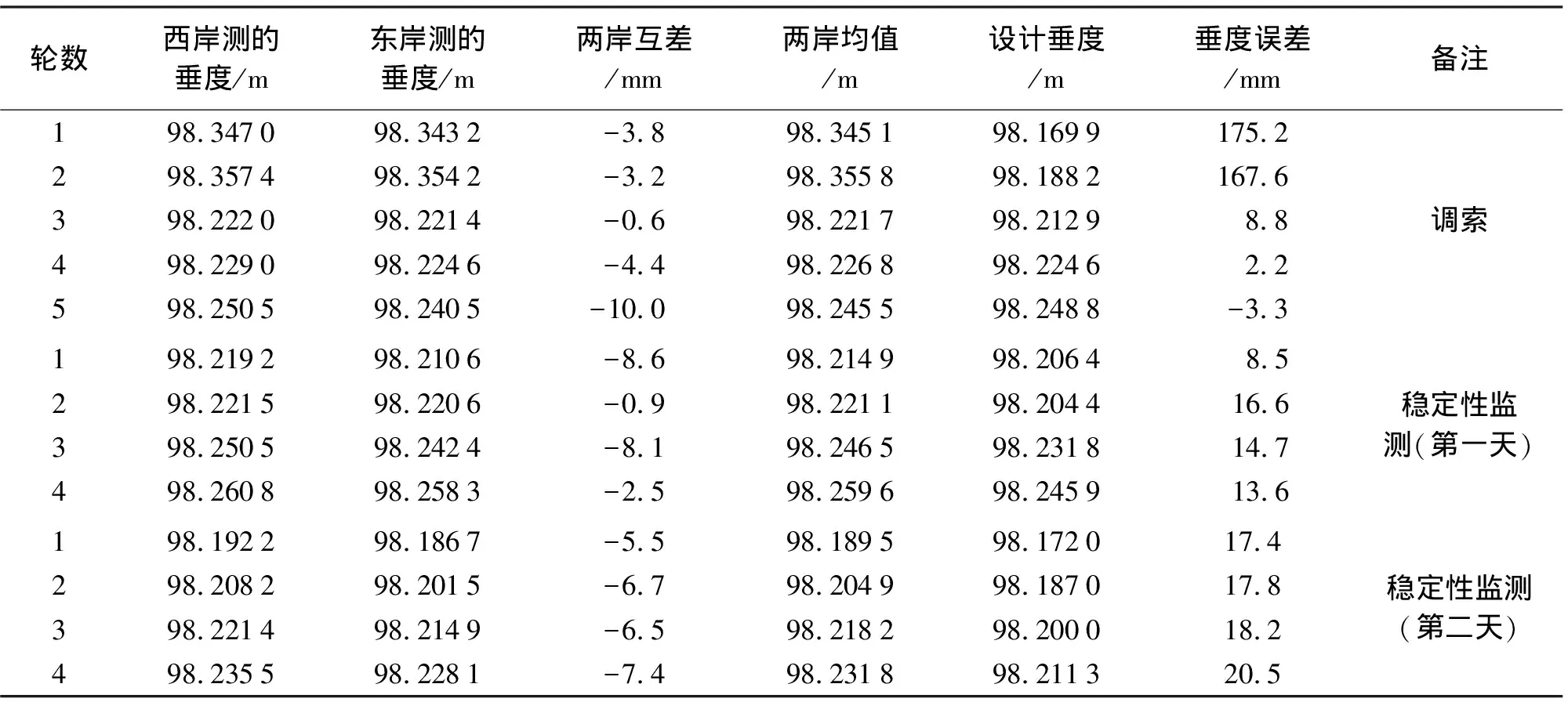
表4 上游侧基准索股中跨跨中垂度测量结果

续表4
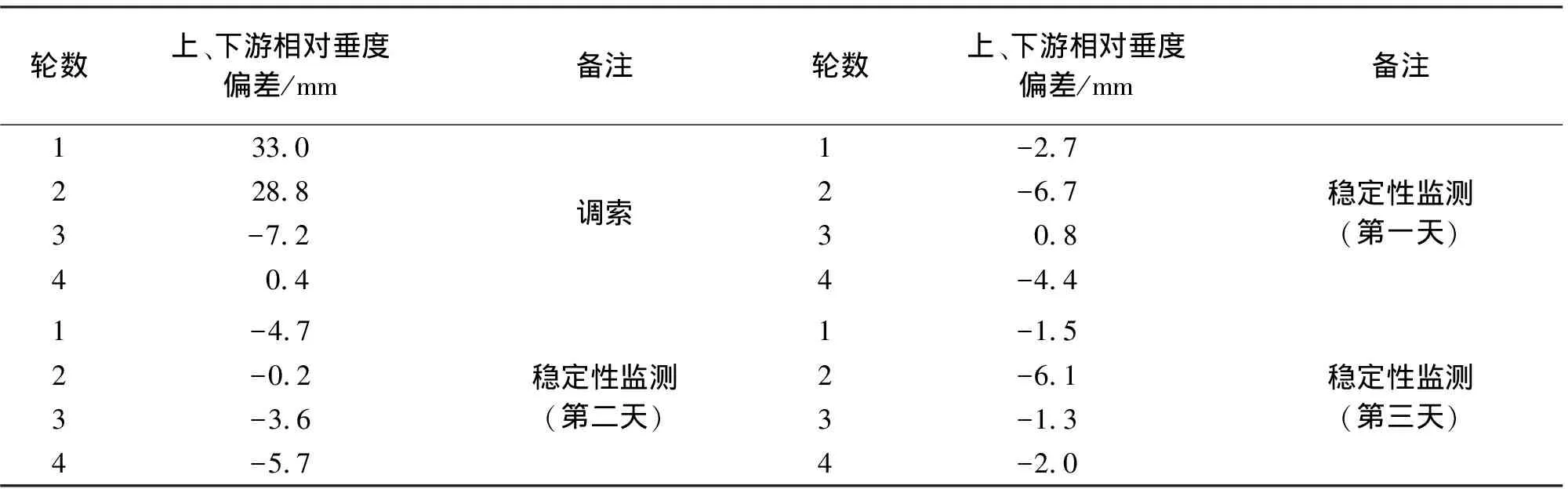
表5 主跨上下游基准索股相对垂度偏差统计
由表4和表5可以看出:
(1) 在东、西岸对主跨跨中基准索股垂度进行两测站测量,单程测量距离均超过1 km。通过利用实时的折光系数进行单向三角高差改正,使得两岸所测中跨跨中的垂度值互差均小于10 mm,达到精度要求,保证了主跨跨中点垂度测量结果的精度和可靠性。
(2) 3天的稳定性监测结果可以得出,实测基准索股中跨跨中垂度与控制线形计算垂度的差值均满足基准索股架设精度要求,也就是说该基准索股绝对垂度均满足设计精度要求。
(3) 该桥主跨上、下游两基准索股间的相对垂度偏差,也满足10 mm的设计精度要求。
4 结 论
综上所述,虎门二桥基准索股垂度测量结果达到设计精度要求,且稳定性较好。说明本文提出的基于大气折光系数实时改正的单向三角高程基准索股垂度测量方法是正确并且可行的,完全能够解决不能采用精密水准和对向三角测量进行特大型悬索桥基准索股定位的技术难题,对于其他悬索桥的基准索股垂度测量与调整有借鉴意义。
