基于衰减记忆思想的故障容错方法

高 超，赵修斌，庞春雷，王 勇，张 闯

(空军工程大学信息与导航学院，陕西 西安 710077)

目前，基于SINS+GNSS的组合导航技术已经十分成熟，在航空航天、水面舰艇、弹箭制导和大地测绘等领域得到了广泛应用[1-2]。但在工作中，可能会受到多路径现象或欺骗式干扰等情况的影响，需要及时进行故障诊断。

常用的故障诊断方法有χ2检测法和改进的SPRT方法。其中状态χ2法[3]和改进的SPRT方法[4]常用于缓变故障的检测。状态χ2法通过比较卡尔曼滤波器与状态递推器状态量的差异，判断滤波器中状态量是否被故障信息污染，但递推器会存在因无量测更新而导致误差积累的问题。对此文献[5]最早提出使用双状态χ2法，用两个递推器交替作为故障参考系统，能够较好地解决该问题，但确定递推器交替工作的时间没有合理的方法，大多使用经验值[6]，且递推器受初始值的影响远大于滤波器[5]，而在实际应用中准确的初始信息较难获取。改进的SPRT方法通过迭代递推检测缓变故障，存在一定检测延时，且其对故障结束时间不敏感。文献[7]通过残差χ2法的辅助判断故障结束，并对改进的SPRT检测函数值置0使其用于后续检测，但当故障结束时，若故障幅值小于残差χ2法能够检测到的门限，会出现漏检，使该方法失效。针对突变故障，残差χ2法利用数据突变的特点，通过残差构造检测函数，对幅值较大的突变故障检测效果明显。残差χ2法作为系统级故障检测法，在检测到故障后，通常弃用故障传感器信息，在SINS+GNSS松组合导航中，弃用故障量测信息，改用一步预测值进行更新，但这会造成有用信息的浪费和精度上的降低[8]。

本文充分研究残差χ2法的检测特性，给出故障能被检测到的最小幅值，当突变故障幅值小于该值时，提出一种基于衰减记忆思想的故障容错方法，用改进SPRT方法检测故障，利用衰减因数减小包含故障信息的陈旧滤波值的权重，同时构造“伪正常”状态，使该方法能够及时判断故障结束。通过仿真，验证了该方法的有效性。

1 故障量大小的区分

将系统状态量和量测量表示如下

Xk=Φk,k-1Xk-1+Γk-1Wk-1+νδ(k-1,γ)

(1)

Zk=HkXk+Vk

(2)

式中，Φk,k-1为系统状态转移矩阵；Wk为系统噪声向量；Γk-1为系统噪声矩阵；Vk为观测噪声向量；Hk为量测矩阵；ν表示故障量幅值；δ(k-1,γ)为Kronecker函数，当k-1=γ时，取1，否则取0。Wk与Vk为互不相关且为零均值白噪声序列。

残差χ2法在一定的误检率和漏检率下进行故障判别，为了更好地研究残差χ2法的检测效果，下面分析故障幅值大小的影响。

假设故障发生在某一维观测量上，故障信号幅值表示为ν，该维残差向量表示为

(3)

相应的残差均值由0变为v，由故障引起的统计量的变化为

(4)

式中，Pδi表示残差方差阵对角线上第i个元素。可以看出故障幅值越大，检验统计量也就越大，就越容易被检测到。

根据文献[9]，在一定的误检率和漏检率下，可以计算出非中心化参数λ0，则最小可检测误差(minimal detectable biases,MDB)表示为

(5)

当故障发生在多维观测量时，统计量为

(6)

MDB表达式中的分母为m个残差协方差阵对角线元素的和。根据以上分析，当故障量小于或等于最小可检测误差时难以被检测到，可以认为是小幅值故障。

2 改进的SPRT方法

当状态量为正态分布时，改进的SPRT检测方法按照以下过程计算检测函数。

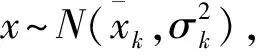
(7)

(8)

则观测序列必将从两个假设中作出判断。

根据两者概率密度可以得到对数似然比[10]

(9)

对数似然比的递推计算公式为

(10)

改进的SPRT方法只需一个检验阈值，其计算方法为

(11)

式中，Pf为误检概率；Pm为漏检概率。

故障判决准则为

3 结合衰减记忆思想的故障容错方法

衰减记忆滤波原是针对模型误差和噪声统计特性不准引起的滤波发散问题，由于滤波过程中误差方差阵和增益的计算与模型误差无关，造成滤波增益逐渐减小[11]，导致最新的量测值对状态估计的修正作用减小，最终可能引起滤波发散。衰减记忆滤波通过增大最新量测值的权重来抑制可能出现的发散问题，即在计算一步预测协方差时，多了一个标量因子S，这里S>1，相比原方程，增益矩阵变大，这意味着新的量测的权重会增大。

衰减记忆滤波方程为[12]

(12)

基于此，在SINS+GNSS松组合无冗余观测信息情况下，本文将衰减记忆思想引入故障容错策略中，提出一种新的故障诊断方法：

(1) 利用改进的SPRT方法对滤波残差进行检测，针对导航位置和速度，计算6个分量的故障检测值，当有任一检测函数值超出门限，判断该维分量出现故障，否则认为无故障。

(2) 确定故障分量后，首先对该维分量的残差置0，构造“伪正常”状态，使改进的SPRT方法在后续检测时能够敏感数据大小，可以及时判断故障结束；后对卡尔曼滤波方程作重构处理，用无故障的量测数据，建立新的降维量测更新方程进行滤波。

(3) 根据衰减记忆思想，利用衰减因数，减小故障发生后因未被检测到并隔离的错误数据影响,加大隔离故障后的正确数据在滤波过程中的权重，以此提高滤波精度。

(4) 重复上述检测和滤波步骤。

4 仿真试验

为验证本文提出的基于衰减记忆思想的故障容错方法的有效性，在SINS+GNSS松组合导航方式下，设计卫星数据出现故障时的仿真试验。

设定无人机飞行轨迹，考虑飞机可能存在的飞行状态，包括起飞、转弯、平飞和降落。飞机初始位置设为(34°N，108°E)，高度0，初始速度为0，初始方向为正东。仿真中设置惯性器件的误差分别为陀螺随机常值漂移为0.1 (°)/h， 加速度计随机常值漂移为10 μg；卫星数据的误差分别为位置误差10 m，速度误差0.1 m/s，仿真时长为25 min。

4.1 故障大小的分析

SINS+GNSS松组合导航中观测量包括三维位置和三维速度，首先分别得到每个观测量的最小可检测误差(MDB)，如图1所示。本文设定检测方法的误检率和漏检率均为0.005，则残差χ2法检测门限为18.548，改进SPRT方法的检测门限为5.293，对应的非中心化参数λ0为17.872。

由图1可知，残差χ2法对位置观测量的最小可检测误差约为42.5 m，对速度观测量的最小可检测误差约为0.42 m/s。据此仿真观测量出现故障的情况，人为添加故障见表1，结果如图2所示。

/s/m1300～480302300～480403300～480604300～48080

从纬度故障可检测程度来看，故障幅值在小于或等于40 m时，MDB值与无故障情况相差不大，因此难以检测，当故障幅值在MDB两倍以上时可以很好地被检测到。故障检验统计量表明：故障模式1下，纬度故障值30 m小于最小可检测误差，残差χ2检测法基本无效；故障模式2下，纬度故障值40 m与最小可检测误差非常接近，利用残差χ2法检测时，当故障初次出现时，检验统计量没有大的突变，故障持续期间；故障模式3下，纬度故障值60 m，在故障初次出现时，能够体现出残差χ2法对突变故障的敏感性，但仍会发生漏检；故障模式4下，残差χ2法能准确检测，检测效果较好。

考虑只有一维观测量有故障的情况，故障在小于或处于最小可检测值附近时，属于检测盲区，难以被准确检测。通过仿真分析，当故障量为最小可检测值的两倍以上时，可以被很好地检测，其余各观测量所得结果一致。至此可以作为故障幅值大小的区分准则。

4.2 故障容错方法性能分析

由上述分析可知，当出现小幅值突变故障时，残差χ2法不能正确检测并隔离故障，针对该问题，使用本文提出的故障容错算法，故障情况设置为表中模式1，结果如图3所示。

(1) 图3(a)表明，普通改进SPRT方法与本文故障容错方法在检测小故障时有相同延时41 s，但后者利用“伪正常”状态能准确判断故障结束时间，因此可用于故障多发情况。

(2) 图3(b)纬度误差均方差分别是残差χ2法为7.596 m，改进SPRT方法为5.503 m，本文算法为1.968 m。其中残差χ2法不能正确检测到故障，故障数据会引起滤波发散并降低导航精度，改进SPRT方法在故障结束后缺少有效量测信息，滤波输出值恢复到正常水平用时较长。本文算法利用衰减记忆的思想，减小了检测延时期间数据权重，且最快利用了故障结束后的正确量测信息，提高了滤波精度。

4.3 故障多发情况的检测分析

考虑改进的SPRT方法对故障结束会有检测延时，在验证故障多发情况下的检测时，依据上述检测结果，分别在误检延时期间和延时外添加相同故障，设置故障模式见表2，结果如图4所示。

结果表明，当二次故障发生在改进SPRT方法的误检延时内，检测函数会持续告警，且故障数据越多，误检延时越长，相应的滤波精度越低；当二次故障发生在改进SPRT方法的误检延时外，相当于独立发生两次故障，对于后续检测区别不大。本文提出的方法，通过“伪正常”状态的构造，能够及时检测故障结束，可以更长时间地利用可靠数据进行滤波。出于对故障发生时间间隔未知性的考虑，及时判断故障结束，能够在故障多发的情况下，提供更高精度的导航结果，对于增强系统可靠性具有重要意义。

表2 故障多发设定情况

5 结 语

本文针对SINS+GNSS组合导航发生突变故障时的故障容错方法展开研究，分析了残差χ2法的检测性能，给出了判断故障幅值大小的依据，指出残差χ2法不能用于小幅值突变故障检测，提出了一种基于衰减记忆思想的故障容错方法，在检测到故障后，构造“伪正常”状态，同时隔离故障量并重构量测方程，利用衰减记忆思想，增大新的无故障量测的权重，减小因未隔离故障量测信息的陈旧滤波值的权重。仿真结果表明，本文所提方法能够提高滤波精度，适用于故障多发的情况，对于增强系统可靠性具有重要意义。