基于Allan方差和SVR的MEMS陀螺仪随机误差分析与预测

付永恒，张丽杰

(内蒙古工业大学电力学院，内蒙古 呼和浩特 010051)

MEMS陀螺仪在低成本导航领域中应用前景广阔，但是其精度相对较低，因此需要对其随机误差进行补偿，以保证导航精度。对随机误差进行分析和预测是补偿的前提。MEMS陀螺仪随机漂移误差的分析主要有自相关函数法、功率谱密度法、基于时间序列分析的自回归平滑模型方法和Allan方差法[1-2]。Allan方差法能够对MEMS陀螺仪误差源统计特性进行有效的识别，而且计算简单、分析效果好[3-5]，IEEE协会将其定为分析光纤陀螺仪随机误差的标准方法[4，6]。支持向量机(SVM)是以统计学习理论和结构风险最小化建立起来的机器学习方法，在解决小样本、非线性问题上具有较高的推广能力和泛化能力，且克服了神经网络的局部极值、过拟合等问题[7-9]。支持向量回归(SVR)是在SVM的基础上发展而来的，主要用于回归预测。文献[10—11]将SVR算法用于陀螺仪误差预测，其预测精度要高于神经网络。

本文以ADXRS620 MEMS陀螺仪为试验对象，为了使SVR预测MEMS陀螺仪随机误差的精度更高，采用基于混合核函数和粒子群优化(PSO)参数的SVR算法对MEMS陀螺仪误差进行预测，并通过Allan方差法分析随机误差的效果。

1 MEMS陀螺仪随机误差分析

1.1 Allan方差分析法的基本原理

设采样间隔为t0，MEMS陀螺仪数据共采集了N个，可得陀螺仪数据的时间序列为{wt}，把采集的N个数据分成K组，K=N/M，其中每组包含M个数据，每组的时间间隔为t=t0M，第k个子集的平均值可以表示为[12]

(1)

对每个不同的平均时间间隔t，Allan方差的定义为

(2)

式中，〈〉表示求平均值。

量化噪声Q、角度随机游走N、零偏不稳定性B、角速率随机游走K、角速率漂移斜坡R为MEMS陀螺仪常见噪声。假设各噪声源相互独立，则MEMS陀螺仪随机误差的Allan方差为各类误差的方差和，即

(3)

MEMS陀螺仪实测数据绘制得到的Allan方差曲线通过最小二乘法进行拟合，可得到Ci，进而可计算得到各误差系数

(4)

1.2 陀螺仪随机误差分析

本文以美国ADI公司的ADXRS620单轴MEMS陀螺仪为试验对象，采用STM32F407ZET6对ADXRS620测量数据进行采集、处理和上传。将ADXRS620采集系统水平放置在转台上，在转台状态处于静止、转速改变、转速恒定3种状态时进行数据采集，采集频率为100 Hz，采集的数据如图1所示。

为了避免野点和信号趋势对随机误差建模的影响，进行Allan方差分析前，首先对MEMS陀螺仪静止状态的数据进行去野点处理；对转速改变和转速恒定时的数据进行去趋势项处理，之后进行去野点处理。MEMS陀螺仪不同状态数据的预处理结果如图2所示。

对图2中MEMS陀螺仪不同状态下的误差数据进行Allan方差分析，结果见表1。

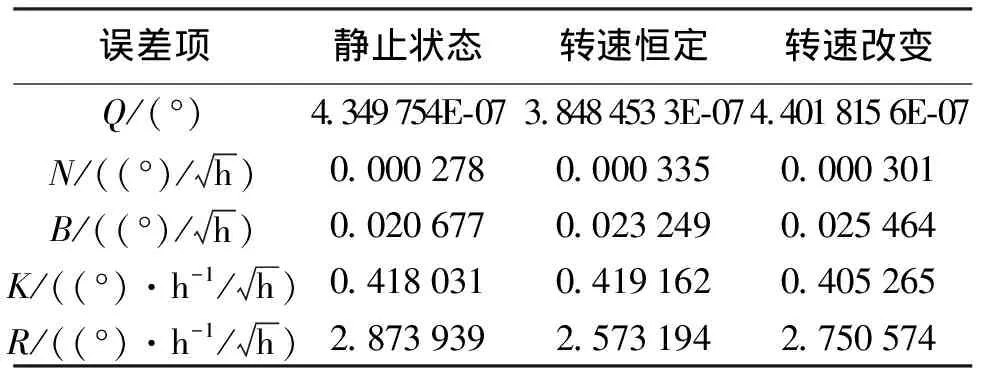
表1 误差项系数

由表1可以看出，角速率漂移斜坡噪声、角速率随机游走噪声和零偏不稳定性噪声是ADXRS620MEMS陀螺仪的主要噪声，其中角速率斜坡噪声影响最大；当MEMS陀螺仪处于不同状态时，其Allan方差误差项系数变动很小，因此可认为其噪声特性相同，因此可采用静止状态时的误差预测模型去预测MEMS陀螺仪处于不同状态下的随机误差。

2 基于SVR的MEMS陀螺仪误差预测模型

2.1 SVR的基本原理

SVR根据给定的训练样本和训练目标求得最优输入输出模型，并将该最优模型用于预测问题。假设训练样本为{xi}，训练目标为{yi}，二者的拟合关系为[13]

yi=wTφ(xi)+b

(5)

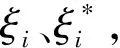
(6)

为了求解式(6)的有约束最优化问题，需要引入拉格朗日乘子α、α*，得到其拉格朗日方程式为

(7)

根据Wolfe对偶定理，可将式(7)转换为拉格朗日对偶问题

(8)

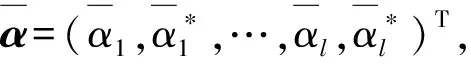
(9)

式中，[φT(xi)φ(xi)]表示高维空间中的内积运算。用核函数代替内积运算不仅可以减少内积的运算量，而且可以把低维空间中非线性不可预测问题转化为高维空间中的线性可预测问题，因此式(9)可进一步转换为

(10)

2.2 核函数的选择及参数优化

在SVR模型训练过程中，核函数和模型中的各项参数对SVR模型的预测精度影响较大，因此需要对核函数和参数进行选择。

常用的核函数有多项式核函数(Kpoly)、线性核函数(Kline)、Sigmoid核函数(Ksigmoid)和RBF核函数(Krbf)。Kpoly是一种全局性核函数，泛化能力强，但是学习能力弱；Kline是一种特殊的多项式核函数，具有多项式核函数的特性；Ksigmoid常被用作神经网络的阀值函数；Krbf是一种局部性核函数，学习能力强，但是泛化能力较弱[14]。

首先，核函数要满足Mercer条件，为了使核函数的学习和泛化能力最大化，本文构造了由Kline、Krbf和Ksigmoid混合的核函数

Kmix=m1Kline+m2Krbf+(1-m1-m2)Ksigmoid

(11)

影响本文模型预测精度有以下4个参数：

(1) 惩罚系数C。C影响SVR模型的泛化能力和预测精度。SVR模型的泛化能力随着C的减小而增强，但是SVR预测的精度会随着C的减小而变低[15]。

(2) 敏感损失值ε。SVR模型的预测性能由ε决定，SVR预测性能随着ε的增大而降低，但是ε太小容易出现过拟合现象。

(3) 核宽度σ。模型的推广能力由σ决定，SVR模型的推广能力随着σ的增大而增大，但是σ过大会降低预测精度。

(4) 权重系数m1、m2。m1和m2是调节Kline、Krbf和Ksigmoid可信度的系数。

为了提高随机误差预测精度，本文采用PSO算法对C、ε、σ、m1和m2进行寻优，PSO的适应度函数为训练数据三折交叉验证的均方根误差(RMSE)，即当交叉验证的RMSE最小时所对应的参数即为最优参数。

2.3 SVR预测模型的建立

在Matlab中建立MEMS陀螺仪随机误差的预测模型，建立步骤如下：

(1) 将预处理后的数据同时作为训练样本{xi}和训练目标{yi}，采用式(11)混合核函数将训练数据转化到高维空间中，将非线性不可预测问题转化为线性可预测问题。

(2) 通过PSO算法对不敏感损失值ε、惩罚系数C、核宽度σ，以及核函数权重系数m1、m2进行寻优。PSO算法的粒子速度函数和位置函数为

(12)

式中,ω为惯性权重；vkd为粒子的速度；xkd为粒子位置;n为迭代寻优的次数;r1和r2是0～1之间的随机数；c1、c2为学习因子；pkd为个体最优解；pgd为种群最优解。考虑到PSO算法的精度和待寻优参数的数目，本文设定c1、c2为2，种群个数为5，种群规模为60，种群迭代数为100，当达到最大迭代次数时即可得到ε、C、σ、m1、m25个最优参数。

(3) 将PSO算法得到的最优参数ε、C、σ、m1和m2代入SVR训练函数，求解式(8)中的凸二次规划问题，求得其最优解并将该最优解代入式(10)，即得到SVR预测模型。

3 试验及结果分析

3.1 MEMS陀螺仪误差预测SVR模型核函数试验

MEMS陀螺仪静止状态时的随机误差预处理数据，采用2.3节所述方法建立SVR预测模型，并与Kpoly、Kline、Ksigmoid、Krbf等单核核函数的预测结果进行比较，参数寻优结果见表2，预测结果如图3所示，预测结果的RMSE见表3。同时分析预测前后数据的Allan方差，误差项变动幅度见表4。

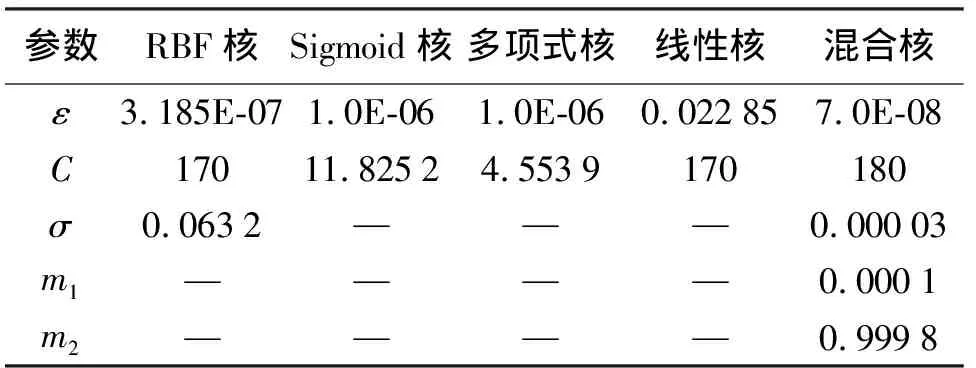
RBFSigmoidε3.185E-071.0E-061.0E-060.022857.0E-08C17011.82524.5539170180σ0.0632———0.00003m1————0.0001m2————0.9998

表3 静止状态预测结果的RMSE

表4 不同核函数预测结果ALLAN方差误差项变动幅度 (%)

由图3可知，Kpoly、Kline、Ksigmoid、Krbf和Kmix均具有较好的误差预测效果。由表3和表4可知，混合核函数Kmix的Allan方差误差项系数变动幅度是最小的，预测结果的RMSE较其他单核核函数小2～6个量级，仅为4.944 122E-11((°)·s-1)，因此本文构造的混合核函数SVR对MEMS陀螺仪随机误差预测效果要优于其他单核核函数。

3.2 MEMS陀螺仪误差预测模型一致性试验

采用3.1节中建立的MEMS陀螺仪处于静态时误差模型预测其转速改变和转速恒定情况下的随机误差，预测结果如图4、图5所示，预测结果的RMSE见表5。同时分析预测前后数据的Allan方差各误差项变化情况，结果见表6。

由表5和表6可知，采用陀螺仪静止状态时训练得到的预测模型预测其在转速改变和转速恒定状态下的随机误差，预测前后的Allan方差误差项变动幅度很小，总的预测RMSE不超过1.0E-11((°)·s-1),因此当陀螺仪处于不同状态下噪声特性相同时，则可采用统一的SVR预测模型预测随机误差，从而说明本文对MEMS陀螺仪处于不同状态时的随机误差的Allan方差分析结果有效。

RMSE/((°)·s-1)4.359299E-114.280525E-11

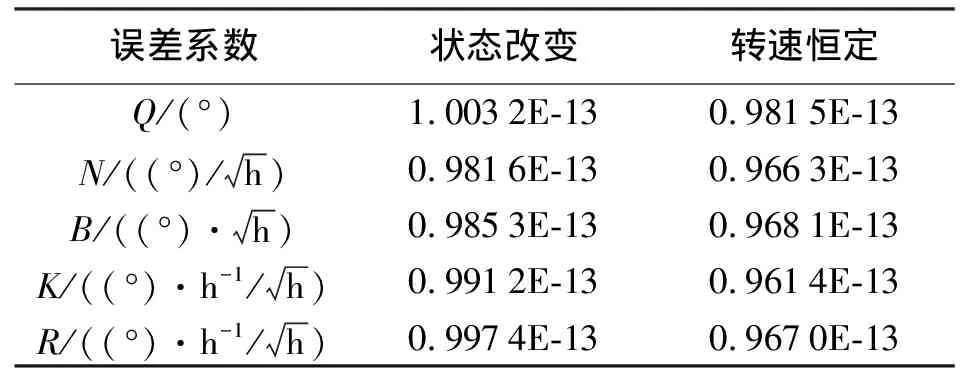
表6 转速改变和转速恒定误差项变动幅度 (%)

4 结 语

针对低成本MEMS陀螺仪数据精度低的问题，本文提出了一种结合线性核函数全局特性、RBF核函数的局部特性和Sigmoid核函数的神经网络特性的混合核函数，并通过PSO算法进行参数寻优的SVR随机误差预测算法，同时使用Allan方差法分析了MEMS陀螺仪SVR预测前后的随机误差噪声特性。试验结果表明，最优混合核函数SVR模型预测MEMS陀螺仪随机误差较单独核函数精度更高；当MEMS陀螺仪所处状态不同，但噪声特性相同时，可采用统一的SVR预测模型预测随机误差。本文研究结果可为SVR预测算法用于MEMS陀螺仪处于不同状态下随机误差实时补偿提供依据。