灰色-小波神经网络支持下对地铁工程沉降变形的预测

姜 刚，李 举，陈 盟，周佳薇

(1. 长安大学地质工程与测绘学院，陕西 西安 710064； 2. 西部矿产资源与地质工程教育部重点实验室，陕西 西安 710064； 3. 西安科技大学测绘科学与技术学院，陕西 西安 710054)

随着社会的发展，地铁成为人们生活中必不可少的交通工具之一。地铁的安全问题也逐渐引起人们的重视，因此如何利用有限的监测数据建立模型以快速分析预测将某一时刻的变形，阻止灾害的发生[1]是值得研究的热点问题。目前对沉降数据处理的方法有很多[2]，主要包括：回归分析、时间序列模型、灰色系统理论模型[3]、卡尔曼滤波模型、人工神经网络等[4-5]。文献[6]将小波神经网络和灰色模型结合在一起，在停车泊位上取得了较好的预测结果。本文提出将小波神经网络的理论和灰色系统理论结合起来，建立组合模型，利用呼和浩特市轨道交通1号线的沉降点观测数据，检验模型的稳定性，并分析预测数据的准确度和精度。

1 灰色系统理论[7]

1.1 GM(1,1)灰色模型

灰色系统理论是我国邓聚龙教授提出的一种数学方法。灰色系统理论是对原始数据进行处理，弱化其随机性，因此具有对原始数据质量要求不高、易操作的优点。此预测包括数列预测法、季节灾变预测法、拓扑预测法、系统预测法等[8]。根据地铁变形监测中数据的特点，本文选择的是数列预测法；考虑变形监测数据的特点，选择GM(1,1)模型。

(1) 原始沉降观测数列为:X(0)={x(0)(1),x(0)(2),…,x(0)(n)}，x(0)(n)为第n期观测值。

(4) 对此新序列建立白化方程

(1)

白化方程的解为

(2)

1.2 GM(1.1)模型精度评定[9-10]

本文仅对相对误差进行评定，评定其是否符合要求。

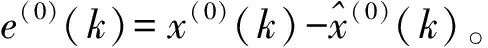
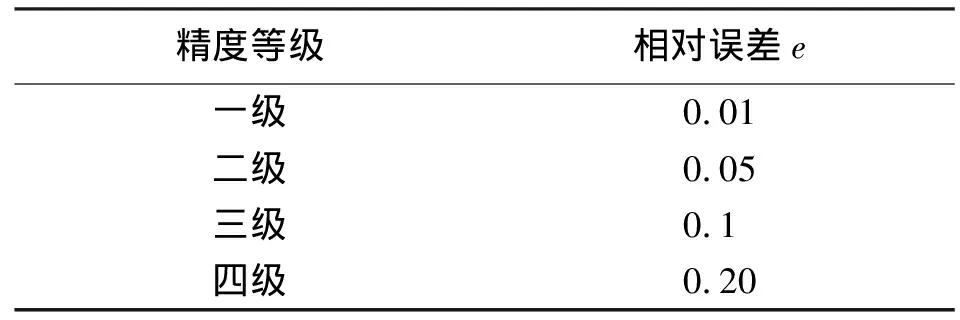
表1 模型精度评定标准

2 小波神经网络概述

人工神经网络是模拟大脑处理信息的模式，通过学习训练，找到输入数据和输出数据的关系，在处理背景不清楚的情况下可以显示其强大的能力。在变形数据非线性关系的诊断和预报中，由于沉降因素错综复杂，不能用准确的数学或力学模型表示，此时神经网络模型的优势就表现出来了。

2.1 小波神经网络模型结构

小波神经网络模型是在BP神经网络模型的基础上引入小波理论，利用小波函数代替隐含层的激励函数(sigmoid)，引入平移因子和尺度因子，使网络拥有更加高效的收敛能力和更好的模型拟合能力[11-12]。

小波神经网络预测模型一般分为3部分，即输入层、隐含层和输出层[13]。各层节点之间通过激励函数传递，之间存在连接权值。小波神经网络隐含层的激励函数利用小波函数，这点与BP神经网络不同，信号前向传播的同时误差反向传播，本文采用的是Morlet小波函数，其表达式为[14]

(3)

式中,f(x)表示加权和；β表示平移因子；α表示尺度因子。

小波神经网络输出层计算公式为

(4)

式中，wik为隐含层到输出层权值；h(i)第i个隐含层的节点输出；l为隐含层节点数m为输出层节点数。

小波神经网络权值参数修正算法是梯度修正法修正网络的权值和小波基函数参数，进而使小波神经网络预测模型的输出值不断地逼近期望的输出值。

小波神经网络算法训练步骤如下[15]：

(1) 网络初始化。对伸缩因子ak，平移因子bk，以及网络连接权重wik、wjk进行随机初始化，并设置学习效率η。

(2) 样本分类处理。样本分为训练样本和测试样本，网络模型需要先训练才能进行测试，测试网络预测的精度，将样本归一化后输入网络。

(3) 网络训练。输入训练值，计算预测输出值和输出值与期望输出值的误差。误差符合标准则输出预测值和权值。此时可以进行网络测试，输入测试值，输出预测值和误差。

(4) 权值修正。经过步骤(3)的计算，分析误差是否符合。若不符合，则修正网络权值和小波函数参数，使预测值更加接近期望输出值，不断进行训练修正，直至误差符合标准。

(5) 训练结束，得到预测值后，反归一化处理得到最终预测值。

小波神经网络输入层、输出层、隐含层节点确定：

2.2 小波神经网络模型类型[16]

从形式上小波神经网络可分为两大类：

(1) 小波分析与神经网络分离，称为辅助式小波神经网络。二者相互独立又紧密联系，小波分析作为数据预处理的过程，体现小波强大的去噪功能，输入神经网络的值实际是经过去噪后的数据，为网络模型去除了噪声。

(2) 将小波分析与神经网络结合在一起，将激励函数换作小波函数，这样的小波神经网络称为嵌入式神经网络。隐含层的激励函数用小波函数代替，相对应的输入层到隐含层的权值及隐含层阈值分别由小波函数的伸缩因子与平移因子代替。

3 工程实例分析

呼和浩特市轨道交通1号线一期工程中间某车站，位于街交口处，跨路口设置。此站采用地下两层单柱两跨的结构形式，采用明挖顺做法施工。在基坑开挖的过程中为了基坑、周围管线的安全，要对地表、管线和墙顶进行监测。

目前对于基坑的监测已经进行了多期的监测，并且仍在监测，此文选择地表监测点ZQC1、墙顶监测点ZCL9-1和管线监测点ZQS16，每个点选取39期数据进行分析。3个点的沉降量见表2。

表2 点ZQC1、点ZCL9-1和点ZQS16的沉降量 mm

点ZQC1、点ZCL9-1和点ZQS16 39期数据的走势图如图1所示。

随着地铁的修建，地形在不断改变，可能会影响监测点的沉降。而且环境、人为、仪器因素都会产生噪音，有可能导致观测值噪声比较大。因此沉降观测数据波动较大，与理论期望值相差较大。其沉降精度见表3。

0.050.150.51.5

3.1 灰色-小波神经网络模型结构

小波分析在时域和频率域有很好的局部化优点，可以很好地逼近非线性函数，因此小波神经网络强化了神经网络模型的优点，更合适学习局部非线性和快速变化的函数[17]。

文中采用的嵌入式的小波神经网络，采用Morlet函数。在小波神经网络处理数据之前，引入GM(1,1)灰色模型，建立综合数据处理模型。先用GM(1,1)灰色模型对数据进行预处理，然后将预处理的数据作为输入数据，原始观测数据作为期望输出数据。训练小波神经网络模型，对模型准确度进行分析。

3.2 工程应用

为验证灰色小波神经网络模型的正确性及优越性，本文选取呼和浩特市轨道交通1号线一期工程中间某车站，择地表监测点ZQC1的39期数据进行分析。选取前33期为训练样本，后6期与预测值进行对比分析。灰色模型与灰色小波神经网络模型预测结果对比如表4、图2、图3所示。

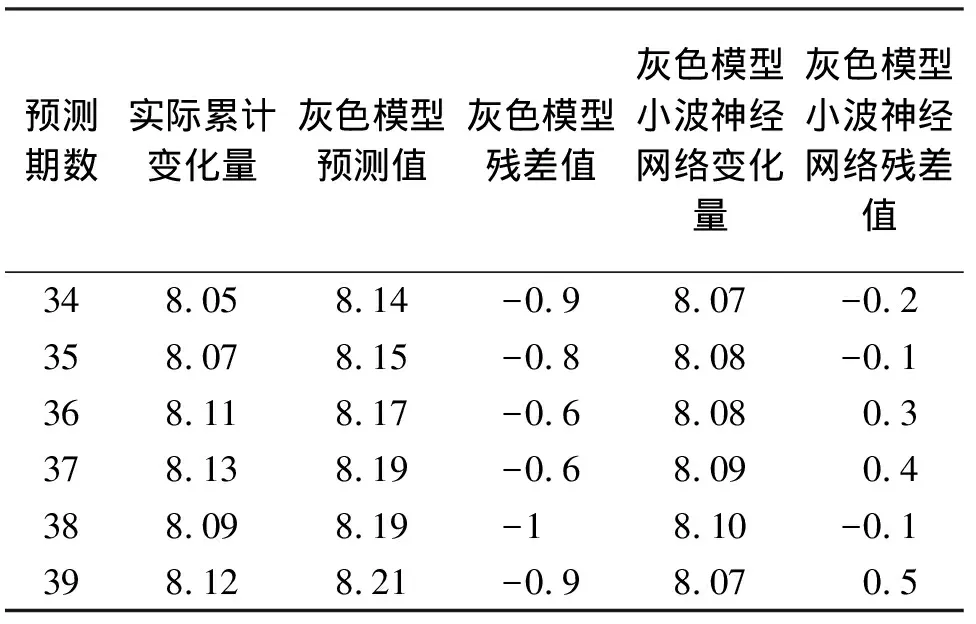
348.058.14-0.98.07-0.2358.078.15-0.88.08-0.1368.118.17-0.68.080.3378.138.19-0.68.090.4388.098.19-18.10-0.1398.128.21-0.98.070.5

分析表4可知，灰色小波神经网络模型预测值的残差值明显比灰色模型小，灰色小波神经网络模型更加接近实际值，其预测的优越性显而易见。灰色小波神经网络模型与灰色模型对比如图2所示，灰色模型的缺点显而易见：随着时间的推移其预测精度会越来越低，最后呈现发散的状态。而组合模型则很好地改善了这个问题。如图3所示的相对残差图可知，组合模型的相对残差大部分分布在-0.5至0.5之间，精度属于二级等级，预测值质量上满足要求。实例证明灰色-小波神经网络预测模型在对沉降数据的处理中，性能稳定，预测的准确度高，精度稳定。

4 总 结

本文对比了灰色小波神经网络模型和灰色模型，并对地铁监测点沉降进行了预测。发现两种预测模型所得的预测值与实际值相近，但灰色小波神经网络模型上预测精度和稳定性要明显高于灰色模型。结果表明，灰色小波神经网络模型相对于灰色模型可以提高预测精度和稳定性，更能提高预测结果，可为地铁变形监测提供更有价值的参考。