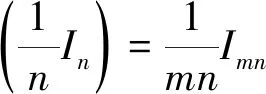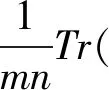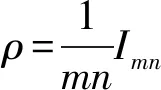保持量子态凸组合的Tsallis的映射
2019-06-04劳毅慧杨君齐
劳毅慧,杨君齐
(1.同济大学 数学科学学院,上海 200092;2.广西民族师范学院 数学与计算机科学学院,广西 崇左 532200)
1 问题的提出
量子态叫作密度矩阵,是作用在复希尔伯特空间上的半正定矩阵.一个量子态ρ是纯态当且仅当ρ2=ρ,即ρ是一个秩1 投影.若ρ2≠ρ,则量子态ρ是一个混合态.复有限维希尔伯特空间Hm的所有量子态记为S(Hm),它是个凸集.所有纯态记为Pur(Hm),显然Pur(Hm)是S(Hm)的子集.在量子信息学中,人们经常在多体环境上研究问题,这时多体系统复希尔伯特空间H可用子系统Hi(i是个自然数)的张量积表示.即
H=H1⊗H2⊗…⊗Hk
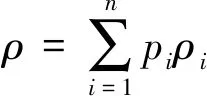
量子纠缠是量子信息学的一个基本物理概念,判断复合系统中一个量子态是否可分很重要也费力,于是找一个作用于量子态之间的能够简化量子态的映射的结构是有意义的.一直以来,多体系统中保持某一数值如冯诺依曼熵、数值域、p范数、幂等、点谱等的线性映射的结构有很多成果值得学习.2012年,Fošner等[1]对量子信息科学的线性保持问题做了一个概述,该文不仅刻画了保持谱不变的由埃米特矩阵张量积映射成埃米特矩阵张量积的线性变换的结构,还刻画了保持谱半径不变的矩阵张量积之间的线性变换的结构.很快,他们在文献[2]中也找到了保持Ky Fan范数和Schatten范数的矩阵张量积之间的线性变换的形式,并把结论推广到三体以上多系统环境.文献[3]也研究了类似的定义和问题,接着侯晋川等[4]把文献[3]的结果推广到无限维的情形.这些成果研究的算子之间的张量积的映射都是线性的.文献[5-6]研究的是关于量子测量如冯诺依曼熵、Tsallis熵单体系统上的非线性映射.在文献[7-8]中刻画了一个作用在双体量子系统H1⊗H2上的所有可分态之间的并保持凸组合的双射的结构.现在的目的是研究一个保持Tsallis熵凸组合的作用在量子态上的满射的结构.其中Tsallis熵的定义与性质可以在文献[9-10]中找到.对于ρ∈S(H)、r∈R+{1},Tsallis熵的定义如下:
下面是主要结果.
2 定理的证明
定理1设S(Hm⊗Hn)为复双体希尔伯特空间Hm⊗Hn上的密度矩阵的全体,其中Hm、Hn是维数分别为m、n(m,n≥2)的复希尔伯特空间.记Ssep(Hm⊗Hn)为其中可分量子态构成的凸集,映射
φ:S(Hm⊗Hn)→S(Hm⊗Hn)
是满射,而且
φ(Ssep(Hm⊗Hn))=Ssep(Hm⊗Hn)
若对于某个r∈R+{1},满射φ保持量子态凸组合的Tsallis熵
Sr(tρ+(1-t)σ)=Sr(tφ(ρ)+(1-t)φ(σ))
对于任意的ρ、σ∈S(Hm⊗Hn)和对于任意的t∈[0,1]成立.则Hm、Hn分别存在酉算子Um、Vn使得φ(ρ)=(Um⊗Vn)ρ(Um⊗Vn)*对于任意的ρ∈Ssep(Hm⊗Hn)成立.
证明定理1需要如下引理.
引理1(见文献[11]命题3.8)设H是复有限维希尔伯特空间,映射φ:S(H)→S(H)是满射,若对于某个r∈R+{1},满射φ保持量子态凸组合的Tsallis熵
Sr(tρ+(1-t)σ)=Sr(tφ(ρ)+(1-t)φ(σ))
对于任意的ρ、σ∈S(H)和对于任意的t∈[0,1]成立.则H存在酉算子或者是共轭酉算子W使得φ(ρ)=WρW*对于任意的ρ∈S(H)成立.
引理2(见文献[8]定理3.5)设Ssep(Hm⊗Hn)为复双体希尔伯特空间Hm⊗Hn上所有可分量子态的全体,其中Hm、Hn是维数分别为m、n(m,n≥2)的复希尔伯特空间,映射
φ:Ssep(Hm⊗Hn)→Ssep(Hm⊗Hn)
是双射.则φ保持凸组合当且仅当下面之一成立:
(1)存在可逆算子S∈B(Hm)、T∈B(Hn),使得
对于所有的ρ∈Ssep(Hm⊗Hn)成立;
(2)存在可逆算子S∈B(Hm,Hn)、T∈B(Hn,Hm),使得
对于所有的ρ∈Ssep(Hm⊗Hn)成立.
其中ψ有如下几种可能:恒等算子、转置,有对第一个系统的转置和对第二系统的转置,其中转置和部分转置可相应于双体空间的任一组积态基来取.θ为有界自伴算子Bsa(Hm⊗Hn)上的对换,即满足θ(ω⊗τ)=τ⊗ω的线性映射.
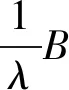
证明 由条件知
Imn=(A⊗B)(A⊗B)*=(AA*)⊗(BB*)
设AA*=(dij),则Imn=(dijBB*).从而必须所有的dij(i≠j)都为零,且所有的dii(i=1,2,…,m)都相等且非零,记其为α,于是αBB*=In、AA*=αIm.类似地,考虑
Imn=(A⊗B)*(A⊗B)=(A*A)⊗(B*B)
可知存在某个非零数β使得βBB*=In、AA*=βIm,于是α=β.特别地
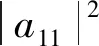

定理1的证明 由引理1知,φ必形如φ(ρ)=VρV*,其中ρ∈S(Hm⊗Hn),V为Hm⊗Hn上的酉算子或共轭酉算子,从而φ是可逆的.又知
φ(Ssep(Hm⊗Hn))=Ssep(Hm⊗Hn)
因此当φ限制在可分态上时,它满足引理2的条件.下面先考虑引理2的第一种情况.综合引理1和引理2的结果,在Hm⊗Hn存在酉算子或共轭酉算子V,使得对于任意的ρ∈Ssep(Hm⊗Hn)有

接着将