从句法到语用： 隐喻的真值条件

黄华新 洪峥怡

(浙江大学 哲学系， 浙江 杭州 310028)

一、 隐喻的语义真值条件

真值反映了命题与事态之间的对应关系，传统的真值条件分析严格限制在字面语义与世界状态的符合之上。因此，表达非字面意义的隐喻语句在很长时间内被简单地视为语义上真值为假。如经典的格赖斯理论认为，隐喻违反会话合作原则中质的准则。由于语义上不符合逻辑，它在真值上为假(两个所指的某些性质之间不匹配)，并由这种逻辑上的假产生有意义或有见识的陈述[1]52，也就是它本身并没有“说”什么，而只是给出了一种“好像要说某事”的含义，以此作为传达说话者含义的工具。

随着隐喻研究的认知转向，学者们逐渐意识到，隐喻不仅是一种修辞手段，更是一种认知方式。莱考夫(G.Lakoff)和约翰逊(M.Johnson)在《我们赖以生存的隐喻》开篇就指出，“日常生活中隐喻无处不在，我们的思想和行为所依据的概念系统本身是以隐喻为基础的”[2]1。作为一种基本的认知方式，隐喻必然有它要表达的特定语义，也就会有真值。“通过隐喻映射来理解真与通过非隐喻映射理解真不存在本质上的区别。唯一的不同是隐喻映射涉及通过某一事物来理解另一事物，而非隐喻映射只涉及一件事物。”[2]154实际上，真值条件应该是隐喻语句的一部分，听话人即使理解了说话人的会话含义，也可能否定他所使用的隐喻。

对隐喻真值条件的刻画主要有两条路径[3]。20世纪90年代，格勒克斯堡(S.Glucksberg)等人提出了范畴归属理论(Category Attribution Theory)，认为隐喻语句的理解过程是一个范畴归属判断过程。“在隐喻中，喻体词有两个潜在的指称对象：一个是字面指称，另一个是以该喻体为代表的事物或情境的类范畴。如果这个范畴被用于描写一个隐喻本体，那么它就起到赋予隐喻本体以特征的归属性范畴的作用。”[4]1542此后，吉纳比(J.Genabith)提出了一种与上述范畴归属理论的思想有着内在一致性的隐喻真值刻画方式，他运用建立在λ演算基础上的高阶逻辑，通过标准类型论来描述范畴，由此探讨了隐喻语句的真值条件问题[5]45。具体而言，一阶语言主要描述的是个体的性质及个体间的关系，如果用它来刻画隐喻语句John is a fox，得到的是fox(j)|[fox(j)]=1 iff[j]∈[fox]，也就是句子的字面意思。显然John是一个人，不属于“狐狸”的个体集。而高阶语言则可以描述性质及性质间的关系。通过这种提升，可以进一步提取谓词中的某性质P，这是比本体和喻体都更高一个层次的类的属性，P性质的抽象类范畴同时包含了本体和喻体。上例的隐喻语义可以刻画为∃P(Pj∧∀x(foxx→Px))，意思是，存在一个性质P，John具有该性质，且任何狐狸也都具有性质P。隐喻语句的真值条件也就是本体和喻体真包含于一个抽象的类范畴，这一思想非常具有启发性。但正如吉纳比本人所言，他所做的工作只是针对隐喻意义的真值条件，并不是解释隐喻的处理过程[5]47。也就是说，这样的真值条件判定只是隐喻理解的最低要求。

不同于吉纳比的方案，斯坦哈特(E.C.Steinhart)提出了一种基于可能世界语义学来讨论隐喻的“隐喻结构理论”(STM)。他认为每个隐喻都具有模糊性:它同时具有字面真值条件(LIT)和隐喻真值条件(MET)。隐喻真值条件可以通过可能世界语义学和扩展的谓词逻辑进行刻画。他将源域和目标域视为不同的可能世界，将情境的可类比性作为可通达关系。以“AisC”式隐喻为例，用T标识目标域，S标识源域，MET标识不属于前两者的隐喻标志词，得到：((A)T(is)MET(C)S)MET。该表达式为真，当且仅当(∃B,D)(∃R)(R(A,B)&R(C,D))。意思是存在个体B、D和关系R，并且A和B之间的关系与C和D之间的关系均为R[6]178-179。斯坦哈特引入“可能世界”的概念，给隐喻真值条件研究提供了更大的空间，但该方案所立足的是可类比性，即把相似和对应作为隐喻的基本条件。隐喻是“通过另一事物来理解和体验当前事物”[2]3，相似性固然是一种重要联系，但关联并不唯一取决于相似性，不同语境下事物间的相似性程度也有很大差别，因此当处理源域与目标域的可类比性不高的隐喻句时，该方案可能会出现偏差。

纵观上述两种路径，吉纳比是通过两个类之间的包含关系来表征隐喻的跨域性，而斯坦哈特则是通过情景之间的对应来表征，两者对隐喻的作用机制理解有所不同。有学者已指出，吉纳比的方案以隐喻理解的结果为分析出发点，而斯坦哈特则以隐喻理解的过程为分析基础[3]97。但无论是哪种路径，所刻画的都是纯粹的语义真值条件，并不谈论如何从语句的生成角度分析这一语义真值条件的产生，也未把语境作为影响真值条件的重要因素。如果把语义真值条件的分析延伸至句法和语用，形成三者的交织和互动，或许可以更好地反映隐喻的生成和理解。

二、 隐喻的语用真值条件

诚然，纯粹语义是真值条件判定的核心，但在语言使用中，语句的真值条件往往超出语义层面。如在含有代词的语句中，必须先在语境中为代词赋值，才能判定这句话的真值条件。进而真值条件语用学提出，真值条件内容不仅可能(像在语境中为指示语赋值那样)受到饱和过程(即在语境中为特定表达式赋值的一种语用过程)的影响[7]5-6，而且会受到自由语用过程的影响。即在不需要填补空缺的语句中，仍然存在一种强语用效应对真值条件内容产生影响[7]7。

相应地，在对纯粹语义的刻画中，基本前提是认为自然语言的语义遵循“组合性原则”，语句是其各部分语义的函数，各部分语义组合成完整的语义。之后，蒙太格(R.Montague)构造了一个逻辑严密的部分语句系统，成为对语义组合性原则的成功尝试[8]。而真值条件语用学对这种语义组合性原则提出了质疑，雷卡纳蒂(F.Recanati)在《真值条件语用学》中指出，表达式(在语境中)经过调适(modulation)的意义产生于把在语境中恰当的调适函数应用于表达式的语义理解中，复杂表达式的语义内容是其组成部分调适内容(及其组合方式)的函数，但并非各部分语义内容(及其组合方式)的函数[7]49。其实就本质而言，这并没有完全否定组合原则，只是增加了一个调适过程，将字面义转化为调适的语义后，再进行组合。由此他引入了一个调适函数f，该函数以语境c为自变量，得到表达式在该语境下的解释。对语境敏感性表达式(指示语等必须依赖语境才有语义真值条件的表达式)来说，语境对词汇的指派是直接的，该规则可以写成：I(α)c=f(c)[7]41，即对表达式α来说，它可以用于组合的语义是在语境c中经过调适产生的某种内容f(c)。

隐喻的本质是通过彼概念来理解此概念的一个方面，这种迁移必然会使我们聚焦于某一概念的某一方面，而隐藏此概念的其他方面[2]7。比如常见的“争论—战争”隐喻，就是选择了战争所具有的战斗性特征，以突出争论的战斗性。隐喻的不确定性和动态性正是因为这种焦点性质的选择可能并不唯一。因此，隐喻的构建是一个动态过程，隐喻的真值判定也是动态的。戴维森(D.Davidson)认为，“真作为一种特性，不是语句的特性，而是说话方式、言语行为的特性，即关涉到语句、时间和人的有序三元组”[9]319，可见，时间、话语使用者等具体动态的语用因素对语用真值条件都有重要影响。因此，隐喻句虽然不属于一般的语境敏感，但语境导致了语句中出现明显的范畴冲突，迫使人们做出偏离字面意义的解释[2]45，语境在该机制中的作用与它对语境敏感性词汇的作用并没有本质区别。

帕金(P.Pagin)等提出可以递归地给出用于解释“调适M”的函数[10]46-50，雷卡纳蒂则将其具体表示为：M(e,c)=mod(e,c)(I(e)c)[7]49，其中e为表达式，c为语境，I(e)c表示语境c下对表达式e的字面语义解释。由该公式可见，表达式的字面义e具有双重属性：一方面，它和语境c是函数mod的自变量，二者一旦产生冲突，就会得到一个语用函数g(g=mod(e,c))；另一方面，它又是语用函数g的一个自变量，运算后的函数值为调适后的语义，表达在语境中凸显、相关或适当的语用效果。在分析“城市睡着了”[注]例句来自Recanati F., Literal Meaning, Cambridge: Cambridge University Press, 2004, p.34。这一语句时，雷卡纳蒂用该函数对“城市”一词的语义进行了调适，得到了语句的转喻义。同样对这一语句，如果我们将表达式“睡着”作为调适函数自变量，得到的将是隐喻义。

(a)“睡着”作为一种生命体特有的行为与“城市”这个无生命的事物产生了语义冲突，产生了语用函数g来实现对隐喻的理解:

mod(睡着,c)=g

(b)“睡着”也直接提供了字面语义，当输入的表达式是隐喻中与睡觉相关的源域，输出的就是隐喻的目标域，“睡着”这一字面义经隐喻调适后的语义就是“沉静而几无活动”:

M(e,c)=mod(e,c)(I(e)c)=g(I(e)c)=g(“睡着”)=沉静而几无活动

真值条件语用学通过引入调适函数，对不系统的语用因素进行了系统的阐释。只是直值条件语用论者认为上文所述的语用函数g完全出现在元语言层面，语用过程不由句法变项或任何类似的东西触发，而纯粹由语用原因产生[7]140。同时，他们又承认复杂表达式的语义内容是其组成部分调适内容(及其组合方式)的函数，即语句最终的语义还是通过函数组合实现的。为处理该矛盾，我们允许g这一元层面的函数出现在语义组合过程中。对于一个隐喻语句，如果存在既不属于源域也不属于目标域的隐喻标志词(如“AisB”型隐喻中的is)，则该词的语义为一个隐喻函数；如果语句中不出现隐喻标志词，则源域表达式本身具有双重语义，其一是字面意思，其二是在语境作用下产生的隐喻函数。由于这两种形式同时存在，为说明方便，可以视为表达式B自带一个不显示在表层语句中的隐喻函数，具体实现方式将在下文详述。

三、 隐喻真值条件的句法生成

蒙太格在20世纪70年代提出自然语言和形式语言在本质上并无差别，两者都遵循同样的法则，都可以统一在“普遍语法”的模式下进行精确的数学描述。他认为句法和语义同构，句法结构和语义表达的生成一一对应[8]。在这些原则下诞生的蒙太格语法开创了自然语言逻辑的研究范式，之后各流派几乎都继承了这一思想，大都认同句法和语义的生成是组合性的，在多数语句中句法和语义的同步生成是可能的。

范畴语法集中体现了这一思想，作为一种词汇语法，它首先为每个词规定范畴，再由范畴的组合生成语句。范畴包括初始范畴(原子范畴)和函子范畴。初始范畴如NP(代表名词短语范畴)和S(代表语句范畴)。函子范畴则如S/NP和SNP，表示输入的论元范畴为NP，结果范畴为S，即该范畴和一个名词短语组合后得到一个语句。S/NP为向前函子，论元NP在其右边出现;SNP为向后函子，论元NP在其左边出现[注]本文采用组合范畴语法的记法和规则，参见Steedman M.,″Combinatory Grammars and Parasitic Gaps,″ Natural Language & Linguistic Theory, Vol.5, No.3(1987), pp.403-439;邹崇理等《自然语言信息处理的逻辑语义学研究》，(北京)科学出版社2018年版。。

定义(范畴)：范畴集CAT是满足以下条件的最小集合[11]122。

(1)S,NP,IV,CN为范畴；

(2)如果A和B为范畴，则A/B和AB也是范畴。

同时，根据弗雷格(G.Frege)等人提出的组合性原则，自然语言的语义是其各部分语义的函数，通过类型论可以描述这种语义的生成过程。在类型论中，语言表达式分别属于不同的语义类型。根据自然语言的特点，定义个体表达式的类型为e(个体)，命题的语义类型为t(真值)。

定义(类型)：类型集T是满足以下条件的最小集合[11]105。

(1)e和t为基本语义类型；

(2)如果α和β为语义类型，则〈α,β〉也为语义类型。

可见，语义和句法的定义用到的是非常类似的函数运算，范畴语法的一条主要原则是：一个表达式的句法范畴反映了它的语义功能。如果在范畴和类型之间定义对应关系，也就间接得到了句法和语义的对应关系。因此可以定义一个将范畴映射到类型上的函数f：

f是一个从CAT到T的函数，并满足：

f(S)=t,f(NP)=e,f(CN)=f(IV)=〈e,t〉

f(A/B)=f(AB)=〈f(B),f(A)〉[注]蒙太格语法运用的是一种内涵范畴论，此处不考虑内涵和外延的区分，故进行简化。[11]196

这种句法和语义匹配的方法对计算机生成和理解自然语言十分有益。但对隐喻句而言，这种句法和语义的一一对应会遇到困难。从上述对隐喻真值条件的探讨中可以看出：同一语句存在着字面义和隐喻义两种合法的语义。当我们按照通常的做法给出句法和语义，生成的只能是语句的字面义，语句欲表达的隐喻义无法被刻画。

例1：张三是猴子。

图1是例1的语义刻画。

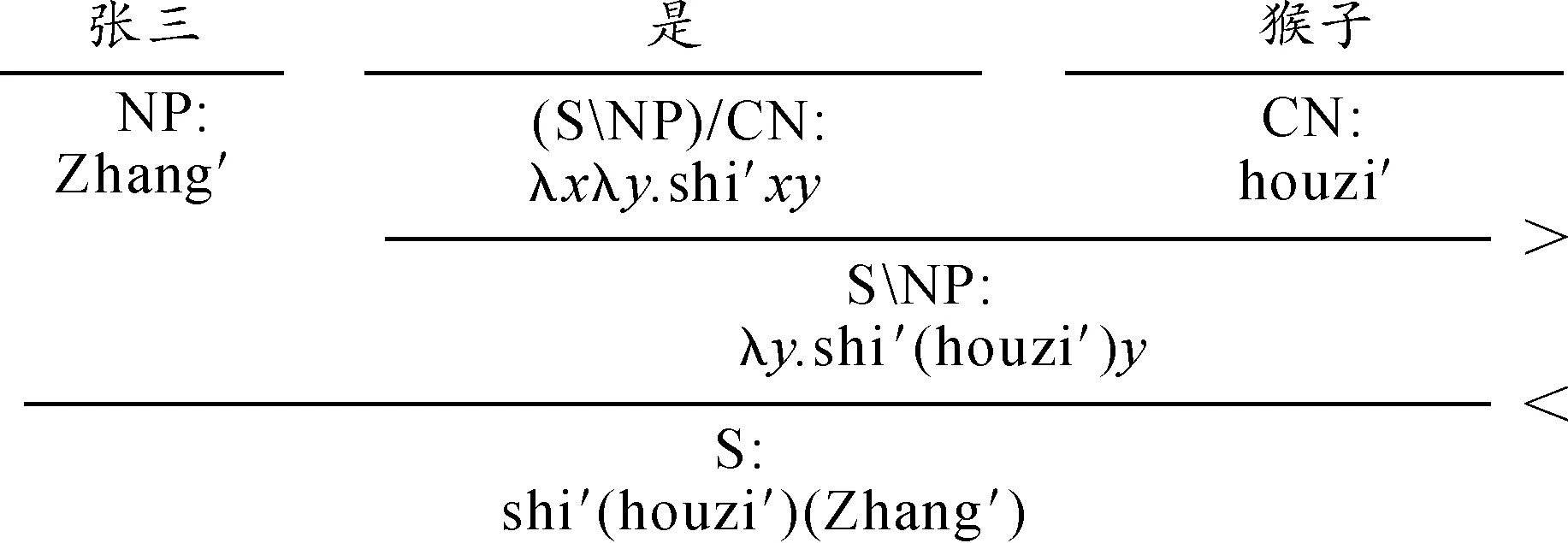
图1 “张三是猴子”的语义刻画

这里的判断动词“是”与其后的名词短语贴合，得到的短语“是猴子”在语句中充当谓词。从集合论上看，它是所有“猴子”个体的集合，表达“猴子”所具有的性质。这个谓词作为函数进一步与专名“张三”贴合，就得到了完整的语句，其真值条件可以表达为：‖张三是猴子‖=shi′(houzi′)(Zhang′)=1 iff‖Zhang′‖∈‖shi′(houzi′)‖，即有一个由猴子个体组成的集合，个体“张三”是该集合的元素，也就是有一只名叫张三的猴子。这里的“张三”是一个人，显然命题为假。

诚然，绝大多数可以有效使用的隐喻语句在字面解释下都为假，但根据上文所述，通过增加对语义的调适，组合原则依然有效，那么其真值条件也依然可以对应于句法而生成。为了合理解释隐喻语句，我们可以考虑为隐喻语句增加特有的标记，赋予不同的范畴，以另一种范畴组合方式实现隐喻语义的生成。

在范畴归属理论和吉纳比的真值判定方法中，存在一种高于源域概念和目标域概念的性质，隐喻句为真是因为存在这种二者共有的性质，这需要高阶语言来表达；而在雷卡纳蒂的调适方案中，表达式与语境产生冲突后会产生语用函数g，g的功能是将表达式从字面义转化为语境义，只是他没有表征这一转化是如何实现的。

我们从范畴类型理论的角度整合和完善这些尝试，进一步将该函数拆分为源域类型转换和隐喻函数选择这两个过程。具体做法是将源域中对象由个体集转换为(该对象所具有的)性质的集合，再通过受语境影响的从性质集到个体集的隐喻函数fc(语形上可能为空)，以上述性质集作为自变量，映射到其中一个性质，隐喻的判定就是目标域的对象是否为这个个体集中的元素，即目标域对象是否具有函数运算得到的那个性质。以“A是B”式隐喻为例，首先源域B从个体集提升为性质集，并将“是”视为一个从性质集到个体集的隐喻函数，也就是在B所具有的性质中进行选择。最终对“A是B”的真值条件判定就变为：‖A是B‖=1 iff A∈‖是B‖，其中‖是B‖变为B具有的某种性质。依照这一思路，重新给语句中成分赋予范畴，改变与之一一对应的语义类型，就可以实现语义上的改变。回到上述例子：

张三是猴子。⟹([张三]T[是]MET[猴子]S)MET。[注]下标记法参照Steinhart，其中S标识源域，T标识目标域，MET标识隐喻标志词和隐喻语句。

通过生成树给出句法范畴的贴合过程，见图2：

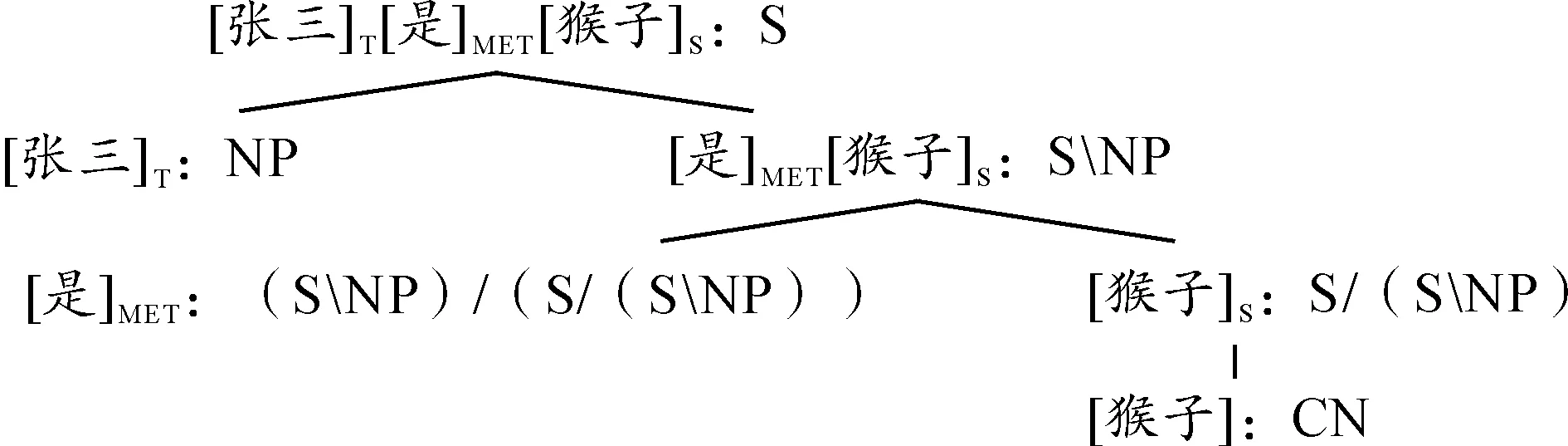
图2 “张三是猴子”的句法范畴

根据f(S)=t，f(NP)=e，f(A/B)=f(AB)=〈f(B),f(A)〉三条规则，得到与句法范畴一一对应的语义类型，见图3。

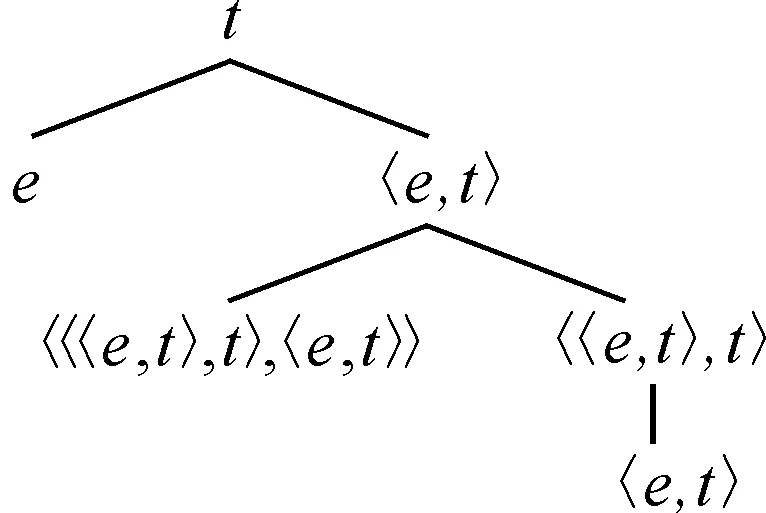
图3 “张三是猴子”的语义类型

“猴子”是一个通名，在类型上和不及物动词一致，相当于猴子个体组成的集合(即“猴子”这一性质)。当成为隐喻语句的源域时，其范畴转变为〈〈e,t〉,t〉，即性质的集合，且这一性质集的元素是所有(典型)猴子具有的性质。“是”的隐喻语义是一个语境影响下从性质集到个体集的函数fc，其定义域为各种名词提升后形成的性质集的集合，值域为个体集(性质)的集合。从语义类型角度看，输入类型为〈〈e,t〉,t〉的“一只猴子”后，得到的函数值类型为〈e,t〉。再输入一个类型为e的个体，得到完整的语句。

在范畴贴合的框架下添加以λ演算的形式来表达上述类型的语义，见图4：

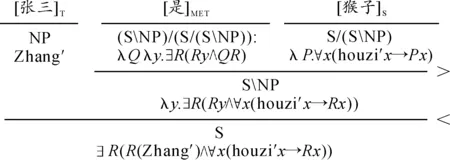
图4 “张三是猴子”的λ演算形式

“是猴子”的语义是一个从所有猴子都具有的典型性质构成的集合中选出的一个特征性质Xi，如果“张三”是这个集合中的元素，即张三具有这一典型的猴子特征，则语句为真。“张三是猴子”的语义是∃R(R(Zhang′)∧∀x(houzi′x→Rx))，直观意思是存在一个性质，张三具有该性质，且任意猴子都有该性质。

“A是B”式隐喻中，“是”既不属于源域也不属于目标域，它本身是隐喻标志词，也就是隐喻函数。而在非“A是B”式的复杂隐喻中，可能所有词汇都属于源域或目标域，这时可以认为类似于“是”的隐喻标志词在表层语句中以隐性的形式出现。

例2:我的车喝饱了油。⟹([我的车]T[()]MET[喝饱了]S[油]T)MET。[5]50

其中“喝饱了”除了字面意义，还能在语境作用下调适为隐喻的语用函数，表达为生成“()”这样一个隐性的隐喻函数。下面通过生成树给出句法范畴和与之匹配的语义类型，见图5。

在范畴贴合的框架下添加以λ演算的形式表达上述类型的语义，见图6。

这一隐喻中，源域中的对象是一种生物和液体之间的关系“喝”，目标域中的对象是汽车和汽油之间的关系R。首先对源域中的对象提升，得到“喝”这一关系所具有的性质的集合。以该集合为自变量，隐喻函数的函数值为“喝”具有的某个性质。如果关系R是这个集合的元素，则语句为真。“我的车喝饱了油”的语义是∃R(R(che′,you′)∧∀uv(he′(u,v)→R(u,v)))，直观意思是存在一种关系，“我的车”和“油”之间具有该关系，且任意满足“喝”这一二元关系的有序对都满足该关系。

上述过程刻画了隐喻语句的范畴组合和语义生成，最终得到的是与吉纳比的分析一致的真值条件；同时进一步分解了一个表达式转化为隐喻语用函数的具体过程，即通过对隐喻源域的范畴进行转化，得到范畴归属理论所要求的高阶性质，再通过一个语境相关的隐喻函数fc从性质集到个体集的运算，选取性质集中适应语境的元素。该选择依赖的是语境的关联性。关联是隐喻语用真值条件开启的关键因素[12]74，在隐喻语句的构造和理解中，双方都设想语句与语境存在关联，说话者相信听话者可以基于语境的关联性在源域提供的性质集中选出他所意欲表达的那个性质，而听话者也尽力根据语境提供的信息从性质集中选择最可能的元素。如“张三就是只猴子”，由“猴子”的语义得到的性质集中包括了猴子具有的所有典型性质：{哺乳动物，爱吃香蕉，顽皮好动，灵活……}，如果语境是老师批评不遵守课堂纪律的学生，则这句话是对“张三”这个人课堂表现方面的评价，因此选出的是可以用来描写人的品行特征的性质，得到“顽皮”这一属性，这句话的真值判定就变成，如果张三具有“顽皮”这一性质，则语句为真。正是基于这种关联性，交际双方才可以从语境中有效地提取信息，听话者得以识别说话者的意图并对隐喻做出符合说话者的理解。这就是语境c作为论元输入调适函数mod产生的作用，在语义的形式刻画中，这种作用可以进一步表现为支持函数在性质集中选择最理想的性质，实现隐喻语句的语义解释。

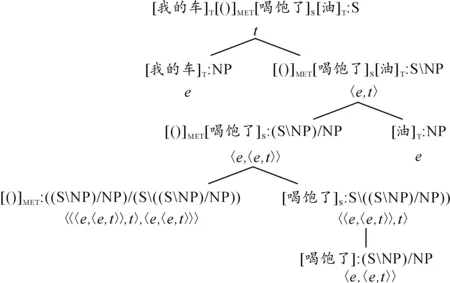
图5 “我的车喝饱了油”的语义类型

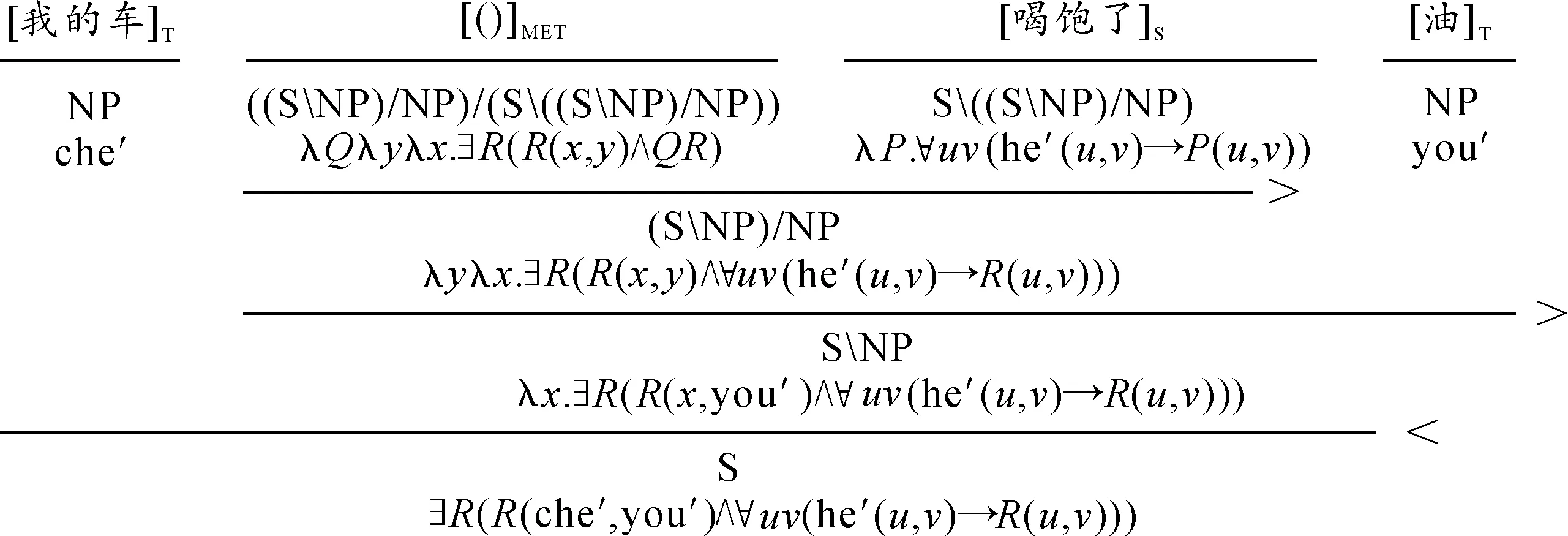
图6 “我的车喝饱了油”的λ演算形式

隐喻语句的语义有着非字面性和不确定性等特点，其语义内容并非各组成部分语义内容(及其组合方式)的函数，而是各组成部分经调适的内容(及其组合方式)的函数。但它仍然可以通过范畴的贴合从词汇产生语句，并由与之一一对应的语义的生成机制得到非字面的语义真值条件。在部分表达式的调适过程中，语境至关重要，它作为调适函数mod的一个自变量，生成不同类别的语用函数(包括解释隐喻义的函数)。在范畴类型理论框架下，这种语境的调适体现为转变源域类型和限制隐喻函数对性质的选择，从而对语句的真值条件产生影响。本文给出新的句法范畴和语义类型组合，一方面有利于机器理解隐喻语句时得到非字面的语义，另一方面能更清楚地分析语句的各成分在隐喻中起到的作用。