问题规约法在解决刚体动力学问题中的应用

许英姿 沈玉凤 李丽君

摘 要 根据人工智能中知识的表示方法，结合最近发展区理论，运用逆向思维的思维方式对理论力学中单自由度刚体系统动力学普遍定理综合应用问题的求解进行了探讨。

关键词 问题规约 最近发展区 逆向思维中图分类号：O311.2                                   文献标识码：A    DOI：10.16400/j.cnki.kjdks.2019.04.011

Abstract According to the knowledge of artificial intelligence methods， combining the theory of the recent development zone， using reverse thinking， and discussing the rigid body dynamic problems in theoretical mechanics

Keywords problems statute; recent development zone; reverse thinking

1 问题的提出

动力学普遍定理的综合应用问题，是单自由度刚体（系统）动力学问题的一个重要組成部分，[1]是指将动量定理（包括质心运动定理），动量矩定理（包括刚体绕定轴转动的微分方式、刚体的平面运动微分方程）和动能定理以及守恒形式（动量守恒、对固定点（或轴）的动量矩守恒、机械能守恒）进行综合应用。由于普遍定理中每个定理都有其不同的特点，因而在综合应用时，绝大部分同学都感到学习起来特别困难，更有甚者考试时看到动力学综合应用的题目就撒手不做。为了解决这一问题，将维果茨基提出的最近发展区理论[2-3]应用到课堂教学中，寻找出要解决的问题与学生已经掌握的普遍定理之间的最近距离。如何寻找这个最近距离就成为解决问题问题的关键所在。

问题规约法是人工智能所描述的知识表示的方法之一，[4]所谓问题规约法就是已知一个问题的描述，通过一系列的变换，将此问题最终变为一系列子问题的综合，这些子问题可以直接解决，从而解决初始问题。问题规约法的实质就是从目标（即要解决的问题）出发，逆向推理，建立子问题，以及子问题的子问题，直至最后将初始问题规约为一个本原问题的集合。

按照最近发展区理论，结合问题规约法，根据获取知识的一个途径，将大的困难拆分成小的困难，将解决问题的最近距离定义为一个子问题与另一个子问题之间的距离，再运用简单的逻辑推理，来解决复杂的问题。

2 应用

2.1 总结

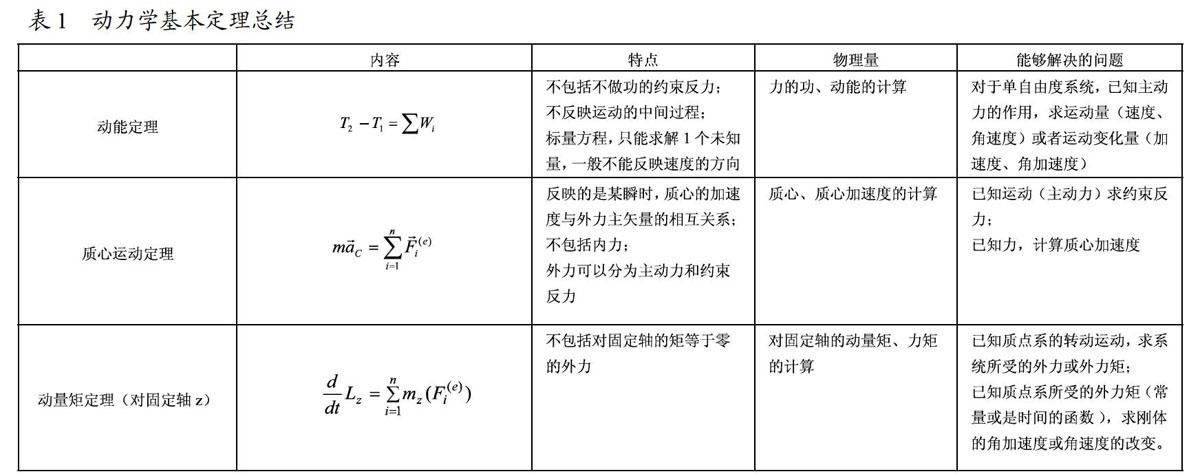
要想灵活地综合应用动力学普遍定理，首先应该深刻理解并掌握各定理的内容和特点，包括每个定理中有那些物理量，相关的物理量如何计算，能够解决什么问题等等。以动能定理（积分形式）和质心运动定理以及动量矩定理（对固定轴）为例，列表说明（表1）。

2.2 问题规约法应用

解决问题的关键是选择合适的定理，定理的选取一般是从所求的物理量出发，根据每个定理的特点，逆向推理，建立子问题，以及子问题的子问题，最后找到解决问题的思路。

2.3 算例

下面通过实例说明如何应用问题规约法求解单自由度刚体系统动力学的综合应用问题。

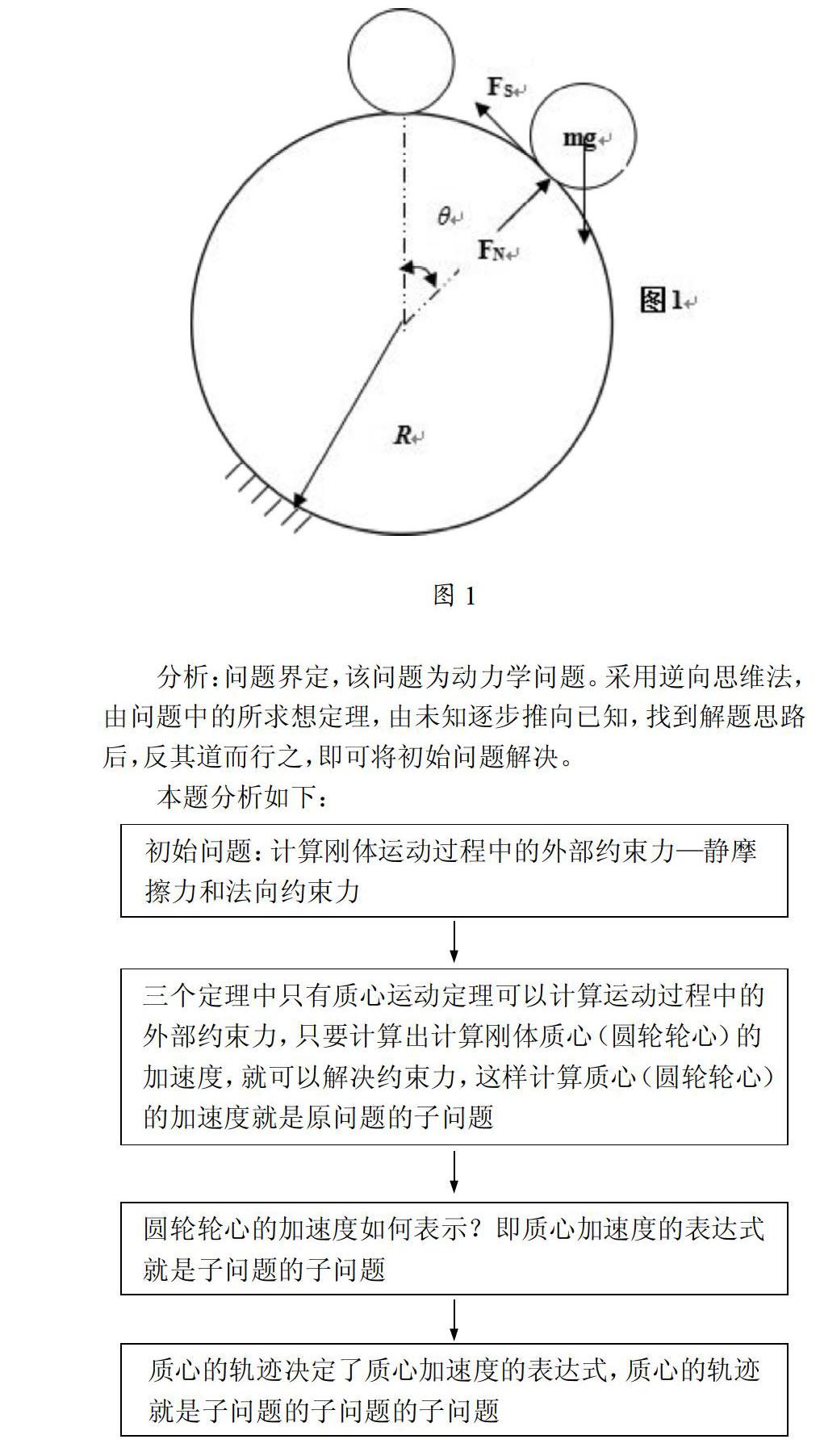
如图1所示均质圆轮质量为m，半径为r，静止在半径为R的固定圆柱的最顶端，受微小扰动后沿固定圆柱纯滚动。要求计算圆轮滚动到图示位置（不脱离固定圆柱）时受到的静摩擦力和法向反力。

分析：问题界定，该问题为动力学问题。采用逆向思维法，由问题中的所求想定理，由未知逐步推向已知，找到解题思路后，反其道而行之，即可将初始问题解决。

本题分析如下：

原问题归结为圆轮质心的运动的轨迹问题，而圆轮质心是以固定圆柱的轮心为中心，以为半径的曲线运动。圆轮质心的加速度，实质上是圆轮质心的切向和法向加速度;此时原问题就规约为计算质心的切向加速度 和法向加速度两个子问题。

根据运动学的知识，圆轮质心的法向加速度大小 （1）

式（1）中的%r是圆轮的角速度

圆轮质心的切向加速度大小 （2）

式（2）中的%Z是圆轮的角加速度。

分析：圆轮沿固定圆柱纯滚动为单自由度运动，约束力不做功，只有主动力重力做功，要计算圆轮由固定圆柱的顶端由静止开始运动到任意位置（不脱离固定圆柱）的角速度%r，显然用动能定理可以解决，而圆轮的角加速度%Z则可以通过对任任意位置的角速度求一阶导数获得。

这样就将一个复杂的原问题，规约为求圆轮在任意位置（不脱离固定圆柱）时的角速度的问题。现在原问题1次规约为计算质心的加速度（子问题），2次规约为质心的加速度表达式（子问题的子问题），3次规约为判断质心的轨迹（子问题的子问题的子问题），4次规约为计算圆轮的角速度（子问题的子问题的子问题的子问题）。

解决原问题的思路如下：

首先运用动能定理计算出圆轮在任意位置（不脱离圆柱）时的角速度，对圆轮的角速度求一阶导数计算出圆轮的角加速度;

其次根据式（1）和（2），计算出质心的切向和法向加速度;

最后运用质心运动定理计算出题目中的所求的切向约束力（静摩擦力）和法向约束力，问题即可解决。

3 结语

根据问题规约法，采用逆向思维的方式，找出学生解决问题的最近距离（子问题与子问题之间的问题距离），求解刚体动力学普遍定理的综合应用问题，不失为一个好的方法，该法不仅可以锻炼学生的逆向思维，而且还拓宽了学生解决问题的思路，同时在解决问题的过程中学生也学会了如何学习。

2015年山东省属本科高校教学改革研究项目“基于国家级特色专业的车辆工程应用型人才培养”;2. 山东省精品课程建设经费资助项目（2012（15））;3. 山东理工大学课程综合改革项目（2015-115074）

参考文献

[1] 哈尔滨工业大学理论力学教研组.理论力学[M].北京：高等教育出版社，1996.

[2] 王颖.维果茨基最近发展区理论及其应用研究[J].山东社会科学，2013（12）：180-183.

[3] 孙颖，王芳，杨英英.“最近发展区”理论对工程教育的启示[J].高等工程教育，2012（6）：96-97.

[4] 蔡自兴等.人工智能及其应用[M].北京：清华大学出版社，1996.