常识上见规律 活动中出实效

◎张昀

一、背景分析

《数学课程标准》（2011版）指出，课程内容的选择要贴近学生实际，有利于学生体验与理解、思考与探索.课程内容的组织要重视过程，处理好过程与结果的关系；要重视直观，处理好直观与抽象的关系；要重视直接经验，处理好直接经验与间接经验的关系.人教版教材中，安排了部分数学活动的内容，在实际教学中，现状往往不尽人意，有的只停留在教师做，学生看的状态中；有的只是作为了解内容，让学生自学；甚至有的对这部分内容置之不理.2017年10月，在学校组织的骨干教师课堂教学展示活动中，我上了一节数学活动课——《月历中的规律》，引起了听课老师的强烈反响，也得到了他们的充分肯定.下面就我在本节课中设计的活动进行详细阐述.

二、案例描述

1.活动一

师：同学们，下面是2017年5月的月历，请思考下面两个问题，看看会得出什么规律？

①如图1，每一横排相邻两个数字之间有什么关系？

规律1：____________________________________________.

②如图1，每一竖列相邻两个数字之间有什么关系？

规律2：____________________________________________.

生1：每一横排相邻两个数字之间差为1.

生2：每一竖列相邻两个数字之间差为7.

设计意图：从与生活密切相关的月历入手，让学生通过观察得出横排相邻两个数字以及竖列相邻两个数字的关系.数学来源于生活，又服务于生活，让学生养成用数学的眼光看世界的习惯.

2.活动二

师：同学们，下面是2017年4月的月历，请认真思考，逐一解决下面五个问题.

如图2，任意框出竖列上三个相邻的数.

①设较小的数为x，则其它两个数分别为____________.

②设较大的数为x，则其它两个数分别为____________.

③设中间的数为x，则其它两个数分别为____________.

④若三个数之和为69，则这三个数分别为____________.

⑤三个数之和可能为72吗？为什么？

生3：设较小的数为x，则其它两个数分别为x+7，x+14.

生4：设较大的数为x，则其它两个数分别为x-7，x-14.

生5：设中间的数为x，则其它两个数分别为x+7，x-7.

生6：若三个数之和为69，则这三个数分别为16，23，30.

师：谁能说出你的解题方法和步骤.

生7：设中间的数为x，则其它两个数分别为x+7，x-7.

根据题意，得 x+x+7+x-7＝69，

解得 x＝23.

所以 x+7＝30，x-7＝16.

师：你对问题⑤是怎样理解的？

生8：若三个数之和为72，则这三个数分别为17，24，31.而2017年4月没有31号，因此，三个数之和不可能为72.

设计意图 用字母表示数是整式一章学习的重要内容之一，从不同的角度设出未知数，根据活动一得出的结论，就可以表示出另外的两个数，这样做的目的就是增强学生的符号意识.问题④的解决方法可以是算数方法，也可以是用方程思想解决，体现了解决问题方法的多样性.问题⑤虽然可以算出数值，但与实际不符，说明数学应用型问题得出的数值要经得起实际的考量，也就是说检验的步骤不可缺少.

3.活动三

师：同学们，下面是2017年5月的月历，所提出的两个问题的规律有何关系？

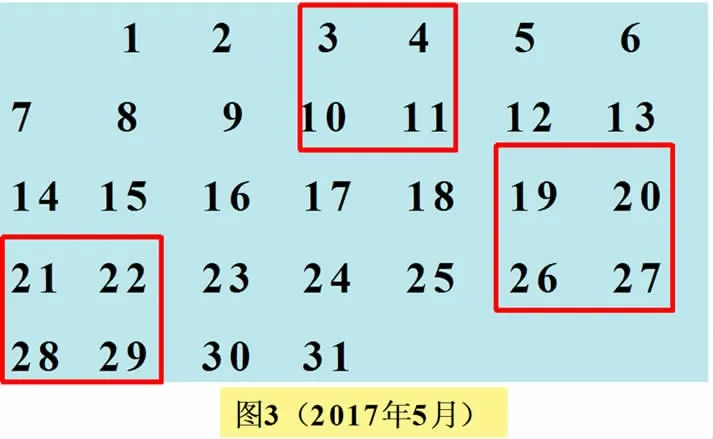
①如图3，红色方框中4个数之间有什么关系？

规律3：__________________________________________.

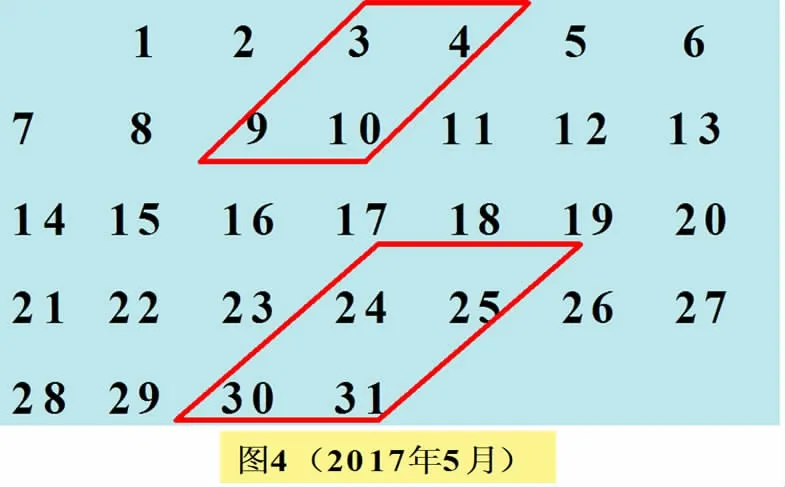
②如图4，红色平行四边形框中4个数之间又有什么关系？

规律4：___________________________________________.

生9：方框中的4个数，对角线上两个数的和相等.

生10：平行四边形框中的4个数，对角线上两个数的和相等.

生11：上述两个规律的共同之处是：对角线上两个数的和相等.

设计意图 由红色方框中4个数变化为红色平行四边形框中的4个数，条件发生变化，图形由特殊到一般，但其中不变的是对角线上两个数的和相等.用恰当合理的变式营造一种生动活泼、宽松自由的氛围，有利于学生掌握基础知识，有益于培养学生的应变能力.有意识地引导学生从“变”的现象中发现“不变”的本质，从“不变”的本质中探求“变”的规律，使知识点融会贯通，逐步培养学生灵活多变的思维品质，增强其应变能力，激发其学习数学的积极性和主动性，提高其数学素质，培养其探索精神和创新意识，从而真正把对能力的培养落到实处，切实增强数学课堂教学的有效性，使数学课堂教学得以升华.

4.活动四

师：同学们，下面是2017年5月的月历，你能解决下面的四个问题吗？

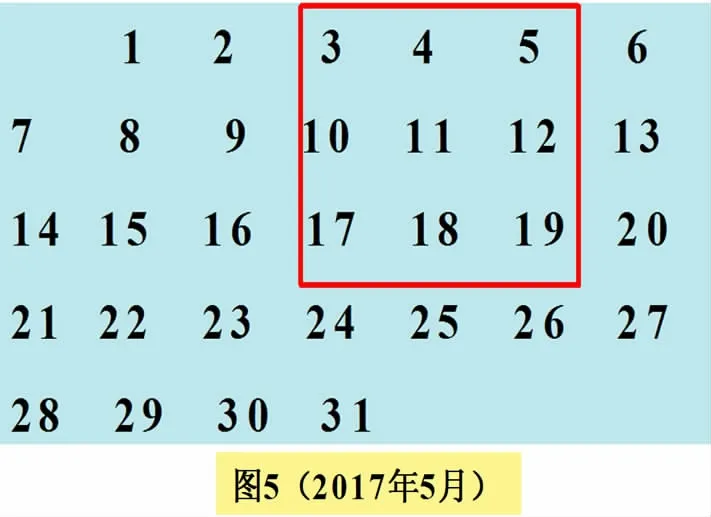
①如图5，红色方框中9个数的和与方框中心的数有什么关系？

规律5：__________________________________________.

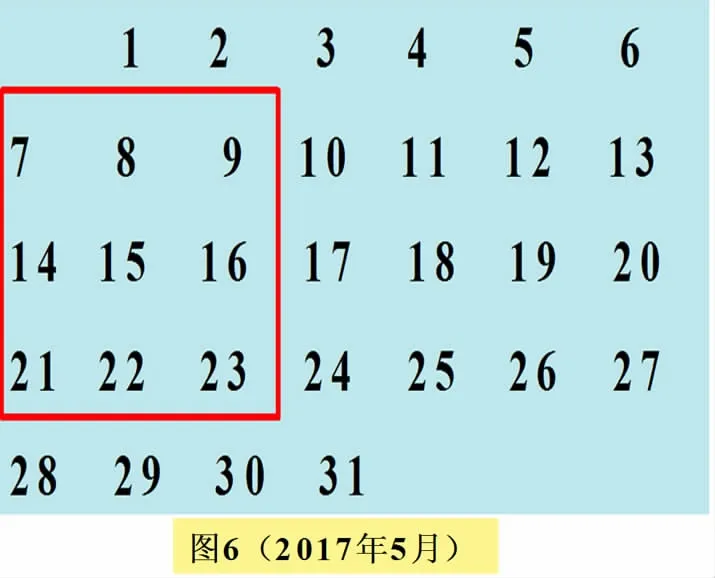
②如果将红色方框移至图6的位置，①中的关系还成立吗？

③不改变方框的大小，将方框移动几个位置试一试，你能得出什么结论？你能证明这个结论吗？

④这个结论对于任何一个月的月历都成立吗？

生12：方框中9个数的和等于方框中心的数的9倍.

生13：如果将红色方框移至图6的位置，①中的关系仍成立.

生14：不改变方框的大小，将方框移动几个位置，得出的结论是：方框中9个数的和等于方框中心的数的9倍.

师：同学们，你们是如何证明这个结论的呢？

生15：设方框中心的数为x.

则 x+（x+1）+（x-1）+（x+6）+（x-6）+（x+7）+（x-7）+（x+8）+（x-8）＝9x.

∴方框中9个数的和等于方框中心的数的9倍.

生16：这个结论对于任何一个月的月历都成立.

设计意图 红色方框中由4个数变化为9个数，先由具体的数探讨规律，用不完全归纳法得出结论.再用字母表示数，通过演绎推理的方式验证结论.通过本活动培养学生数学抽象、逻辑推理等核心素养.

5.活动五

师：同学们，下面是一长方形数阵，以小组讨论解决下列问题.

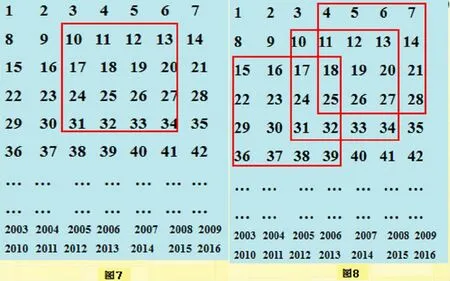
现将连续自然数1至2016按图7的方式排成一个长方形阵列，用一个方框框出16个数.

①图7中框出的这16个数的和是__________.

②图8中，用正方形任意框出16个数，若设最小的数为x，则这16个数的和可表示为___________（用含x的式子表示）.

③图7中，能否使一个正方形框出的16个数之和分别等于2010，2016？若不能，试说明理由；若能，请求出该正方形框出的16个数中的最小数和最大数.

规律：__________________________________________.

生17：图7中框出的这16个数的和是352.

生18：图8中，用正方形任意框出16个数，若设最小的数为x，则这16个数的和可表示为16x+192.

师：同学们，你能详细说出问题③的思考过程吗？

生19：由题意，得16x+192＝2010，

由题意，得16x+192＝2016，

解得x＝114.

所以x+24＝114+24＝138.

所以，不能使一个正方形框出的16个数之和等于2010.能使一个正方形框出的16个数之和等于2016，此时，最小数为114，最大数为138.

设计意图：由月历拓展为数阵，是数学活动的升华.学生已有月历中规律探索的经验，通过类比，自然可以明确数阵中存在的规律，从而达到解决问题的目的.一方面培养学生的应用意识，另一方面培养学生思维的灵活性.

三、教学反思

《数学课程标准》（2011版）指出，数学教学活动是师生积极参与、交往互动、共同发展的过程.本节活动课，学生在老师不断抛出的问题的驱动下，带着问题去实践，从而寻找规律，得出答案，这是一种探索知识，完善自身的过程.本节课活动容量较大，设计了五个活动，由简单到复杂，对学生的思维以及课堂时间的掌控有一些挑战.通过数学活动，我对活动课的设计和效果有新的理解.

1.数学活动要体现参与性 建构主义认为，学习不应该被看成是对教师所授予知识的被动接受，而是学习者以自身已有的知识和经验为基础主动参与活动，即学生能积极主动地学习.在数学活动课中，通过教师学案设计，由浅入深，逐级引导，从简单的问题解决中尽可能的让所有学生都能参与，随着活动的深入，探索问题的热情逐步被点燃，全体学生参与的效果明显显现.

2.数学活动要体现趣味性 数学活动课虽然不像音乐课悦耳动听，不像语文课故事引人入胜，但数学活动课在看似平常的数字、图案中，教师能设计好找规律的步骤，通过学生个体和小组集体合作，一个规律接着一个规律被同学们发现，心中的喜悦自不必说，也能增强大家的集体荣誉感和责任心，共同完成任务，也懂得了分工协作才能得胜利的道理.

3.数学活动要体现实效性 虽然活动课往往自由讨论，气氛热烈，看起来比较活跃，但一定要注重活动的实效性.一是活动课不能单单活动有声有色，忘记了学生掌握知识、提高能力的初心；二是不能老师不注重活动过程的引导，活动偏离中心或者活动不够深入，全体学生参与度不高，这些都不能很好地提高活动课的实效.