基于ABAQUS的油气缓冲器静压曲线摩擦力超差分析及排除

吴龙飞，宋 燕，罗愿欣

（中航飞机股份有限公司长沙起落架分公司，陕西 汉中723000）

0 引言

某型主起落架缓冲器在制造过程中，需要进行静压曲线试验，其摩擦力经常超出设计要求。对于起落架缓冲器而言，摩擦力过大可能会造成起落架在着陆过程中发生卡滞，缓冲器密封组件在使用过程中承受过大载荷，加剧密封组件的磨损，最终导致过早失效；摩擦力过小容易产生缓冲器密封泄漏，造成缓冲性能失效，引发事故[1]。因此，研究静压曲线绘制机理，建立合理的数学模型和动力学模型，分析影响静压曲线摩擦力的因素，以便采取相应的措施提高缓冲器静压曲线试验合格率具有重要的意义。

1 静压曲线试验机理

缓冲器是一个由外筒、活塞杆及密封部位三个主要部分构成的密闭容器，内部充填有液压油与高压氮气[2]。使用时，将外筒固定，活塞杆承受飞机载荷受压缩入，密闭腔体积变小，液压油腔也随之变小，部分液压油在压缩力挤压下，通过节流缝隙，摩擦发热吸收能量，与引同时，腔内气体随着体积变小，压力上升，储存能量。为验证缓冲器的储量性能，在缓冲器制造时，可以通过绘制静压曲线来检查。

其过程描述如下：将外筒进行固定，通过试验机向活塞杆施加压缩力，在施力过程中保持活塞杆以不大于40 mm/s的速度压入（如图1），在此过程中，同时测量活塞杆的位移和力，并以位移为横轴，力为纵轴，建立瞬时点的曲线，即为静压曲线。如图2所示。

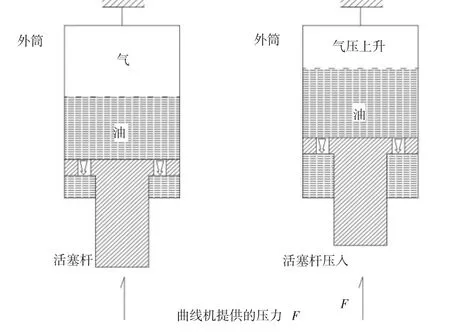
图1 静压曲线绘制机理

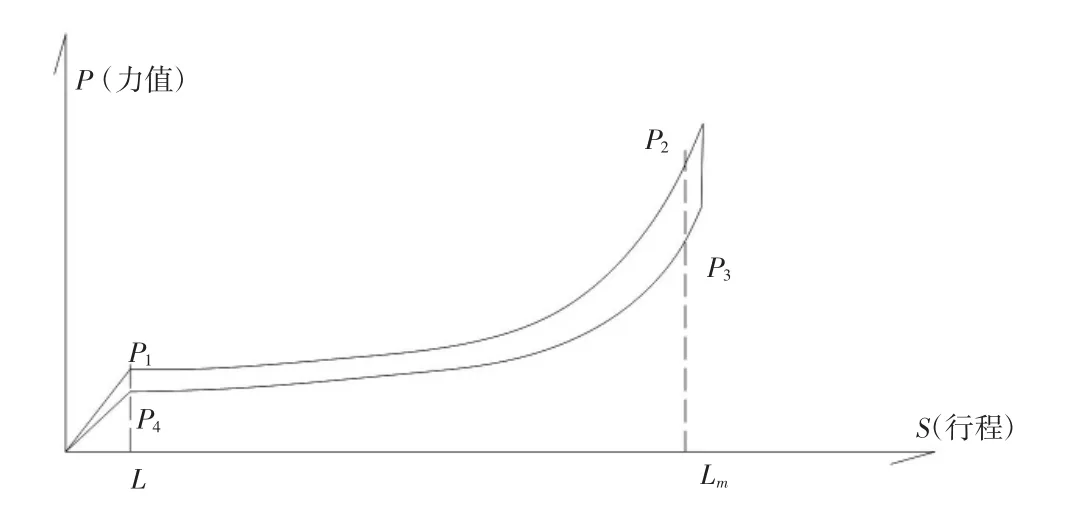
图2 静压曲线图

静压曲线中摩擦力的来源分析：取活塞杆作为受力分析对象，可知其受到向下的气压力F，曲线试验机施加的向上力P，活塞杆与外筒配合面之间的滑动摩擦力f（见图3）。

图3 活塞杆受力分析

结合静压曲线图与活塞杆受力分析可知，图中P1、P2、P3、P4为曲线试验机顶升力，在曲线上任意行程位置，可以从曲线图上取得两个顶升力，而对缓冲器而言，活塞杆行程一定的情况下，腔内体积是一定的，故腔内气压也是一定的，所以有：

可以看出，当 P1、P2确定后，P3、P4的值是由产品的摩擦力决定的。

2 缓冲器静压曲线试验摩擦力的来源分析

以某型号缓冲器为例，其主要结构如图4，主要由外筒、活塞杆、分油节流结构、密封结构等部分组成。在缓冲器静压曲线试验过程中，活塞杆受压缩入的摩擦力来源是活塞杆支撑环与外筒、胶圈－滑环密封组与外筒、支撑轴套与外筒、大螺母与活塞杆。

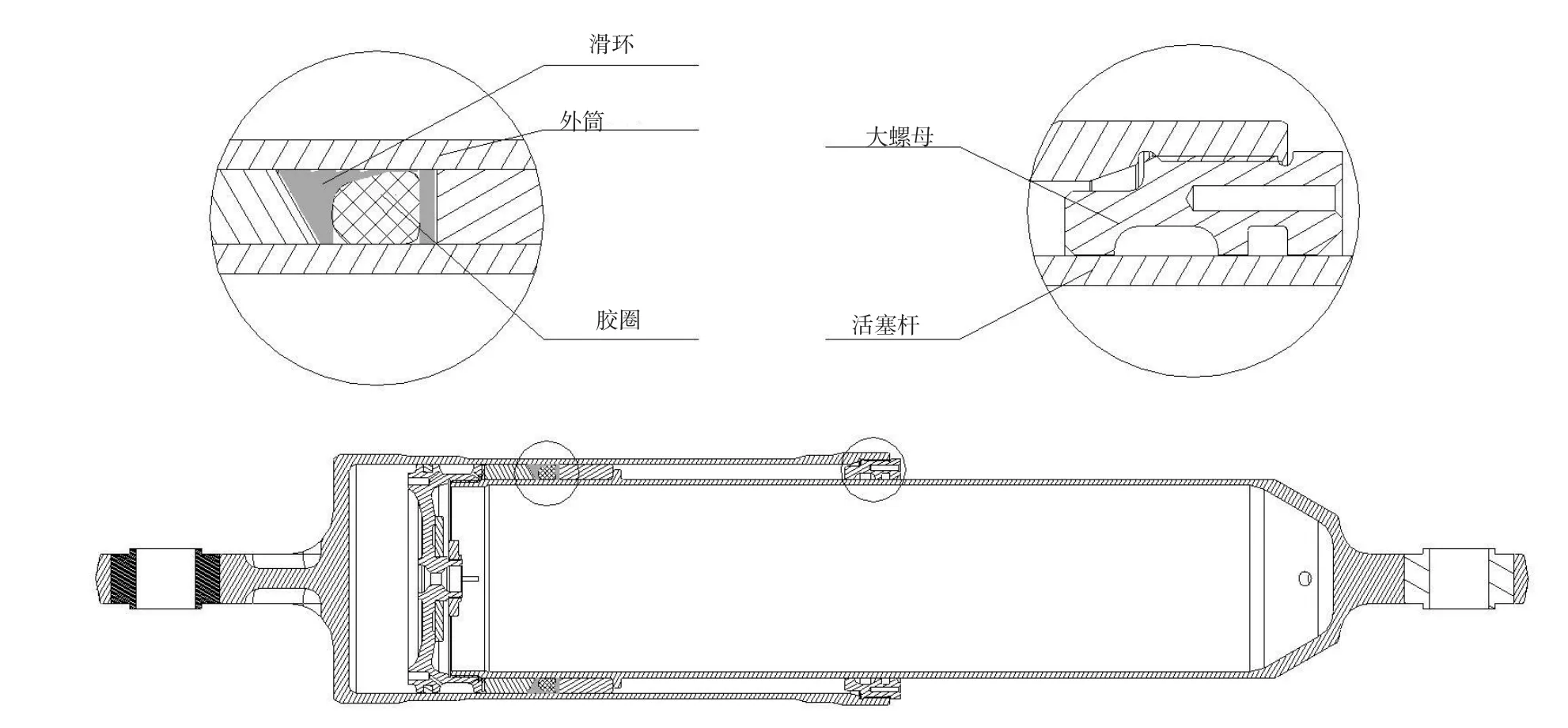
图4 缓冲器摩擦副的构成

对于活塞杆支撑环与外筒之间的摩擦，因为支撑环为开口节流功用，故存在较大浮动间隙，摩擦力可以忽略。胶圈－滑环密封组为弹性压力元件，需要其起挤压密封作用，在缓冲器受压过程中会承受高压气体挤压力，因此是分析的主要对象之一。支撑轴套与外筒之间配合，主要为导向作用，配合性质为间隙配合，外筒受压扩张后，两者接触力很小，所以摩擦力可以忽略；大螺母与活塞杆的配合，从结构尺寸上看为间隙密封，但为防止活塞杆外露表面附着物进入缓冲器内部，在两者之间设置有防尘圈，有一定的摩擦力，且缓冲器受压后，活塞杆外径有扩张趋势，会使配合间隙减少甚至相互挤压，产生硬接触，所以也是分析的对象之一。综上所述，静压曲线中摩擦力超差主要是由于两个摩擦副摩擦力之和超差影响的，要知道摩擦力的情况就必须对这两个摩擦副进行分析。

3 有限元模型的建立与仿真

3.1 胶圈－滑环密封组结构及材料特性分析

以某缓冲器为例，其密封组的结构如图5，主要由起弹性支撑和密封作用的O形圈，起滑动摩擦与密封作用的滑环构成。

图5 胶圈滑环密封组

在活塞杆受压运动时，胶圈滑环密封组固定在活塞想杆上，与外筒产生相对运动，形成摩擦。

由式f＝μN可知，需要计算滑环作用在外筒上的正压力，实际上也就是计算胶圈施加在滑环上的径向压力。

缓冲器中的胶圈材料为试5 171，邵氏硬度为77±5，属于超弹性、近似不可压缩材料[3]，其应力应变关系非常复杂，国内外学者已提出了许多用于描述橡胶材料应力应变关系的应变能函数形式。目前采用较为广泛的穆尼－茹夫林Mooney-Rivlin模型，其应变能函数为：

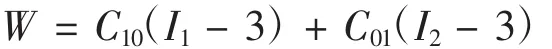
式中，W为应变能密度；C10、C01为材料Mooney常数；I1、I2为第一、第二应变张量不变量[4]。

考虑到要对超弹性材料进行有限元分析，需要软件在非线性领域具有强大的功能，因此选择了ABAQUS有限元分析软件，它可以进行复杂的接触分析、材料非线性分析，多步骤分析[5-6]。其使用较为简便，建立模型非常快捷，只需要用户提供结构的几何形状、边界条件、材料性质、载荷情况等工程数据，选择合适的单元划分，软件即可在分析计算过程中自动选择合适的收敛准则，从而保证其结果的精确性。

3.2 胶圈－滑环密封组有限元模型建立

从胶圈－环滑密封组与活塞杆结构可知，两者均为轴对称圆环结构，其中活塞杆和滑环因其弹性模量比胶圈大得多，故可视为刚体。在ABAQUS中输入各结构的截面尺寸，即可建立平面轴对称几何模型，也可通过使用扫掠三维模型，由平面对称几何模型生成三维图（如图6），在分析过程中只需要在平面模型下进行即可。

胶圈采用ABAQUS自带的穆尼－茹夫林Mooney-Rivlin模型，材料模型参数C10、C01的确定参照文献[1]，C10=1.051，C01=0.263，压缩比 D1=1.2E-4（近似不可压缩），网格划分采用CAX4H单元类型，布种密度0.1。在本模型中，存在滑环与胶圈、胶圈与活塞杆两处接触对，对于接触问题的定义，本文采用罚单元法。罚单元法是指在两接触面的各节点间建立一种伪单元来模拟面与面的接触[7-10]。此类单元具有2个自由度，可在节点的X和Y方向上移动，用于模拟胶圈与滑环、活塞杆之间的接触变化情况。摩擦模型采用库仑模型，摩擦系数按0.23。

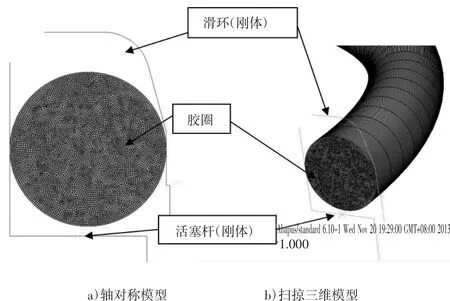
图6 结构图

3.3 建立胶圈-滑环密封组的边界条件和加载方式

根据胶圈-滑环密封组装配过程和试验过程中密封组的受压情况，首先约束活塞杆的所有自由度，再利用滑环刚体的强制位移，来模拟胶圈的安装过程，使胶圈处于安装到位的压缩状态，最后在胶圈的上侧逐步施加油压载荷使胶圈处于受压状态，来模拟密封组的受压过程。

考虑到胶圈非线性大位移接触问题的复杂性，通常先定义一个只有很小位移的载荷分析步，让设定的接触对平稳地建立接触关系；第二步再施加真实的位移，减少模型计算时收敛的困难，节省计算时间，在前两个载荷步计算结果的基础上；第三步是在胶圈未与活塞杆及滑环接触的表面施加与边界垂直的压强载荷，模拟单侧油压的作用，从而达到模拟装配和试验过程的密封受力变化。

3.4 仿真及数据分析

以某产品缓冲器为例，活塞杆外圆直径取φ200 f7，外筒内孔直径取φ230H7，胶圈内圈直径取φ170，截面直径φ17.5±0.3，胶圈槽宽尺寸在18.66～17.66 mm采用调整垫方式进行确定。缓冲器充气压力为5 MPa，静压曲线在10 mm处与196 mm处的平均力值分别为 P2＝（1 148 ± 30）kN；P3＝（1 009 ±30）kN；摩擦力在两个行程处要求不大于15 kN，100 kN；胶圈以设计要求最小直径φ17.1浸泡后，溶胀按0～10%（GJB250A）为计算依据，胶圈直径变化范围取为φ17.1～φ17.8；调整垫圈厚度增加量按0.1、0.2、0.5、1对胶圈进行压缩情况控制（槽宽理论值18.66 mm）；数据模拟静压曲线在10 mm处与196 mm处（对应的缓冲器内部压力5.44 MPa、25.97 MPa），取不同胶圈直径、不同调整垫片厚度，观察滑环上正压力（RF）变化情况，如图7。

图7 不同油压下胶圈密封压强平面云图与三维扫掠图

从图8中可以看出，当胶圈直径取φ17.1 mm时，调整垫厚度在0～1 mm范围内变化，对于缓冲器压力在5.44 MPa下，曲线摩擦力几乎没有受到影响；当胶圈直径增大到φ17.3时，调整垫厚度增加达到0.5 mm左右，对于缓冲器压力在5.44 MPa下的曲线摩擦力影响就开始比较明显，且继续增加达到0.7 mm左右，摩擦力将超出设计要求的最大值15 kN；当胶圈直径增大到φ17.5时，调整垫厚度对摩擦力增加有明显效果，在调整垫增加厚度达到0.4 mm左右，摩擦力将超出设计要求的最大值15 kN，所以，如果只考虑胶圈密封结构对摩擦力的影响，要确保缓冲器压力在5.44 MPa下不超差，应选择胶圈直径范围为φ17.1～φ17.5较为理想。

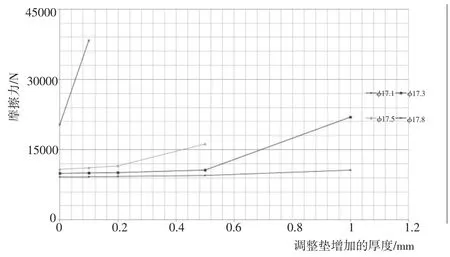
图8 压力为5.44MPa时，胶圈直径、调整垫增加厚度及摩擦力的关系图

从图9可以看出，随着胶圈直径的增大及调整垫厚度的变厚，密封组摩擦力也随之增大。从定量上看，其最小的摩擦力值是36.1 kN（胶圈直径φ17.1，不增加调整垫厚度），如果不考虑活塞杆与大螺母的摩擦力，将会出现在压缩行程196 mm处的曲线摩擦力低于设计要求值（摩擦力要求范围39.5 kN～99.5 kN），但图中也可以看出最大的摩擦力51.7 kN仍未超出设计要求的在压缩行程196 mm处的曲线摩擦力范围（39.5 kN～99.5 kN）。所以考虑活塞杆与大螺母之间的摩擦副对静压曲线摩擦力有影响是正确的。

图9 压力为25.97MPa时，胶圈直径、调整垫增加厚度及摩擦力的关系图（不考虑活塞杆与大螺母摩擦力）

3.5 活塞杆－大螺母的有限元模型建立

从产品结构上看，活塞杆与大螺母均为回转体，故分析模型为轴对称圆环结构。在本次分析当中，活塞杆、大螺母强度相当，视为可变形柔性体，外筒在此摩擦副中不直接参与摩擦，可视为刚体。故建立如如图10、图11所示平面轴对称几何模型。

在某产品选材中，活塞杆材料为300 M超高强度钢，大螺母为铜材料，查询相关材料手册，可知300 M超高强度钢弹性模量为210E6，泊松比取0.3，铜材料弹性模量103E6，泊松比取0.3。

模型网格划分采用CAX4R单元类型，布种密度1。在模拟分析过程当中，只存在活塞杆与大螺母的接触对，摩擦模型采用库仑模型，摩擦系数按0.1。

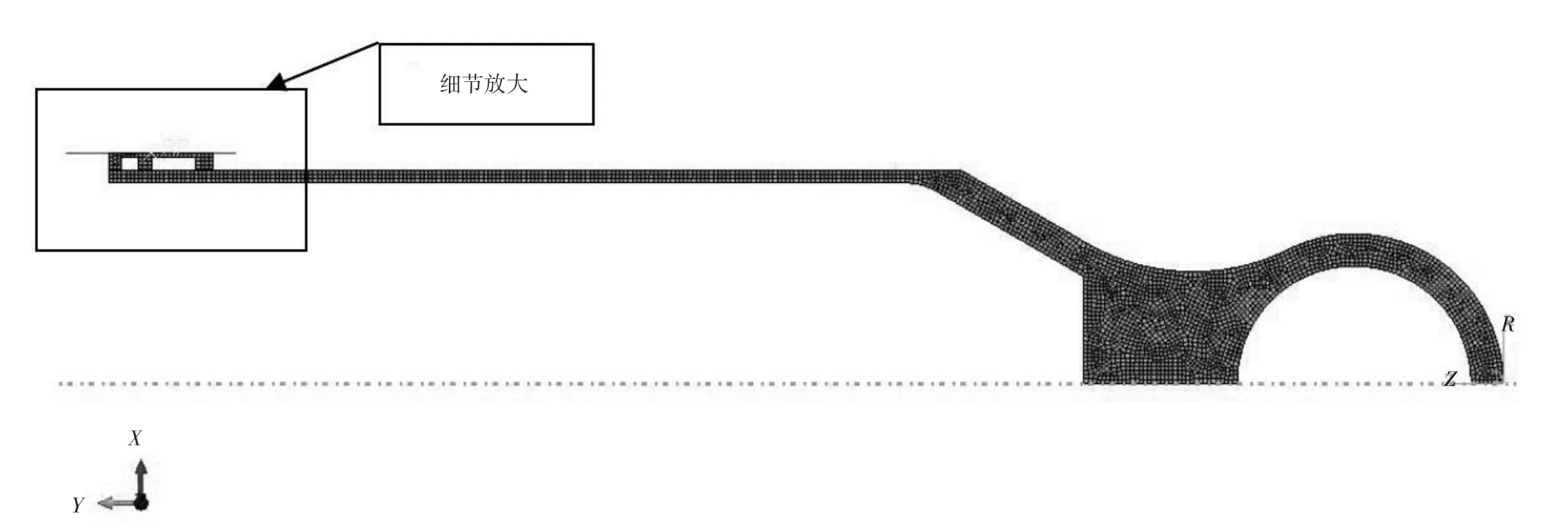
图10 大螺母与活塞杆的有限元模型

图11 大螺母与活塞杆的有限元模型（细节部分）

3.6 接触对的边界条件及加载分析

根据产品的受力情况，首先约束活塞杆固定孔与外筒刚体的所有自由度，然后在活塞杆的内腔施加油压载荷，使其达到静压曲线绘制过程中的工作状态，观察活塞杆与大螺母的间隙及正压力情况。

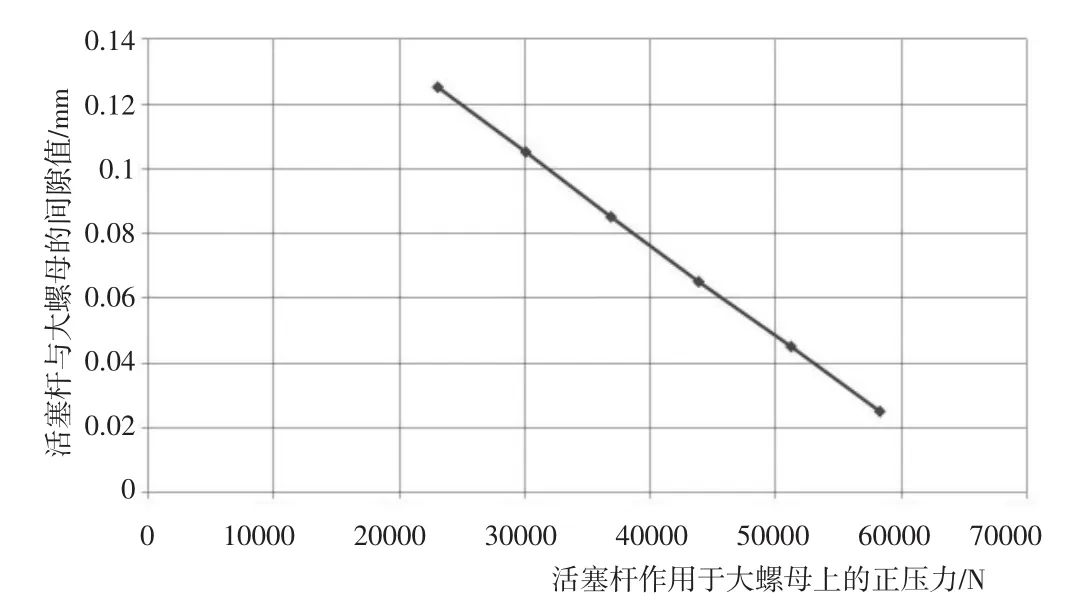
图12 间隙与活塞杆作用在压紧螺帽上的正压力关系图

3.7 缓冲器曲线摩擦力综合分析

基于以上两个摩擦副的仿真分析结论，依据摩擦力与配合间隙、胶圈直径、调整垫厚度以及油压的关系图，对数据进行拟合，则可得出静压曲线试验过程中，摩擦力与压力、压缩量、配合间隙等的相互关系图（见图 12～16）。

（1）当活塞杆与大螺母之间润滑良好时，摩擦系数按0.1，有如下规律（见图13）：

图13 胶圈直径、调整垫增加的厚度及摩擦力关系图（润滑良好）

（2）在活塞杆与大螺母间隙为0.025（设计要求最小间隙值）时，胶圈直径尺寸在φ17.1情况下，调整垫厚度增加值不大于1 mm，曲线摩擦力不会出现超差；胶圈直径尺寸在φ17.3情况下，调整垫厚度增加值不得大于0.7 mm，否则曲线摩擦力会出现超差；胶圈直径尺寸在φ17.5情况下，调整垫厚度增加值不得大于0.4 mm，否则曲线摩擦力会出现超差；胶圈直径尺寸在φ17.8情况下，曲线摩擦力必然会出现超差，如图14所示。

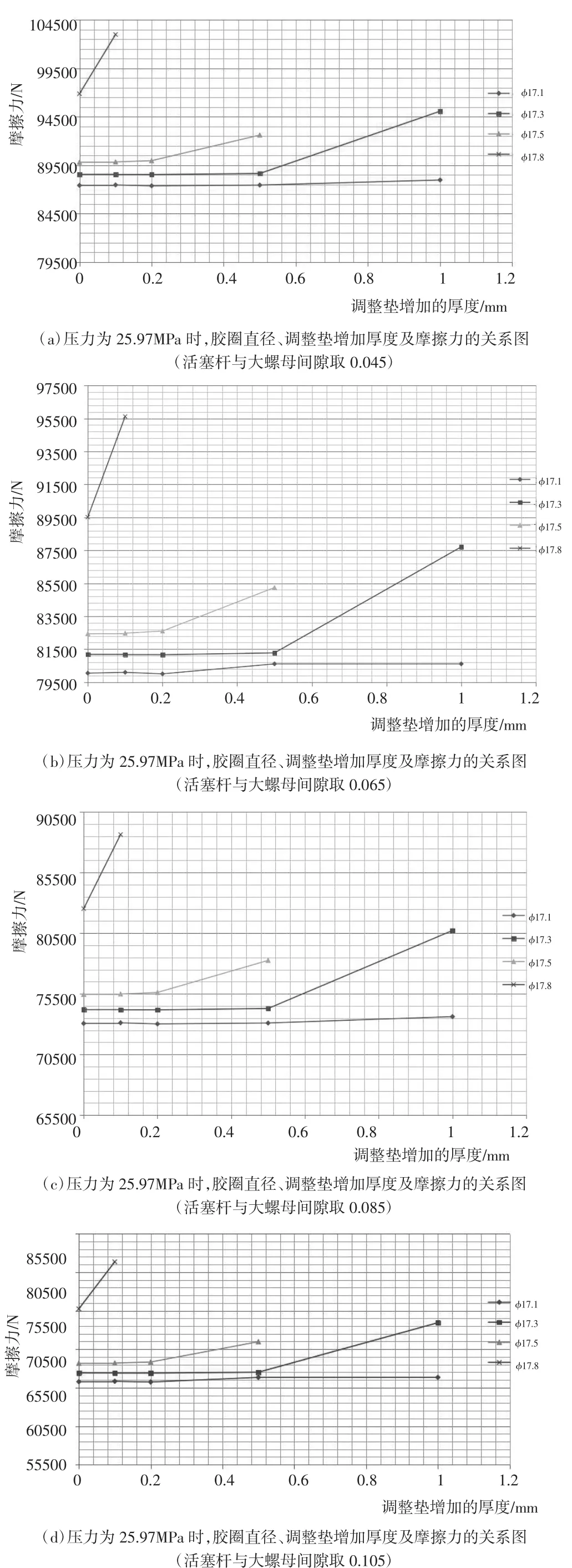
图14 胶圈直径、调整垫增加的厚度及摩擦力关系图（润滑良好）

（3）在活塞杆与大螺母间隙为0.045～0.105 mm时，胶圈直径尺寸在φ17.1情况下，调整垫厚度增加值不大于1 mm，曲线摩擦力不会出现超差；胶圈直径尺寸在φ17.3情况下，调整垫厚度增加值不得大于0.7 mm，否则曲线摩擦力会出现超差；胶圈直径尺寸在φ17.5情况下，调整垫厚度增加值不得大于0.4 mm，否则曲线摩擦力会出现超差；胶圈直径尺寸在φ17.8情况下，曲线摩擦力必然会出现超差。

（4）当活塞杆与大螺母之间润滑情况较差时，容易产生干摩擦，摩擦系数取0.15时，有如下规律（如图 15）：

图15 胶圈直径、调整垫增加的厚度及摩擦力关系图（润滑不良）

（5）在活塞杆与大螺母间隙为0.025～0.065时，无论胶圈直径尺寸在φ17.1～φ17.8之间如何变动，曲线摩擦力必然会大于设计允许的最大摩擦力，如图16所示。

图16 胶圈直径、调整垫增加的厚度及摩擦力关系图（润滑不良）

（6）在活塞杆与大螺母间隙为0.085～0.105 mm时，从图中可以看出，曲线摩擦力基本处于合格范围内。那么从上述的分析结果可以得知，此间隙区间内曲线摩擦力能否合格的关键在于低压状态下调整垫的厚度选择。

4 控制措施

综合以上分析结果，可以得出以下控制要求：

（1）为保证曲线摩擦力处于设计要求的范围内，装配前，应当对活塞杆与大螺母的间隙、胶圈截面直径进行测量。

（2）根据胶圈的截面直径，选择合适的调整垫满足槽宽要求，然后综合导向部分的配合间隙，再进行装配和静压曲线试验。

（3）当导向部分间隙在0.025～0.15 mm范围内变化时，通过改善其摩擦面之间的润滑条件，对降低静压曲线摩擦力有一定作用，且随着间隙的变大，降低摩擦力效果愈差。

5 结论

通过利用软件仿真分析得出的控制措施，经实际应用，该型油气缓冲器静压曲线试验摩擦力超差情况大幅降低，验证了该仿真模型的可行性，并对其它橡胶类密封结构的密封压力及摩擦力分析有一定的借鉴意义。