一种具有自适应动量因子的BP神经网络算法实现∗

杨文龙 肖程望

（武汉邮电科学研究院 武汉 430074）

1 引言

电子商务行业的飞速发展也是大数据时代到来征兆之一，消费者在茫茫商品海洋中很容易就被淹没了，大数据时代也同样遇到这样的问题。诚然，这也将是机遇。如何有效地利用用户的浏览记录、购买记录和评价数据等相关信息，推荐用户可能需要或感兴趣的商品，以节省用户的宝贵时间，是目前解决信息过载、提高电商竞争能力的有效途径。这一问题被推荐算法［1］有效地解决了，尤其是协同过滤推荐算法在这一领域中的卓越表现，更是大大提高了推荐效率和精确度。因此，推荐系统在领域中发挥的重要作用将愈发明显。

推荐系统在这样的大数据时代的背景下发挥了巨大的作用，用户面对海量的信息做到有针对性地选取自己需要的东西变得异常艰难，供应商确切地推送用户真正需要、真正感兴趣的东西也很困难。推荐系统的出现成了这一棘手问题的救命稻草。它通过挖掘用户的历史行为，对用户的兴趣范围进行建模，并通过该模型对用户未来的行为进行预测，从而建立了用户和内容的关系［2］。当前较为热门的推荐方法包括:基于内容的推荐、协同过滤［3］的推荐、基于关联规则的推荐推荐、基于效用的、基于知识的推荐方法和组合推荐等。本文研讨的是关于协同过滤推荐算法的改进。

2 系统算法原理简介

2.1 协同推荐算法简介

本文主要说的是使用神经网络算法做协同过滤。协同过滤推荐算法是推荐系统的关键，它主要包括基于用户、基于物品及基于模型的。基于用户的协同过滤［4］主要是着眼于用户之间的相似度，根据相似用户喜欢的物品相互推荐，推荐给目标用户后形成列表供目标用户选择。基于物品的协同过滤是把着眼点放在物品之间联系上，根据用户的历史记录，获取历史记录物品的特性和评分，找到相似属性的物品，根据用户历史记录的物品属性，形成物品推荐列表供用户选择［5］。基于模型的协同过滤是对以上两种方式的结合，形成一个用户偏好模型，根据用户历史记录或者用户个人资料建立一个模型，通过机器学习算法完成模型的构建［6］。

2.2 BP神经网络模型［7］简介

BP算法的基本思想大致归纳如下:算法的学习过程分为输入信号的正向传导和误差信号的反向传导。在数据信号的正向传导阶段，通过各隐含层逐层加权计算，训练数据样品数据从输入层传入传递到输出层。到达输出层后，系统计算结果与数据集实际数据（矫正信号）相比较，结果不符，则将误差反向沿着正向传播阶段逐层输入。在误差反传这一过程，将误差信号分解到所有神经单元中，在将误差信号反转分解传输的过程中，其作为依据修正各隐层神经单元的连接权值，以期达到期望的结果。就这样信号向前传播，误差被传播回来，并且调整每个层的权重，周而复始。直到将权重调整到可接受的误差范围或满足预先设定的要求。这样周而复始的权值调整过程就是其学习的经过［8］。如图1所示。

图1 BP神经网络基本结构

3 BP神经网络改进及系统设计

3.1 BP神经网络的不足

标准BP算法虽在诸多方面很有优势，但是在实际应用中仍然存在不足。BP神经网络的非线性优化容易产生部分极小点问题，对网络造成负面影响［9～10］。另外，在调整权重时，由于它没有考虑到时间t前的梯度方向，只是按t梯度误差的时间降方向进行调整，从而使训练过程中的权值调整发生振荡，收敛速度较慢。为解决该问题引入了动量因子改进算法，该方法有效地缓解了权值调整时导致的收敛震荡问题。

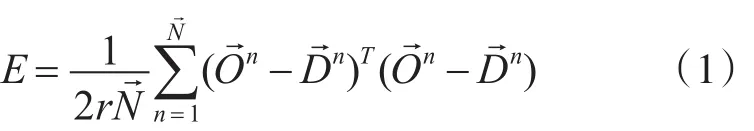
但是，当误差平面出现陡峭下降紧跟着陡峭上升的深坑时，网络训练可能会跳过或者停留在底部，不能实时根据当前的误差数据适应走势。动量因子如果取值过小，那么加入动量项的作用就大打折扣；若动量项的值太过靠近1，会导致算法不稳定。故选择合适的动量因子很重要［11］。

3.2 BP神经网络模型改进方案

r表示输出节点数，含动量因子的BP算法的权值更新表示式（2）为

其中η表示学习率；α为动量因子。

自适应动量因子BP算法的权值更新公式（3）为

其中，∇E(k)为E关于w在w=w(k)处的梯度，第k次训练网络得到的网络权值向量是w(k)，k=1，2，…E为误差。λ为自适应动量项的初始值，本实验中选择λ=0.01。

以上是动量因子改进算法的数学表达式。在传统的权值更新中，动量项都是一个常量，这样在算法误差曲面平坦的时候不能快速通过，在误差曲面陡峭的部分会出现算法的不稳定。误差曲面的陡峭程度可以用误差关于权值向量的梯度来表示。当梯度值较大时，误差变化较快，误差梯度陡；当梯度值较小时，误差变化较慢，误差梯度平缓。基于上面的问题，自适应动量因子可以轻松解决，∇E(k)为E关于w在w=w(k)处的梯度，这样动量因子e-λ-||∇E(k)||就会实时更新，根据当前需要灵活改变。此时，在误差平面的平坦部分，动量因子增大，使权值更新向量增大，较快地通过平坦区；在误差陡峭部分，动量因子减小，权值更新向量减小，避免出现算法不稳定现象。综上可知，自适应动量因子法可以使网络训练加速收敛。图2是改进算法的代码实现。

图2 改进算法的代码实现

本算法的大致组成是根据相似性计算目标用户的TOP-N相似用户；选择前N个用户的项目评分数据组成项目-评分矩阵，建立用户评分预测模型；根据项目-评分矩阵训练网络；输入待评分项目预测评分；最后比对预测分与实际评分通过MAE值评测算法性能。用改进的BP神经网络对协同推荐算法进行改进［12］，其详细算法流程如图3。

具体的BP算法的编程实现步骤如下:

1）网络初始化；

网络初始化的内容包括:权值矩阵W、V，误差E，学习率η及网络训练后的精度Emin；

2）输出训练样本对，计算各层输出；

3）计算网络输出误差；

4）计算各层误差信号；

5）调整各层权值；

6）检查网络总误差是否达到精度要求；

若网络总误差达到精度要求，则训练结束；否则跳转2）。

4 实验分析

4.1 数据采集和BP网络设计

本文的数据是采用的Movielens数据集，它主要用于将协作、过滤和关联规则结合起来向它们的用户推荐电影［13］。所使用的数据有100000条评价数据是1682部电影由943个用户评价所得。该数据集的五分之四用于训练网络，剩下的五分之一用于做测试。电影中有18个属性，所以BP网络的输入层和隐藏层是18个节点，输出层是1个节点。其中输入层的18个节点分别代表评分项目的18个属性值，隐含层节点数与输入层节点数对应；输出层的节点代表目标项目的预测评分值。

4.2 实验环境介绍

使用工具箱newff（）实验生成网络、train（）训练网络及sim（）方法模拟。基于改进的BP网络算法模型的训练结果［14］如图4。

图4 BP算法改进前后训练比较图

从图4可以看出两点:一方面是网络模型的稳定性有了大幅的提高，看训练结果的走势图，改进前的抖动幅度很大，而改进后的基本都一直在平滑的下降；另一方面，在稳定性的基础上大大减少了网络训练的时间，改进后的训练大概在700次的时候就趋于稳定不变了，而改进前的到达设定的1400次还没有趋于稳定。同时，也在一定的情况下提升了预测结果的准确率。整体看来，自适应动量因子方法很好地解决了网络模型的稳定性问题，并且大大减少了模型的训练时间以及提高了结果的有效性。

4.3 推荐结果度量标准

推荐系统的评价标准可分为三类:预测精度测量、分类精度测量和等级精度测量。平均绝对偏差MAE（Mean Absolute Error）是预测精度度量方法中比较常用的，我们采用它作为度量的标准［15］。预测的用户评分和实际的用户评分之间的绝对偏差是通过MAE计算得到的，伴随着MAE的减小推荐质量变高。式（4）如下:

（p1，p2，…，pN）表示由网络预测的用户评分集合，（q1，q2，…，qN）表示对应的实际的用户评分，N表示参与测评的用户的个数。实验结果如图5所示。

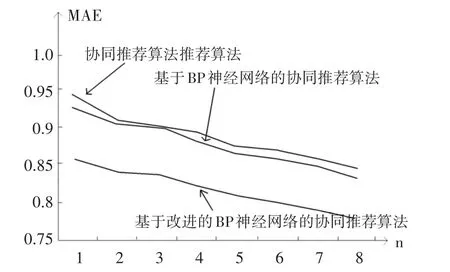
图5 不同算法的推荐结果比较

由图5统计结果比较可以看出，基于传统BP神经网络的推荐系统比直接使用协同推荐算法的MAE值小，但是相对于使用自适应动量因子的BP神经网络的推荐算法，改进后的算法在推荐质量上得到了明显的改善。因此改进算法的有效性得到证明。

5 结语

随着近几年互联网的爆炸式发展，网络数据也是海量出现，这使得我们在面对这种海量数据时感觉到无从下手。因此，各种推荐系统的应用就应运而生了。本文提出了一种新的确定BP算法动量因子的方法。这种方法是一种自适应的，它能够在每次迭代的过程中根据权值空间中的误差曲面的陡缓自动的改变动量因子的大小。经过实验仿真可以看出，自适应动量因子比常动量因子在稳定性及训练时间方面都有大幅的提升，同时也在一定情况下提升了网络的预测准确性。