多特征融合与尺度自适应核相关滤波跟踪算法∗

冯 汉 王永雄 张孙杰

（上海理工大学光电信息与计算机工程学院 上海 200093）

1 引言

近几年相关滤波（Correlation Filter，CF）在目标跟踪领域取得很大的进展。David S Bolme等率先提出了误差最小平方和滤波器（Minimum Output Sum of Squared Error，MOSSE）［1］，首次将相关滤波用在目标跟踪上，极大提高了跟踪速度。João F.Henriques等通过引入循环移位矩阵和核技巧（Circulant Structure of Tracking-by-Detection with Kernel，CSK）［2］可以在基本不损失计算速度的基础上极大地扩充训练样本，在后续工作中提出了核相关滤波器（High-Speed Tracking with Kernelized Correlation Filters，KCF）［3］，在 CSK 的基础上利用 Pedro等提出的快速梯度直方图特征（Fast Histogram of Oriented Gradient，FHOG）［4］提高跟踪精度。Martin Danelljan［5］等在 Van De Weijer提出的颜色属性特征（Color Name，CN）［6］基础上提出颜色自适应的思想，选取最有鉴别力的颜色特征进行跟踪。针对目标前后运动造成的尺度变化问题，M Danelljan等首次提出了平移滤波加尺度滤波的思想（Discriminatiive Scale Space Tracker，DSST）［8］，两个滤波器单独训练、局部优化，能精确估计目标尺度。深度学习在目标跟踪领域也取得越来越重的地位，Valmadre［15］等结合相关滤波和end-to-end方式在CNN中训练，能达到很好的跟踪效果。

为了提高跟踪算法的鲁棒性，本文在传统KCF的框架上融合了FHOG特征和CN特征作为平移滤波器获取目标的平移位置，并利用PCA获得最有鉴别力特征，实现颜色自适应以减少计算时间。同时采用平移滤波加尺度滤波的思想，增加一个33尺度的尺度滤波器精确估计目标的尺度变化。在标准数据集［17］进行了对比实验，实验数据表明本文算法与近几年经典的跟踪算法比较，在外观变形、尺度变化、光照变化、背景相似干扰等情况下平均性能均优于对比方法，且能满足实时性。

2 基于核相关滤波的平移滤波器

2.1 核相关平移滤波器模型

传统核相关滤波跟踪模型的建立是通过求解期望输出与实际输出响应的最小均方误差，找出合适的滤波器w。假设一共有n个训练样本响应函数 f(z)=wTz，期望输出与实际响应输出的最小均方误差如式（1）所示:

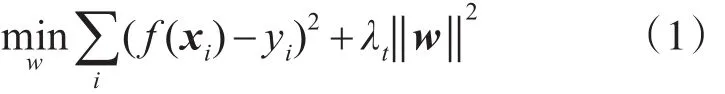
式（1）λt为正则项系数，防止过拟合。式（1）中滤波器w的解为

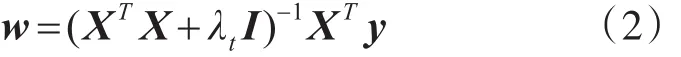
式（2）I为单位矩阵，上标T代表转置操作。式（2）求逆操作需要很大，利用复频域的相关性质能减少求逆计算量，式（2）在复频域的表达式为

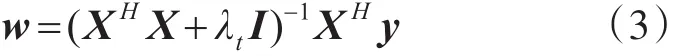
XH为 X的Hermitian变换即 XH=(X*)T，X*为 X的复共轭，在实数域式（2）和式（3）等价。

2.2 循环移位及频域优化

通过循环移位操作可以极大增加训练样本集，提高滤波器的鲁棒性，类似于信号的基波与谐波，通过投影到复频域并利用相关性质［10］可以进行快速求解。循环移位矩阵在傅里叶空间对角化的形式如下:

式（4）V为循环移位矩阵，v为基向量，F是傅里叶变换矩阵，上标∧代表傅里叶变换，上标H代表共轭装置。如果训练样本X由基样本x循环移位生成，则结合式（3）和式（4）求得:

式（5）∧运算符代表傅里叶变换，⊙运算符代表点乘，*运算符代表复共轭。

2.3 核技巧及模板更新

式（5）给出了线性可分情况下的解析解，定义核函数κ将输入x映射到高维空间φ(x)可以解决线性不可分情况，滤波器w可以用φ(x)的线性组表示。此时响应函数 f(z)=wTz在高维空间的表达形式为核函κ 的表达形式为 κ(x，x′)= φ(x)，φ(x′) ，， 为点乘运算符，所以响应函数 f(z)的核变换形式为

通过式（6）求得式（1）的核形式解为

式（7）K 为 n×n的核矩阵，表达式为 Kij=κ(xi，xj)，当K是一个循环移位矩阵时结合式（4）可得式（7）快速解形式为

式（8）∧运算符代表傅里叶变换，kxx′表示为核矩阵K的第一行。

通过定义Kz为训练样本x和候选区域z的核相关循环移位矩阵，Kxz为Kz的第一行，式（6）可以表示为 f(z)=(Kz)Ta，结合式（4）可得输出响应为

式（9）∧运算符代表傅里叶变换，⊙运算符代表点乘。为了减少计算量本文采用如下更新策略:

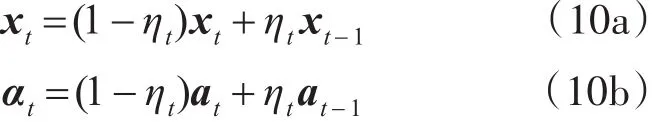
式（10）xt为当前第t帧训练样本，xt-1为上一帧第t-1帧训练样本，at为当前帧权重系数，at-1为上一帧权重系数数，ηt为模板更新速率。

3 多特征融合与降维

传统的KCF算法利用FHOG特征能较好地体现目标轮廓信息。由于目标在运动过程中容易发生形变和部分遮挡等情况，在严重情况下如果只用FHOG特征容易跟丢目标，由于颜色特征对于上述情况有较好的适应性，所以本文融合FHOG特征和CN特征，CN特征通过把RGB特征映射为黑、蓝、棕、灰、绿、橙、粉、紫、白、红和黄共11种属性，使颜色特征更具有区分度。融合31维FHOG特征和11维CN特征会增加计算量，导致跟踪速度降低。为了达到更好的实时性，本文利用文献［5］提出颜色自适应的思想，把11维CN特征降为2维，自动选择最显著的两维CN特征，在不损失特征重要信息的基础上提高跟踪速度。通过最小化损失函数获得合适的维度降低映射以获取最有鉴别力的颜色特征，该损失函数的形式如下:

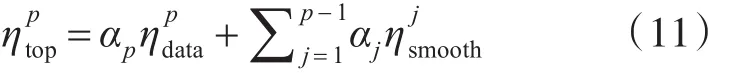
式（12）xp为当前帧特征，Bp是由标准正交向量组成的D1×D2维投影矩阵，分别代表当前帧特征维数和降维后的维数。为第 j帧的平滑项，定义如下:

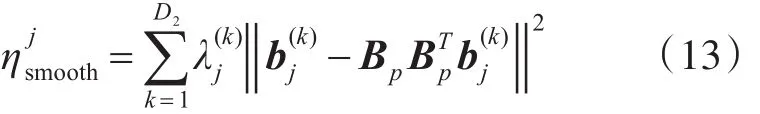
j对应的特征值。通过数据项（12）和平滑项（13）可知损失函数（11）只有在BP=I时才能最小化。Bp由矩阵特征值分解（EVD）得到的前D2个最大特征值对应特征向量组成，Cp为 xp的协方差矩阵，Λj为D1×D2维的对角矩阵，其值由λ(jk)组成。

上式推导得到一个合适的投影矩阵Bp，通过线性映射 xp(m，n)=BpTxp(m，n)，∀m，n 就可以得到新的D2维特征图。

4 尺度自适应滤波器

通过前两节计算得到了一个融合多特征的平移滤波器，能够很好解决目标跟踪过程中的外观变形、部分遮挡等情况。但是在实际运动过程中，目标相对相机的前后运动会造成尺度较大幅度的变化，如果滤波器模板尺度不变就会导致该滤波器不能学习到合适比例的前景和背景信息从而导致跟踪效果不佳。

针对以上问题，本文利用平移加尺度滤波的思想，单独训练一个33尺度的一维滤波器，采用局部优化，单独训练的方式使得该滤波器更加灵活。

4.1 尺度滤波器模型

尺度滤波器模型的建立通过最小化尺度滤波器h与训练样本 f的相关运算结果，然后计算与期望输出g之间的最小均方误差，最后计算出最优的尺度滤波器h，如下式所示:

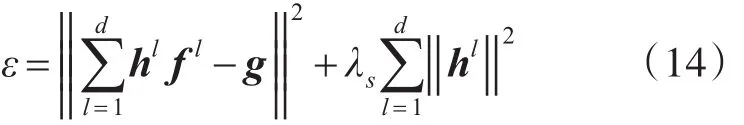
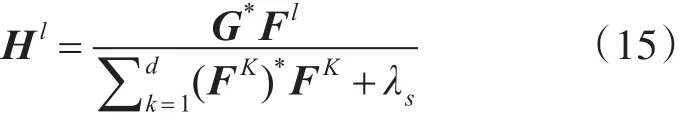
式（15）大写字母代表式（14）中其对应小写字母对应的傅里叶变换，*为复共轭运算符。为了减少计算量通过模板更新策略获取近似的滤波模板:

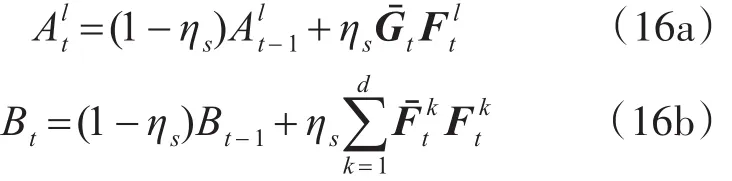
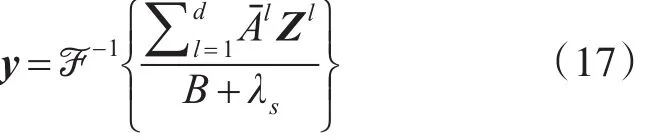
式（17）中Z为当前帧目标区域z的傅里叶变换，上标l代表第l维特征图，ℱ-1运算符代表傅里叶逆变换。

4.2 尺度输出

式（18）给出了一维尺度滤波器的响应输出表达式，通过计算 y最大值所在的位置n，，S为尺度总个数。则当前帧目标尺度为anP×anR，a代表尺度因子，P×R表示前一帧目标的宽和高。由于尺度系数an是指数函数为非线性函数，即可实现对较大目标进行粗略检测，对较小目标进行细致检测的效果。

5 实验结果与分析

为了有效评估本文算法的性能，选取了近几年经典的四种算法做对比试验，包括代表经典相关滤波的CSK算法；以FHOG特征为代表的KCF算法；以颜色特征为代表的CN算法；以尺度变换为代表的DSST算法。本实验采用的数据集为VOT2014数据集，该数据集共有50段视频序列，包含了尺度变化、背景相似干扰、快速运动、运动模糊、光照变化等常见的跟踪干扰问题，能够比较全面反映算法性能。同时为了兼顾每个算法的独特性质，所以选取的视频序列最大限度保证对每个算法的公平性。

5.1 实验环境及参数设置

本实验的硬件平台为Inter（R）Core（TM）i7 2.90GHz处理器，8GB内存，软件平台为Matlab R2015a。本文二维高斯形状输出和二维高斯核函数以及一维高斯形状输出的标准差σ=0.5。FHOG特征细胞大小为4，梯度直方图方向个数为9。第一节正则化系数λt=0.0001，模板更新速率ηt=0.02，第三节正则化系数λs=0.01，模板更新速率ηs=0.025。第三节尺度因子α=1.02，尺度数量S=33。第二节期望输出y选用二维高斯形状输出，核函数κ选用二维高斯核函数。

本实验采用视觉跟踪中最常用的三种评估方法来评估各算法性能:中心位置误差法（Center Location Error，CLE），距离精度法（Distance Precision，DP）和重叠精度法（Overlap Precision，OP）。CLE评价方法即计算目标预测位置(xp，yp)和真实位置(xr，yr)的平均欧式距离N为样本的帧数。DP评价方法即计算CLE数据中小于一定阈值的帧数占总帧数的百分比，本实验取该阈值为20像素。OP评价方法即计算目标预测位置及大小与实际位置及大小的重叠率大于一定阈值的帧数占总帧数的百分比，该阈值一般选取PASCAL［14］的评价标准为0.5。

5.2 定性分析

为了直观各算法性能差异，选取了实验集中6类具有代表性的视频序列做定性分析。每个视频序列特性如表1所示，同时展示其中3个视频序列每个序列的3帧图片显示各算法跟踪结果，实验结果如图1所示，图1不同颜色框代表不同算法的跟踪结果。

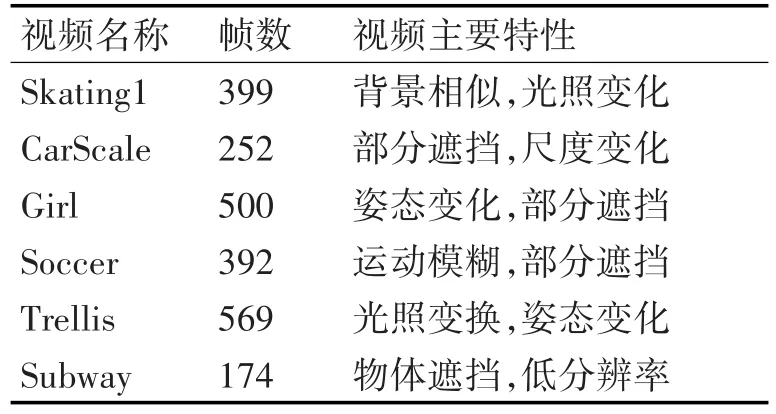
表1 视频特性

图1 定性分析图

5.3 定量分析

通过5.2节定性分析，能直观对比本文算法与对比算法结果，接下来通过定量分析观察各个算法之间性能差异。表2数据给出了表1视频序列中的CLE、DP和OP在20个像素阈值下的数据。表中加粗部分为最优数据，通过观察各性能指标的均值参数可知本文算法在三个性能指标上均取得最优效果，CLE，DP，OP值分别为 7.38/像素，95.53%和85.5。

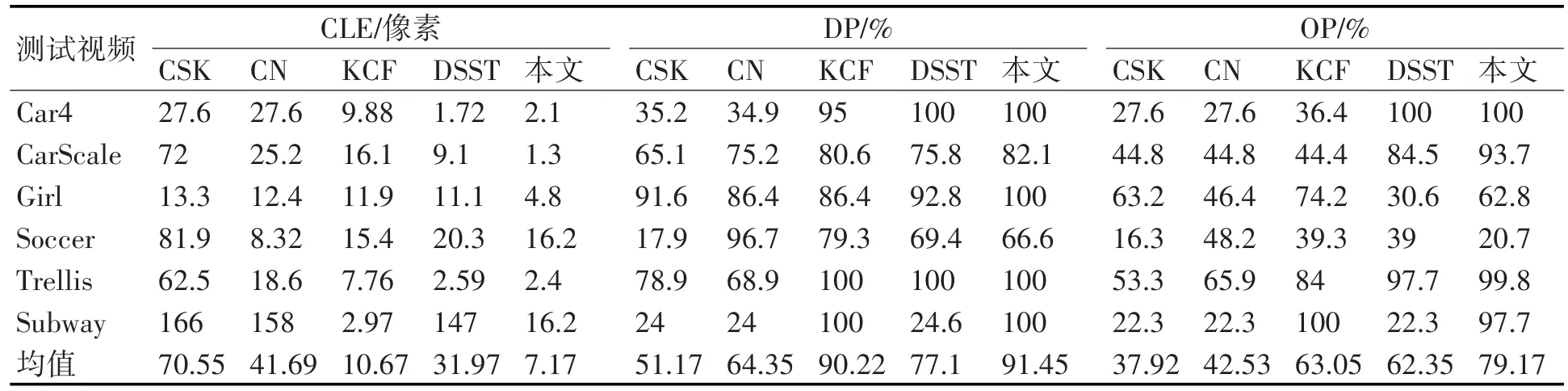
表2 定量分析

5.4 全面对比

为了直观显示各算法综合性能，前两节只提取了6个典型特性视频序列做对比分析。为了不失客观性，实验选取符合各算法特性共26个视频序列作全面对比实验。同样采用5.1节提到的三种性能指标评估算法性能。由于对比视频序列较多，如果仅用均值指标来评估各算法性能会受到极端数值影响，所以增加中值指标来反映各算法的性能差异，可以避免极端数值的影响。具体数据如表3、表4所示。从表3、表4数据可以看出本文算法性能和对比算法比较能取得较好效果。

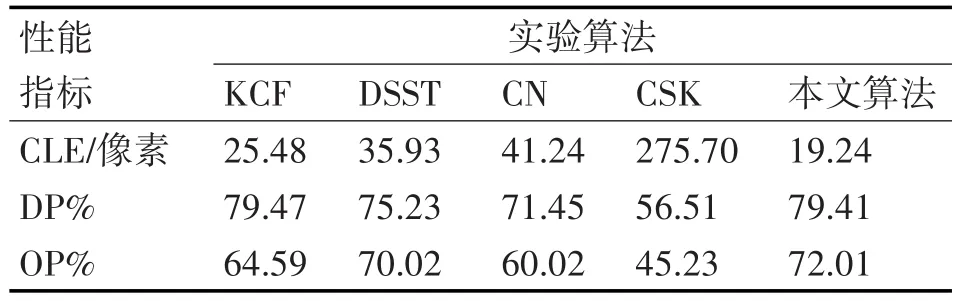
表3 均值指标

表4 中指指标

5.5 速度对比

上几小节主要分析各算法跟踪精度，可知本文算法的跟踪精度是最高的。接下来实验对比各算法跟踪速度，实验得出表1所示6个视频序列跟踪速度，并取它们的平均值作为最终跟踪速度，具体数据如表5所示。从表5数据可知本文算法跟踪速度达到29fps，可以满足跟踪的实时性。

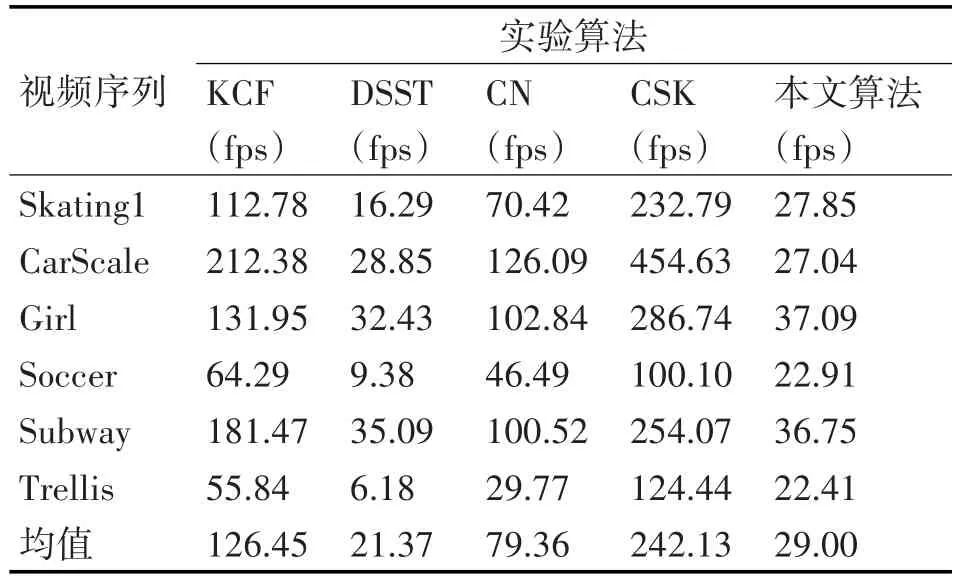
表5 跟踪速度

6 结语

本文提出的多特征融合与尺度滤波器算法，在传统KCF算法基础上，融合了FHOG特征和降维后的CN特征，能更加全面地反映目标信息。同时借鉴了DSST算法提出的尺度划分思想单独训练一个33尺度滤波器，在取得目标平移位置后，通过尺度滤波器来精确估计目标的尺度大小。通过对比试验可以看出本文算法平均性能均优于对比算法。虽然本文算法与对比算法比较能取得较好跟踪效果，但是在引入多特征和尺度滤波器的时候同时也降低了跟踪速度。由于本文算法并未改进模板更新策略，所以在针对目标大幅度形变，大面积遮挡和快速运动模糊的情况下同对比算法一样跟踪结果仍然不尽人意，还需要大量的研究工作完善该算法。