基于混合人工蜂群的模糊聚类算法∗
2019-06-01姚雅高尚
姚雅 高尚
(江苏科技大学计算机科学与工程学院 镇江 212000)
1 引言
由于聚类(clustering)可以作为获取数据的分布状况的工具,并在此基础上进一步地分析,聚类(clustering)分析已经成为数据挖掘的主要任务。聚类就是把不同数据对象集合划分成不同组群的过程,即把数据对象分成多个类或簇,同一聚类中的数据相似度高而不同聚类中的数据相似性低[1]。聚类算法已经广泛应用在诸如市场分析、Web文档、信息安全、金融等很多方面。然而,在现实生活中,有些问题拥有严格的划分界限,有些问题并没有严格的界限划分,具有模糊性。因此,针对这类聚类问题,人们提出了用模糊的方法进行处理。由Dunn[2]和 Bezdek[3]提出的模糊 C-均值聚类算法(FCM),就是一种被普遍应用的基于目标函数的模糊聚类算法。该算法简单、快速,具有比较直观的几何意义,但同时也存在着对初始值条件与噪声数据敏感,容易使目标函数陷入局部最优的缺点。
近年来,为了取得更为理想的聚类效果,已经产生许多对FCM算法的改进算法,如文献[4]将点对约束与FCM算法结合,文献[5]将属性权重区间监督运用到FCM算法中,文献[6]提出一种新的选取聚类中心的方法对FCM算法进行了改进。现如今又掀起了一股新的将智能优化算法与聚类算法相结合的研究潮流,将粒子群算法(particle swarm optimization,PSO)[7]、蚁群算法( ant-colony algorithm)[8]和遗传算法(genetic algorithm,GA)[9]等与聚类算法结合的文献中聚类结果的稳定性和准确性已经得到了较大的提高。人工蜂群(artificial bee colony,ABC)算法是 2005 年由 Karaboga[10]建立的一种新型的模仿蜂群采蜜行为的群智能优化算法,并引起了广泛的关注,如今在群智能领域已经掀起了新的研究热潮。文献[6]中将其与粒子群优化算法、遗传算法和差分进化算法(differential evolution,DE)这三种算法进行对比,通过ABC算法得到的结果相对较好。因此,本文将其与FCM算法相结合,得到的新的聚类算法能够有效地提高聚类结果的稳定性和准确性。然而,ABC算法也存在局部搜索能力较差、易于过早陷入局部最优点等缺点。分布估计算法(Eestimation of Distribution Algorithm,EDA)[11]是一种基于概率模型的具有良好全局探索能力的新型进化算法。UMDAc是一种变量无关的分布估计算法的典型代表,它是UMDA算法的扩展,并且它描述连续解空间的概率模型时是采用了高斯分布。文献[12]对2011年关于分布算法做了总结,文献[13]对连续域多变量耦合问题进行了分析,还有许多学者也在分布估计算法方面做出了出色的成果。本文将人工蜂群算法与UMDAc算法相结合,提出了不同的蜜源生成策略,得到一种基于分布估计的人工蜂群算法。然后将改进后的混合人工蜂群算法与FCM算法结合,使得聚类效果得到显著提高。
2 人工蜂群算法及其改进研究
2.1 基本人工蜂群算法
在人工蜂群(ABC)算法[14]中,主要由蜜源、被雇佣的蜜蜂和未被雇佣的蜜蜂三个基本部分组成。其中,蜜源是指可采得花蜜的地点,在算法中其价值由适应度值来表示;被雇佣的蜜蜂是指已经发现蜜源的蜜蜂,也称其为引领蜂;未被雇佣的蜜蜂是指未找到蜜源的蜜蜂,主要负责寻找和开采蜜源,根据分工的不同分为两种:侦察蜂和跟随蜂。该模型定义了蜜蜂拥有三种最基本的行为模式:当引领蜂找到丰富蜜源时,就会招募其他的蜜蜂跟随到此处进行采蜜;当蜜源的花蜜变得较少时,则放弃该蜜源,与该蜜源相关的引领蜂也随即变成了侦察蜂;侦察蜂随机寻找一个新蜜源并进行开采,随即就变成引领蜂执行任务。ABC算法的实现过程如下:
1)初始化阶段。初始化循环的最大次数MCN,蜜源被废弃的条件参数limit,随机生成SN个初始解(SN 即为跟随蜂的个数或引领蜂的个数),其中是一个 d 维的向量,并依照式(1)对其进行初始化蜜源i的位置。
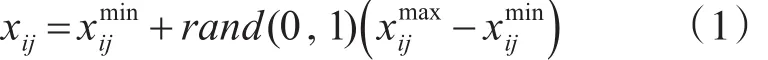
每个蜜源的位置相当于一个优化问题的可行解,其“收益率”对应于可行解的适应度值 fit(xi),可依据式(2)进行计算:
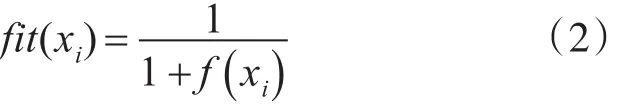
式中:f(xi)是人工蜂群算法的目标函数值。
2)引领蜂行为阶段。在此阶段,引领蜂利用“贪婪选择”法则,将旧蜜源和通过邻域搜索获得的新蜜源的适应度值进行比较,当新蜜源优于旧蜜源时,则用其替换掉旧蜜源,否则仍然保持不变。在进行邻域搜索时,根据下式由旧蜜源xi产生新蜜源vi。
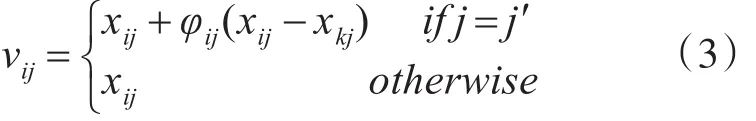
3)跟随蜂行为阶段。当引领蜂完成任务返回蜂巢时,它们会通过跳摇摆舞将把蜜源信息传递给跟随蜂。跟随蜂根据获得的蜜源信息通过轮盘赌方式选择自己将要开采的蜜源。收益率越高的蜜源吸引到的跟随蜂就越多。在ABC算法中,跟随蜂依据概率值决定蜜源,因此蜜源xi被跟随蜂选择的概率为
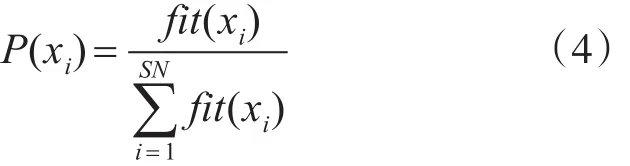
当跟随蜂选择好一个蜜源进行开采时,它也依据式(3)进行邻域搜索,并同样采用贪婪原则进行选择。
4)侦察蜂行为阶段。当某蜜源的收益率连续limit次仍没有被更新时,则表明该蜜源已经陷入局部最优,此时应当放弃该蜜源,与此同时,引领蜂转换变为侦察蜂,并根据式(1)产生一个随机的新蜜源。
2.2 基于连续分布估计的人工蜂群算法
1)算法原理
分布估计算法是一种基于概率模型的新型的进化算法,它是将遗传算法和统计学习相结合,依照当前种群的概率模型来引导产生下一代种群,该算法是对生物进化“宏观”层面上的建模,具有良好的全局探索能力。
分布估计算法在编码方式上可以分成两种:离散型编码和连续型编码,孙增圻和周树德的论文《分布估计算法综述》[15]对离散型编码的分布估计算法进行了详细的阐述。PBILc和UMDAc分别是由PBIL和UMDA算法扩展而得的变量无关的连续分布估计算法的典型代表。而现在对人工蜂群(ABC)算法的研究主要是针对连续人工蜂群算法[16~17]的,因此为了提高人工蜂群算法的全局探索能力,本文将人工蜂群算法与连续分布估计算法UMDAc相结合,提出一种基于连续分布估计的人工蜂群(Univariate Marginal Distribution Continuation-artificial Bee Colony,UMDAc-ABC)算法,主要是通过改进人工蜂群(ABC)算法的新蜜源生成公式,利用优质蜜源的概率分布来引导产生新蜜源,使得算法在收敛速度、鲁棒性等方面得到明显的改善。而关于二进制人工分群算法的研究,可以参考文献[18]提出了一种易于实现的差分演化二进制人工蜂群算法,文献[19]提出了一种基于分布估计的二进制人工蜂群算法。
其中,UMDAc的过程是:每一代都由概率向量P(x)随机产生M个个体,计算出这些个体的适应度值,然后从中选出N个最优个体,并用这N个个体更新概率向量P(x)(N ≤M ) 。其中,用Pq(x)表示第q代概率向量,即表示选择出的最优的N个个体,其中服从高斯分布,估计如下:
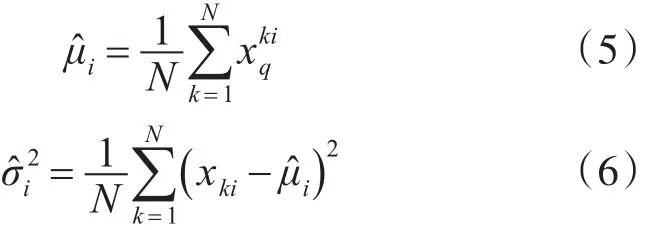
因此,引领蜂在进行邻域搜索时蜜源的更新公式变为式(7)。
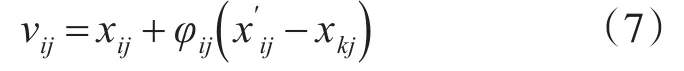
2)具体实现步骤
UMDAc-ABC算法的具体实现步骤如下所示。
(1)初始化。对SN、MCN和limit三个变量进行初始化,利用式(1)初始化蜜源其满足在解空间中依据均匀分布随机生成,同时根据式(2)计算每个蜜源对应的适应度值。
(2)执行如下的循环:
①选择适应度值比较高的SN 2个个体,计算出它们的均值和方差:和
diag( )σ1,σ2,…σd;
②引领蜂阶段,由上面计算出的均值和方差可以得到一个多元正态分布利用上面改进的邻域搜索方式,即根据式(7)产生一个新蜜源vi,并采用贪婪原则判断是否需要替换旧蜜源xi;
③类似步骤①,重新选择SN 2个优质蜜源,计算出他们的均值和方差;
④跟随蜂阶段,即跟随蜂根据(1)中获得的蜜源的适应度值,利用式(4)计算每个蜜源被选中的概率,通过轮盘赌方式选择自己将要开采的蜜源;根据改进的邻域搜索方式再次产生新的蜜源,并利用贪婪原则在新蜜源与原来引领蜂对应的旧蜜源之间进行判断是否需要替换;
⑤重复步骤③;
⑥侦察蜂阶段,即判断是否有蜜源已经陷入局部最优,如果有则放弃该蜜源,同时与之对应的引领蜂转换为侦察蜂,并利用式(1)开始探寻下一个新蜜源并进行采蜜,进而又由侦察蜂转换成引领蜂;
⑦记录当前的最优蜜源,检查是否满足终止条件,如果满足则输出最优蜜源(解);否则则继续进行循环。
3 基于混合人工蜂群的模糊C-均值聚类算法
3.1 模糊C-均值聚类算法
模糊C-均值聚类算法是一种基于最小二乘法原理的迭代优化算法,现如今已经成为被广泛应用的模糊聚类算法。
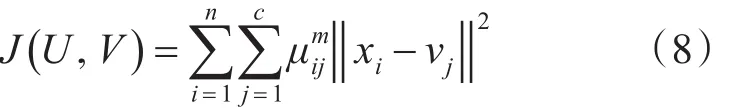
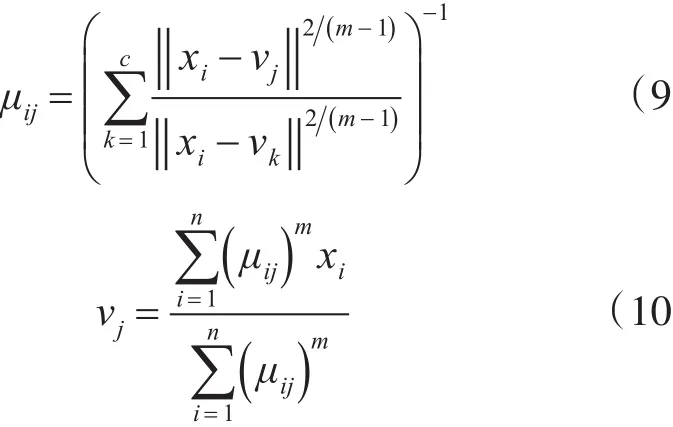
FCM聚类算法的基本步骤如下:
输入:聚类数目c和数据集。
2)根据式(9)计算隶属度Uk;
3)根据式(10)计算下一迭代的聚类中心Vk+1;
模糊C-均值聚类算法具有简单易实现、收敛速度快、局部搜索能力较强的优点。但是该算法对初始聚类中心的选择具有很大的依赖性,同时噪声数据也会对聚类结果的准确性造成很大的影响,这些也是其不可被忽略的缺点。下面将针对其缺点对其进行改进。
3.2 基于混合人工蜂群的模糊C-均值聚类算法
如上面的研究,我们可以知道模糊C-均值聚类算法具有对初始聚类中心的选择依赖的缺点。为了克服这一缺点,提出了基于混合人工蜂群的模糊C-均值聚类算法,其主要是通过混合人工蜂群算法来确定初始聚类中心,再利用FCM聚类算法对初始聚类中心进行优化,最后获得较为理想的最优解。
在基于连续分布估计的人工蜂群算法中,一个蜜蜂的位置向量代表一个聚类中心集合。此时可以定义蜜蜂的适应度函数如下:
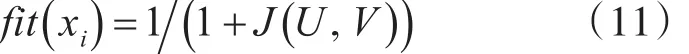
该算法的具体步骤描述如下:
1)设置初始参数:类别数c和模糊指数m,对终止误差ε、跟随蜂的个数(SN)、最大循环次数MCN、Limit这几个参数进行初始化,并设置当前的迭 代 次 数 为 cycle=0;利 用 式(1)初 始 蜜 源,其满足在解空间中依据均匀分布随机生成,同时根据式(11)计算每个蜜源对应的适应度值,利用式(9)和式(10)分别计算出隶属度矩阵U0和初始聚类中心;
2)根据UMDAc-ABC算法的实现步骤计算出聚类中心;
3)根据式(9)更新隶属度矩阵U ;
4)利 用 式(10)更 新 聚 类 中 心 ,并 计 算,当E<ε时,则停止算法;否则转到步骤3)。
4 实验仿真
4.1 基于连续分布估计的人工蜂群算法与人工蜂群算法的对比
为了验证算法性能,将人工蜂群(ABC)算法与基于连续分布估计的人工蜂群(UMDAc-ABC)算法分别对测试函数Sphere和Ackley的仿真结果[20]进行比较。设置测试算法的参数分别如下:SN=100,MCN=100,limit=50。在相同的实验环境下,进行独立实验50次,并记录这50次实验的最好值、最差值和平均值,分别用best、worst和mean表示。其中,最好值和最差值反映出解的质量,平均值反映了该算法的收敛速度。两种算法对测试函数Sphere进行仿真的测试结果如表1所示,它们的结果对比图如图1所示;两种算法对测试函数Ackley进行仿真的测试结果如表2所示,它们的结果对比图如图2所示。

表1 两种算法对测试函数Sphere进行仿真的测试结果
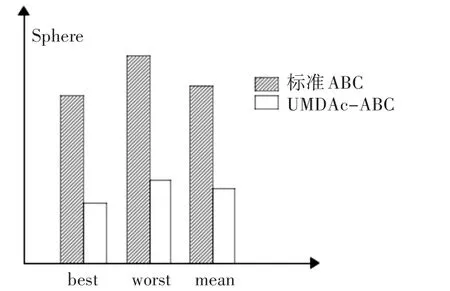
图1 两种算法对测试函数Sphere的结果对比

表2 两种算法对测试函数Ackley进行仿真的测试结果
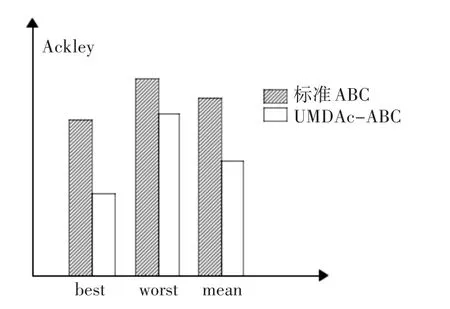
图2 两种算法对测试函数Ackley的结果对比
由以上实验结果可以看出,基于连续分布估计的人工蜂群算法在精度和收敛速度方面都比标准的ABC有着显著的增强。
4.2 基于混合人工蜂群的模糊C-均值聚类算法的仿真与分析
为了验证基于混合人工蜂群的模糊C-均值聚类(UMDAc-ABCFCM)算法的有效性和可行性,这里采用了UCI机器学习数据库中的Wine数据集对该算法进行测试。Wine数据集是产于意大利同一地区不同种植园的3种葡萄酒化学分析结果的样本,它有13个参数作为特征,分为3类,每类分别有60,70,50个,共180个样本,数据为180×13维矩阵。分别用两种算法对Wine数据进行聚类分析,设置算法中允许最小误差ε=10-3,模糊加权指数m=2。蜂群规模SN=100,最大循环次数MCN=100,Limit=50。将两种算法分别运行50次,实验结果如表3所示。
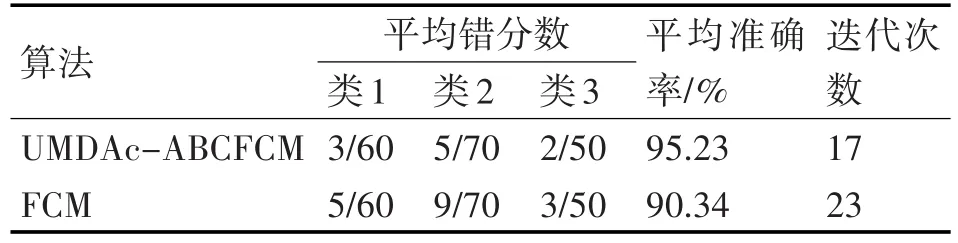
表3 Wine数据的聚类结果
从表3的实验结果可以看出,UMDAc-ABCFCM算法比传统的FCM算法聚类效果更好,不仅准确率得到了提高,而且迭代次数更少,收敛速度也加快了。
5 结语
本文将连续分布估计算法引入人工蜂群算法中,利用分布估计获得的全局信息改进了新的蜜源生成策略,从而提高了算法的全局探索能力,加快了收敛速度。并将此改进的ABC算法应用到FCM聚类算法中,既克服了FCM算法易陷入局部最优解的不足,又弥补了FCM算法对初始值和噪声点比较敏感的缺陷,加快了收敛速度,聚类效果得到了明显的改善。
