一种纹理缺陷特征提取算法∗

吴焕新 岳晓峰 秦伟洋 张鹏飞

（长春工业大学 长春 130012）

1 引言

纹理缺陷特征提取主要分两步进行:首先去除表面纹理，然后提取表面缺陷。

在纹理去除方面，张等设计一种各向异性的背景纹理抑制算子，相同方向的纹理起到最大的互相抑制作用，方向相互正交的纹理不起抑制作用［1～4］；Poesio用局部walsh谱LWS分割纹理和缺陷细节［5～8］；Karthik R用多频带滤波使目标物凸显出来，进而利用阈值分割方法获得图像目标物边界的纹理分割方法［9～11］。这些方法在抑制或去除纹理时难以确定具体的抑制度或阈值，容易造成纹理去除未尽或者缺陷细节损失较多等问题。

在缺陷特征提取方面［12～16］，主要是用缺陷特征参数表示法，经过对图像分割后，通过计算图像的几何或者灰度特征参数来确定缺陷类型，但由于预处理效果的不确定性以及缺陷自身的模糊性，很容易造成误检或漏检。

小波变换具有良好的时域和频域的局域性，能对图像进行多尺度多方向分析。但对于二维图像的边缘如各种曲线等高维奇异性则难以表达。2代Curvelet变换［17］作为在小波变换非线性拓展上的改进，具有更强的稀疏性，能更充分地表达方向细节信息，将其用于纹理缺陷图像的分解，有望得到好的结果。灰度共生矩阵在对角线方向对于反映图像纹理分布特点特别重要，将其与Curvelet变换相结合，能找出纹理特征所对应的高频分量，据此来去除纹理。

核主成分分析［18］作为一种有效的非线性特征提取方法应用很广泛。尤其对于划痕、麻点等细微缺陷，能筛选出实现分类性能最大化的最小特征子集，以降低数据采集的难度和干扰噪声，但在其核参数的选择上大都根据经验来确定，影响了特征提取和降维效果。

基于上述分析，本文提出了一种2代Curvelet变换、灰度共生矩阵和二阶振荡粒子群优化的核主成分分析的纹理缺陷特征提取算法。首先，对纹理缺陷图像进行2代Curvelet分解，分解为低频分量和不同尺度和方向上的高频分量，既降低了训练样本数据的大小，减小了运算量，又使缺陷信息表达更加明显，便于识别。纹理图像的灰度共生矩阵在对角线方向更加敏感。根据特征值大小确定纹理特征所对应的高频分量部分，并予以舍弃。再通过二阶振荡粒子群优化核主成分分析的核参数，利用优化后的核主成分分析对分解去除纹理高频分量后的缺陷样本特征降维，并提取特征信息。在识别缺陷时，通过相似度函数计算每个训练样本特征向量与测试样本特征向量之间的相似度，根据相似度值大小确定测试样本缺陷类型。

2 缺陷训练样本纹理去除

2.1 2代Curvelet变换

定义在二维空间中，x为空间位置参量，ω为频域参量，r和θ为频域下的极坐标。1代Curvelet变换定义为

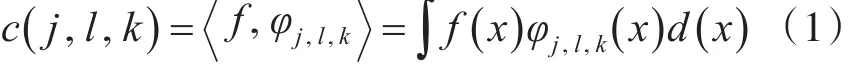
2代Curvelet变换与1代Curvelet变换具有完全不同的构造。在笛卡尔坐标系下，对函数进行FFT变换得到

在每一个尺度j和每一个方向l上得到乘积

围绕原点局部化 f得到

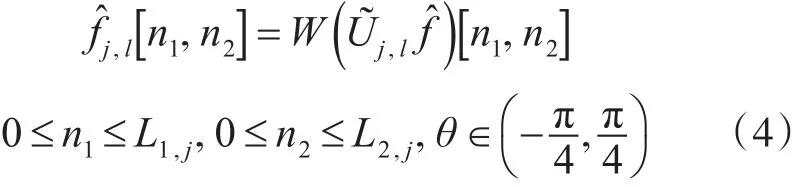
2.2 灰度共生矩阵及纹理去除

灰度共生矩阵用于统计处于同样位置关系的一对像素灰度的相关性，能够有效反映图像关于方向、相邻间隔、变化幅度的综合信息。灰度共生矩阵在对角线方向对于反映图像纹理分布特点特别重要，故本文采用对角线方向的位置算子来计算共生矩阵。共生矩阵的描绘子如下:

元素差异的k阶矩:

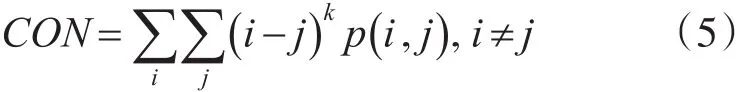
逆元素差异的k阶矩:

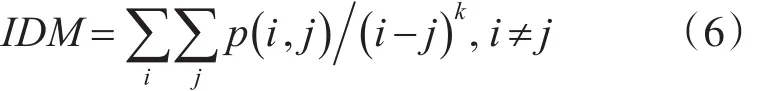
角二阶矩:

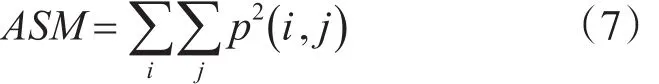
熵:

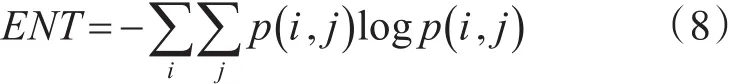
本文对上述四个特征进行加权线性求和，以此作为灰度共生矩阵的特征值。

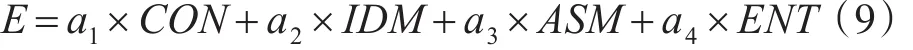
从表1结果可以看出，纹理特征所对应的高频分量的特征值明显高于其它分量，易于从其它高频分量中分离出来，以达到去除纹理的目的。

3 二阶振荡粒子群优化的核主成分分析

3.1 二阶振荡粒子群优化算法

由于原始粒子群算法主要依靠粒子间的协作，粒子本身并没有像遗传算法那样的变异机制，容易受局部极值约束从而陷入局部最优解，无法寻找到全局最优解。为了克服上述缺陷，本文采用了二阶振荡粒子群优化算法，其主要思想是将粒子速度的更新用位置的改变来描述，并且引入了振荡环节，这样可以提高粒子群的多样性，改善全局的收敛性。

假设在N维空间中，粒子在空间中的位置和速度 矢 量 分 别 为 Xi=(x1，x2，…，xn) ，Vi=(v1，v2，…，vn)，粒子i的位置和速度可以分别表示为xi、vi，粒子i当前的最优位置和全局最优位置分别为Mbesti、Nbesti。

将粒子速度的更新引入二阶振荡环节后，其速度的更新公式为

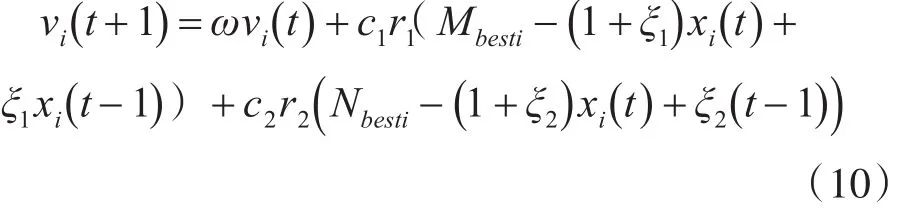
ξ1、ξ2为随机数，在算法前期为了提高粒子群的搜索能力，取阶振荡使粒子下一部运动矢量指向较优的位置，在算法后期，取，通过增强局部搜索能力，使算法逐渐趋于收敛。

3.2 核主成分分析

核主成分分析是对主成分分析的非线性扩展。假设yj( )

j=1，2，…，l 是L个纹理缺陷的训练样本。

设非线性映射为Φ:x→f，则ϕ()yj是由 yj通过非线性映射函数Φ映射到特征空间而得到。假设映射已经满足中心化条件，则特征空间中的协方差矩阵为

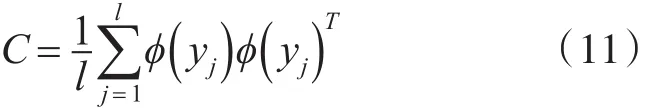
因此，特征空间中的特征方程为

λk(k =1，2，…，l) 和 vk(k =1，2，…，l) 分别为矩阵C的特征值和特征向量，存在参数向量∂k(k =1，2，…，l) 满足:

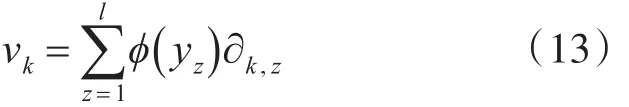
定义一个l×l的核矩阵K，

其中K( )ym，yn为核函数，由式（11）、（12）、（13）、（14）得:

经过变换，核矩阵

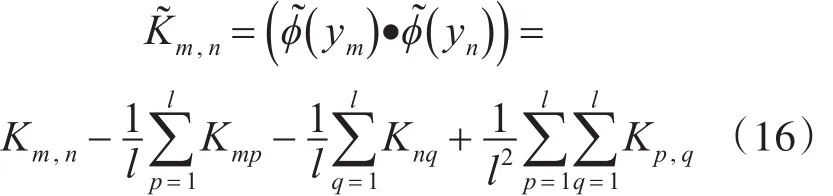
此时，

故测试样本y在特征空间上的投影为

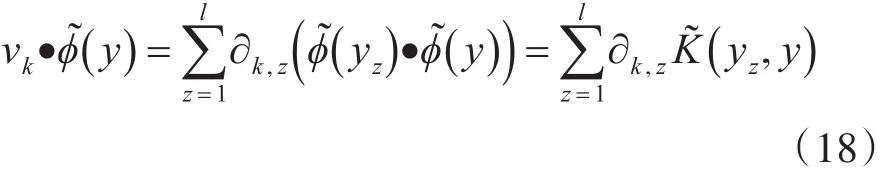
若考虑前n个贡献率达到90%以上的主成分以及对应的权重因子，则综合评价函数为

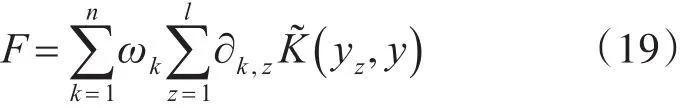
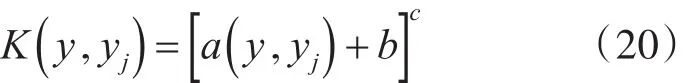
由于对纹理缺陷特征的提取和降维效果受核参数的影响较大，故用二阶振荡粒子群算法选取上述的核参数a、b、c，具体步骤如下:

第一步:设定粒子数为20，自身的学习因子和全局的学习因子均为2，权重因子为0.5，迭代次数为500，问题维数为2。经过大量试验发现，初始化中代表a，b，c的粒子的速度在［-0.15，0.15］之间，搜索位置分别为（0，1.5），（2，3），（1，2）。

第二步:用综合评价函数F的式（19）计算每个粒子的适应值，将第i个粒子的Mbesti设置为其当前最优位置，将Nbest设置为种群最优粒子位置。

第三步:根据式（10）更新粒子位置和速度。

第四步:若达到了局部收敛，计算二阶振荡优化后的粒子的适应值，并与粒子的个体极值和全局极值作比较，保留最优解。

第五步:若达到预设的最大迭代次数，输出全局的最优解。得到a、b、c的最优解后，将其带入式（20）核参数多项式，完成核主成分分析。否则，跳转至第三步。

3.3 用二阶振荡粒子群优化选取核参数

设定纹理缺陷样本核函数多项式:

4 缺陷特征的提取算法

基于2代Curvelet变换、灰度共生矩阵和二阶振荡粒子群优化的核主成分分析提取缺陷特征的算法如下:

1）训练纹理缺陷样本。利用2代Curvelet变换对纹理缺陷图像进行多尺度分解，分解层数为3。对于每一幅纹理缺陷图像y，第一层为低频分量y（1，1），代表的是纹理缺陷图像的背景；第二层为两个高频分量y（1，2，1）、y（1，2，2）；第三层为四个高频分量y（1，3，1）、y（1，3，2）、y（1，3，3）、y（1，3，4）。高频分量主要是反映了缺陷的细节、纹理特征以及部分噪声等信息。

2）纹理缺陷样本去纹理化。对每个高频分量用对角线方向的位置算子计算灰度共生矩阵，并求出其特征值。纹理图像在对角线方向对应的共生矩阵特征值较高，以划痕和凹坑缺陷为例，从表1可以看出，对于具有划痕缺陷的纹理图像，纹理特征主要集中在高频分量y（1，3，3）、y（1，3，4）；而对于凹坑缺陷纹理图像，纹理特征包含于高频分量y（1，3，2）、y（1，3，4）。故在提取缺陷特征时把反映纹理特征的高频分量予以舍弃。

表1 不同尺度高频分量在对角线方向的灰度共生矩阵特征值

对于不同的缺陷，不同尺度和方向下包含的信息对于缺陷识别的贡献不同。例如对于划痕和凹坑这两种缺陷，在舍弃掉纹理特征高频分量后，不同尺度方向上的特征对于缺陷的识别有不同的影响，如表2所示。

表2 不同尺度方向的高频分量对于缺陷样本识别的影响

3）二阶振荡粒子群优化的核主成分分析特征提取。首先，利用二阶振荡粒子群算法优化核参数a、b、c，再利用优化后的核主成分分析提取缺陷特征，参数c为主成分贡献率大于90%的值。例如，选取划痕缺陷样本3个作为输入训练样本，每个样本的像素大小为160×320，提取出来的特征大小为6×3，每个样本用三个主成分表示。划痕训练样本如图1所示，经过特征提取后，图1（a）特征可以用一个向量表示M=[11.4，-25.12，43.17]。

图1 划痕训练样本

4）对纹理缺陷样本测试图像进行2代Curvelet变换，去除包含纹理特征高频分量之后，将剩余高频分量映射到特征空间，得到1×3的特征向量。通过相似性函数计算测试样本特征和每个训练样本特征之间的相似度，相似度最大的训练样本缺陷类型即为测试样本类型，如表3所示。

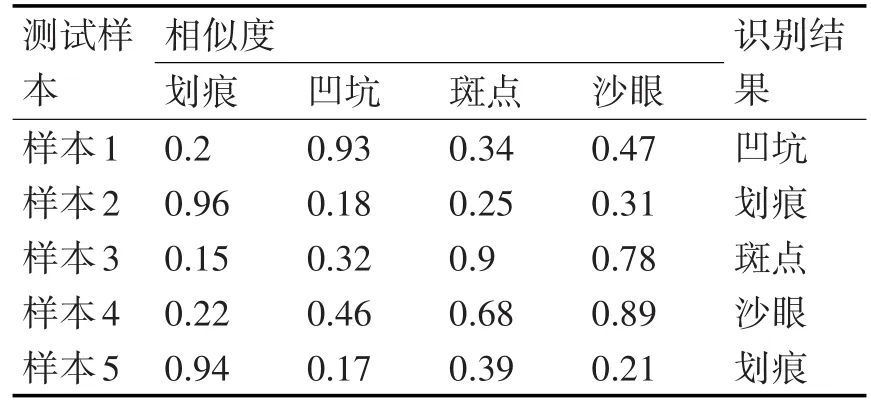
表3 测试样本的识别

5 实验结果及分析

为验证本文算法的适用性，本文采用配置为Intel（R）Core i7，4G内存计算机，分辨率为744×480的IMAGINGSOURCE相机，镜头为50mm长焦镜头，对一块具有纹理的铝合金板进行处理。并与无纹理去除的核主成分分析特征提取法、经本文纹理去除算法后的基于小波变换的核主成分分析法进行对比实验。文中一共选取了划痕、凹坑、斑点和沙眼这四类细微缺陷进行实验，采集了共计360幅缺陷图像，其中训练样本200幅，划痕、凹坑、斑点、沙眼分别为60、50、50、40幅，另160幅图像作为测试样本验证算法的适用性。

经过大量试验，对于划痕、凹坑、斑点和沙眼这四类缺陷特征中，贡献率最大的高频分量依次为y（1，2，2）、y（1，3，1）、y（1，2，1）、y（1，3，2）。利用本文提出的方法对缺陷图像的特征进行识别并与无纹理去除的核主成分分析特征提取法（KPCA）和经本文纹理去除算法后的基于小波变换的核主成分分析法（WKPCA）进行比较。这三种方法的第1主成分贡献率和缺陷识别情况分别如表4所示。

从表4中可以看出，核函数的参数经过二阶振荡粒子群优化后，样本缺陷特征的第一主成分贡献率比不优化直接用核函数分析提取特征（KPCA）时提高了4%左右，改善了特征提取效果。在缺陷特征正确率方面，本文算法明显高于前面两者，因为一方面经过2代Curvelet变换后，舍弃了包含纹理特征的高频分量，避免了纹理对缺陷识别的干扰，而且保留了反映缺陷主要细节的高频分量，而小波变换虽然也可以进行分解，但无法充分表达方向细节信息制约了特征提取完整性。另一方面核参数经过二阶振荡粒子群优化后，识别率明显提高。

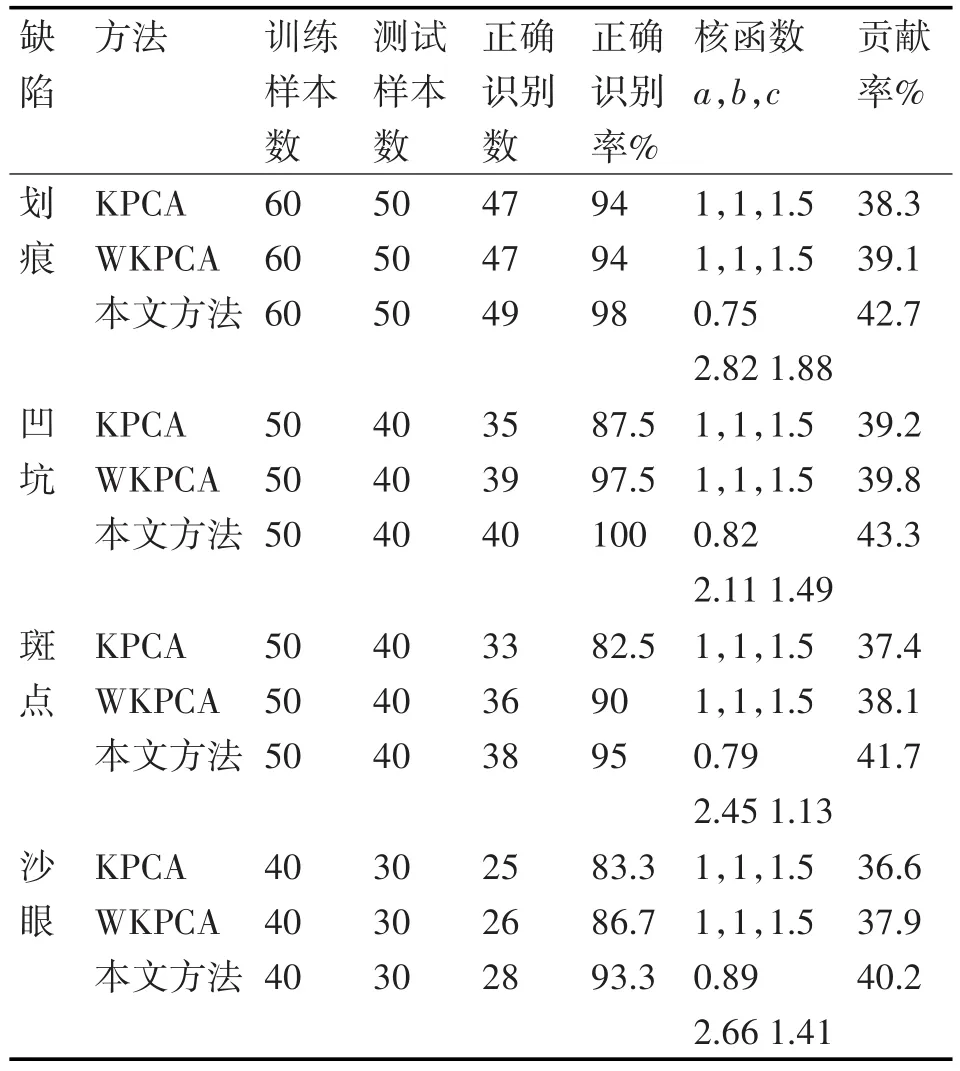
表4 四种缺陷识别情况及第1主成分贡献率

6 结语

1）本文给出了用二阶振荡粒子群优化核主成分分析的算法。该算法可以明显提高样本缺陷第1主成分的贡献率，有效改善了缺陷特征提取效果。

2）提出了一种基于2代Curvelet变换和二阶振荡粒子群优化核主成分分析的提取缺陷特征的算法，利用2代Curvelet变换把样本特征分解为不同尺度和方向的高频分量，利用对角线方向的位置算子求解灰度共生矩阵的特征值，确定了纹理特征所对应的高频分量，并予以舍弃。利用二阶振荡粒子群优化的核主成分分析提取的缺陷训练样本和测试样本的特征可靠。

3）与无纹理去除的核主成分分析方法和经本文纹理去除算法后的基于小波变换的核主成分分析方法相比，本文所提出的算法核参数选择更精确，样本缺陷特征识别率更高。