kd-tree建树算法改进

2019-06-01廖勇毅丁怡心

现代计算机 2019年12期

关键词：建树子树方差

廖勇毅，丁怡心

（广州民航职业技术学院计算机系，广州 510403）

kd-tree（k-dimensional tree 的简称）是一种分割k 维数据空间的数据结构，主要应用于多维空间特征向量的快速搜索。但是kd-tree 的重要缺点是建树速度非常慢，提出一种改进的建树算法，可显著提高建树速度。

kd-tree；建树优化

0 引言

kd-tree（k-dimensional 树的简称），是一种分割k维数据空间的数据结构。主要应用于多维空间特征向量的搜索。kd-tree 是一种轴对齐的BSP 树，其具有场景自适应划分、低存储消耗和快速遍历等优势，特别是对高维数据具有很好的自适应划分效果，常用于在大规模的高维数据空间进行最近邻查找（Nearest Neighbor）和近似最近邻查找（Approximate Nearest Neighbor），例如图像检索和识别中的高维图像特征向量的K近邻查找与匹配。

1 kd-tree的数据结构

kd-tree 从空间角度看待存储的数据，并采用树形结构划分和组织场景空间。当存储二维数据时，存储空间就是一个二维平面。根节点按照某一维索引中的某个值M1 把数据划分成左右两部分，所有在该维小于等于M1 的数据都放在L1 的左子树，所有大于M1 的数据都放在的右子树R1。接下来如果左子树L1 或右子树R1 拥有大于1 个节点，则用同样的方法对它们进行划分。

2 kd-tree建树算法分析

kd-tree 建树的基本思想是一直二分下去，直到所有子树都只有一个节点为止。对于多维数据，首先需要选则一个维度来进行二分，然后需要在该维度上选择一个分割点，再把在该维度上小于等于分割点的节点都放在左子树，把在该维度上大于分割点的节点都放在右子树，最后如果子树拥有大于1 个节点，则用同样的方法递归分割子树。

举一示例：假设有7 个二维数据点={（0，3），（2，2），（3，3），（4，2），（6，1），（7，2），（7，4）}，数据点位于二维空间中。为了能有效的找到最近邻，kd-tree 采用分而治之的思想，即将整个空间划分为几个小部分。7 个二维数据点生成的kd-tree 如图1 所示。

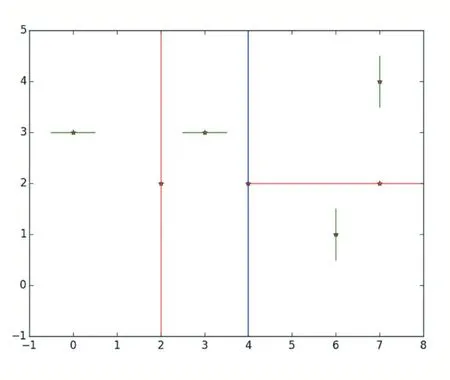
图1 kd-tree建树演示

3 建树算法描述

（1）确定候选分割维度：对于所有描述子数据（特征矢量），统计它们在每个维上的数据方差。以SIFT特征点为例，描述子为128 维，可计算128 个方差。挑选出最大值，对应的维就是分割平面（对于多维数据就是超平面）。数据方差大表明沿该坐标轴方向上的数据分散得比较开，在这个方向上进行数据分割有较好的分辨率；

（2）从候选分割平面中选择最优的分割位置，通常是取该维度上的中间点作为分割点；

（3）以分割点为中心把数据分成左子树和右子树；

（4）对于左、右子树的数据集，按（1）、（2）、（3）步递归处理直到每个子树只有一个节点。

4 选择分割维度

研究kd-tree 是为了优化在一堆数据中高频查找的速度，用树的形式，也是为了尽快地缩小检索范围，所以这个“比对维”就很关键，通常来说，更为分散的维度，就更容易的将数据分开，是以通过求方差，用方差最大的维度来进行划分，即最大方差法。用下面公式计数据在某一维度上的方差。

5 选择分割点

确定了分割维度后，需要在该维度上选择一个分割点，以此作为kd-tree 的根（root）。选择分割点的原则有两点：①保证树的平衡；②保证叶子节点所占的空间大致相等。第一点是为了降低搜索树的平均效率，一个极端不平衡的树会让搜索的时间复杂度变成O（N），而不是O（logN）。第二点则最大限度地提高了搜索的精度。

1987年，Omohundro 提出选择分割维度中心点做为分割点的思想，这种思想能最大限度实现树的平衡，但是分割的叶子节点空间不均匀，很多叶子节点在非常细小的空间，导致搜索精度受到影响。当需要进行精准搜索是，要经过多次搜索，使得搜索性能大大下降。

选择最靠近分割维度空间中间位置的点作为分割点，是一种较好地折中平衡性和分割空间的思想，虽然树的分布出现部分不平衡，但是分割的叶子空间基本相等，大大提高了搜索精度，通常一次搜索就可以精确匹配，提高搜索性能。

6 改进建树算法

kd-tree 建树的时间复杂度为O（N*N*M），其中N为特征点数量，M 为特征点维数。当候选特征点数量很大时建树速度很慢，算法最耗费时间的部分是每次确定候选分割平面前统计每维上的数据方差。针对建树速度慢的问题，提出对于所有描述子数据（特征矢量），取一定数量t 作为样本，统计它们在每个维上的数据方差。于是，kd-tree 建树的时间复杂度变为O（t*t*m），当t 的值选择得当时，可大大提高建树的效率，并且对kd-tree 搜索的准确性影响非常小。

在实际工程中可以选取间隔相等的t 个特征点做为样本，例如：特征点数N=100000，确定统计样本树t=1000，则每隔100000/1000=100 个特征点选1 个作为样本。

改进算法代码实现：

输入：①特征点数组；②特征点个数

输出：选取维度