基于改进层次分析法的特殊体型样板识别

2019-05-30马秋瑞黄晓杰

纺织学报 2019年5期

周捷，李健，马秋瑞，黄晓杰

(1. 西安工程大学服装与艺术设计学院，陕西西安 710048； 2. 中原工学院信息商务学院，河南郑州 450007)

样板识别是服装纸样制作、服装合体性评价及开发智能打版系统的重要步骤[1-2]。在识别过程中，由于人体体型、结构修正规则和专家意见存在极大的模糊性，以致特体样板处理技术的薄弱成为了服装企业面临的严峻问题。目前学者通常采用单一的定性分析或定量计算法，如局部样板修正[3-4]、智能纸样生成[5-7]、纸样尺寸预测[8-9]等。然而，特体样板识别是多目标、多层次的综合评价问题，且存在诸如腹凸溜肩样板、挺胸平肩样板等大量复合特体样板，传统定性或定量方法难以进行数学表达，因此必须用一套科学的方法对特体样板评价指标体系进一步完善和研究。

指标权重的确定是特体样板识别的关键因素。目前，国内外关于特体样板识别还没有合理的识别模型和评价标准，缺乏运用数学分析方法建立的特体样板评价体系。近年来，层次分析法(Analytic Hierarchy Process，AHP)因可将定性问题定量化，在多层次复杂系统的识别中得到广泛应用[10-11]，但是，传统层次分析法在确定权重系数时依赖于专家意见的主观判断，其结果缺乏客观性[12]。基于此，本文提出一种结合因子分析、聚类分析的改进层次分析方法，构造特体样板特征指标体系并进行量化，最后进行实证分析。实例分析验证该方法的有效性，克服层次分析法量化标度时产生的主观性影响，保证识别结果的客观准确。

1 实验部分

1.1 数据来源

本文以国内某公司近两年处理的特体男西服修正样板为研究对象。该公司专为德国特殊体型客户提供西服定制服务，本文研究共收集到478个特体样板。

1.2 数据预处理

人体体型是服装结构设计的基础，由于特殊体型与正常体型存在一定的差异，样板师需要依据客户各部位实际尺寸对基础样板进行修正,最终得到适合该客户的修正样板。修正样板与基础样板各部位尺寸的差值本文称之为修正量。本文通过对样本数据进行正态分布检验、奇异值检查、缺失值处理和相关性分析，并剔除修正频率较低等指标，最终保留367个有效样本。在分析样板过程中，发现95%以上的样板都是左右对称的，故在本文研究中统一选取右侧数据作为研究对象，共获得13项分析指标，如图1所示。

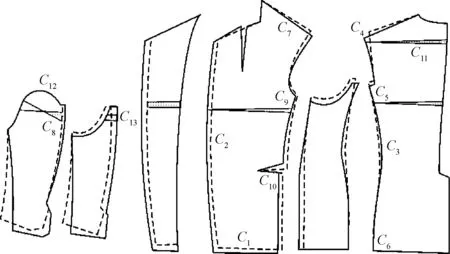
图1 特体修正样板的典型指标Fig.1 Typical index of special body correction model

4项长度指标：前衣长修正量(C1)、前中长修正量(C2)、后片侧缝腰长修正量(C3)和肩斜修正量(C4)。

4项围度指标：胸围修正量(C5)、臀围修正量(C6)、肩宽修正量(C7)和侧片后袖窿点左右修正量(C8)。

5项部位指标：前胸宽修正量(C9)、腹省大小修正量(C10)、肩胛省修正量(C11)、小袖山弧线上下修正量(C12)和后袖缝修正量(C13)。

1.3 研究方法

层次分析法的基本原理是将评价指标两两比较判断，确定每个层次中各因素相对于上一层或最高层总目标的相对重要性，并加以排序[13-14]。在实际应用中，通常包括以下4个步骤[15]:1)建立层次结构模型；2)构建判断矩阵；3)层次单排序及一致性检验；4)层次总排序及一致性检验。

层次分析法虽具有简化复杂问题的优点，但其在量化标度时存在主观性较强的局限性。为较全面地考虑特体样板的影响因素，本文应用改进层次分析法建立了特体样板识别的层次结构模型，即采用因子分析和聚类分析对各影响因素进行权重量化，使得权重大小更符合工程应用实际。指标体系构建流程如图2所示。

图2 改进层次分析法流程图Fig.2 Flow chart of improved analytic hierarchy process

2 结果与分析

2.1 因子分析

经KMO(Kaiser-Meyer-Olkin)样本测度和巴特利特球形检验(Bartlett′s test)，得到KMO值为0.622，大于0.5，Bartlett检验的Sig.值小于0.05，说明样本数据适合作因子分析。

在SPSS 22.0软件中利用主成分法提取因子，得到各因子的特征值与方差贡献率如表1所示。按特征值大于1和累计贡献率大于70%的原则[16-17]，提取5个主成分，其累计方差贡献率达到73.55%。

表1 主成分因子分析Tab.1 Principal component factor analysis

表4 3类特体样板主要部位平均修正量统计表Tab.4 Statistical table of average corrections for main parts of three specialty samples mm

采用方差最大化正交旋转得到因子载荷矩阵，如表2所示。可以看出，主成分因子F1在C2、C3、C5、C6和C9上有较大载荷系数，将其称为廓形因子B1；主成分因子F2在C8和C13上有较大载荷系数，将其称为袖窿因子B2；主成分因子F3在C1、C7和C10上有较大载荷系数，将其称为躯干因子B3；主成分因子F4在C12上有较大载荷系数，将其称为袖山因子B4；主成分因子F5在C4和C11上有较大载荷系数，将其称为肩部因子B5。

表2 旋转载荷矩阵Tab.2 Rotational load matrix

2.2 聚类分析

以因子分析提取的5个主成分为聚类指标，聚类数依次定为3～5进行K-means聚类，方差分析表见表3。聚类结果显示，显著性水平Sig.值均小于0.005，表明3种聚类结果均可接受。同时，当聚类数为3时，类间均方最大，误差均方最小，F值最大，即此时因子间的差异最大，聚类结果最清晰。因此，特体样板聚成3类是比较合理的。

表3 方差分析表Tab.3 Variance analysis table

当聚类数为3时，所包含的特体样板统计信息见表4。依据样板统计特征分别命名为：臀部特体样板(D1)、胸部特体样板(D2)和腹部特体样板(D3)，对应样本数为214、93和60。

2.3 样板识别

2.3.1 建立层次结构模型

建立科学可行的层次结构模型是确定指标权重的首要问题。综合因子分析和聚类分析结果，建立特体样板识别模型的递阶层次结构见图3所示。层次结构模型说明如下：1)目标层A：对特体样板进行识别。2)准则层B：将特体样板用因子分析提取的五个主成分进行描述，分别是：B1、B2、B3、B4和B5。3)子准则层C：将5个主成分指标具体描述为13项特体样板主要控制部位。B1以C2、C3、C5、C6、C9来表示；B2以C8、C13来表示；B3以C1、C7、C10来表示；B4以C12来表示；B5以C4、C11来表示。4)方案层D：以聚类分析所得的3类特体样板为备选方案，依据表4中部位平均修正量将待识别特体样板进行判别归类。分别记为D1、D2和D3。

图3 特体样板识别模型的递阶层次结构Fig.3 Hierarchical structure of special template recognition model

2.3.2 构建判断矩阵

在建立递阶层次结构后，采用九标度法[18]构造B→A，C→B和D→C的各层次判断矩阵。标度aij表示同一层各元素相对相邻上一层元素的两两重要性比较，如表5所示。

表5 判断矩阵标度aij含义Tab.5 Judgment matrix scale and its meaning of aij

1)B→A层：由表1中5个主成分因子的方差贡献率(B1：21.076%、B2：17.777%、B3：16.840%、B4:9.800%及B5：8.057%)，依据B层元素相对于目标层A的相对重要程度，构造权重判断矩阵B-A及相关数据见表6。

表6 特体样板识别判断矩阵B-ATab.6 Special sample recognition judgment matrix B-A

一致性检验[18]：一致性指标CI为5.9848e-4，一致性比率CR为5.3435e-4，小于0.1，检验通过。

2)C→B层：由因子载荷矩阵中5个公因子的系数，依据C层元素相对于指标层B的相对重要程度，构造5个判断矩阵。权重判断矩阵C-B1表示C层元素相对于准则层B1元素的相对重要程度，其相关数据见表7。

表7 廓形因子判断矩阵C-B1Tab.7 Profile factor judgment matrix C-B1

一致性检验：一致性指标CI为0.049 0，一致性比率CR为0.043 8，小于0.1，检验通过。

同理，可分别构造三级指标的其他4个判断矩阵。经计算，所有判断矩阵的一致性比率CR值均小于0.1，符合完全一致性。限于篇幅，各个指标的计算过程不详细列出。最终，权重判断矩阵C-B2、C-B3、C-B4和C-B5的综合权重分别为(0.750 0,0.250 0)、(0.637 0,0.104 7,0.258 3)、1和(0.166 7,0.833 3)。

3)D→C层：计算待识别样板与三类特体样板对应部位平均修正量的差值大小，如表8所示，构建D→C层的判断矩阵。

随机选取3个待识别样本进行实证研究，样本分别编号为a、b、c。依据13项主要分析指标的相对重要性进行两两比较，构造四级指标的判断矩阵。以样本a为例，权重判断矩阵D-C1的综合权重为(0.081 0,0.188 4,0.730 6)，其一致性检验CI为0.032 4，一致性比率CR为0.062 4，小于0.1，检验通过。

同理，可构造D→C层其他12个判断矩阵。鉴于被测样本b、c步骤与样本a完全相同，故在此不再赘述。

2.3.3 层次单排序及一致性检验

确定判断矩阵后，采用方根法计算特征值与特征向量，得到的特征向量即权重分布。由下式确定相对于上一级指标的相对重要性，即单层权重值wi。而后，计算4级指标相对于一级指标的相对重要性，即总权重。

式中：aij为判断矩阵中第i行第j列的元素。

2.3.4 层次总排序及一致性检验

通过以上各元素判断矩阵，计算A层到D层中各级指标的权重乘积计算，得到总排序权重。通过权重的排序得出特体样板识别模型的隶属度，依据最大隶属度输出综合识别结果，被测样本a层次总排序，如表9所示。

表8 待测样本与特体样板主要部位尺寸差值大小Tab.8 Difference between the size of the main part of the sample to be tested and the special sample mm

注：Δa1为样本a与特体样板1的差值；Δa2为样本a与特体样板2的差值；Δa3为样本a与特体样板3的差值,以此类推。

表9 指标层总权重计算和排序Tab.9 Index layer total weight calculation and sorting

注：表中W1表示样本a对样板D1的总排序权重；W2表示样本b为样本D2的总排序权重；W3表示样本c对样板D3的总排序权重。

同理，被测样本b的总排序综合权重为(0.110 8,0.524 2,0.357 6)，被测样本c的总排序综合权重为(0.422 6,0.243 3,0.334 1)。

经计算，所有判断矩阵的CR值均小于0.1，各判断矩阵均满足一致性检验的要求。

3 讨论

特体样板是由体型的多样性、复杂性以及结构的不确定性因素组成的复杂系统，如何量化特体样板的定性特征指标是一项挑战。针对传统AHP法的不足，本文应用改进AHP法建立了特体样板的层次结构模型，并探讨了该模型在特体样板识别中的具体途径。结果显示，层次分析法结合因子分析、聚类分析可用于特体样板识别。

在本文的因子分析中，将原有13项分析指标精简为5个主成分，分别记作F1-F5，保留了超过70%的原始数据信息，这大大降低了指标的复杂性[19]。根据旋转载荷矩阵的结果，将特体修正样板的13个分析指标值进行标准化之后与其指标权重相乘，得到特体样板5个主成分的因子得分函数：

根据各因子的方差贡献率进行加权平均，得特体样板综合得分F，即:

在本文的聚类分析中，聚类分析作为一种无管理模式的识别方法，聚类结果在很大程度上取决于方法所采用的距离、类间距等参数[20]。根据表4绘制雷达图，如图4所示，以更直观地比较3种特体样板聚类类别的差异。由图可知，第1类样板D1中，指标C6、C9在所有类别中最大，且C6差异显著。指标C3和C10显著低于另外两类，在指标C1和C4上居中。该样板特征为偏胖型，臀部丰满浑圆，长度中等；第2类样板D2中，指标C8、C11和C13在所有类别中最大，且差异十分显著。指标C1显著低于另外两类，指标C3和C10居中。该样板特征为矮胖型，腰围线附近肥胖宽大，腰部适中，衣长短小；第3类样板D3中，指标C1、C10在所有类别中最大，且差异十分显著。指标C4、C8和C13显著低于另外两类，指标C9居中。该样板特征为高瘦型，腹部长而扁平，围度较瘦，胸宽适中。