开裂钢筋混凝土梁的车致振动研究
2019-05-30陈兴达朱劲松
陈兴达,朱劲松,b
(天津大学 a.建筑工程学院,b.滨海土木工程结构与安全教育部重点实验室,天津 300072)
运营中的钢筋混凝土桥梁,会因设计失误、超载以及自然灾害等原因产生裂缝,这些存在于结构当中的裂缝层对桥梁整体的性能产生影响。结构体中能够随着结构运动张开和闭合的裂缝被称为“呼吸裂缝”,桥梁中的大部分裂缝均属此类。在车辆荷载的冲击作用下,呼吸裂缝的开合现象会被放大,甚至对桥梁整体动力性能产生影响。因此研究呼吸裂缝对桥梁整体振动的影响对于桥梁结构的损伤识别及性能评估具有指导意义。
在进行开裂结构的动力分析时,呼吸裂缝的模拟主要有以下两种模型。第一种模型称之为呼吸裂缝的损伤函数模型。LAW et al[1]通过在WAHAB et al[2]提出的静力作用下裂缝的损伤函数模型中加入与车辆荷载运动速度有关的参数来模拟呼吸裂缝的特殊性质,并用T梁模型进行试验验证,研究了受损T梁的动力响应。殷新锋等[3]也用呼吸裂缝损伤函数模型研究了开裂混凝土连续梁桥的动力响应。第二种模型称之为呼吸裂缝的扭簧模型。LEE et al[4]运用欧拉梁理论和假设模态法将梁体以断裂面为界分成两段独立的梁,断裂面的转动不连续则用扭簧进行模拟,研究了移动荷载作用下不同荷载大小和裂缝大小对开裂梁振动特性的影响。CHENG et al[5]假设模型中的扭簧刚度以均值为中心呈频率与一阶振型频率相等的正弦式变化,研究了开裂悬臂梁的振动响应。ARIAEI et al[6]则假设模型中的扭簧刚度与当前曲率和最大曲率有关的函数变化,用离散元法和有限元法对移动荷载作用下开裂简支梁的动力响应进行了参数分析。呼吸裂缝的损伤函数模型虽能体现呼吸裂缝在车辆荷载作用下刚度的改变,但它是在开裂截面一定区域范围内对梁的刚度进行折减,未能体现呼吸裂缝内部作用的本质,应用时比较麻烦。而对于呼吸裂缝的扭簧模型目前提出的扭簧刚度的变化函数均未能考虑到车辆荷载的特殊性,不宜用在桥梁的车致振动研究中。
为了研究呼吸裂缝对车辆荷载作用下开裂钢筋混凝土梁振动性能的影响,本文首先给出了常用的呼吸裂缝的定刚度模型,并以此为基础,通过设定混凝土裂缝的传力宽度阈值,建立了车辆荷载作用下混凝土裂缝的变刚度模型;接着采用分离式分析方法编制了开裂钢筋混凝土梁与车辆荷载的耦合振动分析程序;最后,以开裂的钢筋混凝土简支梁为例,分析了不同裂缝模型的异同,并研究了车辆荷载大小对开裂钢筋混凝土梁振动性质的影响。
1 呼吸裂缝模型
1.1 定刚度模型
为使问题简化,在此仅考虑在弯矩作用下的开裂Euler-Bernoulli梁。梁的参数如图1所示,其中h表示梁高,a表示裂缝的名义深度。θ表示弯矩M作用下裂缝的名义局部转角。若设裂缝所在截面的柔度系数为Cm,则θ和M的关系式可表示为:
θ=CmM.
(1)
柔度系数Cm可通过断裂力学分析得到:
(2)
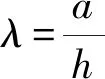
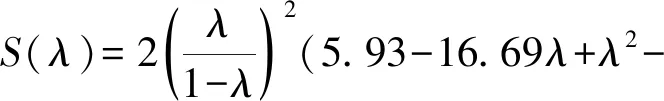
(3)
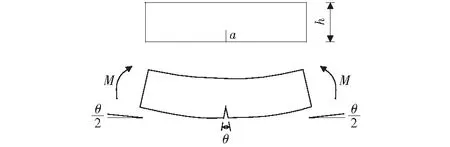
图1 开裂梁示意图 Fig.1 Schematic diagram of cracked beam
建立裂缝的定刚度模型梁时,通常将梁体在裂缝所在截面处分开,并用线性扭簧连结,如图2所示,此时扭簧的刚度为:
(4)

图2 扭簧连接示意图 Fig.2 Schematic diagram of torsion spring connection
1.2 变刚度模型
GUDMUNDSON[8]在研究裂缝位置及深度与结构自振频率关系试验中最早发现了裂缝闭合效应引起的结构非线性振动现象。ALLISON et al[9]通过对开裂的Ti-6242S进行精确的试验,观察到即使是在一定的正向拉力的作用下裂缝也会保持闭合状态。这些研究表明考虑裂缝的闭合效应是有必要的。
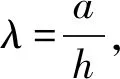
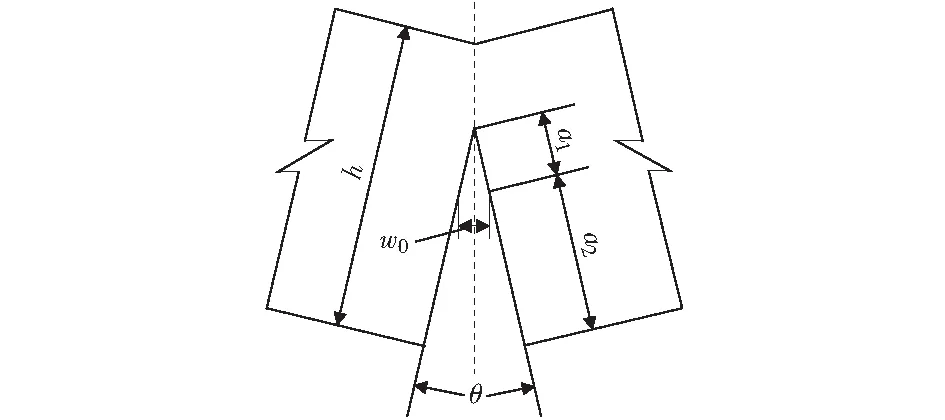
图3 放大的裂缝示意图 Fig.3 Schematic diagram of amplified crack
根据前面的假设,由几何关系可得:
(5)
a2=a-a1.
(6)
(7)
公式(7)中的裂缝截面名义转角θ可用名义损伤比λ由式(1)和(2)计算得到,即:
(8)

呼吸裂缝从完全闭合转变到部分闭合张开状态,存在临界弯矩M0,令公式(8)中的λ′=0,可得:
(9)
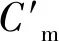
kc=ζk0.
(10)
由以上的分析可得呼吸裂缝的变刚度模型的刚度表达式:
(11)
进一步可绘出考虑裂缝截面的闭合效应后呼吸裂缝所在截面的实际局部转角θ'与截面弯矩的关系图,如图4所示。
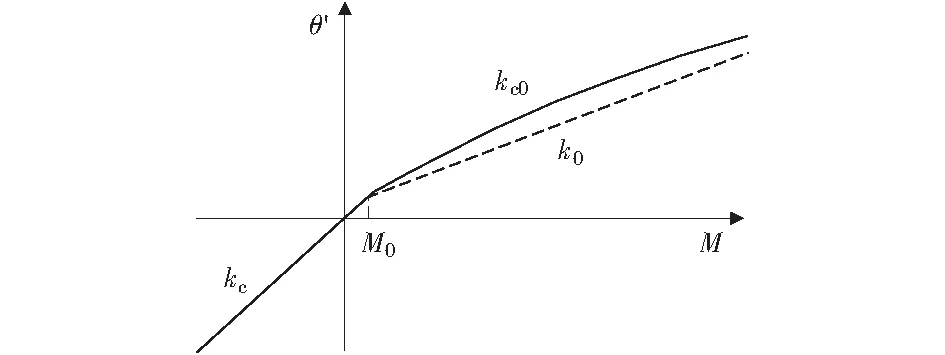
图4 裂缝截面实际转角与所受弯矩关系图 Fig.4 Relationship between true opening angles of cracked section and bending
1.3 裂缝传力宽度阈值的确定
很多试验表明,混凝土裂缝端部存在着微裂缝区,并伴有主裂缝的亚临界扩展,根据这些实验观察结果,徐世烺等[10-11]提出了采用CTOD作控制参数的混凝土窄带断裂区模型。在此则用w0作为裂缝的传力宽度阈值,满足呼吸裂缝变刚度模型的假设。
直接测定CTOD是很困难的,一般利用三点弯曲梁的变形,由简单的几何关系间接地测量CTOD。把CTOD看成主要是由于裂缝的亚临界扩展对缝端开口位移的贡献,得到混凝土三点弯曲试件的CTOD即w0的计算表达式:
(12)
式中:lFC是临界裂缝断裂区长度的实测值,开口位移临界值lC可取与最大值荷载pmax对应的开口位移值。混凝土构件的CTOD值可参考文献[10]获得。本文取混凝土裂缝的传力宽度阈值w0等于CTOD值,即w0=0.022 82 mm.
2 车桥动力系统建模
2.1 开裂梁模型
如图5所示,跨径为L的开裂简支Euler-Bernoulli梁,裂缝与左支点的距离为L1.Ff和Fb分别表示车辆前轴和后轴对梁的作用力,d表示前后轴的距离,v是车辆的行驶速度,则t时刻车辆后轴与左支点距离为vt.
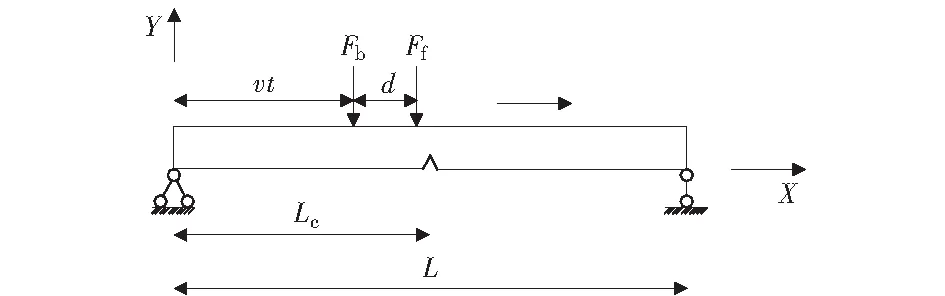
图5 车辆荷载作用下开裂梁示意图 Fig.5 Schematic diagram of cracked beam under vehicle load
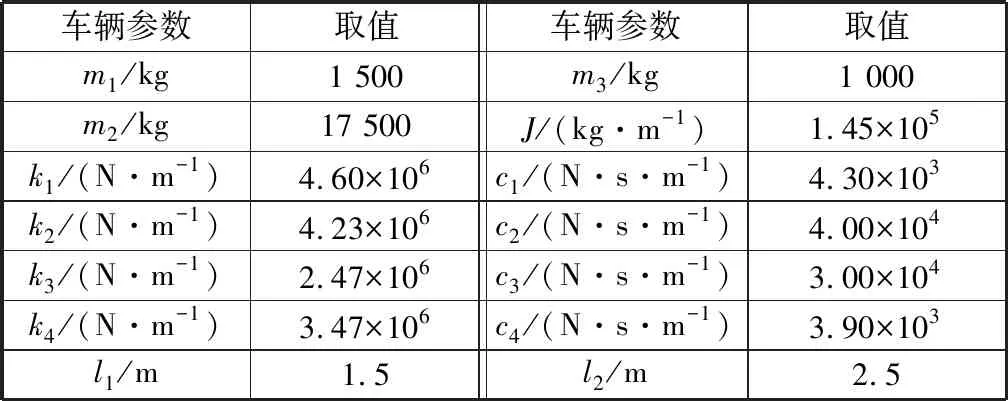
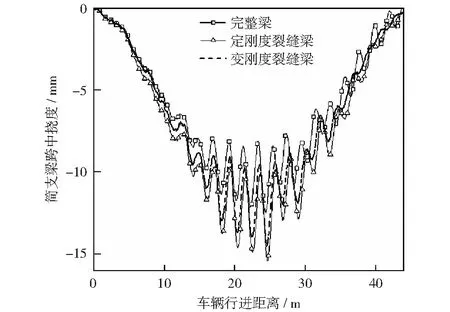
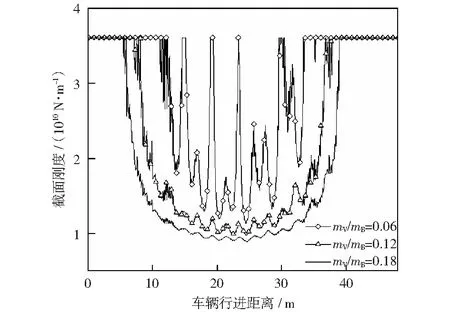
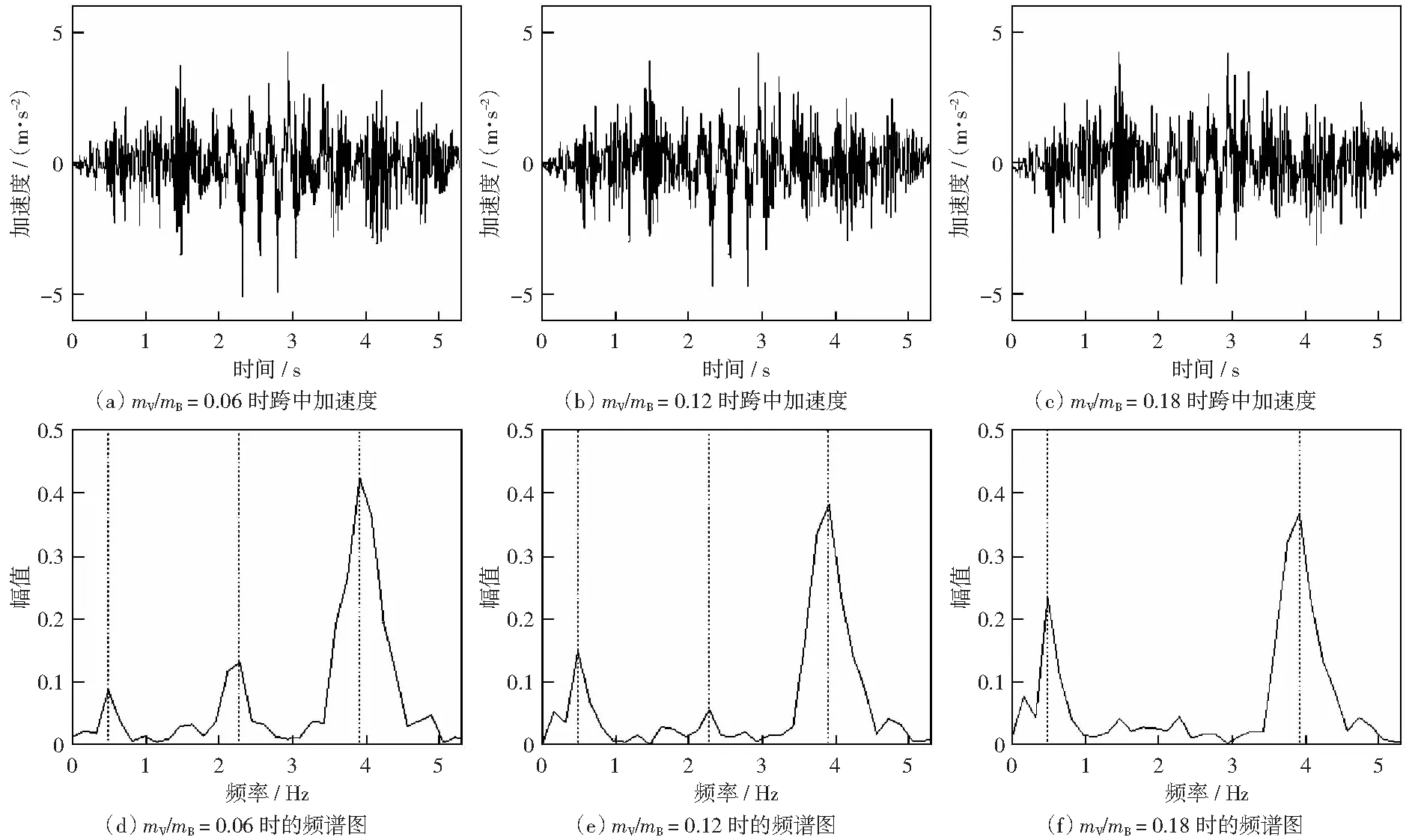
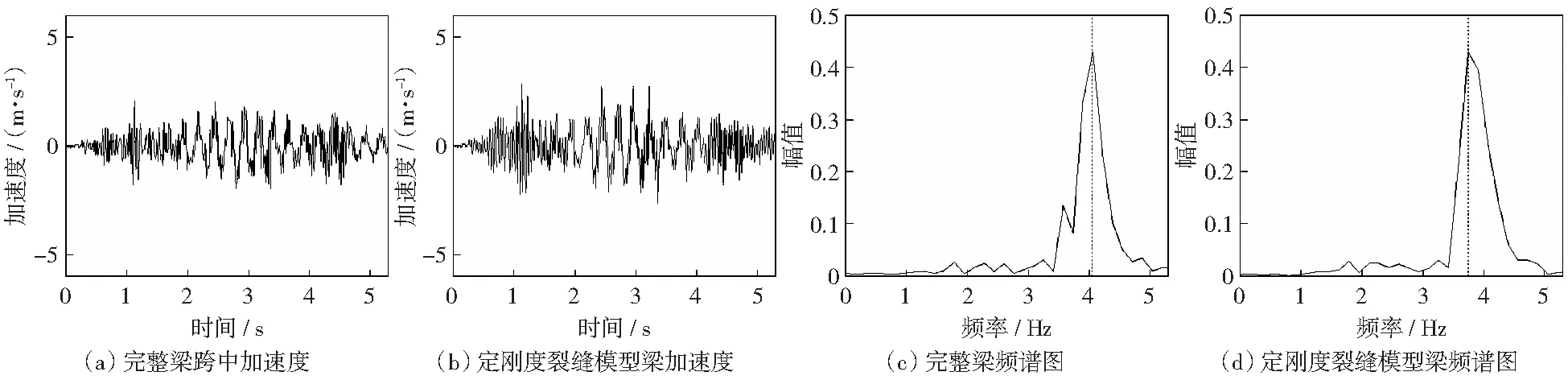
考虑单裂缝的情况,将梁以裂缝为界分成两段,并用扭簧连接。设梁的挠曲线表达式为yi(x,t),i=1,2分别表示0 (13) 式中:E,I,ρ和A分别表示梁的弹性模量、抗弯惯性矩、密度和横截面积。δ是狄拉克δ函数,该函数在除了0以外的点都等于0,而其在整个定义域上的积分等于1。 简支梁的边界条件为: y1(0,t)=0,y"1(0,t)=0, (14) 裂缝截面处的协调方程为: (15) 式中:k为定刚度模型中线性扭簧刚度k0或变刚度模型中非线性扭簧刚度k1. 车辆模型采用简化后的两轴车力学模型[12],车辆模型的布置和参数定义如图6所示。车辆的动力方程可写成: MvY"v+CvY'v+KvYv=Fv. (16) 式(16)中的质量矩阵Mv、刚度矩阵Kv、阻尼矩阵Cv荷载列阵Fv分别可表示成下列形式。 图6 车辆模型 Fig.6 Model of vehicle 当车重为20 t时的车辆参数值见表1。 表1 车辆模型参数Table 1 Parameters of vehicle model 路面不平顺r(x)是车致振动的主要影响因素,它可采用三角级数叠加法来进行模拟: (17) 式中:r(x)为路面不平顺样本函数,αk为余弦函数的幅值;ωk是位于功率谱密度定义区间[ωl,ωu]内的频率;θk为均匀分布在0和2π之间的随机相位角,x为局部坐标,表示桥上某点距桥梁左端的距离,N为模拟随机不平顺的点数。α是不平顺系数,指数β可取1.94[13].桥上路面粗糙度被划分为5个等级,各等级路平顺系数见文献[13]. 在进行车桥耦合振动分析时,通常假设车辆在行驶过程中始终与梁体保持接触状态,车辆的动力方程和梁的动力方程可通过接触点处作用力和位移的相互约束进行耦合。以车辆后轮为例,车轮与梁体的相互作用力可表示成: (18) 式中:δb(t)表示后轮质心在t时刻相对于梁体的垂直位移,其表达式为: δb(t)=yb(t)-zb(t)-rb. (19) 式中:yb(t)为后轮质心在t时刻的竖向位移,zb(t)为接触点处桥面节点在t时刻的竖向位移,rb为后轮与桥面接触点处的桥面不平顺样品值。 车辆与梁的耦合方程是一个时变的二阶微分方程组,一般只能用数值法进行求解。在求解时,采用Newmark-β法,编制了MATLAB与ANSYS联合程序对车桥耦合方程进行迭代求解。 以移动车辆荷载作用下的开裂钢筋混凝土简支梁为例进行分析。钢筋混凝土简支梁跨径L=40 m,截面面积A=0.58 m2,截面惯性矩I=0.69 m4,弹性模量E=53.5 GPa.未开裂时,简支梁的一阶振动频率为4.10 Hz.因为简支梁的跨中部位是最容易发生破坏的,所以在进行车桥耦合振动分析时,假设梁体的初始裂缝位于跨中,且裂缝的名义损伤比λ=0.3.车辆荷载的参数根据表1按比例确定,并取车辆的行进速度为30 km/h,路面不平顺等级则选一般。 为了对比,共建立3种模型:完整梁、定刚度裂缝梁和变刚度裂缝梁。定刚度裂缝梁中裂缝截面处扭簧的刚度k0可以直接用式(4)计算得到,此时k0=7.235×109N/m.而对于变刚度裂缝梁,取ζ=5,将其代入式(10)中计算得kc=3.618×1010N/m.将λ=0.3代入式(9)中,可得到变刚度裂缝梁中呼吸裂缝的临界张开弯矩M0=2.293×105N/m. 对3种梁分别进行车桥耦合振动分析。当车辆荷载为26 250 kg(车桥的质量比为0.18),路面不平顺等级为一般时,分别得到3种梁在车辆荷载作用下梁跨中的挠度随时间变化关系,如图7所示。 图7 不同裂缝模型跨中挠度响应对比图 Fig.7 Comparison of the deflection response in middle span of different crack models 对比3条曲线可得,3种梁跨中挠度动态变化的趋势是相同的,开裂梁的跨中挠度比完整梁的要大。与完整梁相比,定刚度裂缝梁和变刚度裂缝梁计算得到的跨中最大挠度分别增大了23.1%和16.2%.这种差异表明呼吸裂缝闭合效应对梁体的整体性能有很明显的影响。在相同的损伤程度下,如果采用定刚度模拟裂缝损伤,会使得模拟得到的响应偏大。 当车辆的质量分别为8 750 kg,17 500 kg和26 250 kg,即车桥质量比mV/mB分别为0.06,0.12,0.18时,对开裂钢筋混凝土变刚度裂缝梁进行了车桥耦合振动分析。 在计算结果中提取移动车辆在简支梁上行走引起的呼吸裂缝截面处刚度的变化图,如图8所示。 图8 呼吸裂缝所在截面刚度与车辆位置关系图 Fig.8 Relationship between the section stiffness and the position of the vehicle 由图8中可见,车辆越接近跨中,呼吸裂缝所在截面的刚度越小。移动车辆荷载作用下开裂截面刚度变化曲线呈U形。当车辆荷载移动一段距离后,跨中弯矩达到临界弯矩M0值时,呼吸裂缝所在截面刚度出现一个陡降区。当车辆荷载的质量较小时,可以看到U形曲线变得非常不平滑,整个过程刚度值变化剧烈。 将计算得到的梁跨中位置的加速度谱进行快速傅里叶变换,对频谱进行截尾处理得到的频谱图如图9所示。为了对比,对17 500 kg车辆荷载(mV/mB=0.12)作用下完整梁、定刚度裂缝梁的跨中加速度谱也进行相同的处理,如图10所示。对比图9和图10,可以发现,在3种梁的跨中加速度谱中均得到了简支梁振动的一阶频率。相对于完整梁,名义损伤比为0.3时,定刚度裂缝梁的一阶频率值降低了8%,而变刚度裂缝梁的一阶频率值降低了4%.但是变刚度裂缝梁的频谱图中除了包含梁体的一阶振动频率外,还出现了小于一阶频率的分量,这些分量的值大约是梁体一阶频率的1/2和1/8,这是非线性振动中典型的亚谐振动现象。这种差异表明,呼吸裂缝的闭合效应使得开裂钢筋混凝土的振动特性更加丰富。 图9 不同车重作用下变刚度裂缝模型梁振动频谱图 Fig.9 Vibration spectrum Cracked reinforced concrete beam under different vehicle weights 图10 完整梁和定刚度裂缝梁振动频谱图 Fig.10 Vibration spectrum of the undamaged beam and the fixed stiffness crack model beam 对比图9中的(e),(f)和图10中的(a)图可以发现,当车辆荷载变大时,梁体亚谐振动的1/2阶分量幅值逐渐变小,而1/8阶分量幅值逐渐变大。说明车辆荷载对开裂梁振动是有显著影响。 1) 通过设置裂缝的传力宽度阈值,可以简单有效地表示呼吸裂缝闭合效应对裂缝所在截面刚度的影响。 2) 开裂后钢筋混凝土梁的动挠度将变大。在裂缝名义损伤比相同的情况下,定刚度裂缝模型梁计算得到的挠度值,要比考虑呼吸裂缝的闭合效应后的变刚度裂缝模型梁的挠度大30%,这种差异必须要引起重视。 3) 整个行驶区间内,呼吸裂缝刚度呈现“U”形变化。车辆在行进过程中,呼吸裂缝刚度存在一个急剧变化的阶段。 4) 当考虑呼吸裂缝的闭合效应时,车辆荷载激励下的开裂钢筋混凝土梁会发生亚谐振动。车辆荷载的大小与1/2,1/8倍频的亚谐振动幅值变化存在相关性。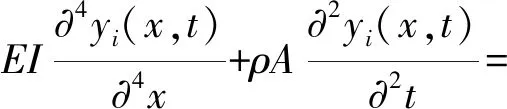
y2(L,t)=0,y"2(L,t)=0 .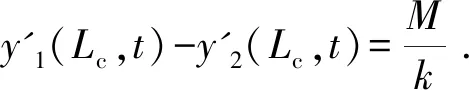
2.2 车辆模型
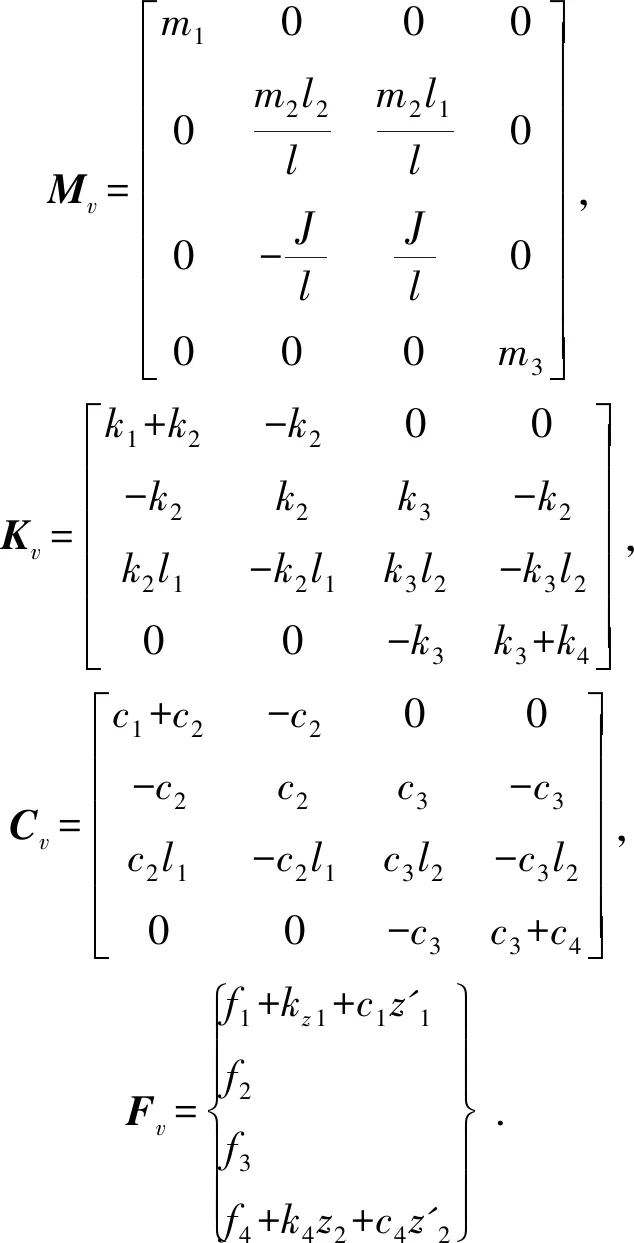
2.3 路面不平顺
2.4 车桥耦合振动分析
3 算例分析
3.1 模型主要参数
3.2 采用不同呼吸裂缝模型的比较分析
3.3 不同车重对开裂钢混梁振动特性影响
4 结论
