带钢板暗支撑混凝土核心筒有效翼缘宽度分析
2019-05-29胡张齐汪梦甫罗丹
胡张齐 汪梦甫 罗丹


摘 要:利用有限元软件ABAQUS对带钢板暗支撑混凝土核心筒进行模拟,计算结果与试验结果吻合较好.在此基础上分析了不同荷载步(位移角)、高宽比、连梁因素、角柱和暗柱型钢率以及暗支撑配钢率对剪力滞后效应的影响,得出了各工况下有效翼缘宽度(最不利情况).结果表明,有效翼缘宽度be在核心筒接近屈服时最小.剪力滞后效应随着高宽比的增加而减弱,be增加.连梁纵筋率及配板率对be的影响甚小,跨高比影响较大,be与之呈正相关.轴压比增大时,有效翼缘宽度增加.角柱型钢率、暗支撑配钢率及暗柱型钢率亦能影响有效翼缘宽度,前两者增加有助于be增加,后者效果较小.
关键词:核心筒;钢板暗支撑;剪力滞后;数值模拟;有效翼缘宽度
中图分类号:TU375 文献标志码:A
Abstract: The concrete core walls with steel plate bracings are simulated by finite element software ABAQUS, and the simulated results are in good agreement with the test results. The effects of loading process,aspect ratio, coupling beam steel ratio,corner column steel ratio,concealed column steel ratio and concealed bracing steel ratio for the shear lag are discussed, and the minimum effective flange width for various conditions is obtained. The results show that the effective flange width be reaches the minimum value when the core wall yields. The shear lag effect weakens as long as the aspect ratio increases, and thus the value of be increases. The reinforcement ratio and steel ratio have little impact on be,but be increases with the effect of span-depth ratio of the coupling beam. The axial load ratio is also helpful for the growth of be. Increasing the steel ratio of the corner column and concealed bracing increases be,but the effect of the concealed column steel ratio is not significant.
Key words:core wall;steel plate concealed bracing;shear lag;numerical simulation;effective flange width
工字形、T形、薄壁箱形結构在受到竖向荷载时,应用等梁理论,翼缘正应力均匀分布,然而实际情况是,翼缘所受正应力与距腹板的距离相关,距离腹板越远端正应力越小,这种现象称为剪力滞后.国内外学者已对该现象进行了大量的研究[1-3],由于上述结构受力复杂,给工程设计带来不便.为方便计算,有效翼缘宽度被提了出来,并广泛应用于T形、工字形、薄壁箱形结构以及组合梁[4]的设计当中,该方法考虑剪力滞后又能应用等梁理论.
对于高层建筑中采用的T形剪力墙、工字形剪力墙及核心筒结构等,同样存在剪力滞后,国内学者从试验[5-7]及有限元[8]两方面分析了核心筒的剪力滞后效应.然而分析的内容仅限于应变方面,实际工程当中,我们更为关心的是其应力分布,核心筒在此方面的研究甚少得见.西安建筑科技大学的史庆轩教授等首次利用有限元软件ABAQUS对T形剪力墙的翼缘应力分布进行了相关分析,并给出了有效翼缘宽度设计建议值[9].
我国规范对于核心筒的相关规定较少,通常是参照剪力墙的设计方法进行相关设计[10],然而核心筒是空间结构,受力相对复杂,直接采用剪力墙的方法进行设计必然存在一些问题.仍需对其进行进一步的研究,特别是在考虑空间受力时,需要研究核心筒翼缘的应力分布状况.
为改善剪力墙及核心筒的抗震性能,学者们进行了一系列的研究[11-16].本文基于已有的研究成果[14-18],提出了带钢板暗支撑混凝土核心筒,并完成了3个试验,结合试验结果,利用有限元软件ABAQUS对其进行分析,研究了不同加载步、高宽比、连梁配板率(钢板与连梁截面积之比)、约束边缘构件型钢率以及暗支撑配钢率等对核心筒剪力滞后以及有效翼缘宽度的影响.
1 模型验证
1.1 试验基础
本文中3个带钢板暗支撑核心筒编号分别为HCW1、HCW2和HCW3,配筋如图1所示(HCW2).其中HCW1为3层,高1 995 mm,HCW2及HCW3为4层,高2 660 mm,试验轴压比分别为0.1、0.1和0.2.HCW1和HCW2的不同仅在于高宽比,HCW2和HCW3不同仅在于轴压比,3个试件连梁跨高比均为1.67.3组混凝土立方体平均抗压强度分别为36.6 MPa、33.5 MPa和31.2 MPa.钢筋力学性能如表1所示[19].
试验结果显示,轴压比同为0.1,但高宽比不同的试件HCW1和HCW2,前者斜裂缝较多,后者水平裂缝分布较广,说明高宽比较大时破坏形态更趋于弯曲破坏,其他性能指标也显示,核心筒高宽比较大时,更有利于抗震.对比轴压比不同的试件HCW2和HCW3,后者在连梁出现明显的塑性铰之前,工字钢及外层钢筋鼓出,表现为明显的屈曲,附近混凝土压溃,且斜裂缝分布相对较广,HCW3虽承载力及刚度较大,但变形能力及延性均有下降.
1.2 有限元验证
为验证本文有限元模型的合理性,采用ABAQUS对本文3个试件进行模拟.混凝土采用C3D8R单元,钢筋采用T3D2单元,型钢、连梁钢板及暗支撑均采用S4R单元.型钢及钢筋本构采用双折线模型,泊松比取0.3,钢筋及铁丝弹性模量取2.05×1011 MPa,钢板弹性模量取2.1×1011 MPa,其他力学指标如表1所示.本文混凝土本构采用我国《混凝土结构设计规范》(GB50010—2010)本构,相关参数见表2.混凝土加载板与核心筒顶部平面采用绑定约束(tie),钢筋网及型钢骨架嵌入(embedded)到混凝土当中.在加载板顶部加均匀压应力以模拟轴压作用,最后于加载板中部施加水平荷载,全位移控制,单调加载.网格划分如图2所示(HCW2).
(a)混凝土 (b)型钢骨架
表3及图3、图4分别为试验与有限元分析结果对比,包括峰值荷载、峰值位移、力-位移曲线以及裂缝分布图.由于模拟与试验加载方式的不同(试验采用低周往復加载,本文模拟采用单调加载方式),因此受拉损伤与实际情况虽在一定程度吻合,但仍有区别,如图4所示.
(a) HCW2裂缝分布 (b) HCW2受拉损伤
2 剪力滞后效应分析
由模拟结果可得到HCW2的应力云图(图5)及正应力矢量云图(图6).由图5和图6可以看出,核心筒角部应力最大,远离腹板处较小,剪力滞后明显.产生这种现象的原因在于,在水平荷载作用下,翼缘在其自身平面内存在剪切变形,剪力流从腹板向翼缘传递的过程中,通过墙体的剪切变形从两侧向中间逐渐传递,而由于剪力墙平面外刚度小,致使翼缘中间部位的正应变及正应力小于两侧.
3 有效翼缘宽度分析
3.1 加载位移角
由文献[8-9],底部剪力滞后效应最为严重,并延墙肢高度方向减弱,结合底部混凝土压应力最大的特性,本文选取墙肢底部处的正应力作为研究对象.参照文献[9]的方法,提取混凝土单元形心处的应力,因核心筒为对称结构,本文仅取左部墙肢为研究对象,HCW2(模拟)于不同位移角时底部混凝土正应力分布图如图7所示(本文试验加载位移角为0.05%,0.125%,0.25%,0.5%,0.75%,1%,…).
由图7可知,随着加载位移角的增大,应力分布曲线倾斜角度先增大后减小,位移角为1%时,翼缘最大压应力位置不再是角部混凝土单元,原因在于此处的混凝土已超过峰值应变,应力开始呈下降趋势,压应力最大位置向翼缘中部发生转移.
根据等效应力原则,核心筒的有效翼缘宽度可按式(1)计算:
式中:bf为翼缘宽度(本文为500 mm),σ0为翼缘靠近腹板处应力.有效翼缘宽度与位移角的关系如图8所示.
由图8可以看出,有效翼缘宽度出现两个极小值点,对应的位移角θ分别为0.180%和0.761%.产生这种现象的原因在于,核心筒底部混凝凝土所受压应力由加载板和腹板共同传递,其中腹板通过剪切变形传递应力,而除了轴压力外加载板还可通过与顶部墙肢的接触传递弯矩而产压应力(弯矩产生的压应力分布均匀).初始阶段,压应力主要源自轴压,墙肢混凝土应力分布均匀,有效翼缘宽度大,而后由于水平位移的增加,剪切变形增大,剪力滞后效应明显,至位移角0.180%时,be第一次达到极小值.随着位移角的继续增加,筒体出现偏心受压,顶部墙肢混凝土应力由受压转为受拉(如图5),且越靠近腹板处受拉作用越明显,进而影响底部混凝土压应力分布,致使剪力滞后效应在θ超过0.180%后有所缓解,be由此增大.该拉应力的相对作用先增大后减小,be达到极大值后再次下降.至θ为0.761%时,角部混凝土单元达到峰值压应力(第二极小值点),最大压应力位置开始发生转移,be再次开始增大.位移角0.180%和0.761%时对应的be分别为349.7 mm和359.0 mm,相对有效翼缘宽度η(有效翼缘宽度与实际翼缘宽度比值)分别为0.699和0.718.因θ为0.761%时早已屈服,对应的水平力接近峰值,位移角0.180%时,be更小,且此时核心筒接近屈服,于工程设计而言,为最不利情况.故而本文将该点的be作为研究对象(后文有效翼缘宽度均表示该点be).
3.2 高宽比
高宽比(剪跨比)会影响核心筒的破坏形态,当高宽比小时,核心筒趋于剪切破坏,反之,当高宽比较大时趋于弯曲破坏.建立高宽比λ = 1.33(HCW1)、1.77(HCW2)、2.21、2.66(对应层数分别为3~6层)的有限元模型,以分析高宽比对剪力滞后及有效翼缘宽度的影响.
由图9,高宽比增大时,曲线稍显平滑(本文模拟时高宽比变化区间不大,因此由于高宽比的影响导致剪力滞后效应的变化不甚明显),剪力滞后效应减小,对应的有效翼缘宽度如表4所示.
由表4可知,核心筒有效翼缘宽度随高宽比的增加而增加,空间效应随之提高.产生这种现象的原因在于,高宽比越大的核心筒,通过加载板传递弯矩而产生的应力所占比例增加,剪力滞后效应降低.
3.3 连梁因素
3.3.1 连梁配板率
连梁配板率τ表示连梁钢板截面积与连梁截面积的比值.2015年,王义俊等分析了连梁配板率等对剪力墙抗震性能的影响,分析表明连梁配板率的增加能提高剪力墙的峰值承载力[20].为研究连梁配板率对核心筒有效翼缘宽度的影响,本文在HCW2的基础上建立4个τ分别为1%、2%(HCW2)、3%和4%的模型,最不利情况正应力分布如图10所示.
从图10中可看出,当连梁配板率在2%~4%时,曲线几乎重合,而当配板率为1%时,应力值略小.有效翼缘宽度计算值见表5.
由表5对比可知,随着连梁配板率增加,有效翼缘宽度略有减小,但大体相当.
3.3.2 连梁纵筋率
连梁纵筋率影响承载力、延性及破坏形态[7].为研究连梁纵筋率对核心筒有效翼缘宽度的影响,本文在HCW2的基础上分析连梁纵筋直径分别为6 mm(HCW2模型)、8 mm和10 mm,纵筋率ρ分别为0.25%、0.45%和0.75%的3个模型,正应力分布如图11所示.
由图11可知,连梁纵筋率增大对于剪力滞后效应的影响并不明显,有效翼缘宽度计算结果如表6所示.从表6可看出,连梁纵筋率增大,核心筒的有效翼缘宽度增加,对应的位移角略有提前,但作用不明显.
3.3.3 连梁跨高比
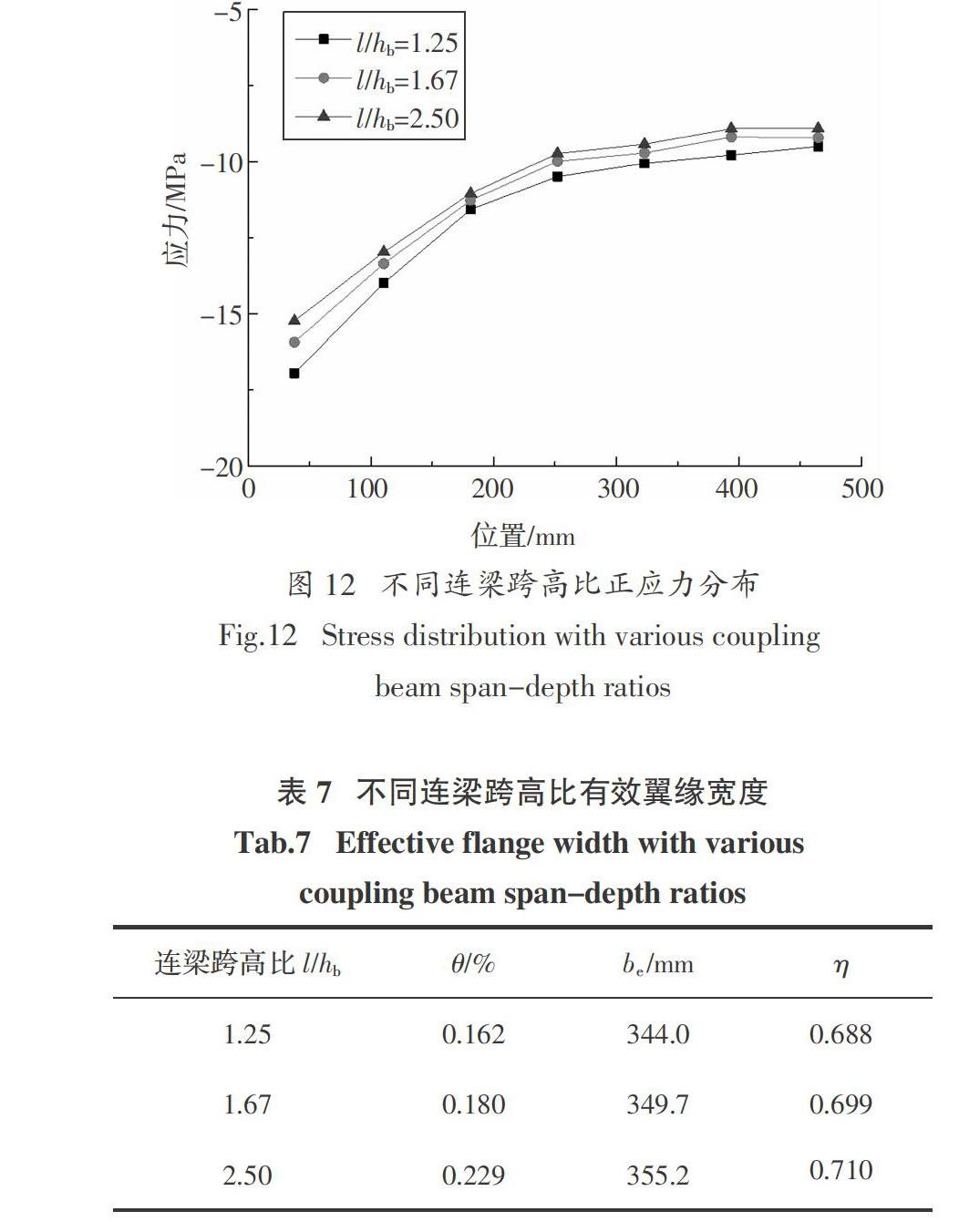
为研究连梁跨高比对剪力滞后效应及有效翼缘宽度的影响,建立连梁跨高比l/hb = 2.50、1.67(HCW2)和1.25的模型(对应的连梁截面高度分别为200 mm、300 mm和400 mm),对其进行单向加载分析,正应力分布图及有效翼缘宽度分别如图12和表7所示.
由图12和表7可知,连梁跨高比增大会降低核心筒的剪力滞后效应,相应的有效翼缘宽度增加,对应的位移角推后.
由图9~图12、表5~表7可知,连梁配板率及纵筋率对有效翼缘宽度影响不大,但连梁跨高比的增加却会使be增加.本文认为纵筋率和配板率的变化虽会影响核心筒的承载力及破坏形态,但其作用主要表现在峰值之后,前期对于核心筒刚度的影响较小,相较而言,当改变连梁跨高比时,则会影响其刚度的变化,l/hb越小,腹板刚度越大,通过剪切变形传递压应力所占比例增加,剪力滞后效应增大,故而be减小.
3.4 轴压比轴压比影响着核心筒的承载力及破坏形
态[21-22].当轴压比较高时,峰值荷载增大,对应的位移角提前,延性下降.本节分析了轴压比n为0.1、0.2、0.3和0.4的4个模型剪力滞后效应及有效翼缘宽度.最不利情况时应力分布如图13所示,对应的有效翼缘宽度如表8所示.
由图13和表8可知,增加轴压比使翼缘正应力增大,剪力滞后效应降低,有效翼缘宽度增大.分析其原因为,在加载过程当中,核心筒出现偏心受压,致使受压翼缘顶部出现混凝土受拉区,随着轴压比的增大,该受拉区减小,如图14所示,进而使实际剪跨比增加,由弯矩而产生的应力所占比例增大(本文3.2节).
3.5 约束边缘构件型钢率
我国规范[10]对核心筒的约束边缘构件提出了比剪力墙更高的设置要求,以期更好地发挥其抗侧能力.本文核心筒中的角部约束边缘构件(角柱)及洞口约束边缘构件(暗柱)当中分别安放了十字型钢和工字型钢,型钢截面积分别为351 mm2和210 mm2,型钢率分别为2.08%和2.33%(型钢截面积与约束边缘构件面积的比值),本节仍以HCW2为基础研究约束边缘构件型钢率(仅改变钢板厚度)对有效翼緣宽度的影响
3.5.1 角柱型钢4个模型的角柱型钢率τJ分别为1.05%、2.08%、3.08%和4.05%,正应力分布如图15所示.
由图15可知,角柱型钢率的改变对剪力滞后效应作用明显,τJ越大,正应力越小,应力分布曲线越平滑,剪力滞后效应减弱.表9为对应的有效翼缘宽度.
3.5.2 暗柱型钢率
4个模型的暗柱型钢率τA分别为1.17%、2.33%、3.50%和4.67%,正应力分布如图16所示.
由图16可知,暗柱型钢率的变化对剪力滞后效应影响很小,应力分布曲线几乎重合,有效翼缘宽度如表10所示.
由图15和图16、表9和表10可知,暗柱型钢率对应力分布及有效翼缘宽度的影响甚小,但角柱型钢率效果明显,τJ增加,有效翼缘宽度增大,对应的位移角稍稍减小.笔者对于这种现象的解释为,角柱型钢率的增加能在更大程度上分担翼缘混凝土所承受弯矩,使翼缘混凝土所受压应力减小,而该作用由于是通过剪力传递,使得远离腹板端应力削减效果变弱,导致剪力滞后效应减小,有效翼缘宽度增加.而对于暗柱,增加工字钢型钢率,虽也能分担部分弯矩作用,但受压翼缘暗柱当中的型钢为弱轴参与受力,效果不明显.位于腹板洞口两侧的(暗柱)工字钢,一侧受压另一侧受拉,受压工字钢能减小暗柱混凝土所受压应力但无法影响到受压翼缘,腹板受拉工字钢对受压翼缘应力分布同样影响甚微.
3.6 墙肢暗支撑配钢率
墙肢当中设置暗支撑配钢率τB表示,暗支撑截面积与墙肢截面积的比值.本文试验中钢板暗支撑的配钢率为0.8%,在此基础上建立τB为0.4%、0.8%(HCW2)、1.2%和1.6%的4个模型,正应力分布如图17所示.
由图17可知,墙肢暗支撑配钢率提高,使应力分布曲线平滑,剪力滞后效应减弱.对应的有效翼缘宽度如表11所示.
由表11可知,暗支撑配钢率的提高有助于增加核心筒有效翼缘宽度,对应位移角增大.本文认为,墙肢暗支撑配钢率的增加虽不能直接影响翼缘混凝土的应力分布,但能增强结构的整体性,有利于角柱型钢发挥其抗弯作用,使翼缘混凝土应力分布均匀,从而增加有效翼缘宽度.
4 结 论
利用有限元软件ABAQUS对本文3个带钢板暗支撑混凝土核心筒模拟,分析结果与试验吻合较好,并在此基础上分析了不同高宽比、连梁因素、轴压比、约束边缘构件型钢率以及暗支撑配钢率对剪力滞后及有效翼缘宽度的影响,结论如下:
1)有效翼缘宽度与加载位移角有关,从对HCW2试件的模拟结果来看,be出现两次极小值点,对应的位移角θ分别为0.180%和0.761%,be分别为349.7 mm和359.0 mm,相对有效翼缘宽度η(有效翼缘宽度与实际翼缘宽度比值)分别为0.699和0.718,由于θ为0.180%时,有效翼缘宽度较小,且接近屈服阶段,故而将该处be作为研究对象更有意义.
2)高宽较比大的核心筒剪力滞后效应减小,有效翼缘宽度大,且对应的位移角推后.
3)连梁参数的不同也能影响最小有效翼缘宽度,包括配板率、纵筋率及跨高比.前两者对be的影响较小,计算值几乎一致;连梁跨高比l/hb影响较大,与be呈正相关,即,l/hb越大be越大.
4)轴压比增大,剪力滞后效应减弱,有效翼缘宽度增加.
5)约束边缘构件包括角柱和暗柱,其中角柱型钢率τJ的变化对有效翼缘宽度的影响较大,τJ增加使有效翼缘宽度增加;暗柱型钢率对be的影响较小.
6)暗支撑配钢率τB虽不能直接影响应力分布,但增加τB能增强核心筒整体性,有利于角柱型钢发挥其抗弯作用,有效翼缘宽度增加.
参考文献
[1] 甘亚南,石飞停.梯形箱梁剪力滞后效应的精细化分析[J]. 计算力学学报,2014,31(3):351—356.
GAN Y N,SHI F T. The delicate analysis of shear lag effect on trapezoidal box girder[J]. Chinese Journal of Computational Mechanics,2014,31(3):351—356.(In Chinese)
[2] 韦成龙,李斌,曾庆元. 变截面连续箱梁桥剪力滞及剪切变形双重效应分析的传递矩阵法[J].工程力学,2008,25(9):111—117.
WEI C L,LI B,ZENG Q Y. Transfer matrix method considering both shear lag and shear deformation effects in non-uniform continuous box girder[J]. Engineering Mechanics,2008,25(9):111—117.(In Chinese)
[3] SUN F F ,BURSI O S,ASCE A M. Displacement-based and two-field mixed variational formulations for composite beams with shear lag[J]. Journal of Engineering Mechanics,2005,131(2):199—210.
[4] 聂建国,王宇航.钢-混凝土组合梁混凝土翼板开洞截面有效翼缘宽度分析[J].建筑结构,2010,40(4):72—75.
NIE J G,WANG Y H. Analysis of effective flange width on composite steel-concrete beams with openings in concrete slab[J]. Building Structure,2010,40(4):72—75.(In Chinese)
[5] 呂西林,李俊兰.钢筋混凝土核心筒体抗震性能试验研究[J].地震工程与工程振动,2002,22(3):42—50.
X L,LI J L. Seismic behavior of reinforced concrete core walls subjected to cyclic loading[J]. Earthquake Engineering and Engineering Vibration,2002,22(3):42—50.(In Chinese)
[6] 杜修力,贾鹏,赵均.不同连梁跨高比混凝土核心筒抗震性能试验研究[J].建筑结构学报,2009,30(S):5—9.
DU X L,JIA P,ZHAO J. Experimental study on seismic behavior of reinforced concrete core walls with various span-depth ratio of coupling beam[J]. Journal of Building Structures,2009,30(S):5—9. (In Chinese)
[7] 史庆轩,侯炜,刘飞,等. 钢筋混凝土核心筒抗震性能试验研究[J]. 建筑结构学报,2011,32(10):119—129.
SHI Q X,HOU W,LIU F,et al. Experiment on seismic behavior of reinforced concrete core walls under low cycle reversed loading[J]. Journal of Building Structures, 2011, 32(10): 119—129. (In Chinese)
[8] 汪梦甫,陈兵.带混合暗支撑的钢筋混凝土剪力滞后效应分析[J].力学季刊,2015,36(3):493-501.
WANG M F,CHEN B. Analysis of the effect of shear lag of reinforce concrete core walls with mixed concealed bracings [J].Chinese Quarterly of Mechanics, 2015, 36(3): 493—501. (In Chinese)
[9] 史庆轩,王斌,郑晓龙,等.T形截面带翼缘剪力墙剪滞效应分析及有效翼缘宽度讨论[J]. 建筑结构,2014,44(22):67—71.
SHI Q X,WANG B,ZHENG X L,et al. Shear lag effect analysis and effective flange width study of the T-shaped shear wall with flange[J]. Building Structure,2014,44(22):67—71.(In Chinese)
[10] JGJ3—2010 高层建筑混凝土结构技术规程[S].北京:中国建筑工业出版社,2011:77—106.
JGJ3—2010 Technical specification for concrete structures of tall buiding[S]. Beijing:China Architecture and Building Press,2011:77—106.(In Chinese)
[11] 曹万林,黄选明,卢智成,等. 钢筋混凝土带暗支撑核心筒体抗震性能试验研究[J].地震工程与工程振动,2005,2(3):81—86.
CAO W L,HUANG X M,LU Z C,et al. Experimental study on seismic behavior of reinforced concrete core walls with concealed bracings[J]. Earthquake Engineering and Engineering Vibration,2005,2(3):81—86.(In Chinese)
[12] 董宏英,耿海霞,张建伟,等.钢管混凝土叠合柱边框组合核心筒抗震性能试验研究[J]. 北京工业大学学报(自然科学版),2011,37(11):1720—1728.
DONG H Y,GENG H X,ZHANG J W,et al.Experimental study on seismic behavior of composite core walls with Steel tube-reinforced concrete columns[J]. Journal of Beijing University of Technology(Natural Sciences),2011,37(11):1720—1728.(In Chinese)
[13] 張建伟,耿海霞,曹万林,等. 叠合柱边框内藏钢桁架带洞口组合核心筒抗震性能研究[J]. 北京工业大学学报(自然科学版),2011,37(11):1668—1676.
ZHANG J W,GENG H X,CAO W L,et al. Seismic performance of composite core walls with steel tube-reinforced concrete columns and concealed steel truss[J]. Journal of Beijing University of Technology(Natural Sciences),2011,37(11):1668—1676. (In Chinese)
[14] 宋兴禹,汪梦甫. 高阻尼混凝土混合暗支撑双肢剪力墙试验研究[J]. 湖南大学学报(自然科学版),2013,40(4):15—19.
SONG X Y,WANG M F. Experimental study on seismic performance of high damping concrete coupled shear wall with enhanced concealed bracings[J]. Journal of Hunan University(Natural Sciences),2013,40(4):15—19. (In Chinese)
[15] 汪梦甫,宋兴禹. 小高跨比连梁混合暗支撑高阻尼混凝土联肢剪力墙试验研究[J]. 地震工程与工程振动,2013,33(3):125—132.
WANG M F,SONG X Y. Experimental study on seismic performance of high damping concrete coupled shear wall with mixed concealed bracings and coupling beams of small span-depth ratios [J]. Earthquake Engineering and Engineering Vibration,2013,33(3):125—132. (In Chinese)
[16] 汪梦甫,王义俊. 高阻尼混凝土带钢板暗支撑双肢剪力墙抗震性能试验研究[J].工程力学,2017,34(1):204—212.
WANG M F,WANG Y J. Experimental study on seismic performance of high damping concrete coupled shear walls with steel plate concealed bracings[J]. Engineering Mechanics,2017,34(1):204—212.(In Chinese)
[17] LAM W Y. Plate-reinforced composite coupling beams:experimental and numerical studies[D]. Hong Kong:The University of Hong Kong,2006:10—94.
[18] 汪梦甫,邹同球. 带暗支撑预制叠合剪力墙抗震性能试验研究[J]. 湖南大学学报(自然科学版),2017,44(1):54—64.
WANG M F,ZOU T Q. Experimental study on seismic behavior of precast composite shear wall with concealed bracing[J]. Journal of Hunan University (Natural Sciences),2017,44(1):54—64.(In Chinese)
[19] 汪梦甫,胡张齐,罗丹.不同高宽比带钢板暗支撑高阻尼混凝土核心筒抗震性能研究[J].地震工程与工程振动,2018,38(3):1—11.
WANG M F,HU Z Q,LUO D. Study on seismic performance of high damping concrete core walls with Steel plate concealed bracings of different aspect ratio[J]. Earthquake Engineering and Engineering Vibration,2018,38(3):1—11. (In Chinese)
[20] 王義俊,汪梦甫. 高阻尼混凝土钢板暗支撑双肢剪力墙数值分析[J]. 湖南大学学报(自然科学版),2015,42(5):14—20.
WANG Y J,WANG M F. Numerical simulation of high damping concrete coupled shear walls with steel plate concealed bracing[J]. Journal of Hunan University (Natural Sciences),2015,42(5):14—20.(In Chinese)
[21] 吕西林,李俊兰. 钢筋混凝土核心筒体抗震性能试验研究[J].地震工程与工程振动,2002,22(3):42—50.
X L,LI J L. Seismic behavior of reinforced concrete core walls subjected to cyclic loading[J]. Earthquake Engineering and Engineering Vibration,2002,22(3):42—50.(In Chinese)
[22] 贾鹏,杜修力,赵均. 不同轴压比钢筋混凝土核心筒抗震性能[J].北京工业大学学报(自然科学版),2009,35(1):63—69.
JIA P,DU X L,ZHAO J. Seismic behavior of reinforced concrete core wall under different axial load ratio[J]. Journal of Beijing University of Technology(Natural Sciences),2009,35(1):63—69. (In Chinese)
