港口起重机钢轨选型检算方法探讨
2019-05-29廖二全张光磊杨洪祥
廖二全,张光磊,杨洪祥
(1.中交第一航务工程勘察设计院有限公司,天津 300222;2.唐山港集团股份有限公司,河北 唐山 063600)
引 言
随着港口经济的飞速发展,港口起重机呈现大型化、作业高速化的发展趋势,随之港口起重机安全问题受到高度重视,其中由于起重机钢轨选型不当,引起的钢轨断裂等安全问题也受到了关注。起重机钢轨选型合理是防治钢轨断裂的前提[1-3],目前港口起重机钢轨选型检算尚无相关规范及标准,一般采用参考对比法,该方法受人为因素影响较大,易出现偏差,实际应用中具有一定的局限性。因此提出一种港口起重机钢轨选型合理性检算方法具有一定的必要性和工程应用价值。
1 港口起重机钢轨选型检算分析
轨道钢轨接触疲劳强度是钢轨表面能否满足使用要求的重要判定依据,轨道动载强度是钢轨整体强度能否达到使用要求的重要判定依据[4]。因此通过分析轨道钢轨接触疲劳强度及动载强度可以有效判定钢轨选型是否合理。目前缺少接触疲劳强度及动强度的计算方法,因此本节将依据轮轨接触理论,推导出钢轨的许用接触压力公式,用于钢轨接触疲劳强度分析;依据均匀连续弹性基础理论及力的独立作用线性叠加原理推导出动载强度校核公式用于钢轨强度分析。
1.1 钢轨接触疲劳强度检算分析
根据轮轨 Hertz[5]接触理论,轮轨接触可用Carter[6]二维滚动接触模型表示,轮轨接触斑为狭长的椭圆,如图1所示。
假设起重机轮轨接触满足 Hertz接触理论条件,则轮轨接触斑上的法向压力分布[7]可用式(1)表示:

式中:x、y分别表示局部的纵向和横向坐标;a、b分别表示椭圆接触斑的短半轴和长半轴长度;p0为接触斑内轮轨作用的最大法向力。

图1 接触斑及轮轨接触二维滚动接触模型
钢轨与车轮的最大接触压力[8-9]为:
式中:p为轮轨接触斑上的总压力。
假设钢轨的屈服强度为σ轨,安全系数为K轨,则钢轨的容许应力为:

假设轮轨接触斑内最大压力的接触面积为S轮轨,则钢轨的允许最大接触压力为:

钢轨的允许接触轮压为:

由于接触面积S轮轨尚无相应公式计算,因此钢轨许用接触压力不能直接计算求得。
与钢轨的允许接触轮压计算方法一样,车轮的许用接触轮压为:

假设钢轨的安全系数与车轮的安全系数取值相同,则有:

允许轮压的计算公式采用:
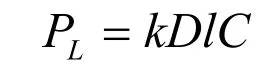
式中:k为车轮或滚轮的许用比压,N/mm2;D为车轮或滚轮的踏面直径,mm;l为车轮或滚轮与轨道承压面的有效接触宽度,mm;C为计算系数,C=C1C2,C1为转速系数,C2为车轮所在机构的工作级别系数。
因此,可以求得钢轨的许用接触压力为:
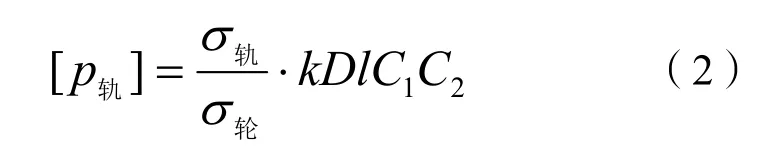
1.2 钢轨强度检算分析
钢轨可视为连续弹性支承的等截面无限长梁,钢轨基础的竖向位移与其反力成线性关系;车轮作用在轨道上的荷载符合力的独立作用原理,即在车轮系作用下钢轨的应力、应变等于各独立车轮作用下应力、应变的代数和。
单个车轮作用下,均匀连续弹性基础上的钢轨挠曲曲线如图2所示。
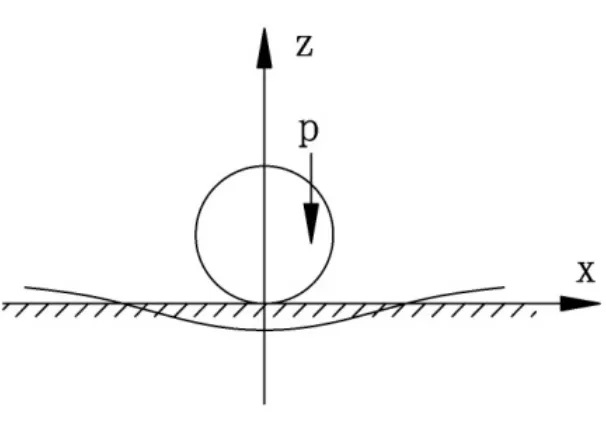
图2 单轮作用的钢轨挠曲曲线示意
挠曲曲线的微分方程可表示为:

式中:M为钢轨弯矩,N·mm;E为钢轨弹性模量,N/mm2;Ix为钢轨截面对水平中性轴的惯性矩,cm4。
根据文克尔(E.Winkler)的相关假设,推导得到:

式中:k为钢轨基础与钢轨的刚比系数。k可通过下式求得:

通过求解得到钢轨在单车轮静轮压作用下的弯矩M0静轮可按下式计算:

式中:P0为单个车轮静载压力,N;μ0为均匀连续弹性基础上无限长梁的弯矩影响系数。
根据均匀连续弹性基础理论及力的独立作用线性叠加原理,钢轨在轮系作用下的静弯矩M0轮系可按下式计算:

在对钢轨强度进行选型计算时,应当考虑相关的运动荷载,车轮动荷载作用下的钢轨弯矩Md可按下式计算:

式中:α为大车行驶速度系数,可按α=0.6v/100取值,v为大车行驶速度,km/h;β为偏载系数,直线轨道取0。
钢轨在车轮动载作用下,其边缘的最大可能动弯应力可按下式计算。
1)钢轨的轨头边缘最大可能受到的动弯应力

式中:f为轨道横向力水平系数,直线轨道取1.25;W头为钢轨上部断面系数,cm4。
2)钢轨的轨底边缘最大可能受到的动弯应力

式中:W底为钢轨下部断面系数,cm4。
另外还应考虑温度应力的影响,温度应力可按下式计算:

式中:στ为温度应力,MPa;Δt为当地最高轨温或最低轨温与钢轨安装时锁定轨温之差,℃。
车轮在钢轨行驶时,钢轨的动载强度校核,可按如下公式计算:

式中:σs为钢轨的屈服强度;K为安全系数,建议取值 1.5~2.5,养护条件较好的明轨可取较小值,养护条件较差的暗轨建议取较大值。
通过以上计算公式可逆向检算钢轨强度选型是否合理。
2 选型举例
本节将以某港口一期工程所选Qu80钢轨以及二期所选 Qu100钢轨作为研究对象进行了钢轨的选型检算,检算结果与两期工程钢轨实际运行状况进行对比,验证该检算方法的是否具有可操作性及应用价值。
2.1 设计条件
某港口起重机的轨距为33 m,基距为8.6 m,轮数为4×4=16个,单腿轮间距为1.1 m+1.4 m+1.1 m,单腿轮系布置如图4所示。最大压为320 kN,运行速度为 160 m/min,车轮工作级别 M8,车轮直径800 mm,车轮材质 42CrMo,屈服强度取值930 MPa。
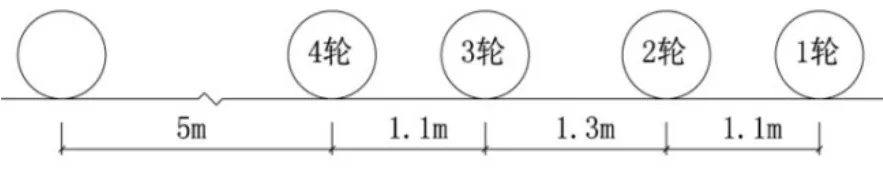
图3 起重机大车单腿轮系布置
2.2 钢轨接触疲劳强度检算
在一期工程中,钢轨选用QU80;二期工程中,钢轨选用QU100。材质均选用U71Mn,热处理后抗拉强度不小于1 180 MPa时,屈服强度取值800 MPa。钢轨全长范围内设钢轨支座,支座间距500 mm。起重机的实际最大轮压为320 kN。
根据计算公式(2)求得,一期选用 QU80钢轨的许用轮压为273 kN,小于起重机的实际最大轮压,因此选用的钢轨的接触疲劳强度不满足要求。二期工程选用QU100钢轨的许用轮压为358 kN,大于起重机的实际最大轮压,因此选用的钢轨的接触疲劳强度满足要求。
2.3 钢轨动强度检算
两期工程所用起重机机型相同,因此 ΣPiμi计算值均相同。由于起重机两腿间距较大,故不考虑相邻腿的轮压影响。而单腿车轮是对称布置,1轮与4轮、2轮与3轮对轨道压应力分别相同,因此计算时仅需考虑轮 1和轮 2的压应力即可。ΣPiμi计算值如表1所示。

表1 ΣPiμi计算值
由以上计算可知,1轮荷载较大,将其作为校验的输入条件,取ΣPiμi=233 kN。
1)QU80钢轨动强度检算
QU80钢轨对水平轴线的惯性力矩为1 530 cm4;钢轨支座刚度取 3×104N/mm;钢轨的弹性模量取2.06×105N/mm2。
根据钢轨动强度检算公式计算,钢轨的动强度检算如下:
根据公式(4)~(8)求得:钢轨基础预钢轨的刚比系数k为0.14770 cm-1,静弯矩M0为3 943.9 kN·cm,动弯矩Md为4 171.0 kN·cm;QU80钢轨上部断面系数为234.86 cm3,下部断面系数为235.95 cm3;钢轨的轨头边缘动弯应力σ头d为222.0 N/mm2,钢轨的底边缘动弯应力σ底d为221.0 N/mm2;设温差△t为 30 ℃,则σt为 73.5 MPa。
钢轨动强度检算带入公式(9)、(10)得:

由以上结果可知,选用QU80钢轨的轨头边缘动弯应力为 295.5 MPa,轨底边缘动弯应力为294.5 MPa,而许用应力为320 MPa,因此选用的钢轨的动强度满足要求。
2)QU100钢轨动强度检算
QU100钢轨对水平轴线的惯性力矩为2 806 cm4;钢轨支座刚度取 3×104N/mm;钢轨的弹性模量取2.06×105N/mm2。
根据钢轨动强度检算公式计算,钢轨的动强度计算过程QU80钢轨动强度检算:
钢轨基础预钢轨的刚比系数k为0.012692 cm-1,其静弯矩M0为 4 589.5 kN·cm,其动弯矩Md为4 853.9 kN·cm;QU100钢轨上部断面系数为380.64 cm3,下部断面系数为367.87 cm3;钢轨的轨头边缘动弯应力σ头d为367.87 cm3,钢轨的底边缘动弯应力σ底d为159.4 N/mm2;设温差△t为30 ℃,则σt为 73.5 MPa。
钢轨动强度检算结果:
由以上结果可知,选用 QU100钢轨的轨头边缘动弯应力为 232.9 MPa,轨底边缘动弯应力为238.4 MPa,而许用应力为320 MPa,因此选用的钢轨的动强度满足要求。
2.4 结果分析
通过以上对钢轨接触疲劳强度以及钢轨动强度的检算可得,一期选用的QU80钢轨可以满足钢轨动强度的要求,但是不能满足钢轨接触疲劳强度的要求,该种情况下易出现表面裂纹、剥离等问题。二期选用的 QU100钢轨可以满足其接触疲劳强度及动强度的要求。
3 结 语
本文依据轮轨接触理论,推导出钢轨的许用接触压力公式,用于钢轨接触疲劳强度分析;依据均匀连续弹性基础理论及力的独立作用线性叠加原理推导出动载强度校核公式,用于钢轨强度分析。并结合工程应用实例检算,检算结果与现场情况一致,验证了该检算方法的可行性。本文提出的港口起重机钢轨选型检算方法是相对合理的,且具有一定的工程应用价值。
