基于简化模型的光伏组件最大功率跟踪仿真

2019-05-29朱显辉董芮麟

安阳工学院学报 2019年2期

张亢，胥良，朱显辉，师楠，董芮麟

（黑龙江科技大学a.电气与控制工程学院；b.工程训练与基础实验中心，哈尔滨150022）

0 前言

随着石化能源的日益枯竭和气候变暖的逐渐加剧，寻找一种可再生的清洁能源已成为全球能源供给领域的共识，能将储量巨大的太阳能转化为电能的光伏发电装置得到了广泛的重视。光伏组件是将光能转换为电能的核心设备，因材料和制造工艺的影响，当前其光电转换效率仅为20%左右[1]。在较低的光电转换效率下，使光伏组件的实际工作点维持在最大功率点附近，是改善光伏输出效率的有效手段，对其进行研究具有较好的理论和现实意义。

国内外专家学者提出了不同的最大功率跟踪策略，具有代表性的主要有：恒定电压法、电导增量法、扰动观察法等[2-3]。恒定电压法是一种简化的最大功率跟踪方法[4-5]，该方法控制简单且易实现[6]，但忽略了辐照度和温度对光伏组件输出特性的影响，在工况变化时不能可靠地跟踪最大功率。电导增量法是基于最大功率点处的电导为0的跟踪策略，控制效果好，稳定度高，但对控制系统的性能和传感器的精度要求也较高[2,7]。扰动观察法通过施加扰动量来判断输出功率的调整方向，其结构简单，被测参数少，也比较容易实现[8]，是目前研究较多、也较为常用的最大功率点跟踪方法[5]。

此外，新型智能算法如粒子群优化算法、神经网络算法、最优梯度优化算法等也在光伏最大功率跟踪中受到了一定关注，但其需要预先给定阈值和权重等参数，很难在工程实践中得到广泛应用[9]。

本文采用扰动观察法作为光伏组件输出特性的最大功率跟踪策略，基于简化的光伏组件输出特性方程，结合典型的Boost升压电路，在Matlab仿真平台上搭建由光伏组件模块、MPPT模块、脉宽调制模块以及升压电路组成的系统模型，给出光伏组件可靠的最大功率跟踪结果，并讨论辐照度和温度对光伏组件输出最大功率点的影响规律，以期为相关的研究提供借鉴。

1 光伏组件数学模型

光伏组件单指数模型的等效拓扑如图1所示。

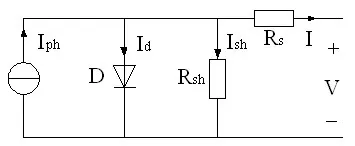
图1中Iph为光生电流（A）；RS为串联电阻（m Ω）；Rsh为并联电阻（kΩ）；Id为流过二极管的电流（A）；Ish为流过并联电阻Rsh的电流（A）；I为组件输出电流（A）；V为组件输出电压（V）。

由基尔霍夫电流定律可知Id可计算为

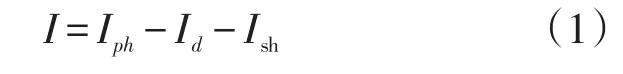
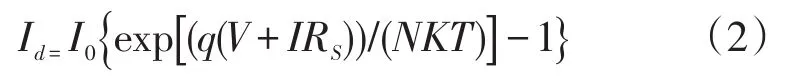
式（2）中：I0为流过二极管的暗电流；q为电子电荷（1.6×10-19C）；N为二极管品质因子；K为玻尔兹曼常数（1.38×10-23J/K）；T为组件的绝对温度（K）。

基于欧姆定律可知，Ish满足

将式（2）、式（3）代入式（1）得

式（4）能较为完善地描述光伏组件的工作原理，已被广泛应用于光伏组件理论分析中。但式（4）为包含五个未知参数Iph、I0、N、Rs、Rsh的超越方程，而且厂家给定的技术手册并不提供上述各参数的具体取值，导致其求解过程比较烦琐，阻碍了在工程实际中的推广应用。

为简化光伏组件输出特性的计算过程，力图在厂商给定短路电流Id、开路电压Vk、最大功率点电流Im、最大功率点电压Vm等参数条件下，计算光伏组件的输出特性曲线。文献[10]给出了以下近似：串联电阻Rs的阻值一般较小，远小于二极管正向导通电阻，故假设Id=Ish，并联电阻Rsh的阻值较大，因此忽略（V+IRs）/Rsh项。

基于上述两点近似，光伏组件的I-V方程可简化为

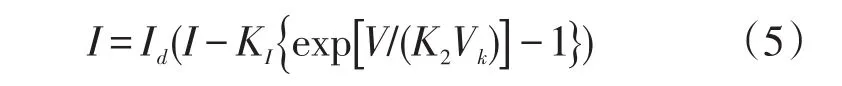
在最大功率点时，将V=Vm，I=Im代入式（5）得

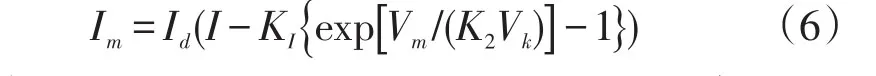
由于在常温条件下exp[Vm/(K2Vk)]远远大于1，因此可忽略式中的“-1”项，解出K1，即

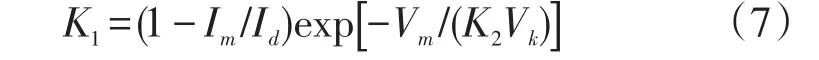
将开路条件I=0，V=Vk代入式（5），并将式（7）代入式（5）得

由于exp(1/K2)远远大于1，忽略式中的“-1”项，解出K2，即

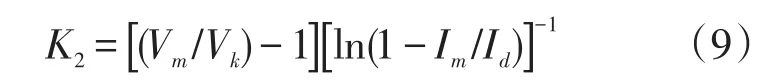
将k1、k2的表达式代入式（5）得到不含未知参数的光伏组件I-V特性方程。

上述得到的光伏组件I-V方程只适用于环境温度25℃，辐照度1000W/m2标准测试环境，在工况变化时，需对上述方程进行如下修正[11]。

式中：Id1，Im1，Vk1，Vm1分别为光伏组件在不同辐照度和温度下的短路电流、最大工作点电流、开路电压、最大工作点电压；△T=T-T0，△G=G-G0，T、G分别为同一时刻光伏组件的实际温度和辐照度，T0、G0分别为标准测试条件下组件的参考温度（25℃）和参考辐照度（1 000 W/m2）；e为自然对数的底数，其值约为2.71828；a、b、c为拟合系数，其典型值推荐为：a=0.0025/℃，b=0.0005/（W/m2），c=0.00288/℃。将式（7）、（9）、（10）代入方程（5）便得到任意工况下光伏组件输出的I-V方程。

2 系统仿真模型的建立

利用前述的简化I-V方程，以TDB125×125-72-P单晶硅光伏组件为例搭建模型，单晶硅光伏组件参数详见文献[12]。

结合上述各模块和Boost电路原理建立了光伏组件最大功率跟踪仿真系统如图2所示。

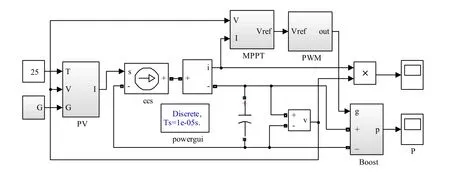
图2 光伏组件最大功率跟踪仿真系统

图2仿真系统中的输入电压、电流通过零阶保持器进行保持之后，与记忆模块中保持的前一次采样信号做差，分别得到电压和功率的变化量，两者相乘的结果输入到Sign函数中，当电压变化量与功率变化量的乘积为正时，Sign函数输出1，否则Sign函数输出-1，并以Sign函数的单位输出与仿真步长的乘积判断最大功率跟踪的调整方法，步长设置为0.001。

脉宽调制模块中引入零阶保持器对MPPT模块输出的参考电压进行保持，并将该值与三角波发生器产生的三角波进行比较，比较结果输入switch转换开关。之后输出幅值为1的理想PWM控制波形控制Boost电路的占空比，从而控制输出电压的大小。

引入Step阶跃函数实现突变的辐照度和温度，仿真分别观察温度恒定（25℃）、辐照度突变时和辐照度恒定（1000W/m2）、温度突变时光伏组件的输出功率。温度恒定时，通过设定Step函数使组件的辐照度在 400（W/m2）、600（W/m2）、1000（W/m2）变化；辐照度恒定时，同样通过设置三个Step函数的参数使组件的温度在25℃、50℃、75℃变化。

3 仿真结果与讨论

辐照度和温度变化时光伏组件的输出功率分别如图3、图4所示。

图3、图4给出了不同工况下光伏组件的最大功率跟踪结果，在辐照度和温度分别变化时，组件输出功率能跟随相应的变化而变化。

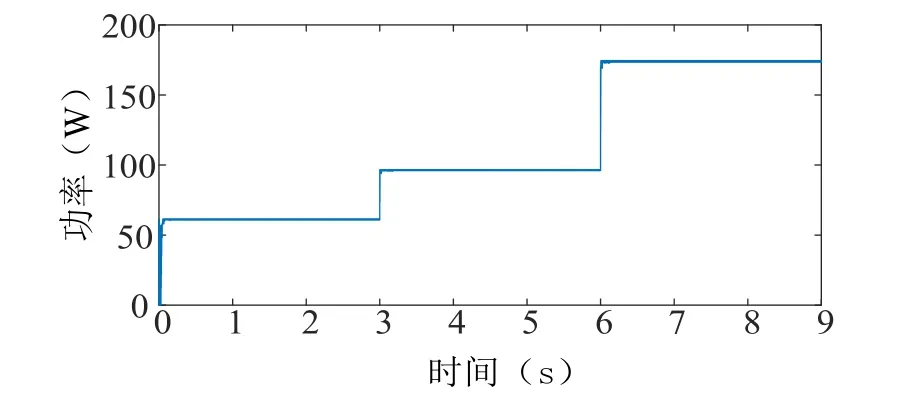
图3 温度恒定时组件输出功率

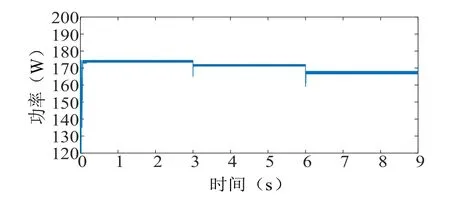
图4 辐照度恒定时组件输出功率

为进一步论证所建模型的跟踪精度，利用式（10）给出的辐照度和温度对光伏最大功率的影响规律，对不同工况下组件的最大输出功率的理论值进行计算，并将仿真结果与理论值进行比较，结果如表1所示。

需要澄清的一点是，本文采用简化光伏组件输出特性模型并不会对式（10）的理论计算结果产生影响。因此，将式（10）的理论计算结果作为比较的参考值是合理的，可行的。

表1 最大功率跟踪结果

由表1可知，在温度不变，辐照度变化时，光伏组件的输出特性曲线发生变化，所构建简化函数的最大功率跟踪模型能够使组件工作在最大功率点附近；同样，在辐照度不变，温度变化时，所给模型也能达到预期目的。并且，不同工况下最大功率跟踪模型的仿真结果与理论值的平均相对误差最大不超过1%，仿真结果的绝对误差不超过±2W，表明所建模型在辐照度和温度变化时均能准确地跟踪其最大功率。

进一步对表1进行分析可知，辐照度变化导致光伏组件最大输出功率点数值的变化幅度大于温度，产生上述现象的主要原因一方面是辐照度变化的幅值大于温度变化的幅值，另一方面是辐照度对输出特性曲线的影响效果也较温度显著。这一点与理论分析的结果一致，从另一个侧面证明了本文所给基于简化方程的最大功率跟踪仿真模型的有效性和准确性。