明确“初末位置” 构建“直线边界”——对称规律在有界磁场中的巧妙应用

李 进

(山东省邹平市第一中学,山东 邹平 256200)

1 问题的提出

2018年全国卷高考物理试题迎来了“带电粒子在磁场中运动”的全面回归,全国Ⅰ卷和全国Ⅱ卷均在第25题进行重点考查,总分20分,全国Ⅲ卷将其放在第24题,总分12分．该问题情境题目多、题型多、综合性强、难度大,能考查学生的分析综合能力和应用数学知识处理物理问题的能力．笔者在多年高三物理教学工作中发现,许多物理参考资料都是按照有界磁场的形状对题目进行所谓的归类,如“圆形磁场”、“三角形磁场”、“平行边界磁场”等．仔细分析就能发现,这些名词对解题并没有什么实际意义．

笔者发现,在粒子入射点和出射点确定的情况下可以进行如下处理:先连结入射点和出射点构建“直线边界”,然后利用粒子进出直线边界时运动轨迹的对称性分析问题．

2 带电粒子进出直线边界磁场时轨迹的对称性

从直线边界射入匀强磁场的粒子,从同一直线边界射出时,入射时速度与边界的夹角同出射时速度与边界的夹角相等,且等于圆心角的一半．

(1) 粒子速度与边界成直角时,粒子在磁场中运动半个圆周后垂直于边界射出磁场[如图1(a)所示].

(2) 粒子速度与边界成钝角时,粒子在磁场中运动一段优弧后射出磁场[如图1(b)所示].

(3) 粒子速度与边界成锐角时,粒子在磁场中运动一段劣弧后射出磁场[如图1(c)所示]．

以上是所有参考资料里面都有的内容,其弊端是会让学生认为只有题目中出现如图1所示的直线边界才能用以上结论处理问题,其实并非如此,以下将举例说明．

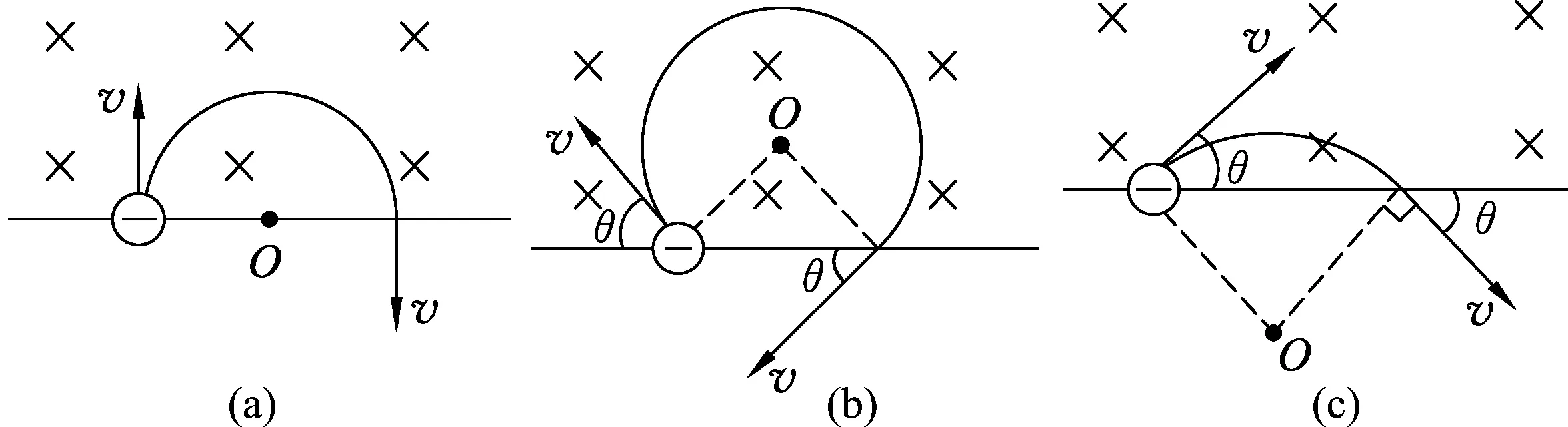
图1

3 举例

在各种形状的有界磁场中,只要粒子的初末位置确定时,连结初末位置则可以构建出“直线边界”,进而运用以上规律巧妙地分析问题．

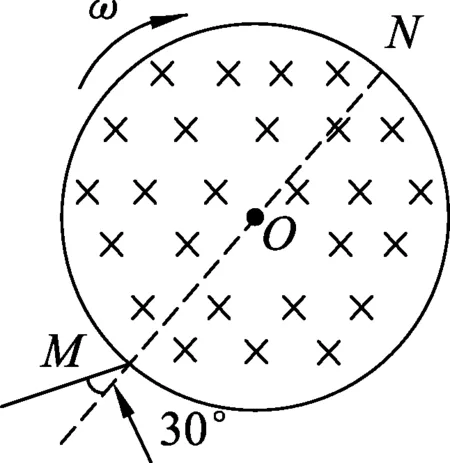
图2

例1.(2016年全国卷Ⅱ第18题)一圆筒处于磁感应强度大小为B的匀强磁场中,磁场方向与筒的轴平行,筒的横截面如图2所示．图中直径MN的两端分别开有小孔．筒绕其中心轴以角速度ω顺时针转动．在该截面内,一带电粒子从小孔M射入筒内,射入时的运动方向与MN成30°角.当筒转过90°时,该粒子恰好从小孔N飞出圆筒.不计重力.若粒子在筒内未与筒壁发生碰撞,则带电粒子的比荷为

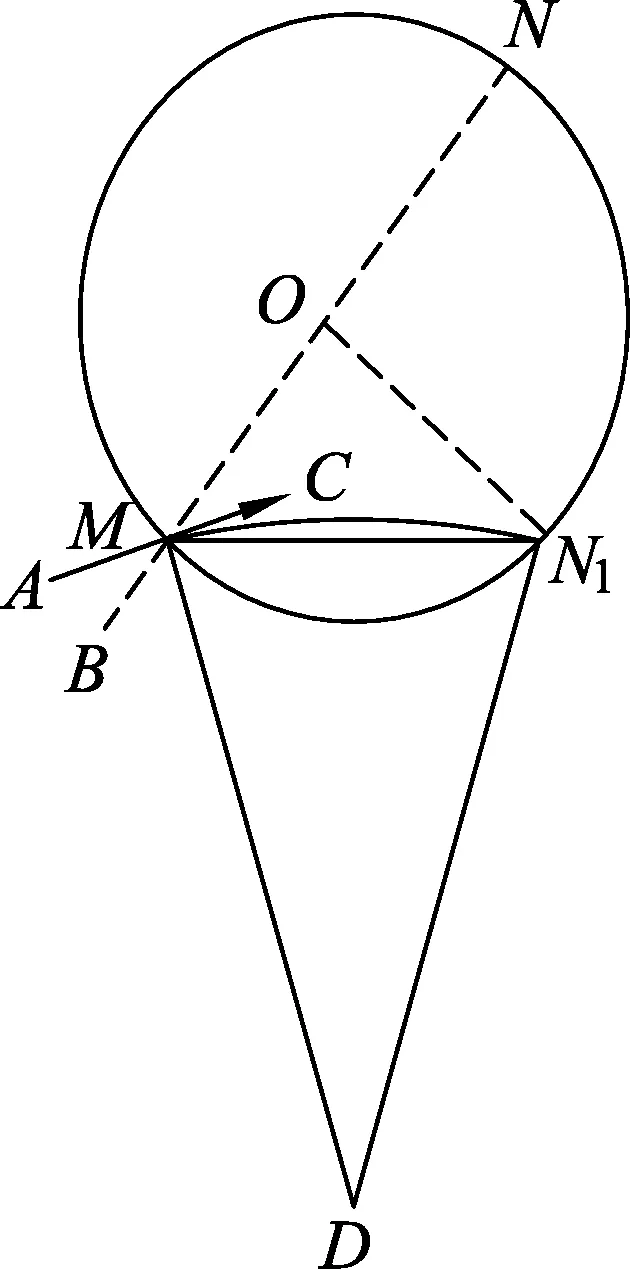
图3

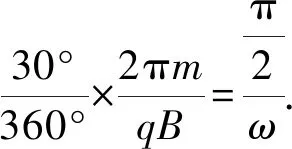
以上方法的优点在于,连接M与N1后,将该连线看做直线边界,根据圆心角等于弦切角的2倍这一几何关系迅速得出运动轨迹的圆心角的大小．

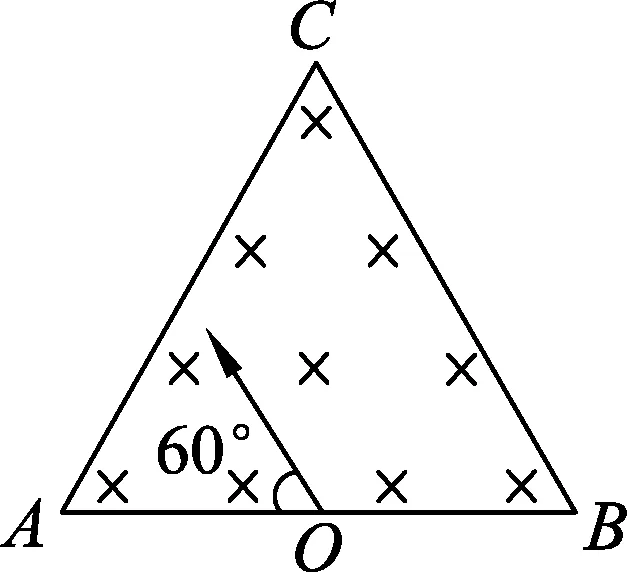
图4

例2.如图4所示,在边长为2a的正三角形区域内存在方向垂直于纸面向里的匀强磁场,一个质量为m、电荷量为-q(q>0)的带电粒子(重力不计)从AB边的中心O以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与AB边的夹角为60°,若要使粒子能从AC边穿出磁场,则匀强磁场磁感应强度的大小B需满足

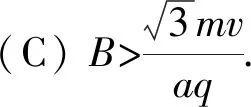
解析:解答该题的关键是判断带电粒子能否经过C点,若不能经过C点,则要判断何时轨迹与AC边相切．许多学生正是因为无法得出以上结论而不能正确解答该题．

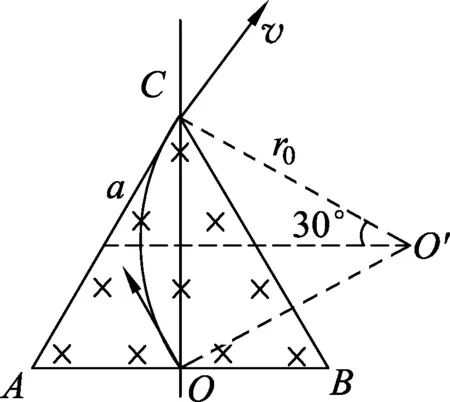
图5

其实,我们可以做如下处理:如图5所示,假设粒子能够经过C点,连结OC并延长,将其做为直线边界,则入射速度与边界夹角为30°,根据带电粒子进出直线边界磁场时轨迹的对称性可知,从C点出射时速度与边界夹角也是30°,从而得出经过C点时速度沿AC方向,且圆弧所对应的圆心角为60°．

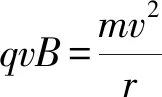
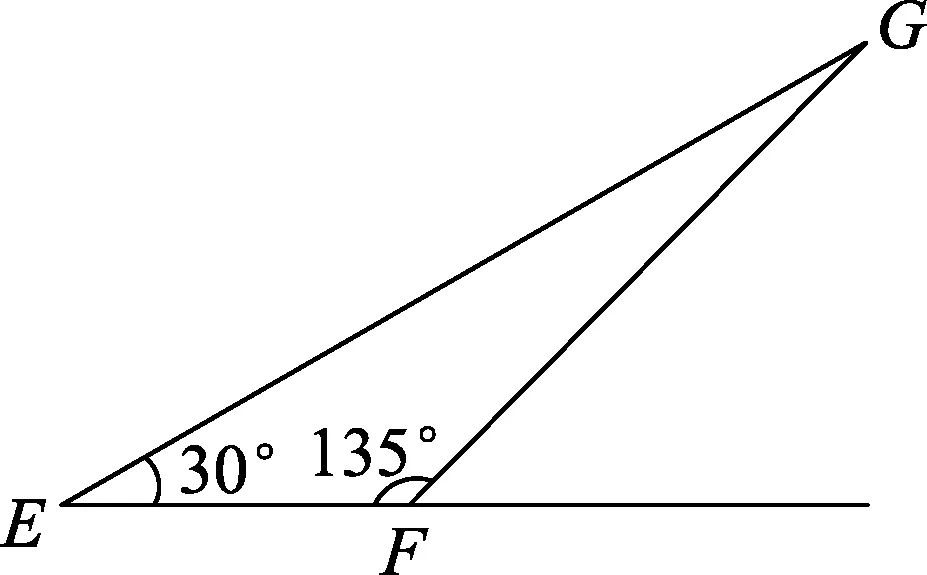
图6

例3.如图6所示,纸面内有E、F、G3点,∠GEF=30°,∠EFG=135°,空间有一匀强磁场,磁感应强度大小为B,方向垂直于纸面向外．先使带有电荷量为+q的点电荷a在纸面内垂直于EF从F点射出,其轨迹经过G点;再使带有同样电荷量的点电荷b在纸面内与EF成一定角度从E点射出,其轨迹也经过G点,两点电荷从射出到经过G点所用的时间相同,且经过G点时的速度方向也相同．已知点电荷a的质量为m,轨道半径为R,不计重力,求:

(1) 点电荷a从射出到经过G点所用的时间;

(2) 点电荷b的速度的大小．

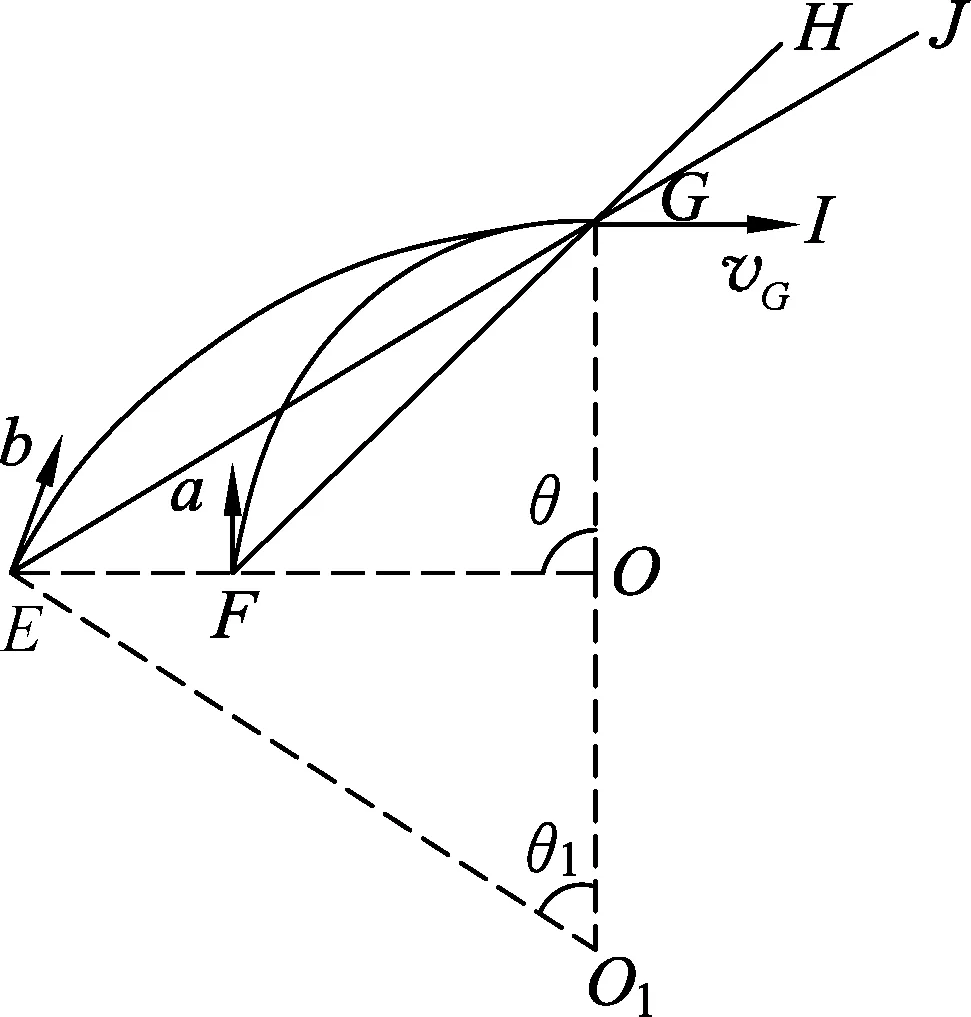
图7

解析:如图7所示,该题中a、b两个粒子分别从F点和E点出发并均经过G点,则分别连接FG和EG并延长,将它们看做直线边界．a粒子入射时速度与边界夹角为45°,根据带电粒子进出直线边界磁场时轨迹的对称性可知,a粒子到达G点时速度与边界夹角∠HGI也是45°(如图5所示)进而得出G点速度方向水平向右．a粒子轨迹的圆心角θ=90°．b粒子到达G点时速度方向与a粒子相同,也是水平向右的,该速度与EG连线的夹角为30°,再次根据带电粒子进出直线边界磁场时轨迹的对称性可知,b粒子从E点入射时速度方向与EG连线的夹角也是30°,它的运动轨迹所对应的圆心角θ1=60°．

(1) 设点电荷a的速度大小为v,由牛顿第二定律得

(1)

由(1)式得

(2)

设点电荷a做圆周运动的周期为T,有

(3)

如图7,O和O1分别是a和b的圆轨道的圆心．设a在磁场中偏转的角度为θ,b在磁场中偏转的角度为θ1,由几何关系得

θ=90°,θ1=60°.

(4)

故a从开始运动到经过G点所用的时间t为

(5)

(2) 设点电荷b的速度大小为v1,轨道半径为R1,依题意有

(6)

由(6)式得

(7)

由于两轨道在G点相切,所以过G点的半径OG和O1G在同一直线上．由几何关系和题给条件得

θ1=60°，R1=2R.

(8)

联立(2),(4),(7),(8)式,解得

(9)

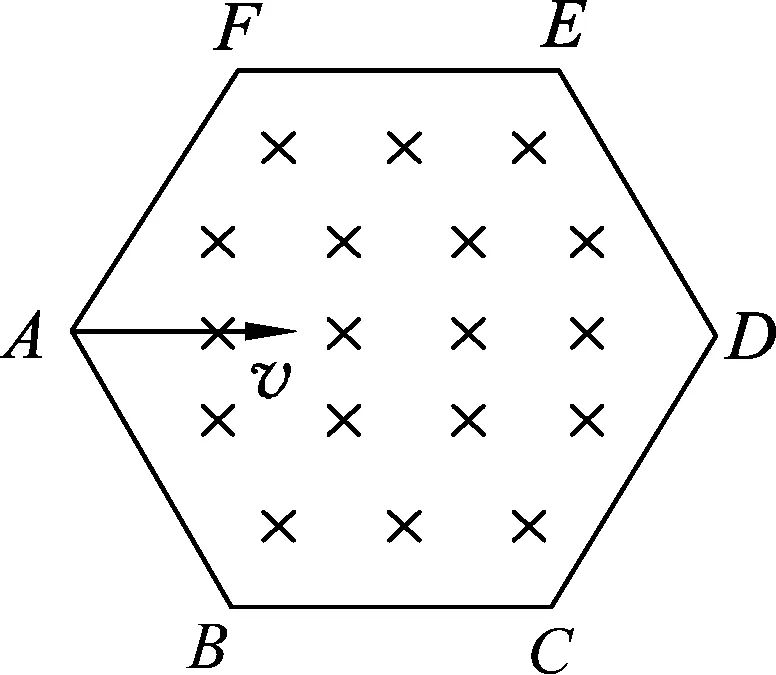
图8

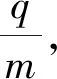
(1) 编号为①的粒子进入磁场区域的初速度大小;

(2) 编号为②的粒子在磁场区域内运动的时间;

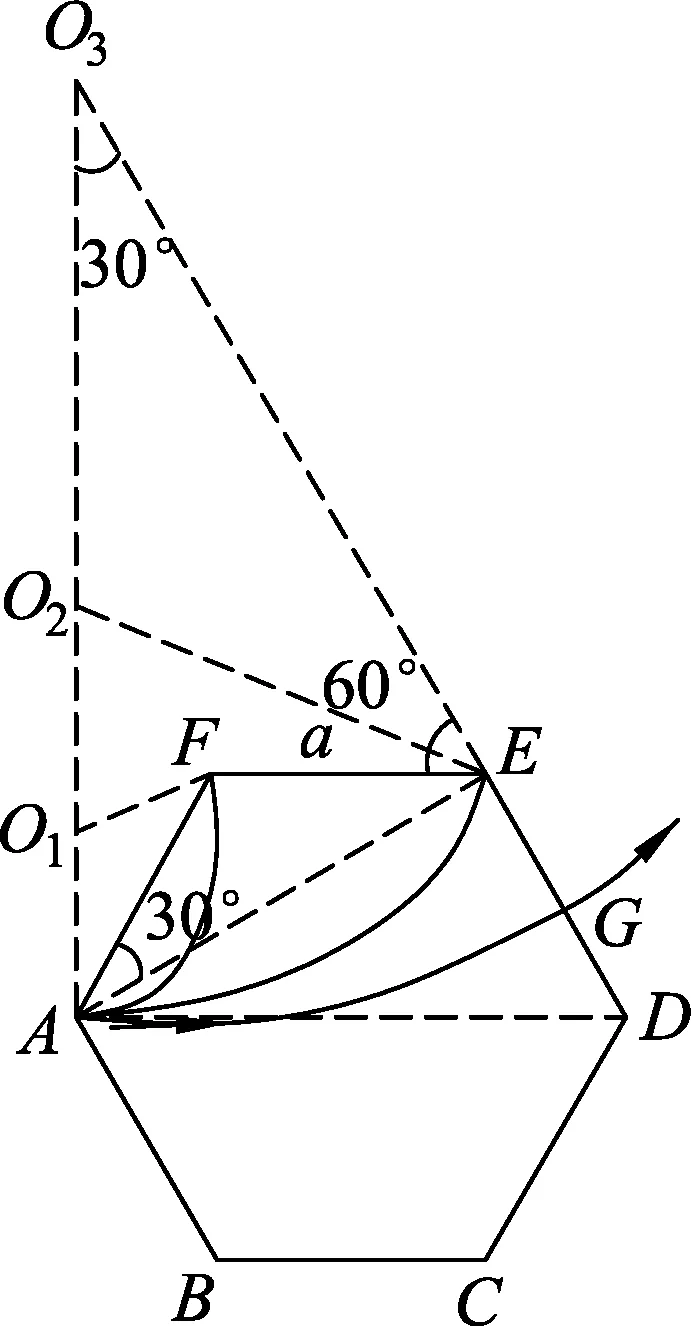
图9

(3) 编号为③的粒子在ED边上飞出的位置与E点的距离．

解析: (1) 如图9所示,设编号为①的粒子在正六边形区域磁场中做圆周运动的半径为r1,将AF看做直线边界,初速度大小为v1,与AF夹角为60°,根据带电粒子进出直线边界磁场时轨迹的对称性可知,轨迹所对应圆心角为120°．

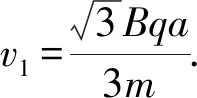
(2) 设编号为②的粒子在正六边形区域磁场中做圆周运动的半径为r2,线速度大小为v2,周期为T2,则

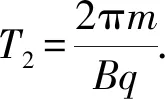
将AE连线做为直线边界,初速度与其夹角为30°,根据带电粒子进出直线边界磁场时轨迹的对称性可知,运动轨迹所对应的圆心角为60°,则粒子在磁场中运动的时间

(3) 设编号为③的粒子在正六边形区域磁场中做圆周运动的半径为r3,由几何关系可得

4 结束语

“带电粒子在磁场中的运动”是高中物理的重点,其难点主要在于“几何关系”的确定,包括圆心、角度、长度等．多数参考资料的试题讲解部分对“几何关系”的说明一带而过,不能帮助学生突破难点．通过以上分析可以看到,“直线边界”的构建可以帮助学生迅速拨开形状各异的有界磁场带来的“迷雾”,快速找到边角关系,进而顺利解决问题．