基于Craig-Bampton方法的海上风电机组基础结构超单元计算精度研究
2019-05-28王文华
钟 耀,王文华,周 润,李 昕
(1.中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014;2.大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024)
1 国内外研究进展综述
与陆上风能资源开发不同,海上风电场建设面临着复杂的环境条件,比如我国东部沿海地区的台风、环渤海海域的地震及海冰等均给海上风电机组(海上风机)及基础设计带来了技术挑战。上述复杂环境条件下如何建立海上数值仿真计算模型,并准确得到其结构响应已成为现阶段海上风电结构领域的研究重点。
目前,海上风电结构分析模型普遍采用整体耦合模型和半整体模型,整体耦合模型即直接建立包含转子—机舱—控制—塔筒—基础结构的整体结构数值仿真模型,并开展耦合时域反应分析,已广泛应用于浮式和固定式海上风机耦合机理及运行控制策略研究。Ma[1]、Li[2]、万德成[3]和刘颖莲[4]等均基于整体耦合模型揭示了Spar、TLP等不同类型浮式风机整体结构耦合反应机理。王洪哲等[5]采用整体耦合分析方法研究了极端风浪作用下海上风电结构响应规律,并提出了相应的运行控制策略。方通通[6]、Rezaei[7]和Koukoura[8]等采用整体方法开展了随机风浪作用下海上风电疲劳分析,系统研究了环境荷载耦合效应、风浪联合分布及控制策略等对于海上风电结构疲劳累积的影响。
由上述研究可得,基于整体耦合模型能够得到更为合理的海上风电结构反应,尤其对于结构疲劳累积;不过,方通通[6]和Kvittem[9]等指出采用整体耦合疲劳计算模型将显著增加数值仿真计算成本。与整体耦合模型不同,半整体模型通过基础结构等效刚度、质量矩阵代替相应有限元模型,建立转子—机舱—塔筒—等效特征矩阵的气弹数值仿真计算模型;将气弹分析所得风机荷载作用于塔筒与基础结构交接点,并施加其他环境荷载(如波浪、海冰、地震等)于基础结构有限元模型,计算得到海上风机结构响应。张戈[10]、夏露[11]、陈法波[12]和莫仁杰[13]等均采用该模型开展了风浪和地震等不同类型荷载作用下固定式海上风电结构动力反应计算,Minguez等[14]采用该方法系统对比了单桩、三桩和导管架基础结构的极限承载力。王鹏等[15]以基础结构用钢量为优化目标,采用半整体方法对海上风机三桩基础结构进行了优化设计。
本文对半整体模型关键技术基础结构超单元矩阵计算展开研究,探讨将Craig-Bampton方法应用于海上风机基础结构刚度、质量超单元矩阵计算时,其计算参数选取对于所得超单元矩阵计算精度的影响。进一步,分别建立固定式海上风电整体耦合模型和半整体模型,对基于Craig-Bampton方法所得超单元矩阵计算精度进行验证。
2 半整体模型运动方程
空气动力荷载作用下海上风电转子—机舱—塔筒—超单元的运动方程为
(1)

进一步,可得风机荷载作用下海上风机基础结构运动方程为
(2)

基础结构超单元计算普遍采用Craig-Bampton(C-B)方法[16]。Craig-Bampton方法将海上风机基础结构节点划分为边界节点和内部节点,划分后结构刚度和质量矩阵如下
(3)
基于该方法可得海上风机基础结构超单元计算公式,即
(4)
(5)
其中,
(6)
(7)
(8)
(9)
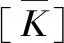
3 样本风机有限元模型
选用我国近海风电场软弱地基所应用的五桩基础结构,如图 1所示,并结合NREL 5MW基准风机[17]得到本次研究的样本海上风电机组,其中,NREL 5MW基准风机采用变速变桨式控制方式,轮子、轮毂直径分别为126、3 m,切入、额定、切出风速分别为3、11.4、25 m/s、切入、额定转速分别为6.9、12.1 rad/min。基于ANSYS[18],选用PIPE单元建立基础结构有限元模型。同时,选用COMBINE单元,基于p-y、t-z和Q-z承载力曲线建立非线性桩土相互作用模型。由此,所建立的基础结构有限元模型如图2所示。
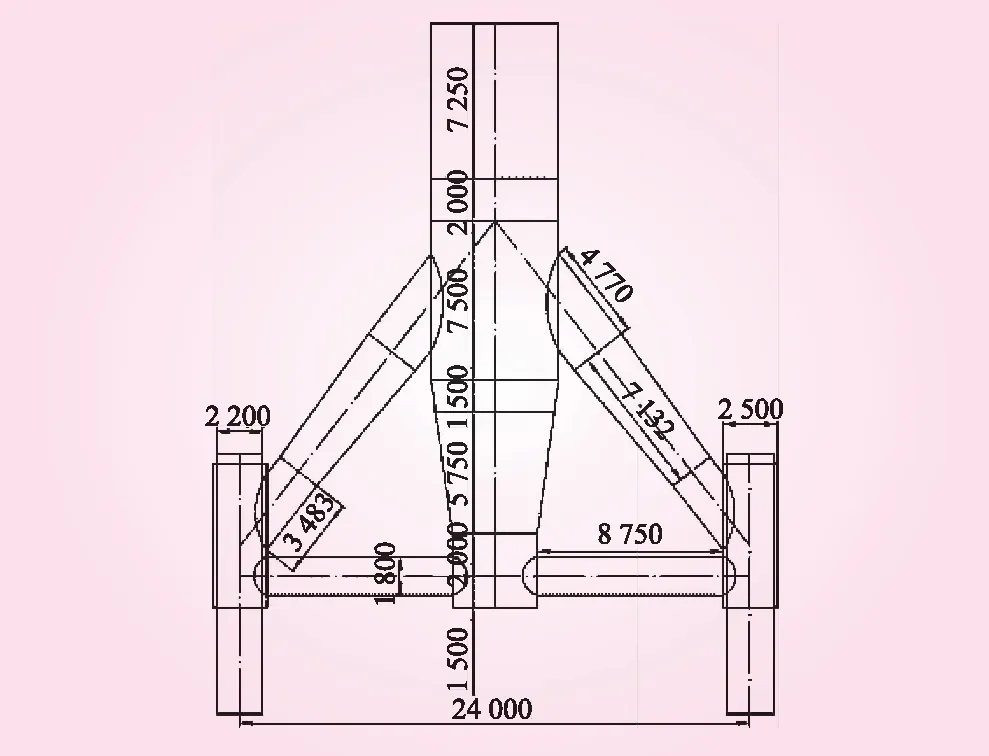
图1 五桩基础结构基本参数(单位:mm)

图2 五桩基础结构有限元模型
4 基础结构超单元计算分析
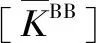
4.1 凝聚节点影响研究
基于图 2所示有限元模型主要杆件节点编号,分别选取基础结构主筒体模型节点1 000、2 000、3 000和4 000作为凝聚节点,开展图 3所示风机荷载Fx作用下,所选取凝聚节点对于C-B方法所得基础结构超单元计算精度影响研究。风机荷载Fx作用于基础结构顶部位置。
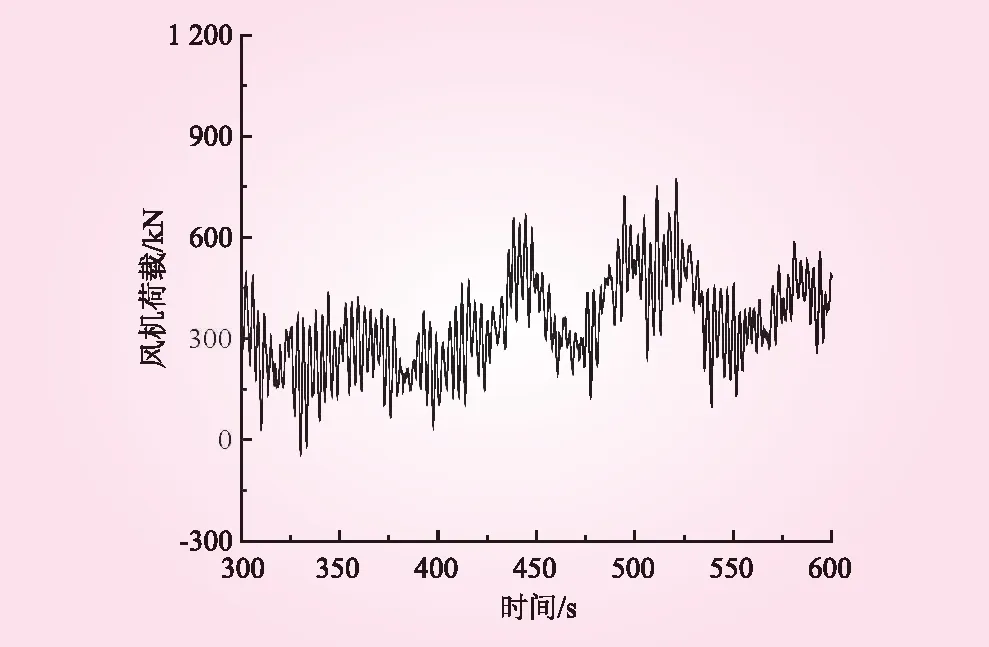
图3 风机荷载Fx
风机荷载作用下基础结构顶部位移统计值相对误差随所选取凝聚节点变化规律如图4所示,相对误差计算公式为
(10)
式中,S1为荷载作用下基于图2a所示有限元模型所得结构响应统计值;S2为考虑不同凝聚节点影响,基于基础结构超单元矩阵所得结构响应统计值。
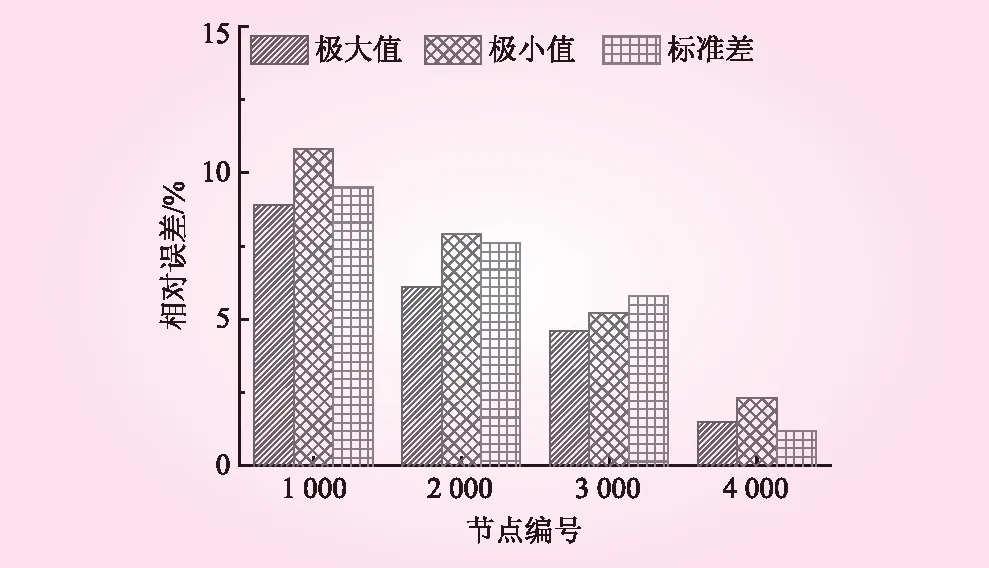
图4 基础顶部位移统计值相对误差
由图4可知,凝聚节点对于C-B方法所得基础结构超单元矩阵计算精度具有显著影响,相对于其他节点,当指定基础顶部节点(节点4 000)为凝聚节点时,所得超单元矩阵具有较高计算精度,此时所得基础结构顶部位移统计值最大相对误差仅为2.3%。
4.2 内部节点主模态数量影响研究
选取基础结构顶部节点4 000作为凝聚节点,同时分别选取基础结构内部节点前4、14、34、54、94阶模态作为主模态,基于C-B方法开展基础结构超单元计算。基于超单元计算结果,施加风机荷载Fx,所得基础结构顶部位移时程统计值与有限元模型计算结果时频域对比如图5所示。

图5 风机荷载作用下基础顶部位移时频域反应对比

(11)
(12)
由图5a可知,当所保留内部节点主模态数量为4阶时,此时C-B方法所得超单元矩阵具有较高的计算精度,如所得基础结构顶部位移统计值最大相对误差仅为2.5%。随着拟保留内部节点主模态数量的增加,超单元矩阵计算精度逐步提高。当所保留主模态数量达到34阶时,此时基于基础结构超单元矩阵所得风机荷载Fx作用下结构响应与有限元模型计算结果基本一致。
由图5b可知,对比包含不同阶数主模态向量的基础结构超单元矩阵,均能保证风机荷载Fx作用下基础结构位移反应控制频率与有限元模型计算结果保持一致,如所得结构反应主要控制频率均为0.319 Hz,故所选取超单元矩阵均具有较高计算精度。
因此,对于所选取风机荷载工况,当选用C-B方法开展基础结构超单元计算时,如若选取基础结构顶部节点为凝聚节点,同时内部节点主模态数量≥34阶,此时得到的超单元具有足够的计算精度。
5 基于整体耦合模型的海上风机超单元矩阵验证
依据样本风电结构参数,基于FAST[19]建立样本海上风电机组的整体耦合模型。同时,依据第4部分研究所得C-B方法计算参数选取原则,选取塔筒与基础结构交界点(节点4 000)为拟凝聚节点,将基础结构总刚度及质量矩阵凝聚至该节点,所得与该节点自由度相耦合超单元矩阵如式(11)和式(12)所示。
基于式(11)和式(12)所示超单元矩阵,依据半整体模型运动方程,建立样本的转子—机舱—塔筒—超单元矩阵半整体计算模型。
分别选取8、11.4 m/s和14 m/s平均风速,基于IEC Kaimal谱拟合得到随机风速1、2和3如图6所示,开展上述随机风速时程作用下海上风电整体耦合与半整体模型对比研究。随机风速1作用下,基于整体耦合模型和半整体模型所得样本海上风电机组塔筒顶部推力荷载、加速度时程响应统计值对比如图7所示。
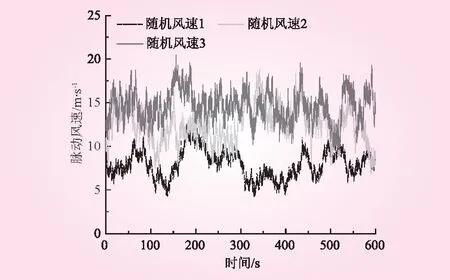
图6 随机风速时程
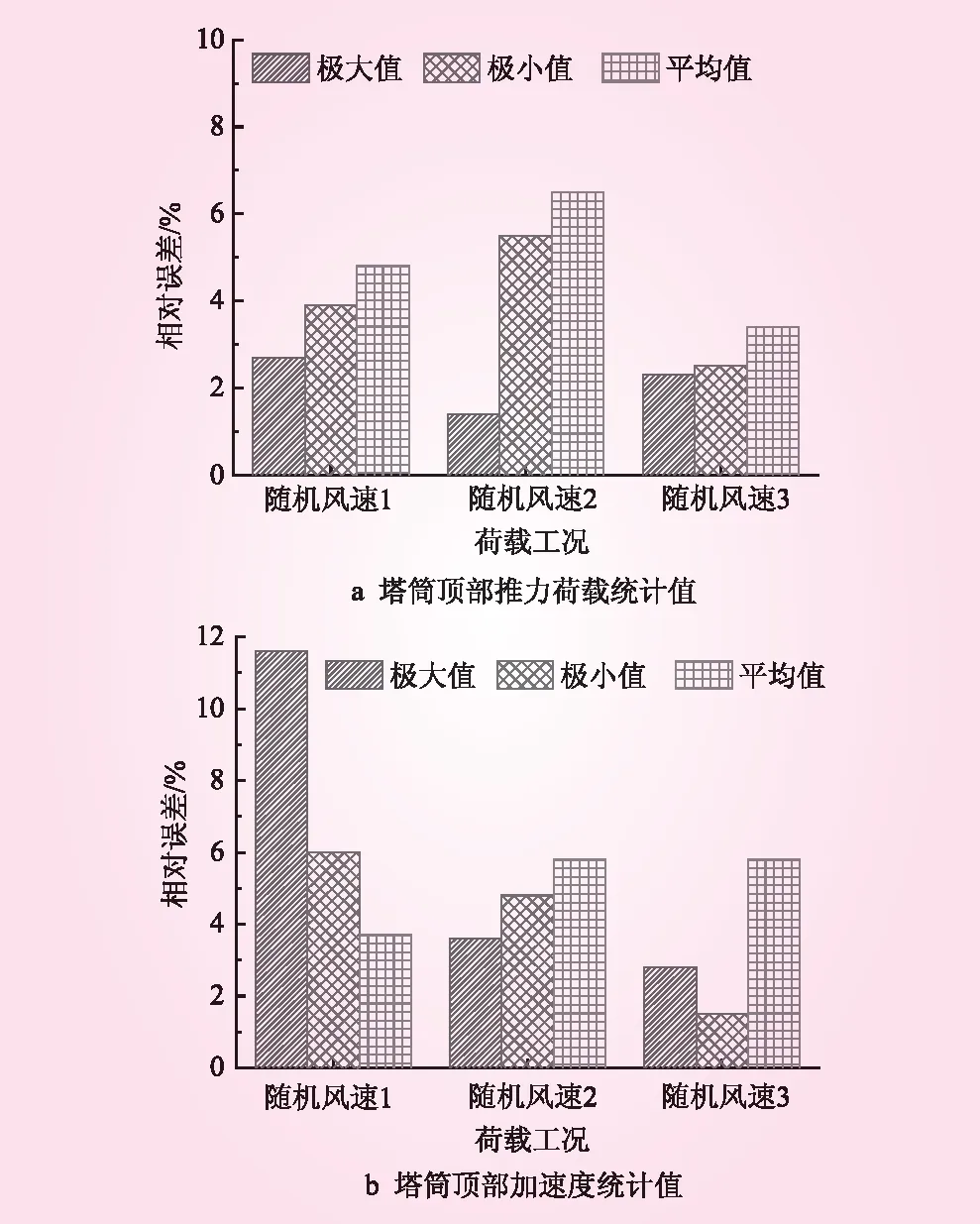
图7 随机风速作用下海上风电机组运动响应统计值计算误差
由图7可知,基于整体耦合模型和半整体模型所得海上风电结构运动响应基本相同。由图7a可知,对于塔筒顶部推力荷载,随机风速2作用下,基于上述模型所得结构响应平均值计算误差最为显著。随机风速2的平均风速为额定风速,即在该风速作用下风机将启动变桨控制策略。由此,进一步对比可得,由于变桨控制策略影响,随机风速3作用下推力时程均值相对误差相对于随机风速2作用工况明显减小。由图7b可知,与塔筒顶部推力荷载变化规律稍有不同,随机风速1作用下,半整体模型所得塔筒顶部加速度时程极大值和极小值相对误差最为明显,此时计算误差将分别达到11.6%和6.0%。需指出,在随机风速2和3作用下整体与半整体模型所得加速度时程统计值基本一致,比如上述工况下半整体模型所得加速度统计值最大相对误差仅为5.8%。
综上所述,将塔筒与基础结构连接节点指定为基础结构总刚度和质量矩阵凝聚节点,基于C-B方法所得超单元矩阵建立海上风电半整体计算模型所得结构时频域响应与整体耦合模型计算结果基本一致。此外,海上风机运行状态及控制策略对于半整体模型计算精度具有显著影响,在达到额定风速后,启动相应变桨控制策略将显著提高半整体模型塔筒顶部推力荷载计算精度。
6 结 论
本文通过与整体耦合模型的对比,验证了基于C-B方法计算得到基础结构超单元矩阵建立海上风电半整体模型的计算精度。通过本次研究可得以下结论:
(1)基于有限元模型研究可得,凝聚节点选取对于Craig-Bampton方法所得超单元矩阵计算精度具有显著影响;对于所选取工况,当凝聚节点选取为基础结构顶部节点时,所得超单元矩阵具有较高计算精度。
(2)内部结点主模态数量对于超单元矩阵计算精度的影响亦不可忽视;对于所列工况,当内部主模态数量达到34阶时,此时所得超单元矩阵计算结果与有限元模型基本一致。
(3)选取塔筒与基础结构交界点为凝聚节点,基于C-B方法所得基础结构超单元矩阵建立半整体模型所得海上风电结构运动响应与整体耦合模型计算结果基本一致。
(4)半整体模型计算精度与海上风机运行状态及控制策略密切相关,在额定风速以上启动变桨控制策略后,将显著提高半整体模型塔筒位置推力荷载计算精度。
