基于秩相关系数的区间数型水质量评价模型及其应用
2019-05-28张建配朱恒华
贾 超,袁 涵,杨 晟,张建配,陈 阳,朱恒华
(1.山东大学土建与水利学院,山东 济南 250061;2.山东大学海洋研究院,山东 青岛 266237;3.山东省地质调查院,山东 济南 250000)
区域阶段性水环境综合评价中,水质监测值与分级标准均为区间数[1],两者之间具有模糊的非线性关系。由于数据类型的限制,传统评价法中的综合指数评价法、灰色关联度法、Topsis法、模糊综合评价法等[2]难以对区间数型水质进行评价,使区间数型水质评价成为一个难点。一种常规做法是将该时期内的多个时间段监测的平均值代替区间数进行评价[1,3],但这种处理并非合理。因此,在不少学者将区间数型多属性决策理论引入到区间数型水质评价中,推动了区间数型水质评价理论的发展。文献[1,3-5]都不同程度地对区间数型水质的评价研究进行了探索突破,但或多或少都存在计算复杂或与其他方法不易结合等问题。
目前,对区间数型水质评价方法的研究尚未形成统一的认识,有必要进一步对区间数型水质的评价方法进行探讨分析。在多属性决策评价中,两个方案的贴近程度可以用属性相关测度的度量值来描述[6],当越多的属性相关测度相似,则两个方案就越贴近。Spearman秩相关系数是非参数统计理论中常用的评价系数,适用于同一研究中两个方案在相同属性(方案属性个数≥4)下的一致性评判[6-8],故当两个方案的Spearman秩相关系数越大,则可以判定,两个方案的接近程度越大。因此,借鉴目前关于Spearman秩相关系数在多属性决策问题[9]及区间数理论中的研究成果[6],尝试将Spearman秩相关系数和区间数型水质评价问题结合,通过将水环境质量标准与拟评价水质监测样本构建成区间数表示的方案集,并借鉴灰色关联法确定相对最佳方案。根据相关属性计算各方案与相对最佳方案的Spearman秩相关系数,由模式识别确定拟评价水质的等级,从而构建一种基于区间数型多属性决策理论及统计学原理[2-10]的区间数型水质评价的新模型。
1 区间数及其Spearman秩相关系数
定义1:随机样本X=(x1,…,xn)按随机变量取值大小进行排列的先后次序(x(1),x(2),…,x(N))称为随机样本X的秩次[9]。记另一样本Y=(y1,…,yn)的秩次为(y(1),y(2),…,y(N)),则样本X与样本Y的Spearman秩相关系数为
(1)
式中,di=x(i)-y(i)为秩次差;i=1,…,n,n为序列长度。
显然,Spearman秩相关系数满足:①rs(X,Y)=rs(Y,X);②rs(X,Y)|≤1;③若rs(X,Y)=1,则X与Y正相关;④若rs(X,Y)=-1,则X与Y负相关。
(2)
式中,当j=1,di=R(aL)-R(bL);当j=2,di=R(aR)-R(bR)。
显然,Spearman秩相关系数满足:①rs-ce(A,B)=rs-ce(A,B);②rs-ce(A,B)|≤1;③若rs-ce(A,B)=1,则A与B正相关;④若rs-ce(A,B)=-1,则A与B负相关。
2 区间数型水质评价模型的构建与步骤
2.1 构建区间数初始评价矩阵A
设待评价区有m个水质断面(监测站点),s个标准评价等级(水质量标准等级通常为5个等级),n个水质评价指标,则区间数初始评价矩阵A为
(3)
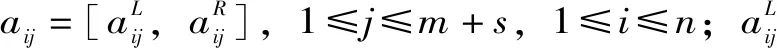
2.2 构建区间数标准决策化矩阵B
目前关于区间数型属性值规范化的研究较多,目前常用的区间数型属性值规范化方法有向量规范化法、比重变换法、极差变换法、指数函数法、误差传递法等[10],为便于对区间端点值为0的区间数属性值规范化,同时将效益型指标和成本型指标趋同化处理,通常采用极差变换法对区间数型指标进行处理。效益型区间数属性规范化,即
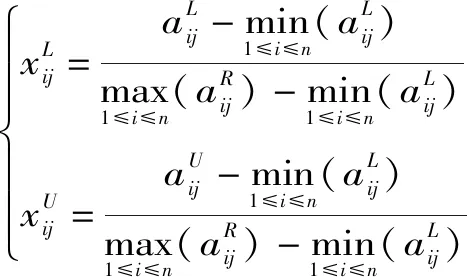
(4)
成本型区间数属性规范化为
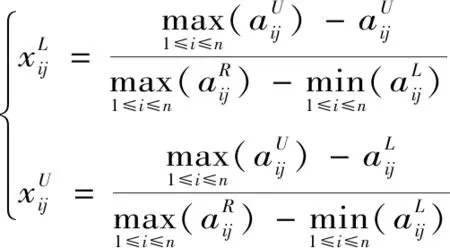
(5)
将初始评判矩阵A采用式(4)和式(5)进行规范化即可得到标准规范化矩阵
(6)
2.3 确定各指标属性权重W
水质监测具有时序性,对时长跨度不大的研究区域,水质指标的监测值在一定范围内保持稳定状态,可以根据水质监测数据进行各指标对水质等级评价贡献的量化。即,确定各指标的权重。常用指标权重的确定方法有主观评价法(如AHP)、客观评价法(如熵权法、超标指数法)、组合权重法以及变权理论等[11]。权重确定的方法选取在一定程度上代表了研究者对研究问题的认识和理解,相关方法在不同参考文献[4,12,15-16]中均有体现,本文不再赘述。
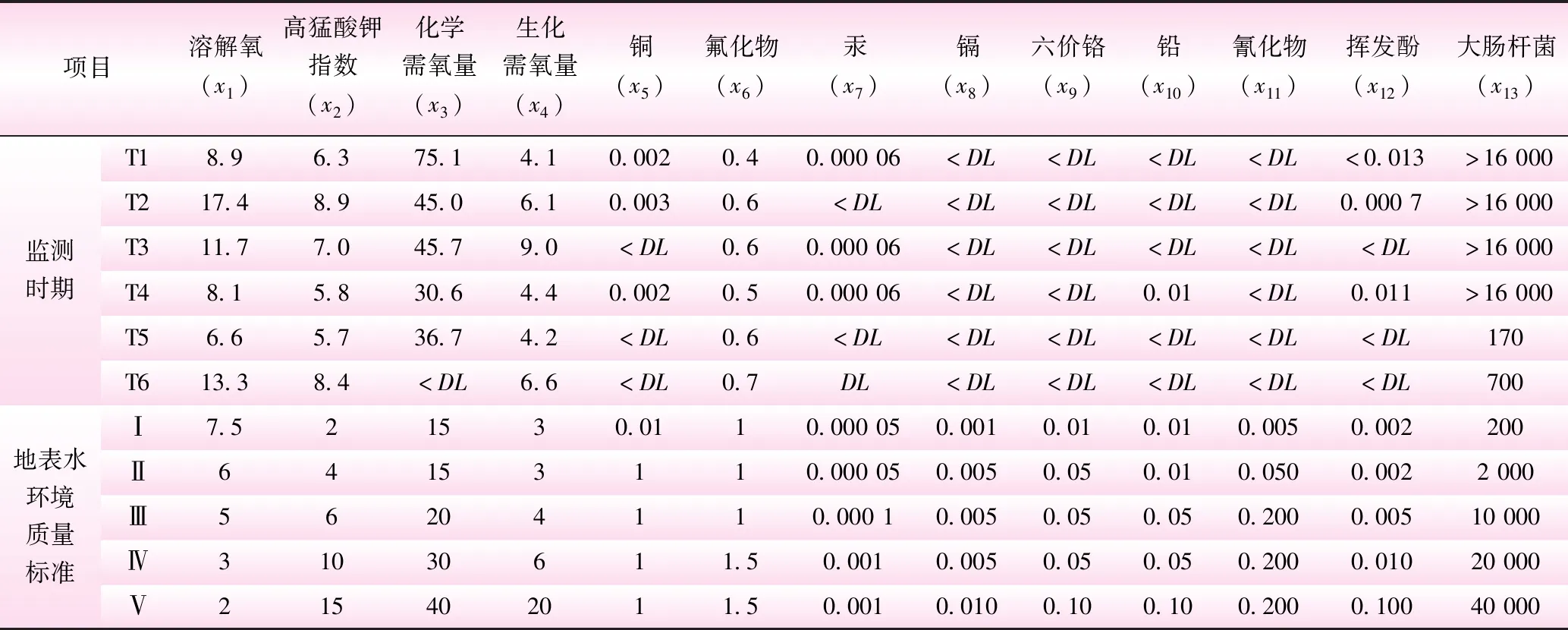
表1 监测断面部分水质监测结果及地表水环境质量标准
2.4 建立加权规范化矩阵C及确定相对最佳方案x*
根据各指标属性的权重向量W,建立加权规范化矩阵
(7)
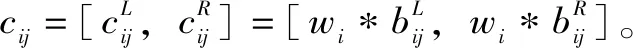
(8)

2.5 Spearman秩相关系数计算及方案排序评价
根据式(8)确定相对最佳方案,由式(4)计算加权规范化矩阵C中s个标准方案、m个水质断面与相对最佳方案的Spearman秩相关系数,得到s个标准方案、m个待评价水质断面的Spearman相关系数向量矩阵r=[rk1-ce,rk2-ce,…,rks-ce,…,rk,s+m-ce],根据各方案与相对理想方案的Spearman秩相关系数,进一步计算可得到m个待评价水质断面与s个标准方案的相对海明(hamming)距离
d(R,j)=|rkR-ce-rkj-ce|
(9)
则,最小相对海明距离对应的类别即为评价水体的水质质量级别。
3 实例应用
3.1 数据来源及区间数矩阵构建
研究数据来源于2006年浑河沈阳东陵大桥监测断面的部分实测水质数据[1],相关数据见表1。
由步骤2.1及表1中最小值和最大值构造区间数矩阵。
3.2 加权规范化区间数矩阵及其理想方案
根据表1的数据,耗氧量x1为效益型指标,由步骤2.2采用式(4)计算,其余指标采用式(4)可计算得到规范化评价矩阵,并采用权重向量[2]:
W=[0.209,0.133,0.174,0.143,0.005,0.094,0.035,0,0,0.27,0,0.064,0.118]
由步骤2.2~2.4可得到加权规范化矩阵:


由步骤2.4中式(8)及加权规范化矩阵可确定相对最佳方案为:
CL*=[0.063 9,0.115 3,0.139 3,0.121 5,0.005,0.050 1,0.033 3,0,0,0.026 7,0,0.062 7,0.117 4]
CR*=[0.209,0.133,0.174,0.143,0.005,0.094,0.035,0,0,0.027,0,0.064,0.118]。
3.3 Spearman秩相关系数计算与方案排序评价
根据式(2),得到各方案的Spearman相关系r,以等级Ⅰ的区间数型水质数据为例计算等级Ⅰ与理想方案的Spearman相关系数(见表2)。
由式(2)可以计算得到rⅠL-ce=0.994 5;同理,求得rⅠR-ce=1,则rⅠ-ce=0.997 3。参照等级Ⅰ与相对最佳方案的Spearman相关系数计算,得到各方案与相对最佳方案的左、右Spearman相关系数(见表3)。
由表3得到各方案与相对最佳方案的Spearman秩相关系数矩阵则,待评价监测段与地下水标准等级之间的秩相关系数海明(hamming)距离为:d(Ⅰ,监测段)=0.148 4;d(Ⅱ,监测段)=0.107 2;d(Ⅲ,监测段)=0.090 7;d(Ⅳ,监测段)=0.055;d(Ⅴ,监测段)=0.240 8;由计算结果排序判定浑河沈阳东陵大桥断面水质为Ⅳ类。
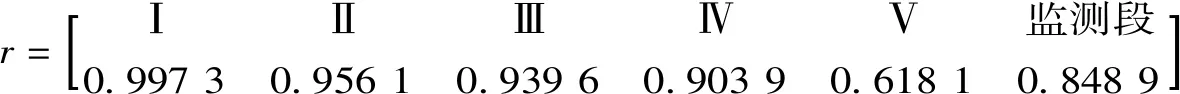
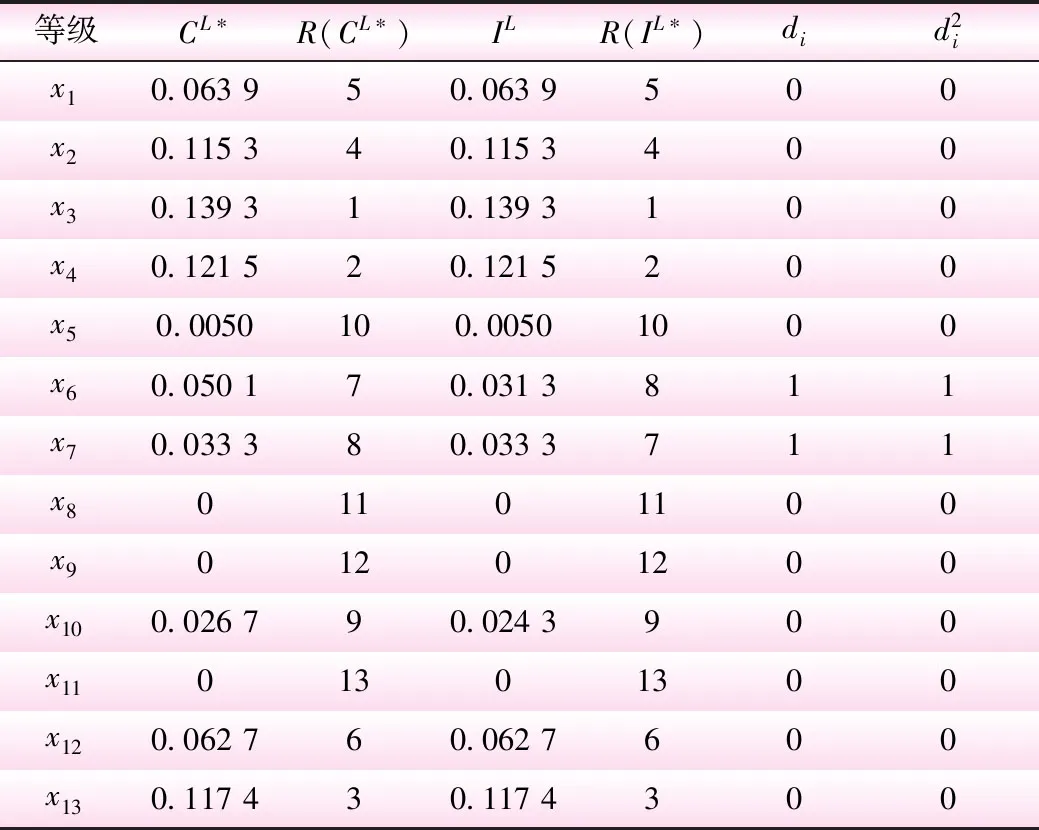
表2 等级Ⅰ和A*左区间的Spearman秩相关系数

表3 方案集与相对最佳方案的Spearman秩相关系数
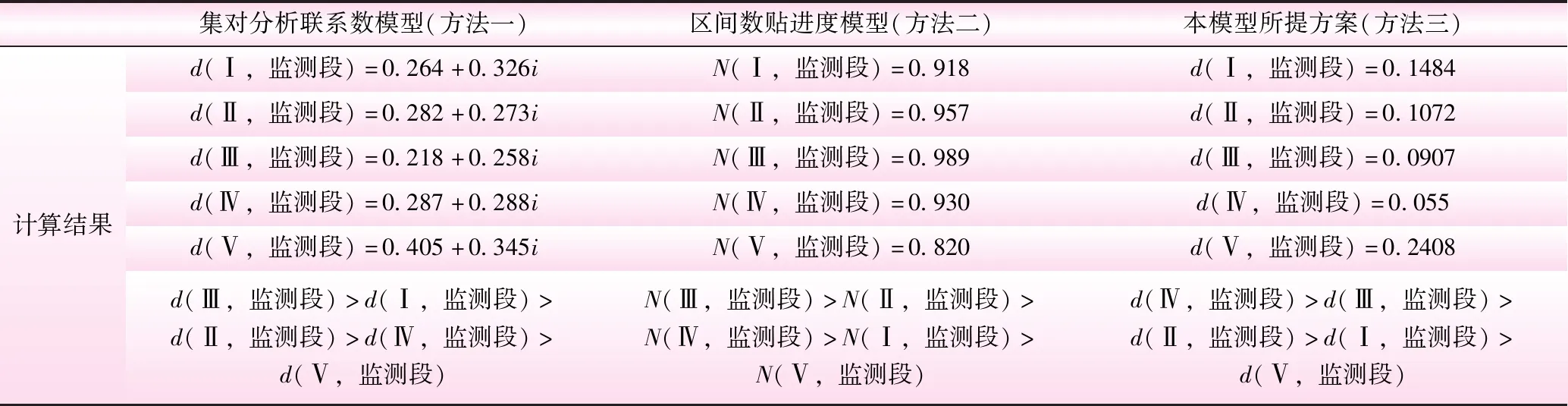
表4 不同方法下本案例的计算结果对比
3.4 结果评价分析
基于集对分析联系数的模型[2](方法1)、基于区间数贴进度的模型[13](方法2)与本文构建的模型(方法3)在本实例上的计算结果对比见表4。
由表4可知,3种评价方法评价结果相近,其中本模型(方法三)的评价级别为Ⅳ类水,要比方法一、方法二得到的评价结果高1个级别,本模型的水质评价结果更偏劣类水;从排序结果上分析,方法三和方法二排序一致性较高,评价结果均偏好Ⅱ~Ⅳ类,水质类别更偏离最劣(Ⅴ类水)和最优(Ⅰ类水),而方法一评价结果偏好Ⅰ~Ⅲ类。同时由图1分析,6个监测期13个监测因子中近50%的监测因子实测浓度处于Ⅰ类水,Ⅱ类水和Ⅲ类所占比例较少;监测期T1~T4内,13个监测因子中近40%的监测因子实测浓度处于Ⅳ类水和Ⅴ类水界限范围内;监测期T5~T6内,近20%的监测因子实测浓度处于Ⅳ类水和Ⅴ类水界限范围内。根据实测数据统结果显示,6个时期内高锰酸钾指数、化学需氧量、生化需氧量、挥发酚及大肠杆菌等指标监测值均在Ⅳ~Ⅴ类,所占权重分别0.133、0.174、0.143、0.064、0.118,权重占比较大。对比水环境质量标准,方法二和方法三的排序结果更为准确。将实测水质数据和标准进行对比分析,监测断面在6个监测时期内的高锰酸钾指数、化学需氧量、生化需氧量、挥发酚及大肠杆菌等指标监测值均在Ⅳ~Ⅴ类,其余指标监测值多在Ⅰ~Ⅱ类;方法三的水质评价为Ⅳ类较为合理。
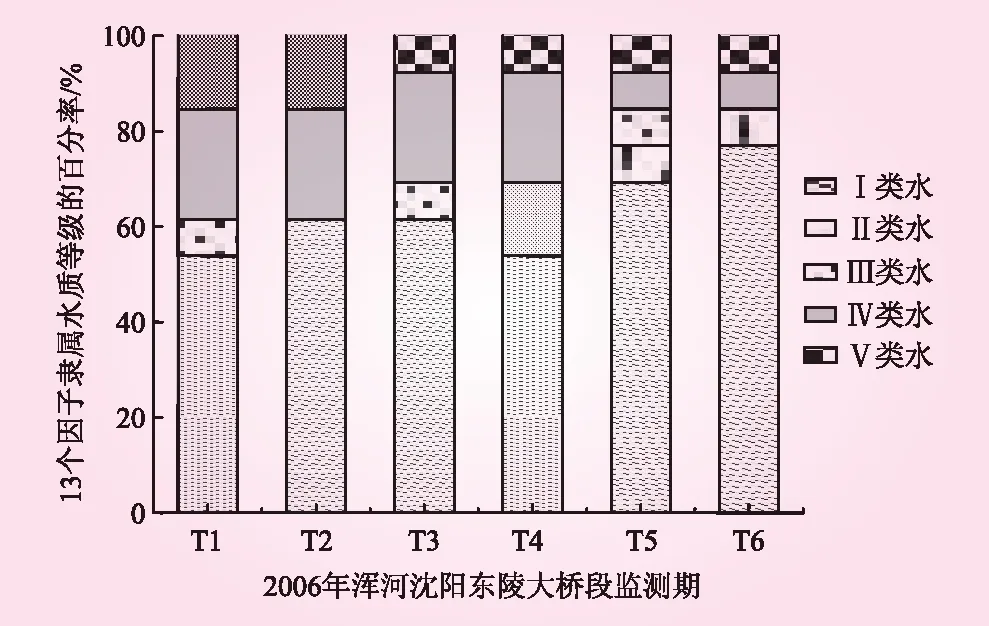
图1 13个指标监测值隶属各类水的个数百分率比较
方法三与其他评价方法得到的评价结果存在差异的主要原因:一方面是该模型在数据处理中为使效益型指标和成本型指标趋同化,采用了极差规范化处理;另一方面是模型采用的评价原理不同,但评价结果均是客观有效的。
4 结 论
(1)阶段性区域水环境评价中,以区间数表示多时段的水质监测结果,一方面可以有效避免了因采用平均值替代导致的水质数据利用不足;另一方面,可以对多时段水质监测结果的水质评价进行简化。
(2)Spearman秩相关系数具有明确的统计学意义,可以比较同一研究对象的不同方案的接近程度,将其应用于多属性方案决策中可以使问题简化,具有计算意义明确,计算过程简单等优点。
(3)将统计学思想融入到区间数型水质量综合评价中,根据构建的方案集与相对最佳方案的Spearman秩相关系数大小进行方案优劣排序,进而避开了区间数无法直接进行比较的难点,简化了区间数型水质的评价过程,在某种意义上扩充了区间数型水质评价的处理。实例验证,并与区间数集对分析法和区间数贴近度法比较表明,该模型处理区间型水质评价问题是客观有效的。
