基于EMD-FOA-BP神经网络的大坝变形预测研究

黄军胜，黄良珂，刘立龙，谢劭峰

(1.广西壮族自治区水利电力勘测设计研究院，广西南宁530023；2.桂林理工大学测绘地理信息学院，广西桂林541004；3.广西空间信息与测绘重点实验室，广西桂林541004)

大坝变形受水压、时效及气温等综合因素影响[1]，具有随机性与非线性的特点，建立大坝变形与影响因子关系的精确模型较为困难。传统时间序列法和回归分析法的非线性能力不足，且依赖于初始参数，无法满足大坝变形预测的高精度要求。针对变形数据非线性特点，文献[2]利用小波去噪方法对大坝变形数据进行分解，通过多尺度预测分析，有效提高了模型的泛化能力和非线性序列的预测精度。但小波分解不具备自适应的特点，小波函数与分解尺度通过经验确定，难以实现最优分解。Huang等[3]于1998年提出了一种新的信号处理方法——经验模态分解(EMD，empirical mode decomposition)，该方法将非线性、非平稳信号自适应地分解为有限个相对平稳的分量，即可对数据进行平稳化处理。文献[4-5]将EMD应用于变形监测、预测中，并通过与小波分解对比，可知EMD的数据处理过程更为简单直观，分解的层数由时间序列特征自适应确定，具备更好的自适应能力，为模型预测提供了较好的平稳环境。近年来，BP神经网络在非平稳时间序列建模的应用中发展很快，其具有良好的非线性映射能力、自适应能力和学习能力[1，6]。但BP神经网络模型对大坝变形非平稳序列的映射能力不足，且收敛速度慢以及易陷入极值等缺点使预测精度不理想。潘文超等提出一种全局寻优能力强、收敛速度快的果蝇优化算法(FOA，Fruit Fly Optimization Algorithm)，算法原理简单，受参数限制小，且具有鲁棒性和辨识精度高等特点[7]，能够优化神经网络内部结构，有效克服网络自身缺陷[8，9]。文献[10]利用FOA优化神经网络，弥补了神经网络先天不足，较快较准地找到网络中最佳平滑因子，与文献[6，11]利用思维进化算法(MEA)和粒子群算法(PSO)优化神经网络一样，虽然都提高了变形预报精度，但在网络训练过程中，较难捕捉学习到外部环境非线性变形量的规律，致使仿真精度欠佳。基于上述研究，本文将利用EMD对BP网络进行外部环境平稳化处理；再利用FOA对BP网络进行内部优化，即利用FOA的全局寻优能力强、搜索效率高等特点，为BP网络提供最优初始权值和阈值，克服网络自身缺陷，从而建立EMD-FOA-BP模型，应用于大坝变形预测。

1 经验模态分解原理

经验模态分解(EMD)作为一种常用的信号处理方法，能自适应地将非线性、非平稳时间序列的不同特征逐级分解，得到不同频率的本征模函数(IMF)和一个趋势项(B)。分解得到的每个IMF必须同时满足2个条件[12]：①在待分解信号中，极值点的数目与过零点的数目相等，或最多相差1个；②在任一时刻，上包络线(局部极大值的包络)与下包络线(局部极小值的包络)的平均值为0。其分解过程如下[13]：

(1)利用三次样条插值函数，将识别出的原始信号Y(t)所有极值点拟合出上包络线Vmax(t)和下包络线Vmin(t)。

(2)计算包络线的平均值ω1(t)，ω1(t)=Vmax(t)+Vmin(t)/2。

(3)令原始信号Y(t)与包络线平均值ω1(t)做差，可得D(t)，D(t)=Y(t)-ω1(t)。

(4)依据IMF的2个条件，得到第1个分量。若D(t)满足条件，则作为第1个IMF，记为L1；若不满足条件，则把D(t)视为新原始信号，重复步骤(1)～(3)，直到满足IMF条件为止。

(5)将(4)中所得分量L1从原始信号Y(t)中分离，得到残差信号B1，B1=Y(t)-L1。

(6)再把B1作为新的原始数据，重复步骤(1)～(5)，分解得到若干个IMF，直到Bn成为一个单调函数或者残余量函数值小于给定的阈值时，停止分解。此时，原始信号Y(t)表示为Y(t)=∑ni=1Li+Bn。

2 果蝇算法优化BP神经网络

果蝇优化算法意在帮助优化主体寻找最优解，其原理仿效于果蝇，利用灵敏的嗅觉器官感知空气中某种味道，再利用敏锐的视觉器官到达目标位置。

FOA优化BP网络的基本思路[9]是以果蝇个体的位置代表BP网络中的权值和阈值，初次仿真所得误差的平方和作为适应度函数，再给定每只果蝇随机方向与距离，计算一次迭代中最佳味道浓度的果蝇位置，通过迭代寻优，得到全局最佳味道浓度的果蝇位置，即BP神经网络的最优权值、阈值，其表达式过程如下[14]：

(1)初始化果蝇位置，即(Xi，Yi)=(X0，Y0)。

(2)给定每只果蝇能够搜索到最优位置的随机方向(XF，YF)和距离m，即(Xi，Yi)=(XF+m，YF+m)。

(3)计算预估最佳位置到原点的距离Di，Di=X2i+Y2i，并计算距离Di的倒数，即味道浓度判定值Si，Si=1/Di。

(4)将上式中味道浓度判定值Si带入适应度函数F(味道浓度判定函数)，得到该果蝇个体所处位置的味道浓度值Ti，Ti=F(Si)。

(5)搜索果蝇群中浓度最佳的果蝇Gbest(Ti取最小值[14])，即Gbest=min(Ti)。

(6)果蝇群利用视觉飞向目标，求解最佳味道浓度的果蝇位置(Xbest，Ybest)，即求解本次迭代最优权值、阈值。

(7)重复执行步骤(2)～(5)，迭代寻找最佳味道浓度，判断当前迭代的最佳浓度是否优于前一次的最佳浓度，若是则执行步骤(6)，更新最优权值、阈值。

(8)将最优权值、阈值引入BP神经网络中，进行网络训练，实现优化目的。

3 EMD-FOA-BP神经网络预测模型

3.1 模型预测流程

以不同观测时间段的大坝变形值组成一个时间序列{X(t)，t=1，2，…，m}，使用上述EMD对其进行分解得到n个本征模函数IMFi(i=1，2，…，n)和1个余量B。以前w期的大坝变形值为训练样本，将各IMF和余量B序列，分别建立经果蝇算法优化的BP神经网络模型(FOA-BP)，然后对后(m-w)期进行仿真。设各分量的预测值为YIMF1，YIMF2， …，YIMFn，和YB，模型预测流程见图1，则最终的EMD-FOA-BP模型的预测值为Y=YIMF1+YIMF2+…+YIMFn+YB。

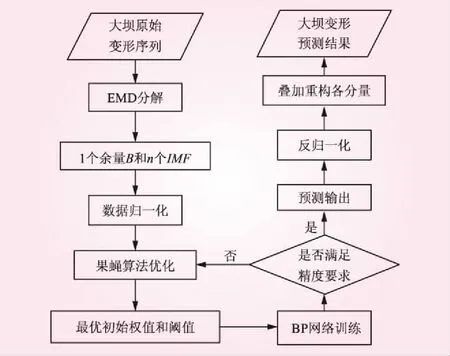
图1 EMD-FOA-BP模型预测流程

3.2 模型精度评定

本文利用平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)进行各模型预测精度评定，分别为

MAE=1n∑nt=1Yt-Y^t

(1)

RMSE=1n∑nt=1(Yt-Y^t)2

(2)

MAPE=1n∑nt=1Yt-Y^tYt

(3)

式中，Yt为实测值；Y^t为仿真所得预测值；n为观测总期数；t为观测值对应期数。

3.3 算例分析

以文献[15]中64期等时间间隔变形数据为试验数据，其变形趋势如图2所示。对大坝原始变形序列进行经验模态分解，分解结果如图3所示。

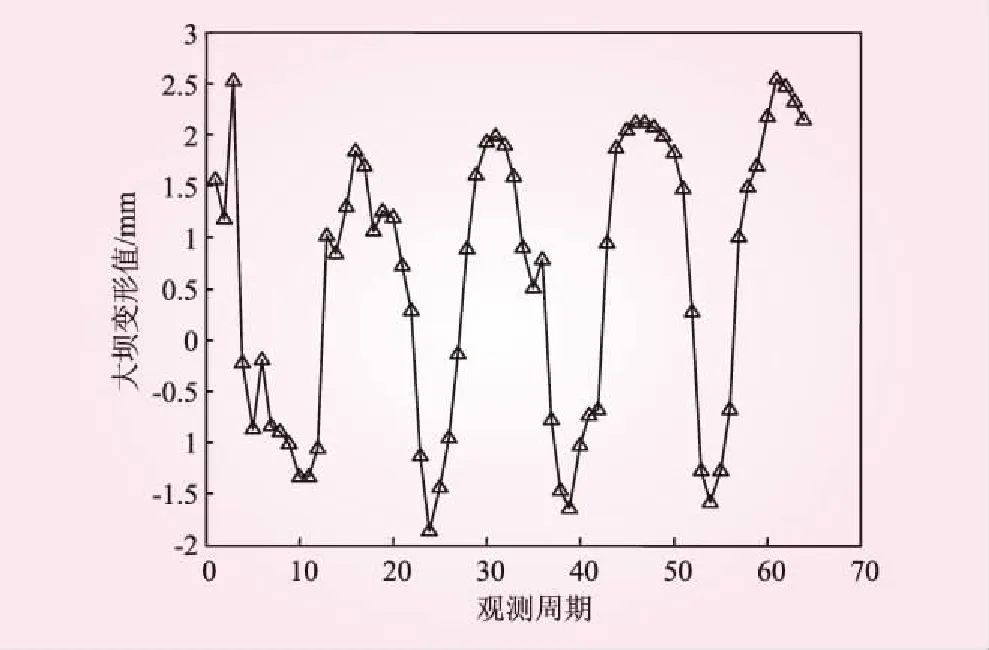
图2 大坝变形的实测值

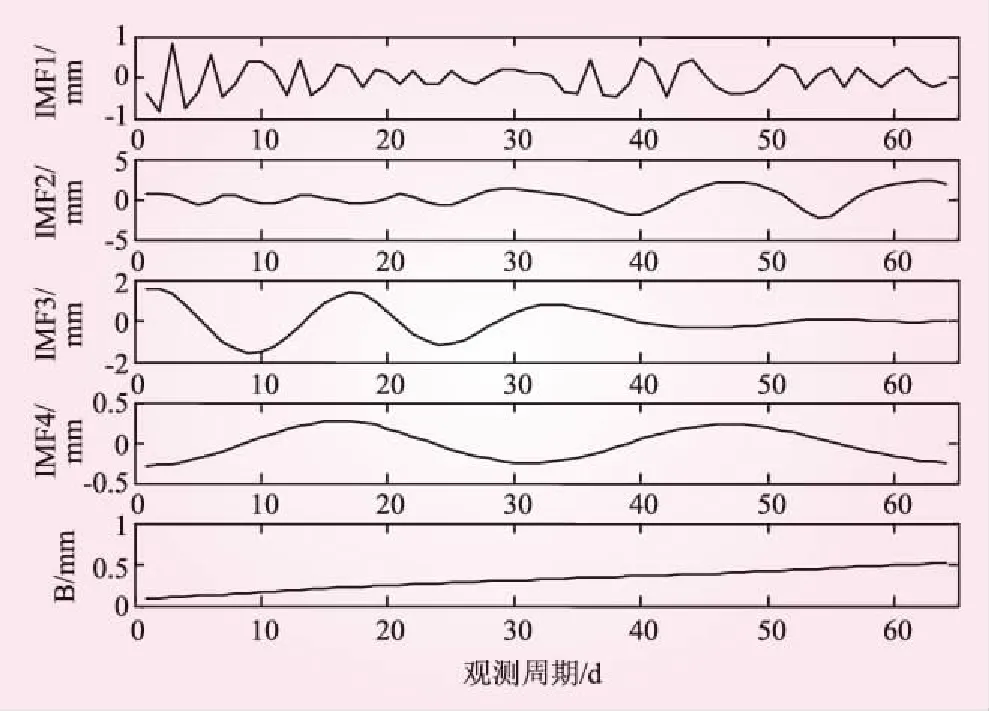
图3 EMD的多尺度分解结果

由图2的大坝变形时间序列可知，大坝变形呈明显的非平稳、非线性特征，且伴随着较强的随机性。由图3可知，利用经验模态分解方法可以把原始时间序列中的高频和低频信息量进行逐级分离，有效地分解成相对平稳的分量，便于针对分量特征分别建立预测模型。

为了验证分析本文提出模型的可行性及实用性，本文将以4种方案进行讨论，4种方案分别是①方案1，BP神经网络预测模型；②方案2，利用遗传算法优化的BP神经网络预测模型(GA-BP)；③方案3，果蝇算法优化的BP神经网络(FOA-BP)；④方案4，基于EMD和FOA-BP神经网络的预测模型(EMD-FOA-BP)。本文将前50期的大坝变形量作为以上4种方案的训练样本，后14期数据作为仿真样本。方案1至方案3未对大坝原始数据进行外部环境的平稳化处理，直接进行建模预测；方案4利用 EMD对原始序列进行分解，再将各分量分别建模预测，叠加各预测值作为最终结果。4种模型的位移实测和预测结果对比列于表1，如图4所示，残差值结果如图5所示。

由表1和图4可知，方案1中BP神经网络模型的残差序列波动较大，其中有10期残差绝对值超过0.4 mm，最大残差出现在第51期，达到0.793 5 mm；方案2的GA-BP模型预测残差序列中有4期绝对值超过0.4 mm，且都集中在预测末期，在第64期的最大残差达到1.045 4 mm。方案1、2对比可知，GA-BP模型的预测精度较方案1的BP模型有所提高，但效果不明显，且末期预测误差逐渐增大，说明其长期预测能力不足。方案3 FOA-BP模型的预测残差序列绝对值超过0.3 mm的只有第61期的0.435 5 mm，表明FOA有效克服了BP神经网络易陷入局部最优、收敛速度慢等缺点，提高了网络非线性映射能力，较方案1、2的预测精度明显提高。方案4 EMD-FOA-BP模型中预测残差序列绝对值小于0.1 mm的期数占总预测期数的78.5%，最大残差绝对值仅为0.232 7 mm，较FOA-BP模型的精度又有提高，且总体预测较为稳定，末期精度依然较高。

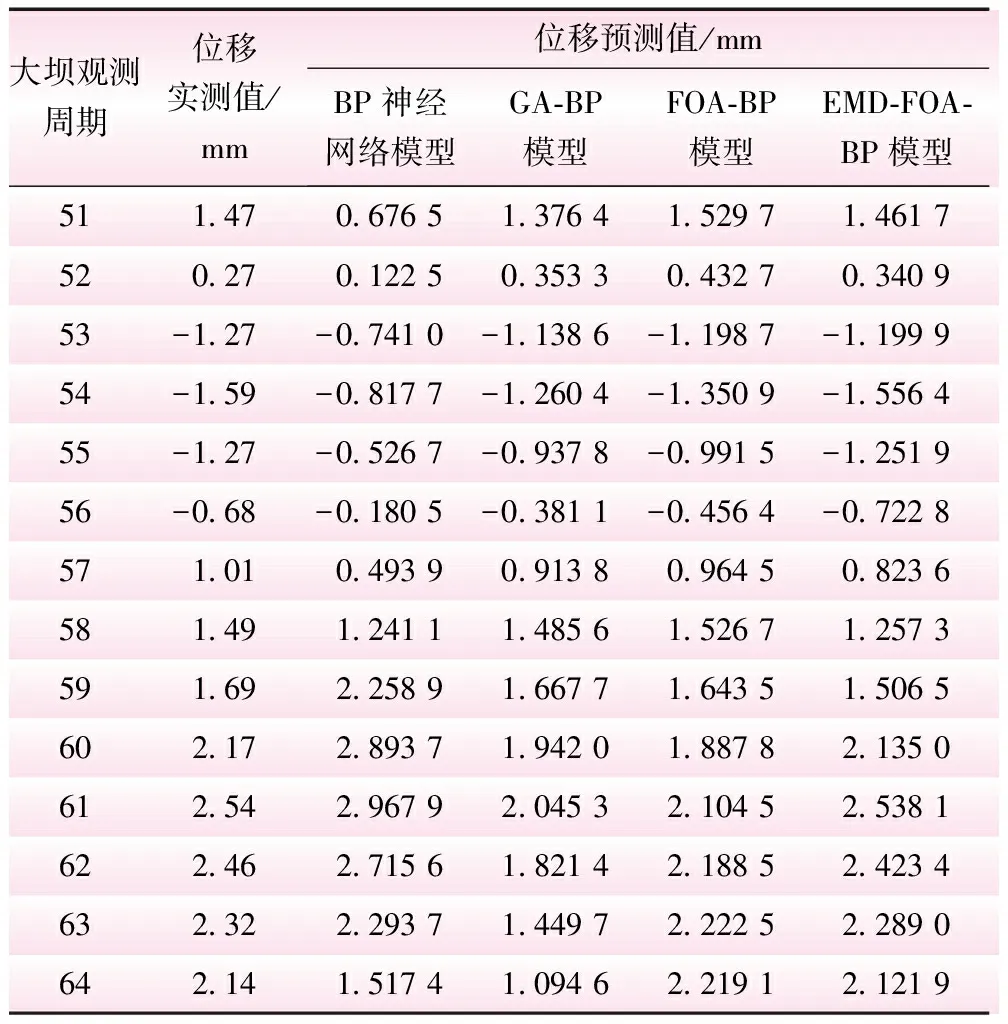
表1 4种模型的位移实测、预测结果对比

图4 4种模型的预测值和实际值对比

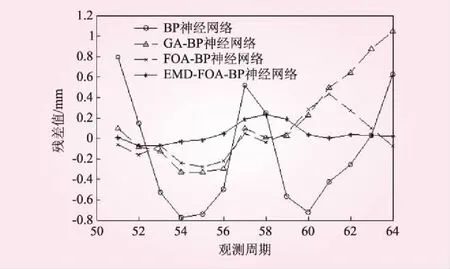
图5 4种模型的预测残差对比

由图4中各模型预测值与实际值的对比可知：BP神经网络模型预测值能够拟合实际值的变化趋势，说明该模型具有学习拟合的能力，但其精度较低，且在后期与实际值存在较大的预测误差。FOA-BP模型和GA-BP模型在预测段的前期，两者的预测精度较高，但在预测段的中后期两者均出现较大波动，预测值与实际值偏差也较大，说明模型在训练过程中学习速度跟不上原始序列的变化节奏，导致中后期仿真失效，同样说明这两个模型的长期预测能力不足。EMD-FOA-BP模型的预测值与大坝实际变形值吻合程度高，预测效果稳定，在预测段的后期仍然保持高精度预测值，说明EMD对大坝原始序列分解成相对平稳的分量，能够使模型在训练中更好的学习信号变化规则，从而提高了预测精度，且还能高精度预测更长期。

表2是4个模型的数据精度评定结果，由各项指标对比可知，EMD-FOA-BP模型预测精度最高，FOA-BP模型次之，而GA-BP模型预测精度又低于FOA-BP模型，BP神经网络模型相对最差；遗传算法与果蝇算法均能优化BP神经网络内部结构，但果蝇算法的优化效果更为显著，FOA-BP模型的均方根误差为0.204 3 mm，优于GA-BP模型的0.455 6 mm；在FOA-BP模型优势的基础上，利用EMD将大坝变形序列分解出含波动成分、周期成分、趋势成分的相对平稳分量，实现模型外部环境优化，使分量各自包含相同的变形信息，在一定程度上减少了不同特征信息之间的相互干涉，从而建立EMD-FOA-BP模型，保证了网络的局部和全局最优，其预测精度明显优于其他3种方案。

4 结 语

本文利用EMD和FOA分别对BP神经网络进行外部和内部环境优化，建立EMD-FOA-BP预测模型应用于大坝变形预测中。EMD对非线性、非平稳序列的大坝变形数据实现平稳化预处理，FOA对BP神经网络中最优权值、阈值的搜索起到明显作用，实现内部结构优化，有效克服了BP神经网络收敛速度慢、已陷入极小值等缺点，新模型增强了对非线性、非平稳函数的映射能力。实验结果表明，EMD-FOA-BP模型的预测精度优于FOA-BP模型、GA-BP模型以及BP神经网络模型。但是，由于试验数据有限，EMD-FOA-BP模型在大坝变形预测应用中的可行性有待进一步验证。