高速V型内置式永磁转子动力学分析及结构优化

谢婧萍，胡青春，麦千里，陈兴彬

(华南理工大学，广州 510640)

0 引 言

目前，永磁转子的永磁体常用排布方式有表贴式和内置式。内置式由于永磁体块内置于永磁转子铁心中，相比表贴式，其结构强度更好[1]。在高速工况下，表贴式永磁转子可通过在其外加合金热套的方法，以避免离心力对永磁转子造成损坏。Chen 等[2]分析了表贴式永磁转子的护套过盈量与转子转速的关系，并采用接触有限元法计算护套材料在各向异性和各向同性两种条件下永磁转子的结构强度，得出永磁转子的应力分布情况。但外加护套的方式会增加转子的加工难度，同时转子运行过程中护套内会产生涡流损耗，导致永磁转子温升过高[3-4]。张超等[5]利用有限元方法对传统“一”字形内置式永磁转子结构强度进行理论计算和仿真分析，建立了隔磁桥和极靴部分的受力解析模型，并通过有限元模拟进行对比验证；同时提出了永磁体分段式的结构改进方法，使永磁转子结构强度得到较大提高。V型内置式永磁转子相比传统“一”字形永磁转子，其q轴磁路更宽，磁阻更小，磁阻转矩更大，具有较好的电磁性能。张涛等[6]采用等效环的计算方法，分析了V型内置式永磁转子的结构强度，由于计算公式中修正系数a，b为经验值，需要大量的数据来确定a，b值，导致应用等效环法的解析模型复杂且精度不高。

本文应用高速离心力的产生机理对V型内置式永磁转子的受力情况进行分析，得出了各结构参数对V型永磁转子结构强度的影响公式。通过有限元模拟验证了解析法模型的正确性。相比等效环法，解析法的计算效率大大提高。基于前期研究的飞轮储能磁力耦合传动装置上的应用需求[7]，详细分析了两对极高速V型内置式永磁转子的结构特征，并利用多目标优化方法对主要的结构参数进行优化。研究结果具有一定的理论价值和实践意义。

1 V型内置式永磁转子强度理论分析

V型内置式永磁转子在额定运行工况下，其强度同时受电磁力、离心力、热应力等激励作用。在高速工况下，内置式永磁转子主要承受离心力作用，相对的电磁力、热应力则可以忽略[8]。因此，解析中仅考虑稳态运行时高速离心力对转子结构强度的影响，其他作用力对转子应力的影响在安全系数中体现。

相比传统“一”字形永磁转子，V型结构强度更优，主要是由于永磁体与极靴产生的离心力可由两个主隔磁桥和辅助隔磁桥共同承担，如图1所示。

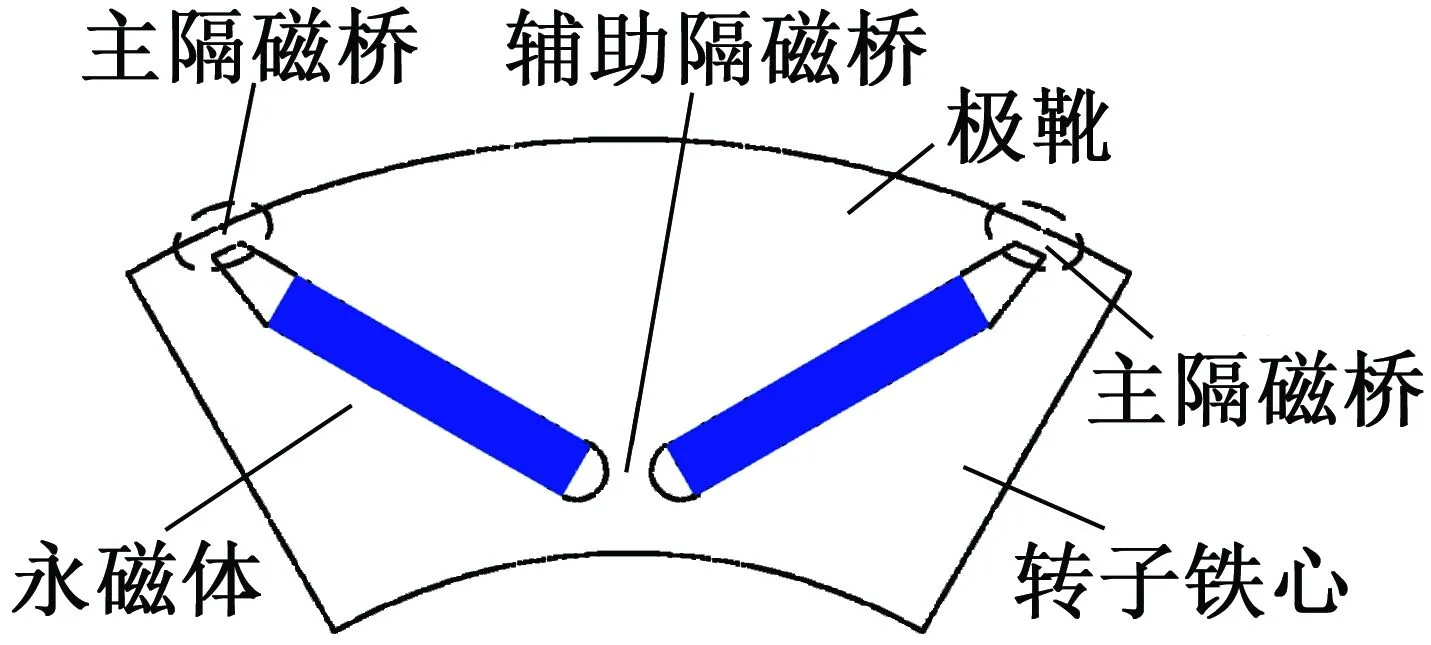
图1 V型内置式永磁转子结构示意图

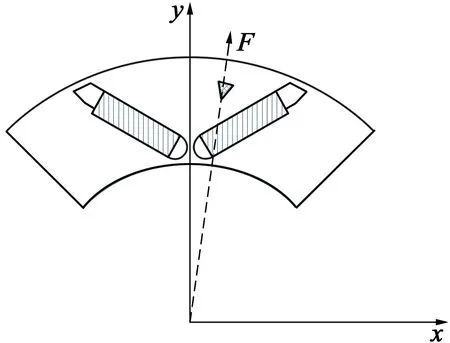
图2 转子微元体受力图

离心力方向如图 2 所示，每个微元体产生的离心力大小随作用半径变化而变化。本文引用等效半径的方法，建立简化的应力解析模型。基于离心力作用原理，假设转子在轴向方向上质量均匀分布，在x，y平面内，任意闭合曲面的质心方程可定义：

(1)

由于永磁体和极靴部件的材料差异，需分别计算各区域的离心力大小。以主隔磁桥径向厚度，将转子极靴区域划分为环形区域A1和扇形区域A2；永磁体区域一般为对称排布的矩形，形状规整，设其为A3。转子区域划分及各主要参数如图3 所示。

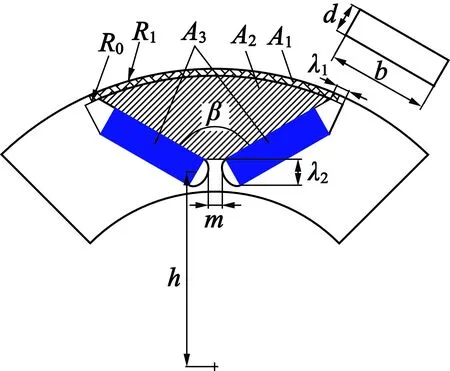
图3 转子区域划分及主要参数设置

极靴区域质心坐标：

(2)

环形区域A1对y轴的静矩与面积：

(3)

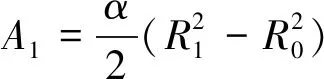
式中：R0，R1分别为环形区域A1的内、外径；α为两个主隔磁桥沿径向的夹角。

扇形区域A2对y轴的静矩与面积：

(5)

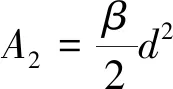
式中：b为永磁体厚度；d为永磁体宽度；m为辅助隔磁桥的切向宽度；β为V型永磁体夹角；h为永磁体靠近辅助隔磁桥的边中点到转子中心的垂直距离。

永磁体A3区域质心坐标：

(7)

永磁体区域A3对y轴的静矩与面积：

A3=2bd(9)

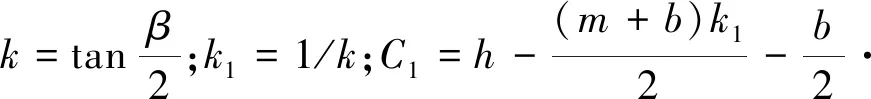
上述求解出的质心坐标即为极靴及永磁体区域的离心力等效作用半径。故根据离心力公式可求得极靴及永磁体沿y轴离心力，分别如下：

(10)

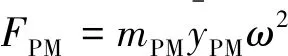
式中：mjx为极靴质量；mPM为永磁体质量；ω为转子角速度。

极靴与永磁体在y轴方向上离心力的合力F由两个主隔磁桥上的剪切应力、辅助隔磁桥上的拉伸应力承担，如图4所示。

F=Fjx+FPM(12)

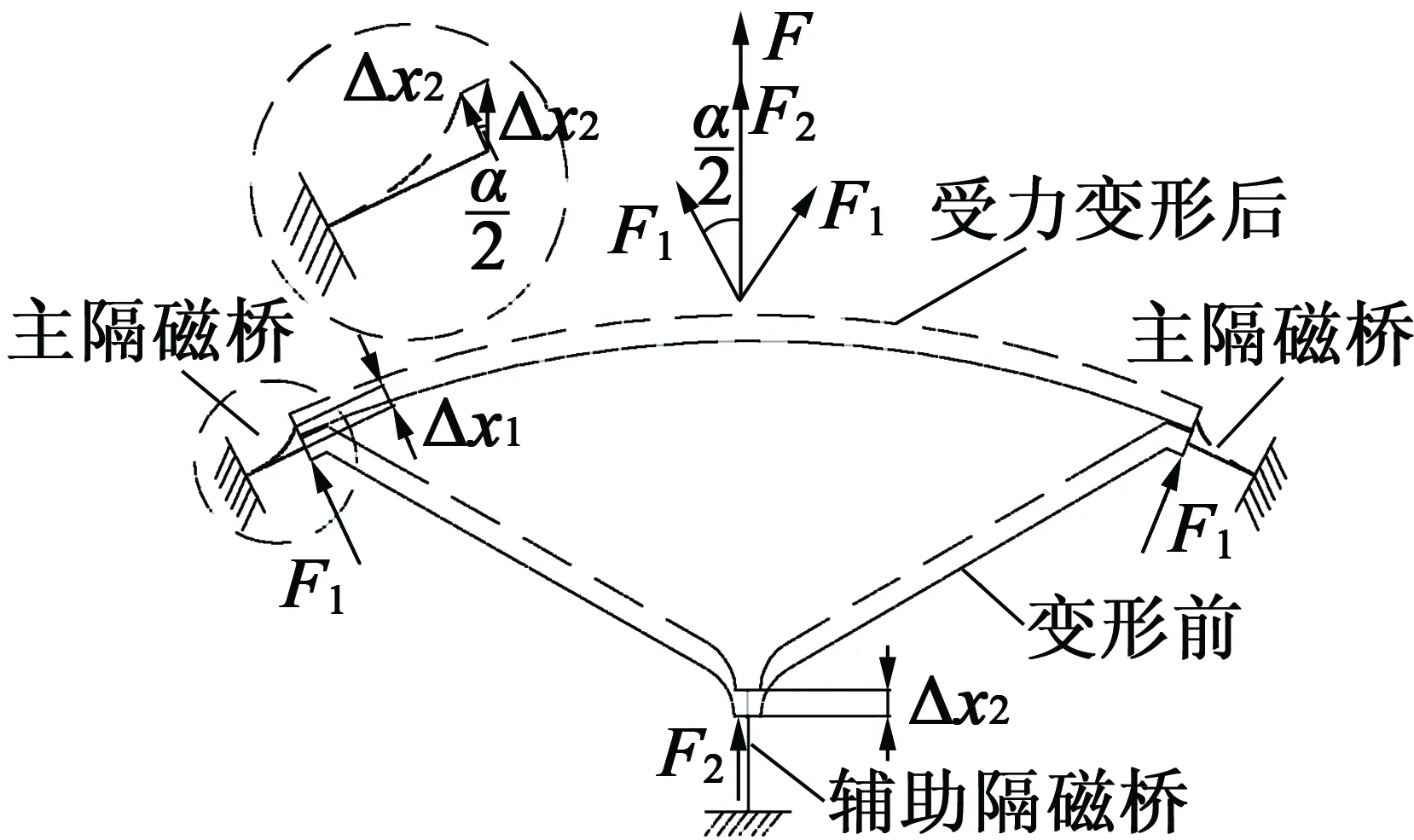
图4 转子受力分析简图

根据胡克定律、变形协调条件可建立相应关系式：

(13)

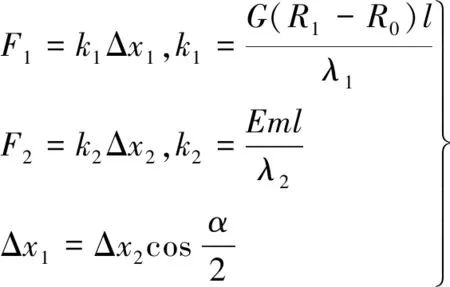
式中：F1为主隔磁桥上的剪切力；F2为辅助隔磁桥上的拉伸力；l为转子轴向长度；k1为剪切常数；k2为拉伸常数；Δx1，Δx2为主隔磁桥、辅助隔磁桥沿应变方向产生的形变位移；G为材料切变弹性模量；E为材料拉伸弹性模量；λ1为主隔磁桥的切向长度；λ2为辅助隔磁桥的径向长度。

将式(14)代入式(13)求得F1，F2：

(15)

则主隔磁桥上所受剪切应力τ、辅助隔磁桥上所受拉伸应力σ：

(16)

式中：S为应力集中系数。S的选取可参考具有环形排列圆孔的径向受力圆板模型取值[9]。根据钢结构设计规范，铁心可承受的拉伸应力远大于剪切应力，故可将拉伸应力σ作为评估转子结构强度的主要依据。

2 V型内置式永磁转子强度有限元分析

2.1 转子建模与材料属性定义

在飞轮储能磁力耦合传动装置中，磁齿轮复合电机的两对极V型内置式永磁转子与飞轮转子相连,最高转速可达30 000 r/min，且复合电机中内永磁转子与调磁转子间的内气隙设为1 mm，故要求转子的设计应满足结构强度和变形要求。

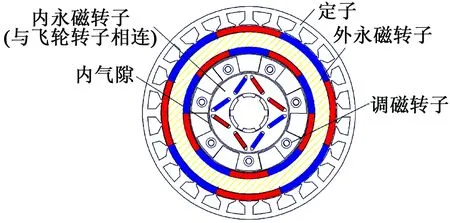
图5 飞轮储能装置中的复合电机结构

结合飞轮储能磁力耦合传动装置中对V型内置式永磁转子的设计需求和适应性条件, 初设V型内置式永磁转子结构参数如表1所示。

表1 V 型内置式永磁转子初设结构参数

极靴和转子铁心采用硅钢片DW310-35，永磁体采用高性能永磁材料NTP-320，转子各部分材料属性如表2所示。当转子高速旋转时，考虑安全系数为1.1，则转子铁心拉伸许用应力为490 MPa，剪切许用应力为294 MPa。

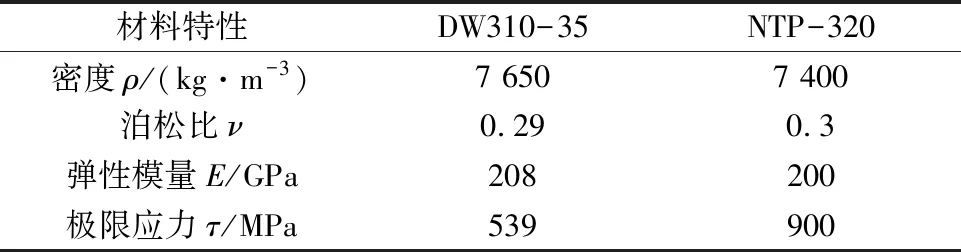
表2 永磁转子各部分材料属性

2.2 有限元分析

根据V型永磁转子的最大转速条件，利用Workbench软件计算出转子在30 000 r/min 转速下的结构强度。其等效应力、剪切应力云图如图6、图7所示。仿真值与理论计算结果相比，误差小于5%，如表3所示。

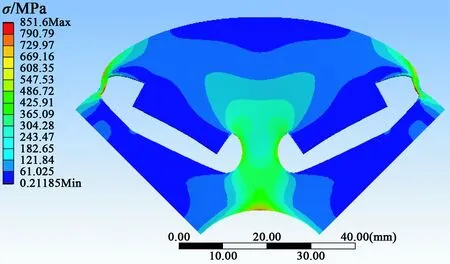
图6 转子等效应力云图

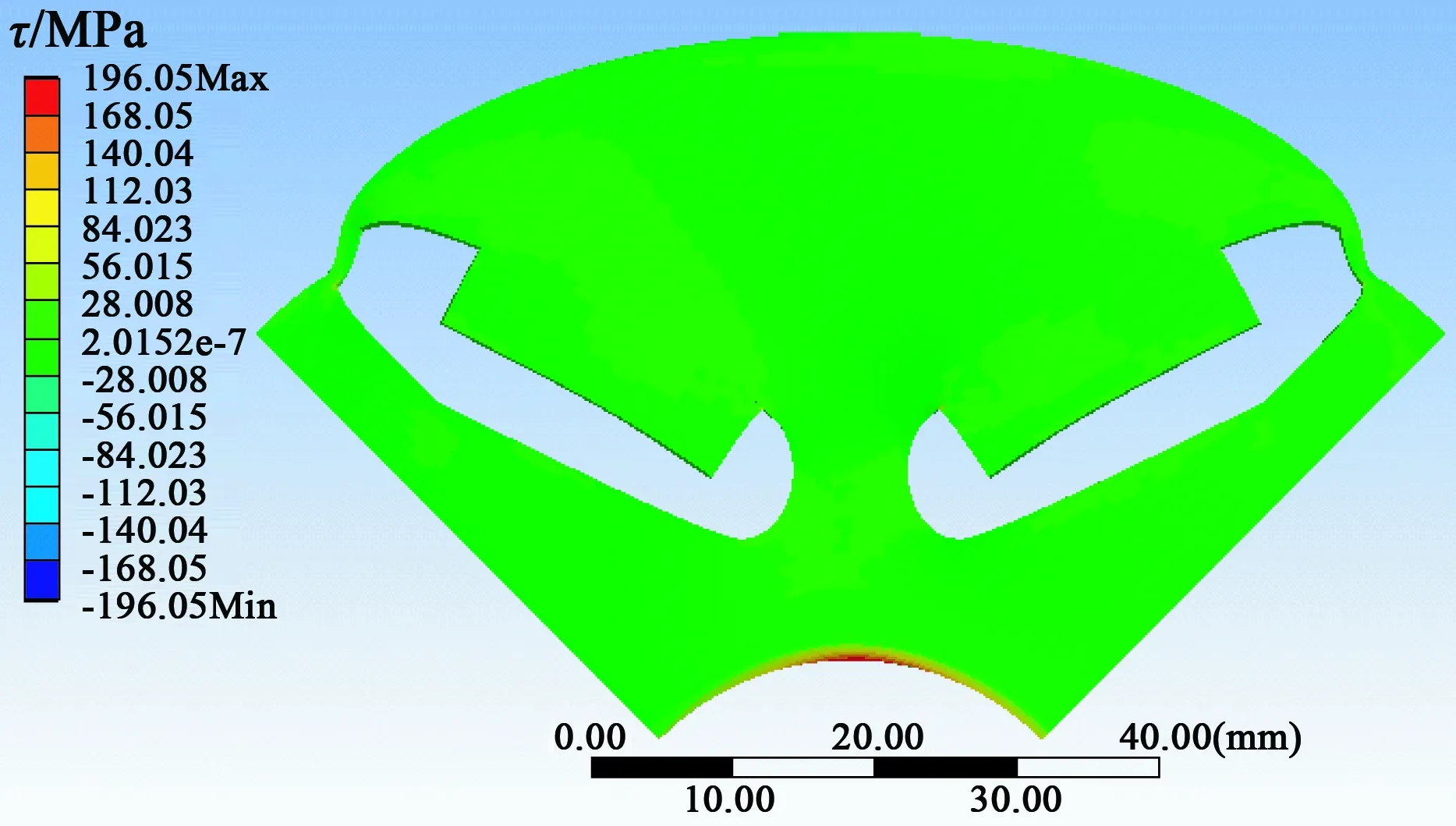
图7 剪切应力云图表3 仿真值与理论值对比

计算结果主隔磁桥剪切应力τ/MPa辅助隔磁桥拉伸应力σ/MPa理论值187.78836.45仿真值196.05851.6误差4.41%1.81%

为了进一步验证解析模型的正确性，同样基于30 000 r/min 转速条件设定R0为54 mm,55 mm,55.5 mm,56 mm,56.5 mm,57 mm(即主隔磁桥径向宽度b0分别为4 mm,3 mm,2.5 mm,2 mm,1.5 mm,1 mm)，分别采用有限元法与解析法计算了作用于转子上的最大等效应力σ，其中应力集中系数取值S=1.6。对比解析计算与有限元计算结果，二者基本吻合，误差在5%以内，如图8所示。且相比等效环法10%左右的误差，精度有较大提高。

图8 应力解析计算与有限元法对比

3 V 型永磁转子多目标优化设计

V 型内置式永磁转子拟定结构参数下计算出的最大应力为851.6 MPa，远大于转子铁心拉伸许用应力490 MPa，永磁转子的最大应力变形为0.049 2 mm，超过永磁转子在飞轮储能磁力耦合传动装置运行时允许的最大变形0.04 mm(V 型内置式永磁转子与调磁环间气隙为1 mm，其变形不允许超过气隙的4%)，故需对永磁转子的具体结构参数进行优化。

基于结构性能、电磁性能的提高，选取3个目标优化函数：① 主隔磁桥径向宽度b0，辅助隔磁桥切向宽度m对转子的漏磁影响较大，故b0，m取越小越好，体现为转子的质量越小越好；②以静应力变形量为优化目标，最大变形尽可能控制在较小的范围，以保证结构稳定性和运动可靠性；③含辅助隔磁桥转子最大应力小于并趋近许用应力，以使材料得到充分利用[10]。

3.1 响应曲面法

响应曲面法是利用合理的试验设计方法得到一定数据，采用多元二次回归方程来拟合因素与响应值之间的函数关系，通过对回归方程的分析来寻求最优参数，是解决多变量问题的一种统计方法[11]。对于有n个变量的情况下，响应面方程：

(17)

式中：X=(x1,x2,x3,…,xn)；xi(i=1,2,…,n)为设计变量；a0,aii,aij是未知系数；ε为统计误差。

3.2 设计变量选取

表征永磁转子结构设计中的8个主要参数:转子外轮廓尺寸R1，辅助隔磁桥切向宽度m，主隔磁桥径向宽度b0(b0=R1-R0)，永磁体宽度d，永磁体宽度厚度b，永磁转子轴向长度l，永磁体到转子中心的距离h，V型永磁体间夹角β，如图3所示。其中R1，d，b，l已根据设计需求确定。故提取其余尺寸m，h，β，b0作为优化参数P1～P4，如图9所示。

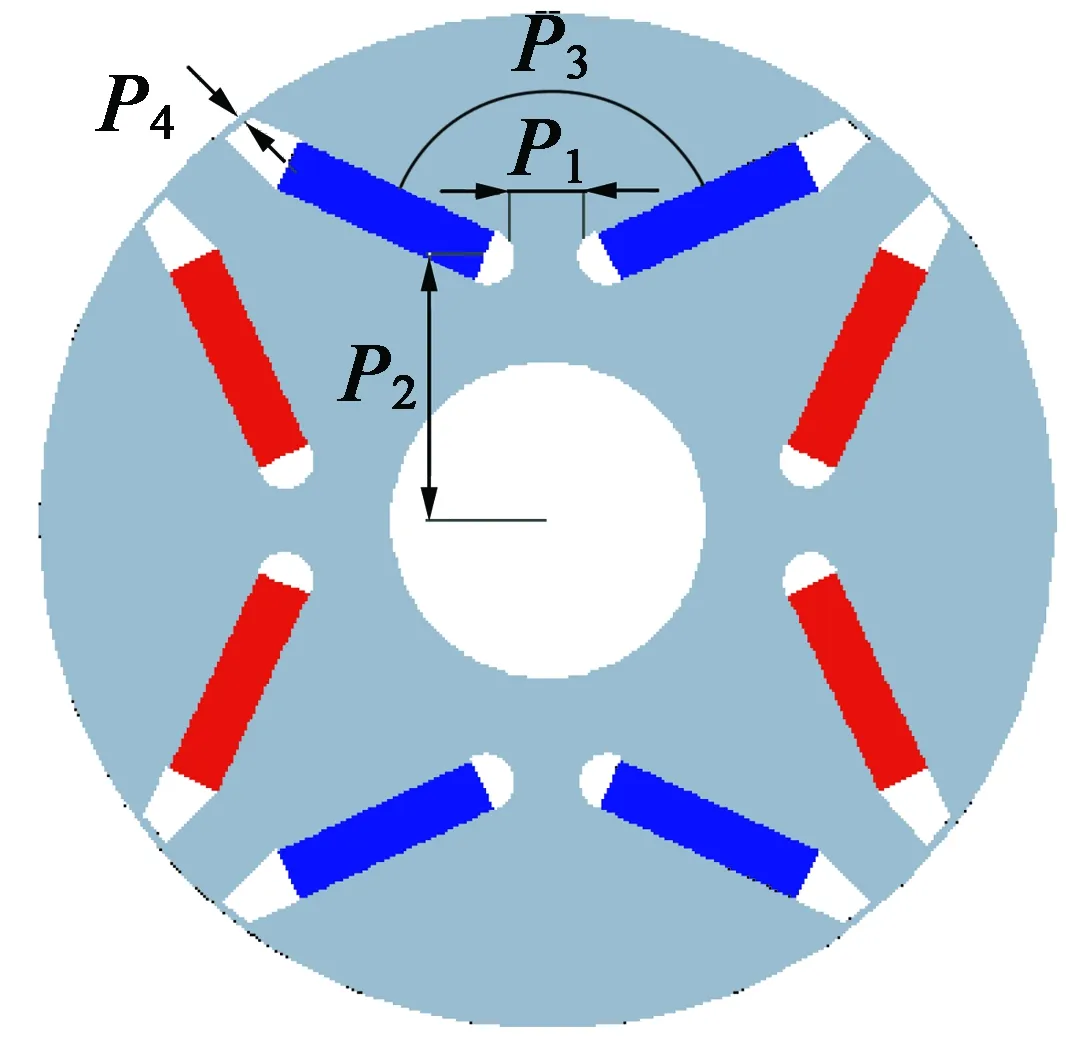
图9 设计变量的选取

3.3 多目标优化

为观察各结构参数对转子优化目标的影响，基于Workbench中Design Explorer工具对永磁转子进行优化。选取m，h，β，b0作为优化参数P1～P4，其取值范围如表4所示。

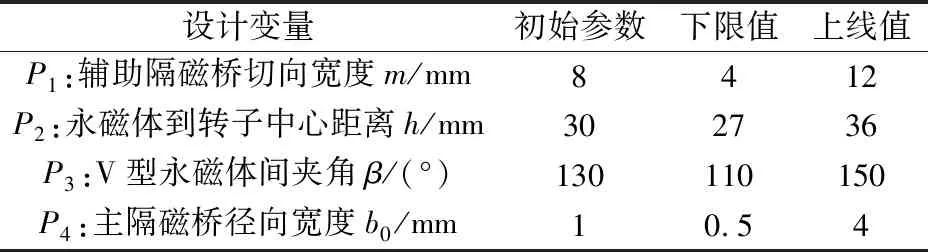
表4 永磁转子参数设置

根据性能分析拟定目标函数，以转子质量、最大变形、最大等效应力为优化目标，同时设置最大变形和最大等效应力为约束条件，即：

(18)

式中：M为转子质量；σmax为转子最大等效应力；Dgmax为转子最大变形。

通过优化分析得到永磁转子灵敏度，如图10所示，可直观表现出各设计变量对转子优化目标的影响程度。由图10可见，主隔磁桥径向宽度b0，永磁体到转子中心的距离h对转子质量影响最大；辅助隔磁桥切向宽度m对转子质量影响最小且永磁体到转子中心的距离h，辅助隔磁桥切向宽度m与质量成负相关；永磁体到转子中心的距离h对转子最大应力影响最大，其余参数影响较小。V型永磁体间夹角β，主隔磁桥径向宽度b0，永磁体到转子中心的距离h对转子变形量影响较大，且V型永磁体间夹角β，主隔磁桥径向宽度b0与转子最大变形成正相关。综上说明，在设计时应适当增加h，减小β与b0，为后期在候选设计点中寻找最佳设计点提供指导。

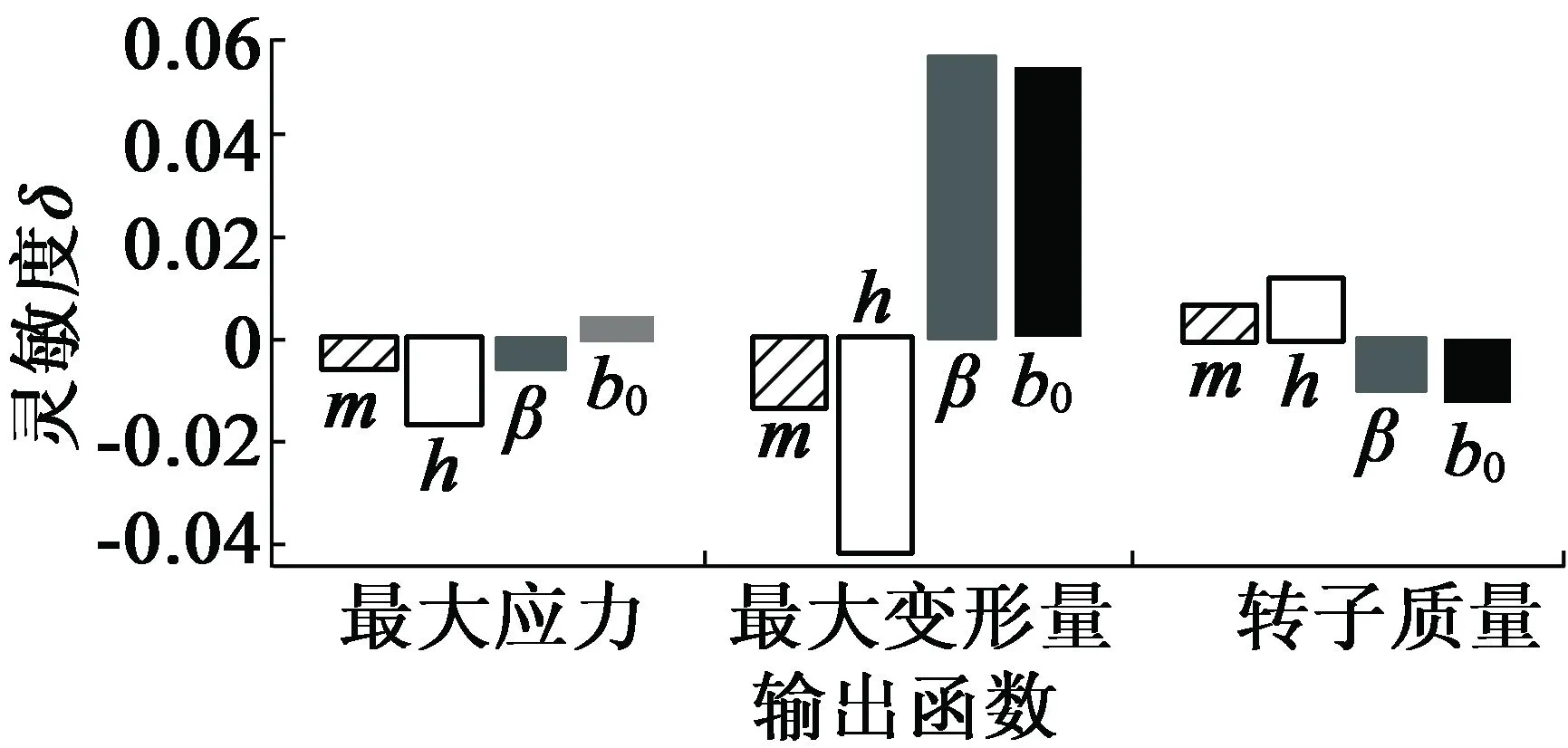
图10 V型内置式永磁转子灵敏度

通过寻优化求解，得到三组推荐候选优化设计点，如表5所示。

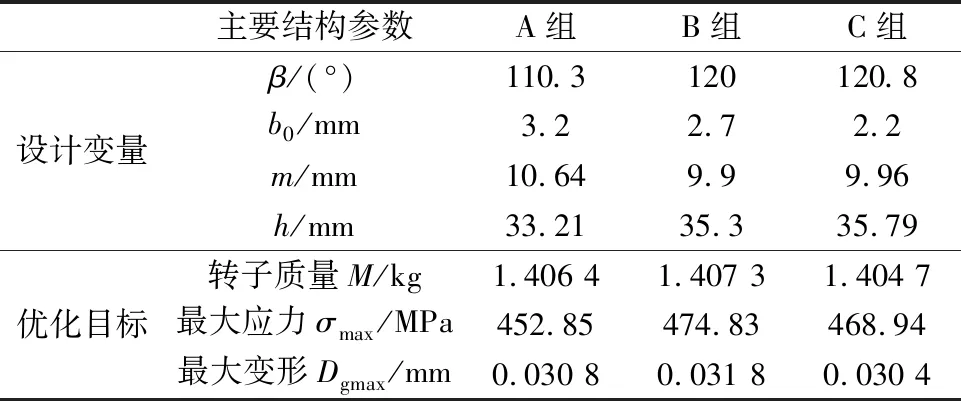
表5 三组推荐候选设计点

对比上述求解结果，C组b0最小，且m值也小于A组相应值，说明C组隔磁桥设计值更能保证较好的电磁性能；其次B组，C组的最大应力均接近于许用应力，且C组最大变形量最小，故选取C组候选点为最佳设计点，如表6所示。

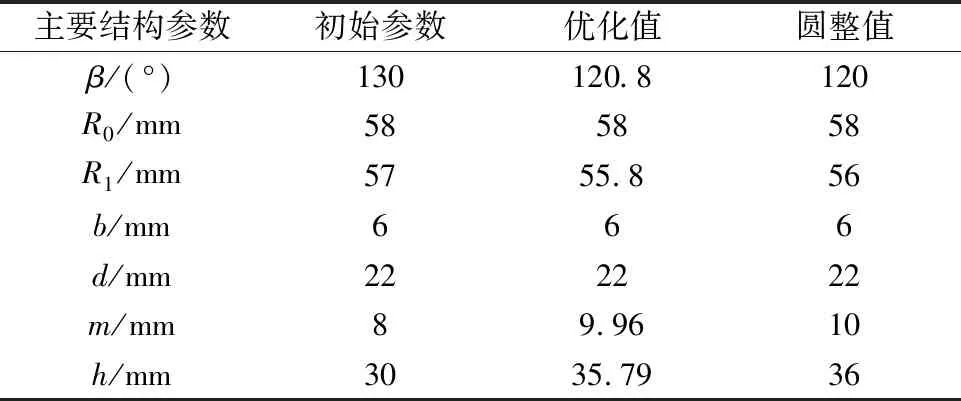
表6 V 型内置式永磁转子优化结果

4 优化有限元分析

优化后的V型内置式永磁转子模型，其等效应力、总位移云图如图11、图12所示。由图11可知，优化后的V型内置式永磁转子在高速旋转的情况下，隔磁桥处最大应力值为488 MPa，接近且小于硅钢片DW310-35拉伸许用应力，说明优化后的永磁转子在强度符合要求的情况下材料也得到充分利用。由图12可知，优化后V型内置式永磁转子的最大应力变形为0.031 3 mm，不超过永磁转子在飞轮储能磁力耦合传动装置运行时允许最大变形0.04 mm。综上，永磁转子的应力及变形符合应用要求，从而保证飞轮储能磁力耦合传动装置可靠平稳运行。

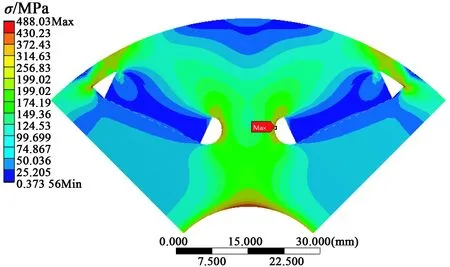
图11 V型永磁转子优化等效应力云图

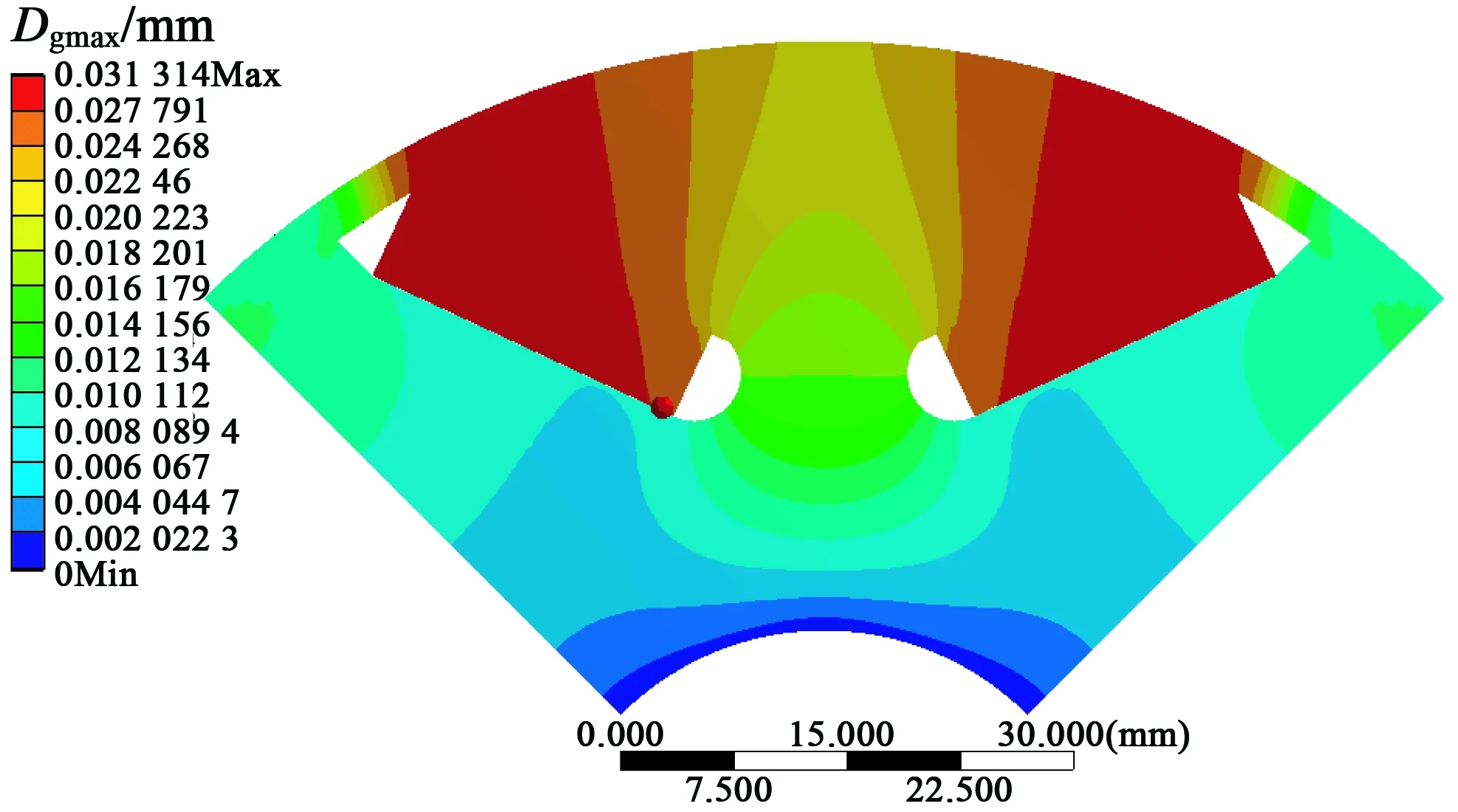
图12 V型永磁转子优化总位移云图

5 结 语

本文基于解析法与有限元法对 V型内置式永磁转子在高速转动工况下进行动力学分析，同时针对飞轮储能磁力耦合传动装置上的应用条件，详细分析了两对极高速V型内置式永磁转子的结构设计及优化思路，得出如下结论：

(1) 基于离心力、变形协调机理，推导出V型内置式永磁转子受力解析表达式，并通过有限元模拟，对比验证了解析法的正确性。相比传统等效环法需要大量试验数据确定修正系数的局限性，基于离心力的解析法计算效率更高，且解析法与有限元法的计算误差在5%以内，相比等效环法10%误差，计算精度有较大提高。为永磁转子的结构参数选择提供理论基础。

(2) 针对飞轮储能磁力耦合传动装置上的两对极高速V型内置式永磁转子，基于响应面法对永磁转子关键参数进行多目标优化分析，得到各参数对优化目标的影响效果，从而在优化设计时应适当增加h，减小β与b0，结果为高速V型内置式永磁转子的结构设计及优化提供参考。

(3) 优化后的V型永磁转子m，b0取值较小，且隔磁桥处最大应力值为488 MPa，小于且接近铁心材料拉伸许用应力，最大应力变形为0.0313mm，不超过允许最大变形0.04 mm，符合飞轮储能磁力耦合传动装置设计需求。