行波旋转型超声波电动机定转子接触滑移分析

刘 炯，纪跃波

(集美大学，厦门 361021)

0 引 言

行波型超声波电动机是利用压电陶瓷的逆压电效应，通过压电陶瓷，使定子表面产生行波，进而使定子表面质点形成椭圆的运动轨迹，在一定的预压力作用下，质点椭圆运动轨迹的切向摩擦力驱动转子周向运动。相对于电磁电机，超声波电动机具有转矩质量比大、低转速、无电磁干扰等优点，广泛应用于医疗、航天、机器人等行业[1-3]。

由超声波电动机的工作原理可知，定子振动时，接触面质点的运动轨迹是空间三维的，既有横向位移也有纵向位移和径向位移[4]。文献[5]通过增大定子与摩擦层间的摩擦因子和增大摩擦材料的泊松比来减小超声波电动机定转子间的径向滑移。文献[6]指出，转子中存在一定的阻尼有利于减少径向相对滑动造成的动力损耗，提高超声波电动机的输出效率。超声波电动机定转子之间的径向滑移造成的能量损耗是不可忽视的，研究超声波电动机结构对滑移大小的影响，有利于提高超声波电动机机械效率，减小工作时造成的能量损失[7]。以上文献都是从超声波电动机材料方向分析对接触面径向滑移的影响，本文分析超声波电动机结构对定转子接触表面质点间滑移距离的影响，选择转子腹板厚度d、定子腹板厚度k、柔性环节宽度a和柔性环节高度h四个为主要影响参数。在施加相同边界条件下，分析定转子结构参数变化对最大滑移距离的影响规律，减小定转子接触面的径向滑移，优化电机结构，提高电机输出效率。

1 转子三维建模

1.1 定转子整体结构设计

行波型超声波电动机主要由转子、摩擦层、定子和压电陶瓷组成，如图1所示。通过ANSYS进行接触仿真分析，根据定转子接触表面质点最大滑移距离，分析转子腹板厚度d、柔性部分高度h、柔性部分宽度a和定子腹板厚度k四个结构参数变化对定转子接触滑移的影响规律。在超声波电动机结构设计时，为了使定子传递更多的能量给转子，转子外径通常与定子外径相近[8-9]，本文选取定子外径60 mm、内径18 mm，转子外径59 mm、内径18 mm，摩擦片厚度0.5 mm，建立行波型超声波电动机3D结构模型，如图2所示。

(a) 定转子剖视图

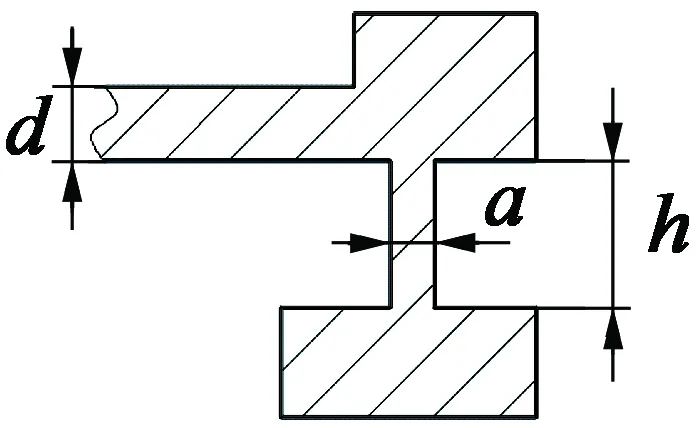
(b) A局部放大图

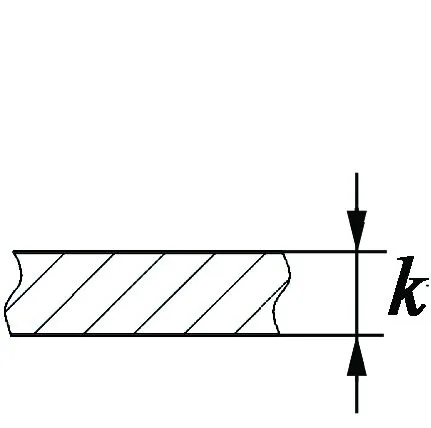
(c) B局部放大图

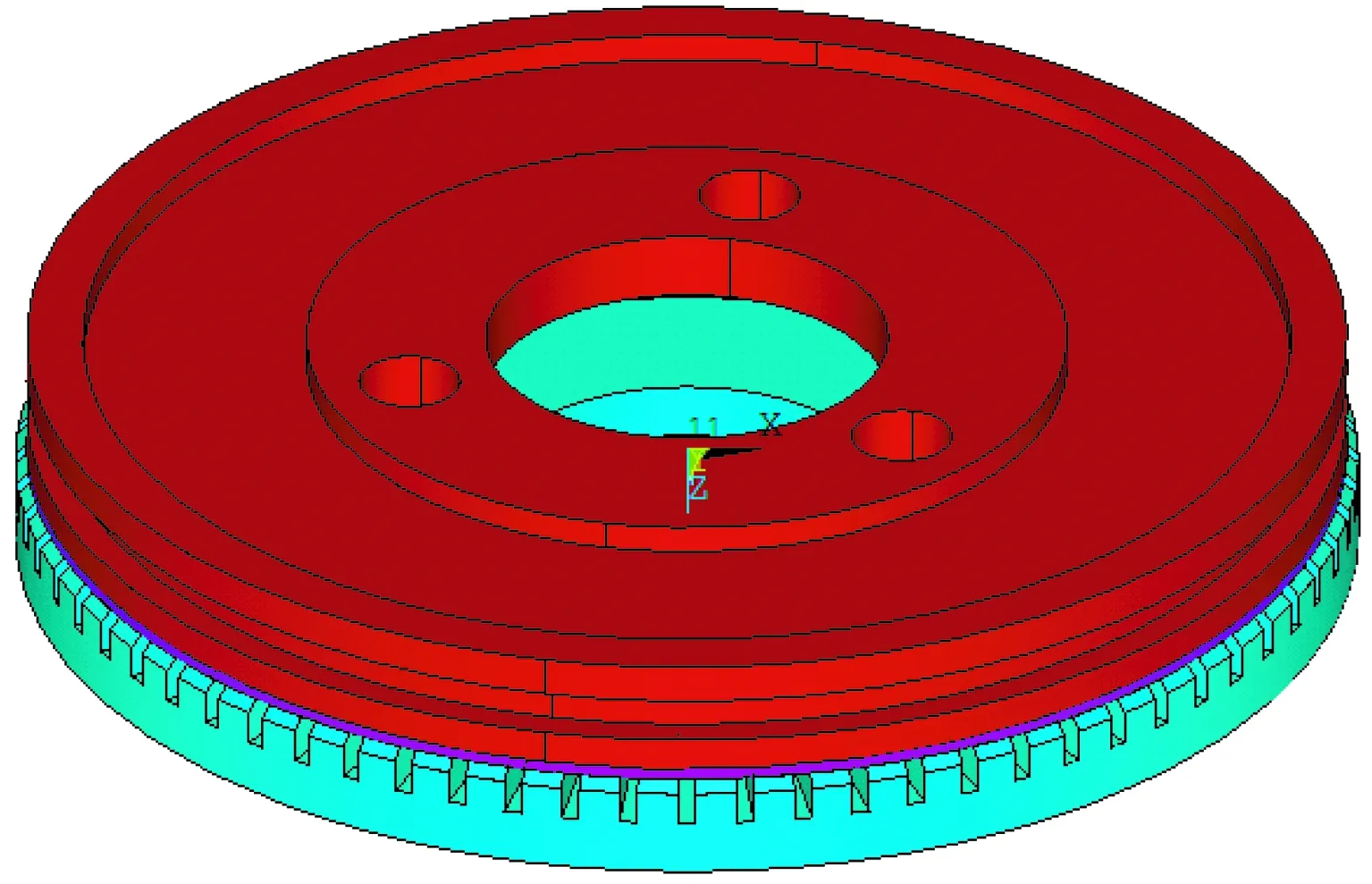
图2 定转子3D结构模型

1.2 三维模型生成

应用有限元计算软件ANSYS，建立超声波电动机的接触模型，如图2所示，选择三维20节点单元solid95对定转子进行网格划分。根据接触面接触对的设置方法，将定子表面设置为目标面，将摩擦层与定子接触的下表面设置为接触面，并设定接触对的摩擦系数为μ=0.15。根据电机工作的实际状况，对定子的螺钉孔进行全约束，对转子施加径向约束，使其不能发生平动，在转子的上表面施加预压力F=120 N，使定转子充分接触，以传递转矩。由于定子上的压电陶瓷在静态时力的作用较小，因此，忽略考虑压电陶瓷对接触应力分布产生的影响。摩擦层厚度为0.5 mm，粘接在转子表面。超声波电动机构件的材料参数如表1所示。

表1 定转子材料主要参数

2 分析与结果

各个部分参数选择如表2所示，通过分析不同结构参数对滑移距离的影响规律，为超声波电动机的优化设计提供理论基础。

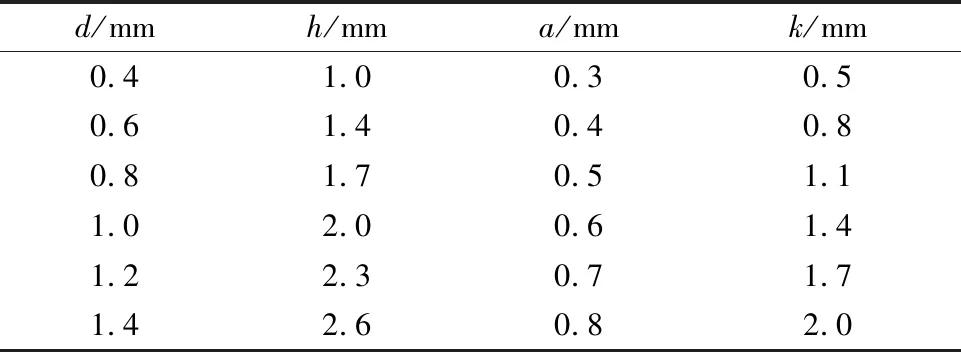
表2 电机尺寸分析选择表

2.1 转子腹板厚度和柔性部分宽度的影响分析

取柔性部分宽度a和转子腹板厚度d为变量，设定柔性部分高度h=2 mm，定子腹板厚度k=0.8 mm。接触面最大滑移距离如表3所示。

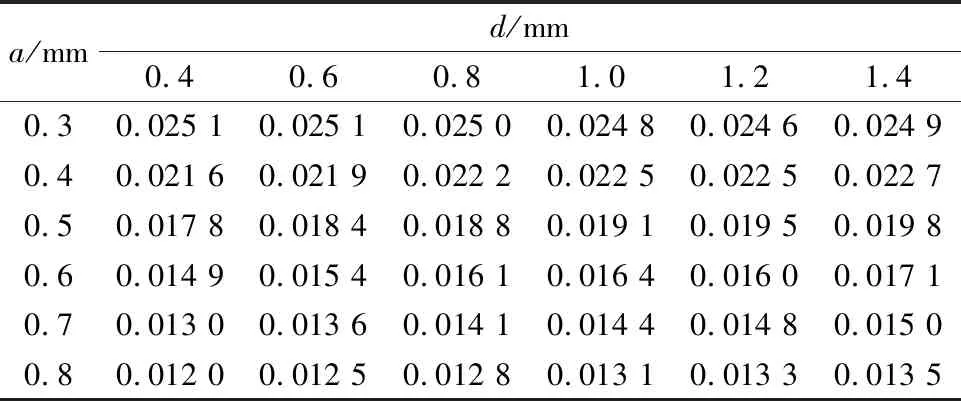
表3 不同转子腹板厚度和柔性部分宽度对应接触最大滑移距离(单位：mm)

其对应的变化曲线如图3和图4所示。

图3 不同转子腹板厚度下柔性部分宽度与滑移距离关系图

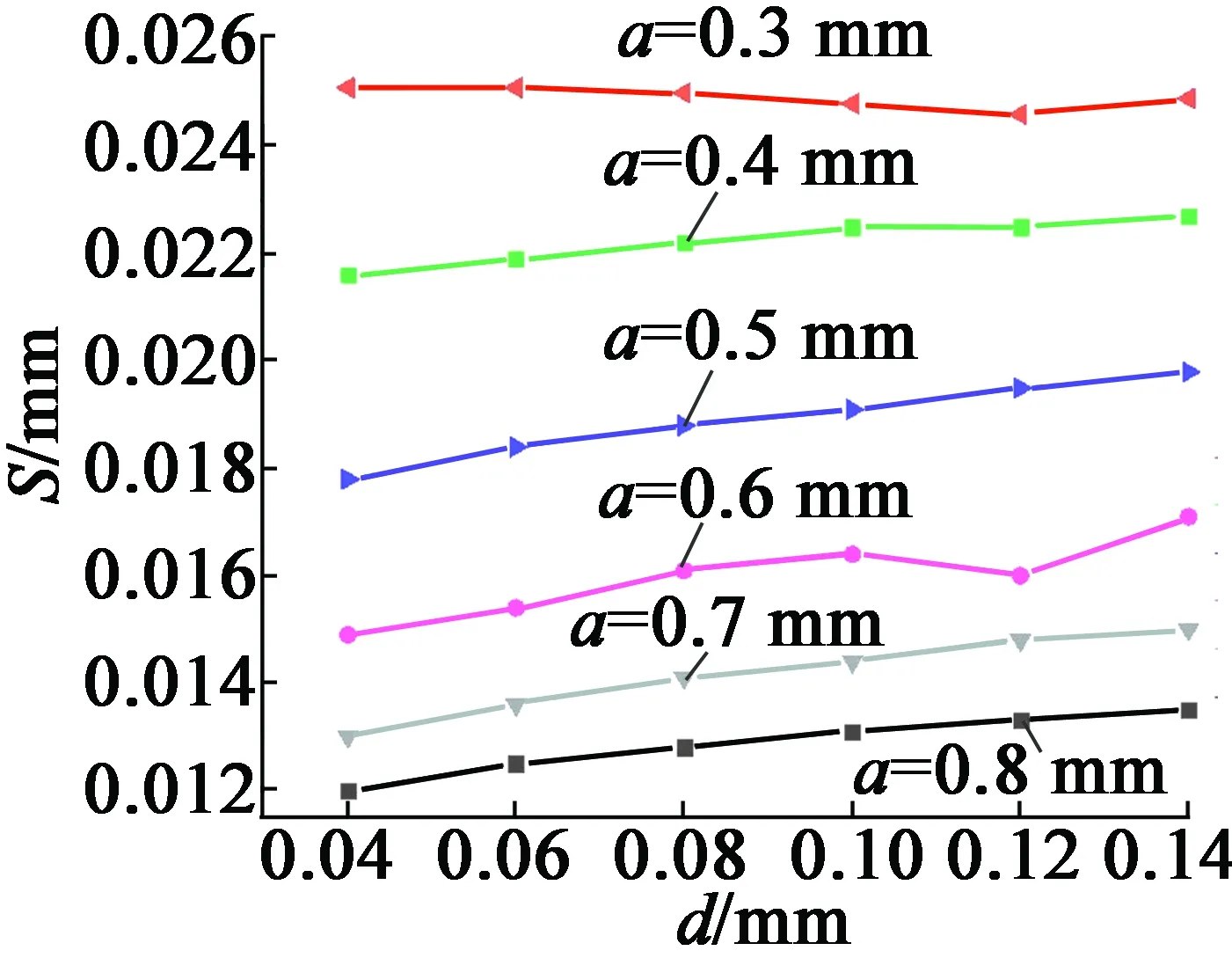
图4 不同柔性部分宽度下转子腹板厚度与滑移距离关系图

由图3可以得到，转子腹板厚度d不变时，随着柔性部分宽度a变大，滑移距离变小，且变化趋势明显；由图4可以得到，随着转子腹板厚度d变大，滑移距离变化很小。由此可知，柔性环节宽度变化对滑移距离影响较大，转子腹板厚度对滑移距离几乎无影响。

进一步分析得到如图5所示的在不同柔性部分宽度下接触滑移距离的分布情况。由定子齿表面质点振动轨迹可知，在接触区域存在径向滑移现象。由图5可得，柔性部分宽度变大，接触面积减小，使接触面磨损加剧。

图5 柔性部分宽度变化下的接触滑移分布图

2.2 转子柔性部分宽度与高度的影响分析

取柔性部分宽度a和高度h为变量，设定转子腹板厚度d=1 mm，定子腹板厚度k=0.8 mm。接触最大滑移距离结果如表4所示。

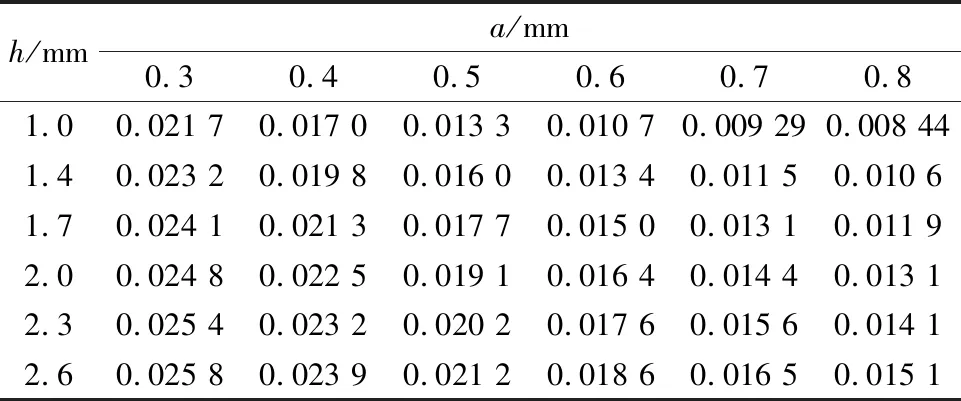
表4 不同柔性部分宽度和高度对应接触 最大滑移距离(单位：mm)

其对应的变化曲线如图6和图7所示。

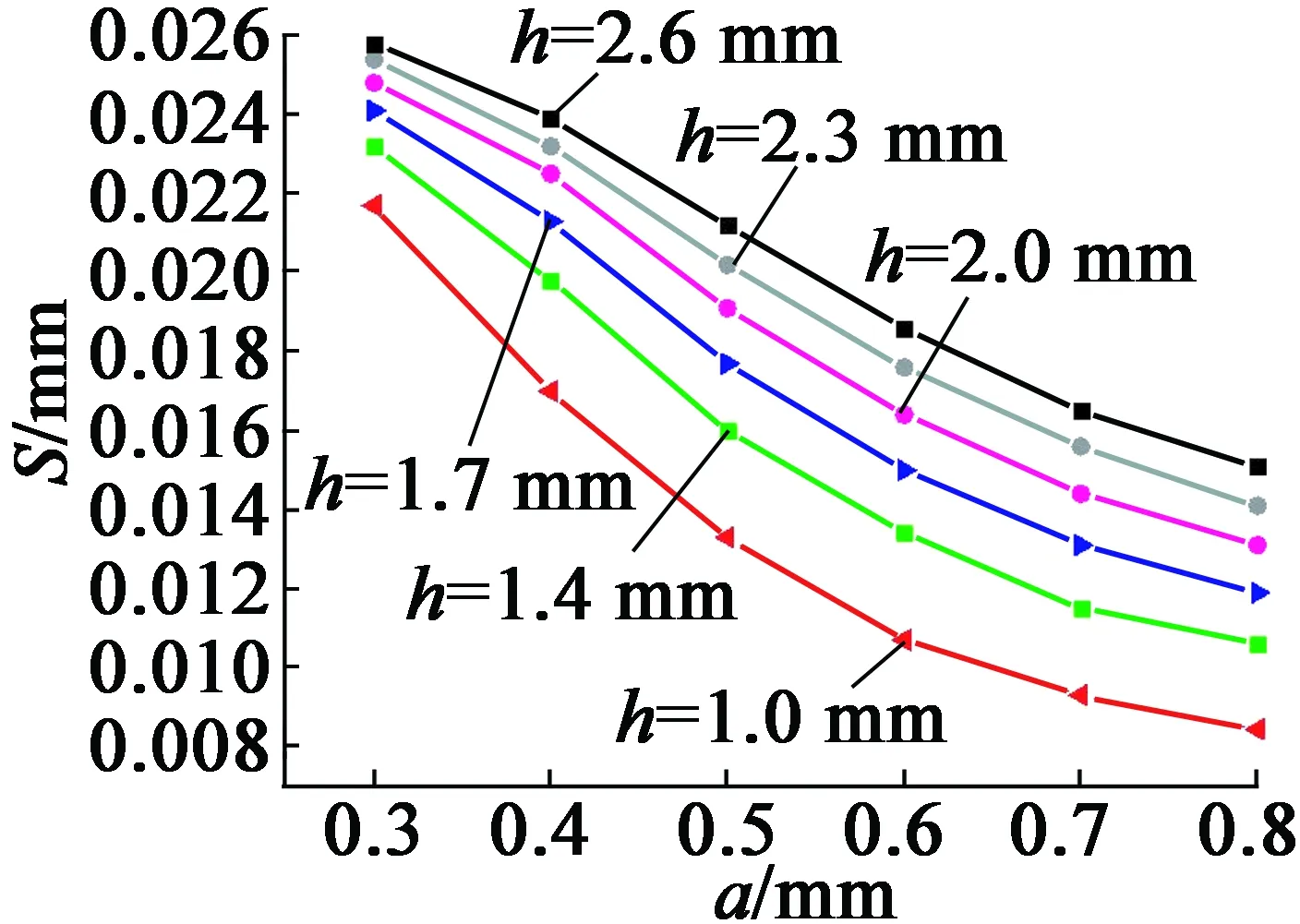
图6 不同柔性部分高度下柔性部分宽度与滑移距离关系图

图7 不同柔性部分宽度下柔性部分高度与滑移距离关系图

由图6可以得到，随着柔性部分宽度a变大，接触滑移距离变小；由图7可以得到，随着转子柔性环节高度h变大，滑移距离变大。由此可知，柔性环节宽度变化对滑移距离影响较大，柔性部分高度变化对滑移距离影响较小。

进一步分析得到如图8所示的在不同柔性部分宽度下接触滑移距离的分布情况。由图8可知，柔性部分高度的变化，对定子和转子接触面积影响较小。

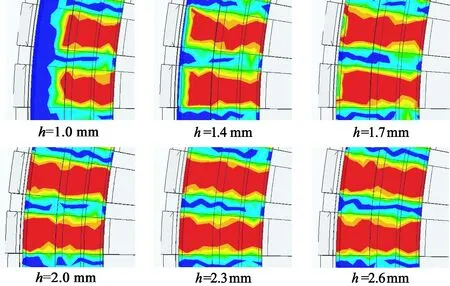
图8 柔性部分高度变化下的接触滑移分布图

2.3 定子腹板厚度与柔性环节宽度的影响分析

取柔性环节宽度a和定子腹板厚度k为变量，设定转子腹板厚度d=1.0 mm，柔性环节高度h=2.0 mm。接触面最大接触应力结果如表5所示。

表5 不同定子腹板厚度和柔性环节宽度 对应接触最大滑移距离(单位：mm)

其对应的变化曲线如图9和图10所示。

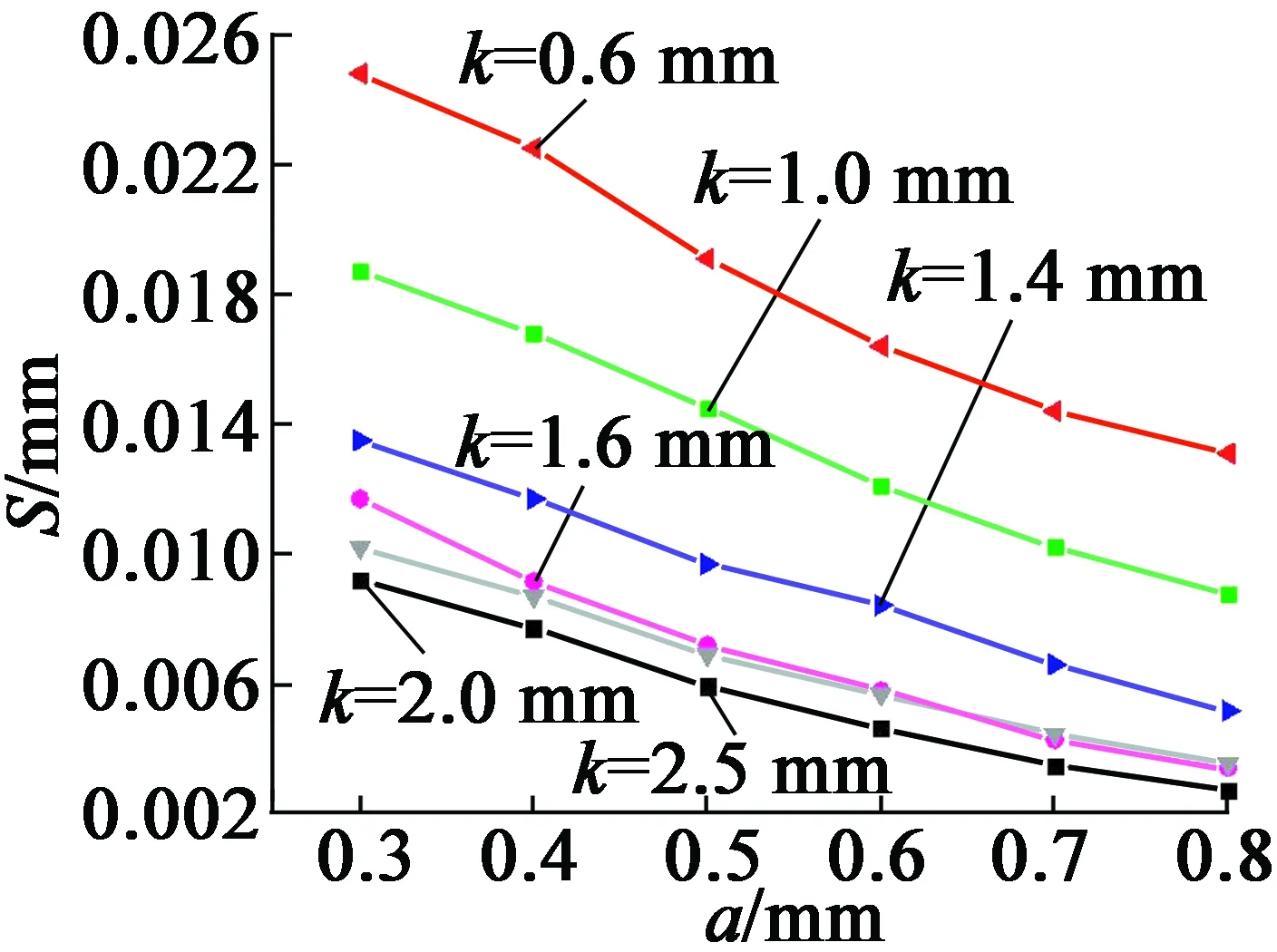
图9 不同定子腹板厚度下柔性环节宽度与滑移距离关系图

图10 不同柔性环节宽度下定子腹板厚度与滑移距离关系图

由图9可得，定子腹板厚度不变时，柔性环节宽度变大，滑移距离变小；由图10可得，柔性环节宽度不变时，定子腹板厚度变大，滑移距离变小，且当定子腹板厚度增大到一定时，滑移距离变化量逐渐减小。由此可知，定子腹板厚度变化对滑移距离影响较大。

进一步分析得到如图11所示的在不同柔性部分宽度下接触滑移距离的分布情况。由图11可知，定子腹板厚度变大，接触面积先减小后变大。

3 结 语

本文根据对超声波电动机整体结构四个尺寸参数在相同边界条件下对接触滑移距离的仿真分析，可以得出：电机转子腹板厚度d的变化对接触面滑移距离几乎无影响；柔性环节高度h对接触滑移距离影响较小，柔性环节高度越大，滑移距离越大；柔性环节宽度对接触面滑移距离影响较大，且柔性环节宽度越大，滑移距离越小；定子腹板厚度对接触面滑移距离影响最大，定子腹板厚度越大，滑移距离越小。柔性部分宽度和定子腹板厚度对定子和转子接触面积影响较大。故在设计时结合超声波电动机定转子结构对接触面滑移距离影响规律，合理选择结构参数，提高超声波电动机输出效率。