采用自适应扰动观察法的光伏并网系统最大功率点跟踪

谢 维，饶国勇2，蔡建羨，李立新，陈 逊

(1.防灾科技学院 电子科学与控制工程学院，河北 三河 065201； 2.景德镇学院，江西 景德镇 333000)

0 引言

全球的电力需求和消费正在快速增长。可再生能源由于其清洁性、低成本和获取方便等优点，近年来得到了迅猛的发展。在太阳能、风能、海洋潮汐能等可再生能源中，太阳能是一种目前最成熟和有商业前景的发电能源。可以使用光伏(PV)效应从太阳光以产生电力[1]，这种技术广泛用于为独立负载或电力系统供电。然而，可以看到太阳能光伏电池的转换效率非常低，仅为9%到17%，尤其是在低太阳照射条件下。另外，太阳能PV板产生的电力总是在各种天气条件下变化。很显然，太阳能光伏电池的V-I和V-P特性是非线性的，随照射量和温度而变化[2]。然而，V-I或V-P曲线上始终存在一个称为最大功率点(MPP)的独特点。这一点在这些特性上是未知的，但它可以通过MPPT算法定位，一般分类如下：扰动观察(P&O)法[3-5]，增量电导(InC)法[6-8]，恒定恒流(CC)或恒定电压(CV)法[9-10]等算法以及其他一些诸如模糊逻辑(FL)法[11-12]，人工神经网络(ANN)法[13]和粒子群优化(PSO)法[14-15]等算法。这些现有算法在简单性、收敛速度、额外的硬件和成本等方面各有优缺点。本文提出了一种适用于太阳能光伏并网系统MPPT的自适应扰动观察算法。与采用扰动观察算法的结果相比，所获得的仿真结果证实了所提算法的有效性和优越性。本文的各部分安排如下：太阳能光伏电池板的数学模型、太阳能光伏并网系统放在第1节、第2节中描述；第3节介绍了MPPT策略的自适应扰动观察算法；然后根据仿真结果在第4节中证实所提算法的有效性；最后通过与现有的扰动观察相关算法的比较，总结了新方案的优点。

1 太阳能光伏电池板的数学模型

太阳能光伏电池板可以用如下的方程组来描述：

(1)

(2)

(3)

式中，I为太阳能光伏电池的电流(A)；V为太阳能光伏电池的电压(V)；P为太阳能光伏电池的功率(W)；Isc为太阳能光伏电池的短路电流(A)；Voc为太阳能光伏电池的开路电压(V)；I0为二极管反向饱和电流(A)；q为元电荷电荷量，q=1.602×10-19(C)；k为波尔兹曼常量，k=1.381×10-23(J/K)；T为太阳能光伏电池板的温度(K)。

太阳能光伏电池板板对阴影非常敏感。因此，我们提出了一种更准确的太阳能光伏电池的等效电路，以考虑阴影的影响，以及由于模块内部的串联电阻，触点以及单元与模块之间的互连所引起的损耗。那么，太阳能光伏电池板的V-I特性可以改写如下：

(4)

式中，Rs和Rp分别为：考虑了阴影与损耗影响后的电阻值。

尽管，制造商们正试图最小化这两种电阻值的影响，以改善他们的产品性能，然而那种理想的情况是不可能实现的。

不得不指出的V-I特性的两个重点是，开路电压Voc，以及短路电流Isc。在这两点时所发出的功率均为零点。当电池的输出电流I为零(I=0)时，Voc就被确定下来了；而当电池的输出电压V为零(V=0)时，Isc就被确定下来了。在电池的V-I特性上的乘积(V×I)为最大的点处，太阳能光伏电池发出的功率最大。这一点被称为最大功率点(MPP)，并且它是独一无二的。

显然，在太阳能光伏电池板的发电中必须考虑的两个重要因素是照射量和温度。这些因素强烈影响太阳能光伏电池板的特性。因此，MPP点在白天会发生变化。如果工作点不接近MPP，则会发生显著的功率损耗。那么，必须在各种条件下跟踪MPP点，以确保从太阳能光伏电池板处获得最大的可用功率。通过在各种条件下搜索和确定MPP点，将这一问题交给了最大功率点跟踪(MPPT)算法。本文提出了自适应扰动观察算法，来用于搜索MPP点，下面将详细介绍。

2 太阳能光伏并网系统

太阳能光伏系统可分为两种类型：需要电池来存储能量的独立太阳能光伏系统，以及用于大功率应用场合的太阳能光伏并网系统。太阳能光伏并网系统主要由以下部件组成，包括太阳能光伏电池阵列，DC / DC变流器，DC / AC逆变器，滤波器，变压器和储能系统等，如图1所示。

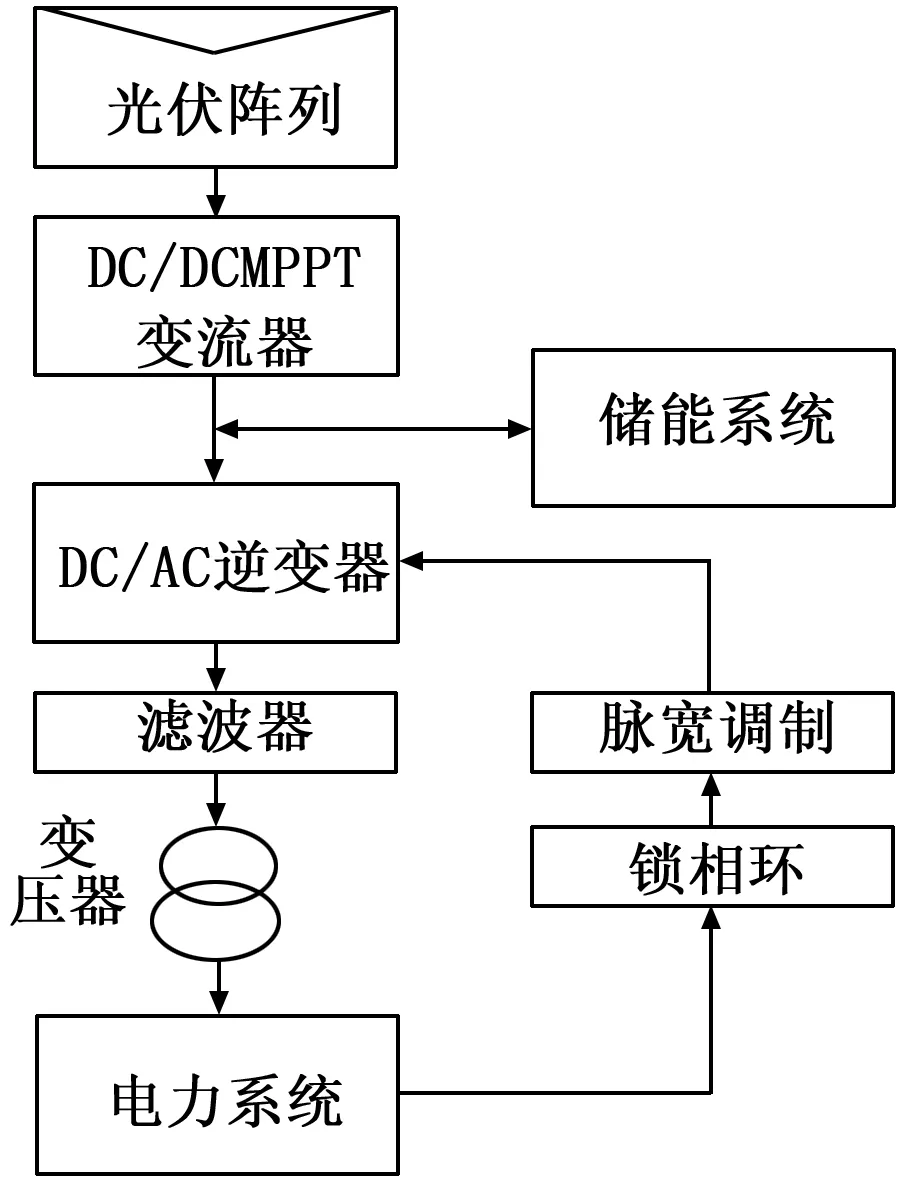
图1 太阳能光伏并网系统结构图

DC / DC变流器主要用于将来自电压波动的电源，调节输出电压为恒定值，以减小输出电压中的纹波；也可以从同一的输入电压等级，获得多个电压等级。DC / DC变流器有包括buck(降压)，boost(升压)和buck-boost(升降压)的多种拓扑结构。另外，DC / AC逆变器主要用于将恒定的直流电压，转换成具有可变的幅值和频率的三相交流电压，其是通过利用脉冲宽度调制(PWM)技术控制半导体开关器件来实现。锁相环(PLL)则通过求解电网电压的abc分量，在公共耦合点提供旋转频率，直接和正交电压分量。

3 采用先进的扰动观察算法的光伏并网系统MPPT

扰动观察算法的基本原理是每隔一定的时间，增加或者减少太阳能光伏电池阵列的输出电压，这一过程称为“扰动”，并观测之后其输出功率变化方向，若ΔP>0，说明参考电压调整的方向正确，可以继续按原来的方向“扰动”；若ΔP<0，说明参考电压调整的方向错误，则需改变“扰动”的方向。我们知道，扰动观察算法通常采用固定的步长，导致在快速变化的天气条件下，跟踪MPP点发生失败。可以通过在不同的天气条件下，采用可变步长来克服这个缺陷。因而本文提出了自适应的扰动观察算法。

假设在这种传统扰动观察算法中的扰动变量，是太阳能光伏电池板端电压的参考值。因此，如果输出太阳能光伏电池板的电压被扰动，且dP/dV>0，那么就可以知道工作点位于最大功率点MPP的左侧。扰动观察算法因而会增加太阳能光伏电池板的参考电压，以便将工作点移向MPP点。又或者，如果太阳能光伏电池板的输出电压受到扰动，且dP/dV<0，那么就可以知道，工作点位于MPP点的右侧。扰动观察算法即会降低太阳能光伏电池板的参考电压，便将工作点移向MPP点。该过程在图2和表1中更清楚地描述出来。

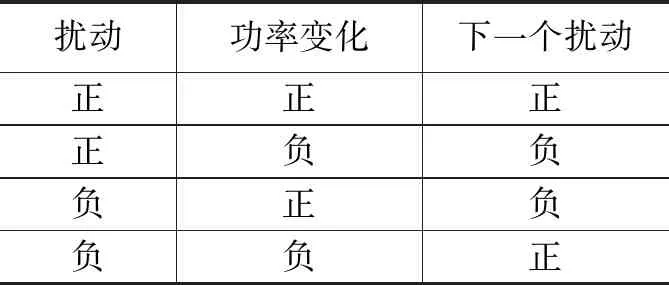
表1 传统的扰动观察算法总结

图2 传统的扰动观察算法的工作原理图

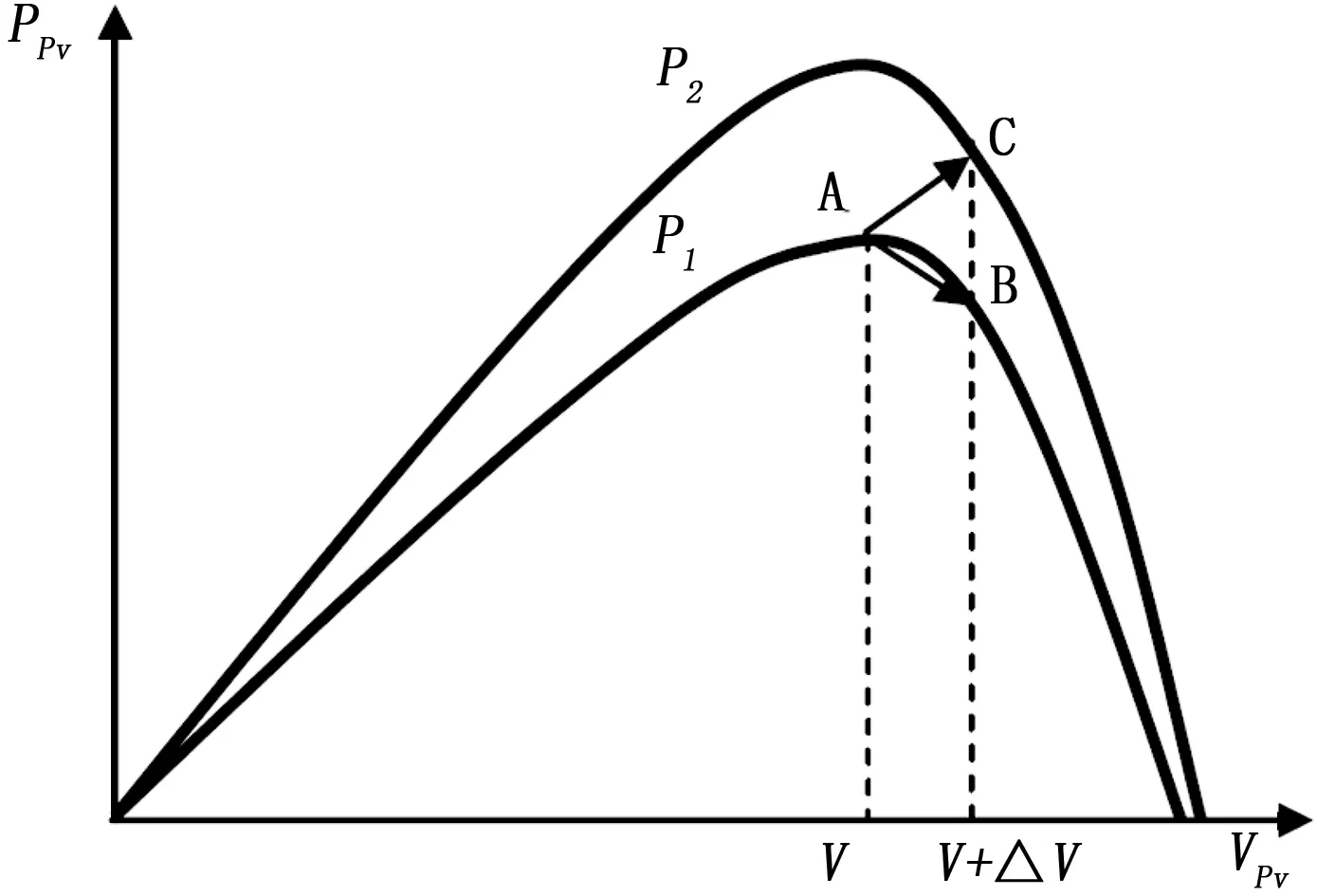
图3 传统的扰动观察算法引起最大功率点误判的原理图

我们可以周期性地重复该过程，直到达到MPP点。不过，我们知道传统的扰动观察算法在不同天气之间快速变化的情况下，容易发生失败，导致如图3所示的误判发生。假设它是从一个工作点A开始的。如果天气条件近似恒定，那么一个太阳能光伏电池板电压V的扰动ΔV，将把工作点移动到B点，并且扰动将被反转，由于功率下降了。但是，如果太阳光照射量增加了，并且在一个采样周期内，功率曲线从P1曲线转移到了P2曲线，工作点则将从A点移动到C点，这代表功率增加，因而扰动的方向将保持不变。

结果是，工作点将偏离最大功率点MPP，并且如果太阳照射稳定增加，将一直持续偏离下去[16]。为了确保在太阳照射量的突然变化的情况下，能跟踪到MPP点，提出了一种自适应扰动观察算法，即取决于功率变化的可变的扰动步长。这意味着扰动步长变化，并且连续调节，以适应变化的天气条件。这种自适应扰动观察算法，是传统的扰动观察算法的一种变体，可以减少通常与扰动观察相关的主要缺陷，诸如收敛速度和跟踪效率等。该扰动步长变量取决于功率的改变，如下式所示：

(5)

4 仿真结果与分析

采用Matlab / Simulink软件，可以获得将太阳能光伏系统连接到电力系统时，其MPPT控制策略的仿真结果。太阳能光伏系统配置为由10块串联再2串并联的共20块电池板排列构成。太阳能光伏系统的规格和参数如表2所示，电网电压和频率分别为220 V和50 Hz。

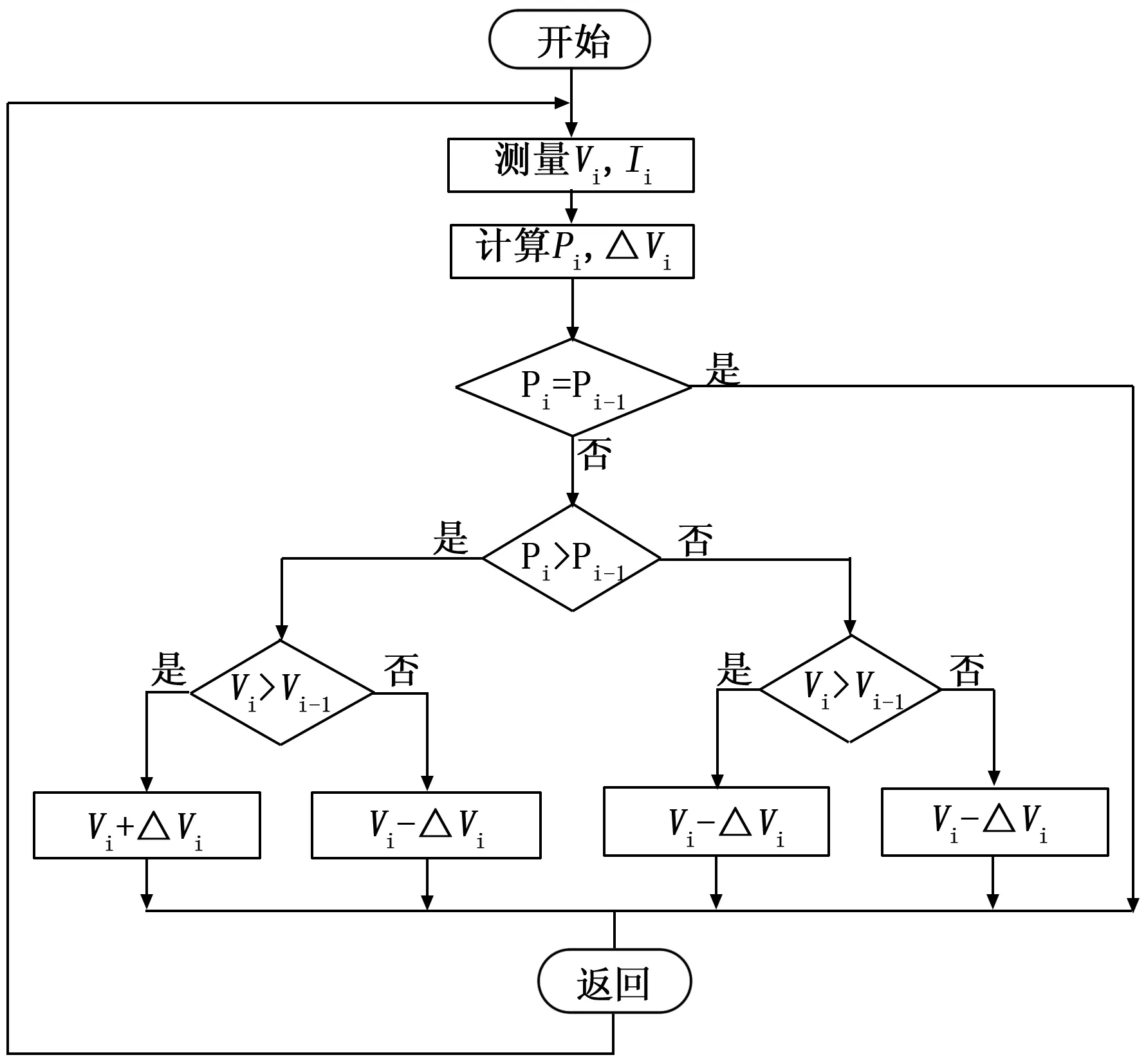
图4 自适应扰动观察算法流程图

规格参数光伏电池板光伏并网系统(10×2)最大功率Pmax (W)501000Pmax时的电压VMPP (V)17.4174Pmax时的电流IMPP (A)2.8755.75开路电压Voc (V)21.42214.2短路电流Isc (A)3.116.22

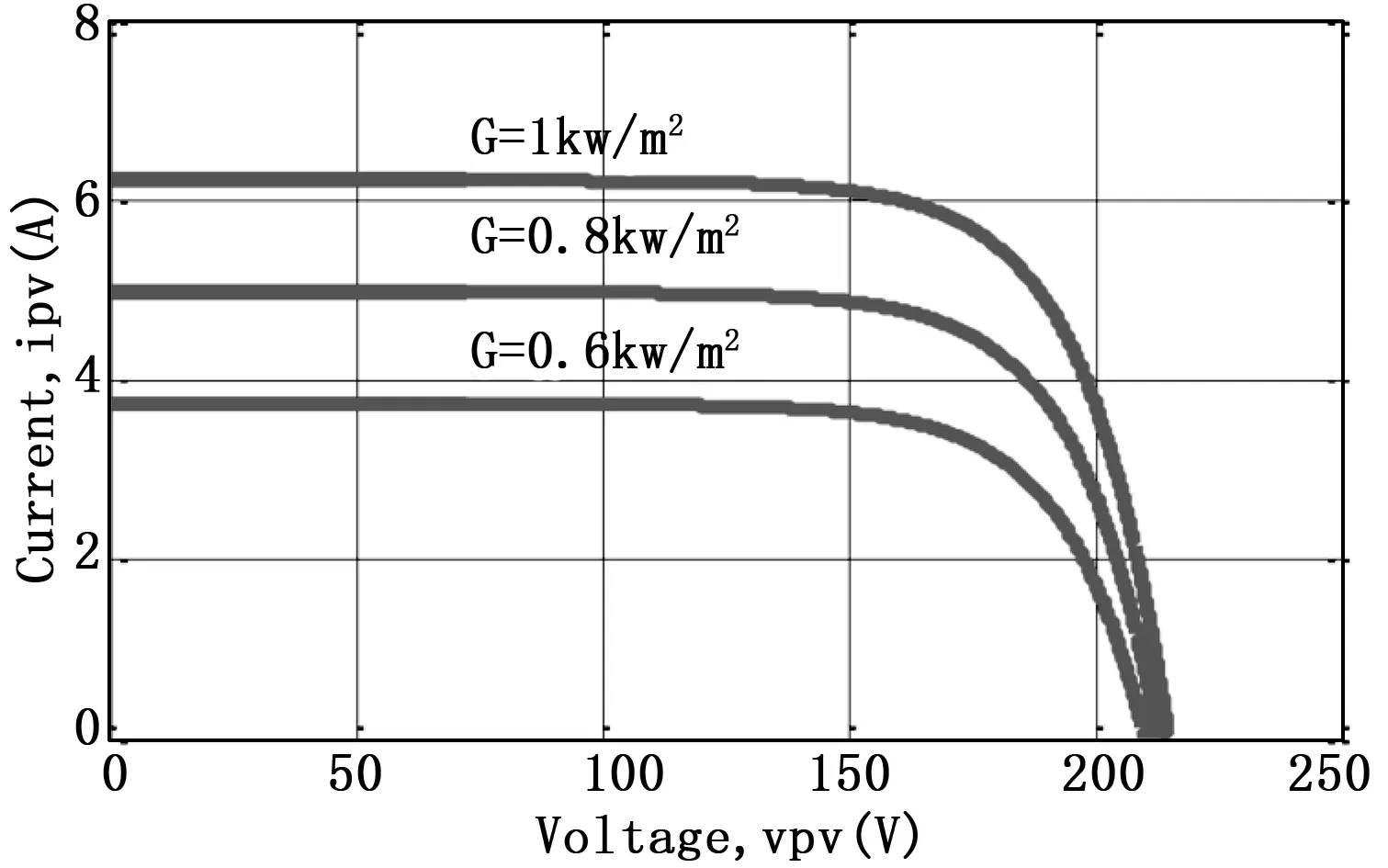
图5 不同太阳照射量时太阳能光伏系统的V-I特性，温度t=25℃

图5和图6分别是太阳能光伏系统，在不同的太阳照射量时的V-I和V-P特性，G=1，0.8和0.6 kW/m2，在该温度T= 25℃下。图5表明太阳能光伏电池板的电流，在太阳照射量增加时增加。图6表明了在不同的太阳照射量时的MPP点也不同。MPP点是PMPP1= 1000 W，G1= 1 kW/m2；PMPP2=789 W，G2=0.8 kW/m2和PMPP3=581 W，G3=0.6 kW/m2。因此提出了自适应扰动观察算法，来确定这些在不同的太阳照射量时的MPP点。

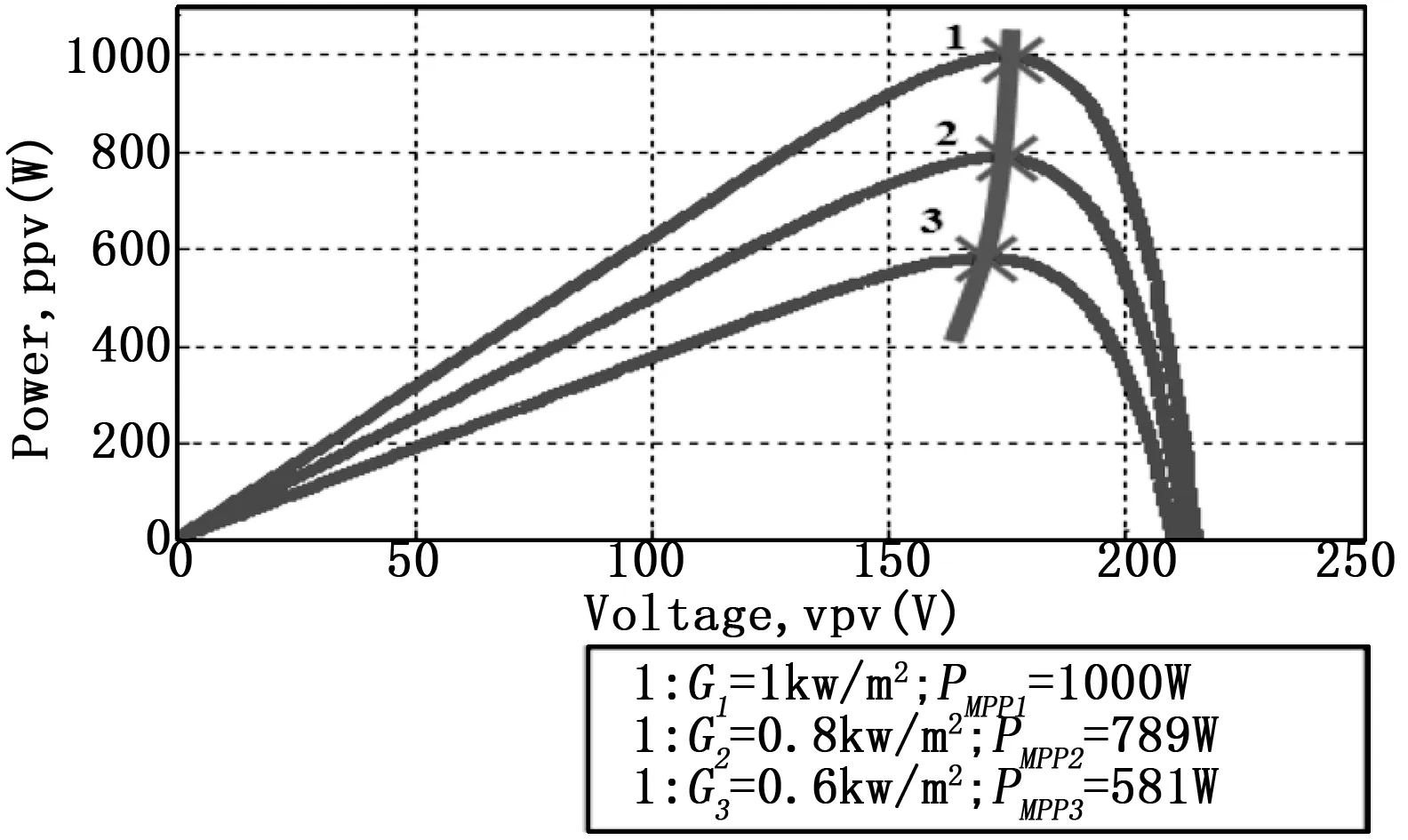
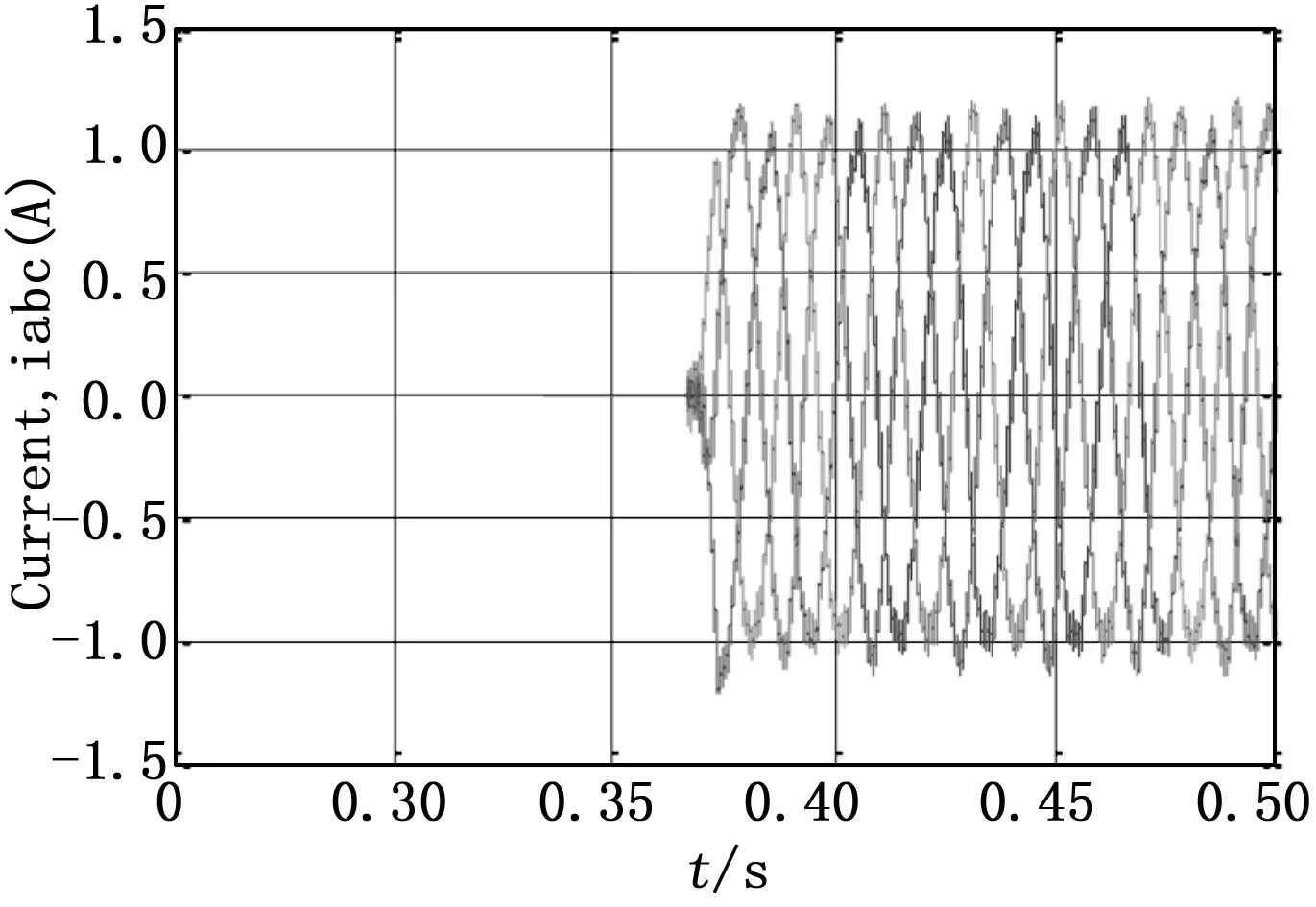
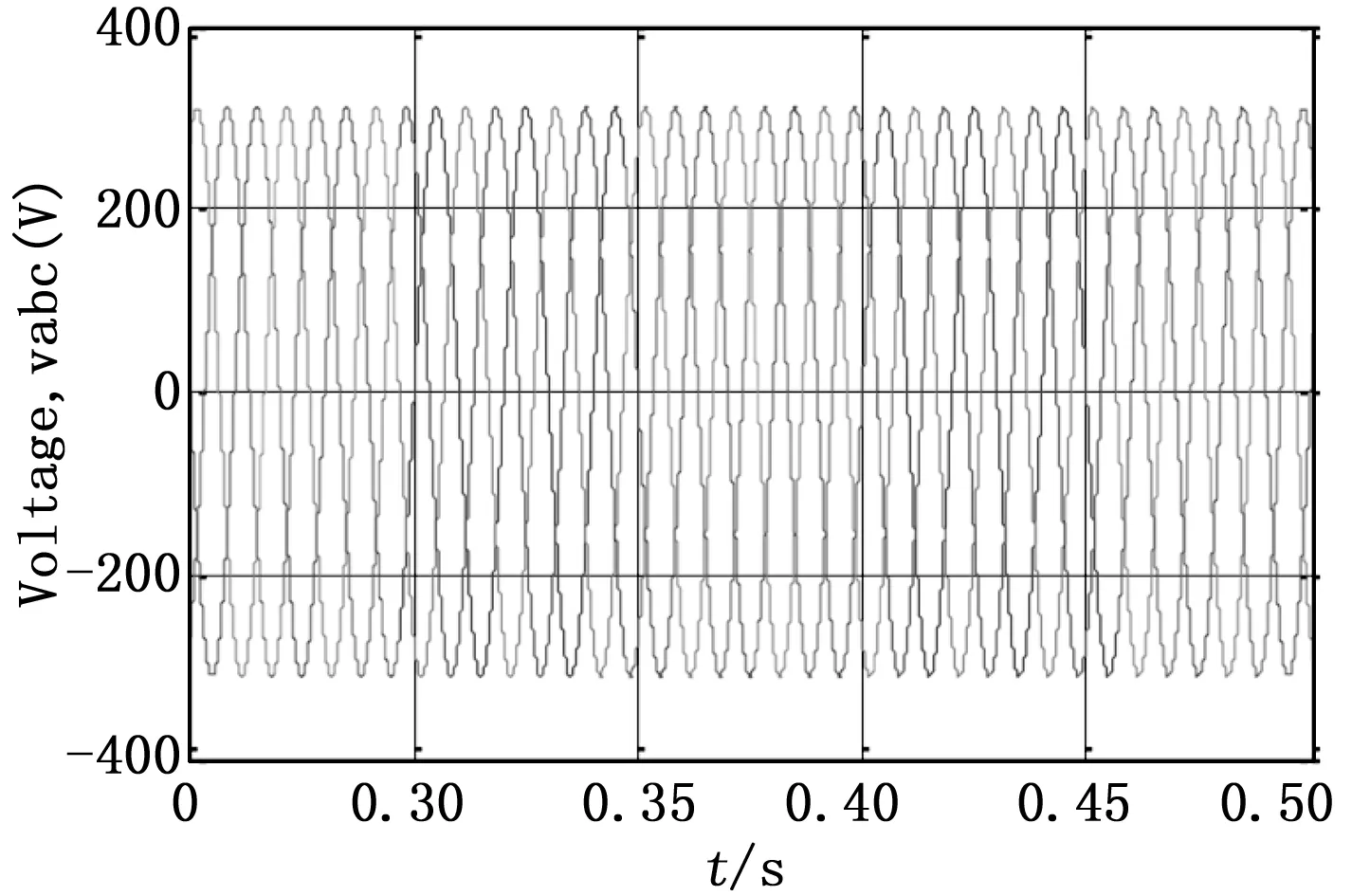
图6 不同太阳照射量时太阳能光伏系统的V-P特性，温度t=25℃

图7 采用传统的扰动观察算法，太阳能光伏并网系统在照射量g=1 kw/m2温度t=25℃的电流

图8 采用传统的扰动观察算法，太阳能光伏并网系统在照射量g=1 kw/m2温度t=25℃的电压

图7和图8分别是太阳能光伏并网系统，在太阳照射量G=1 kW/m2，温度T=25℃下，采用传统的扰动观察算法，太阳能光伏并网系统的电流和电压波形。太阳能光伏并网系统的电流在t=0.365 s达到稳定状态，如图7所示。然而，我们也发现太阳能光伏系统无法跟踪到MPP点，即PMPP=1 000 W，如图9所示，这意味着传统的扰动观察算法不收敛。

图9 采用传统的扰动观察算法，太阳能光伏并网系统的在照射量g=1 kw/m2温度t=25℃的功率

图10和11分别是太阳能光伏并网系统，在太阳照射量G=1 kW/m2，温度T=25℃下，采用自适应扰动观察算法，太阳能光伏并网系统的电流和电压波形。太阳能光伏并网系统的电流在t=0.273 s达到稳定状态，如图10所示。然而，我们也发现太阳能光伏系统跟踪到了MPP点，即PMPP=1000 W，如图12所示，这意味着采用自适应扰动观察算法，收敛值和速度都得到了改善。

通过自适应扰动观察算法与传统的扰动观察算法获得的功率对比，在太阳照射量G=1 kW/m2，温度T=25℃下，如图13所示，该对比确认了所提出的扰动观察算法的有效性。

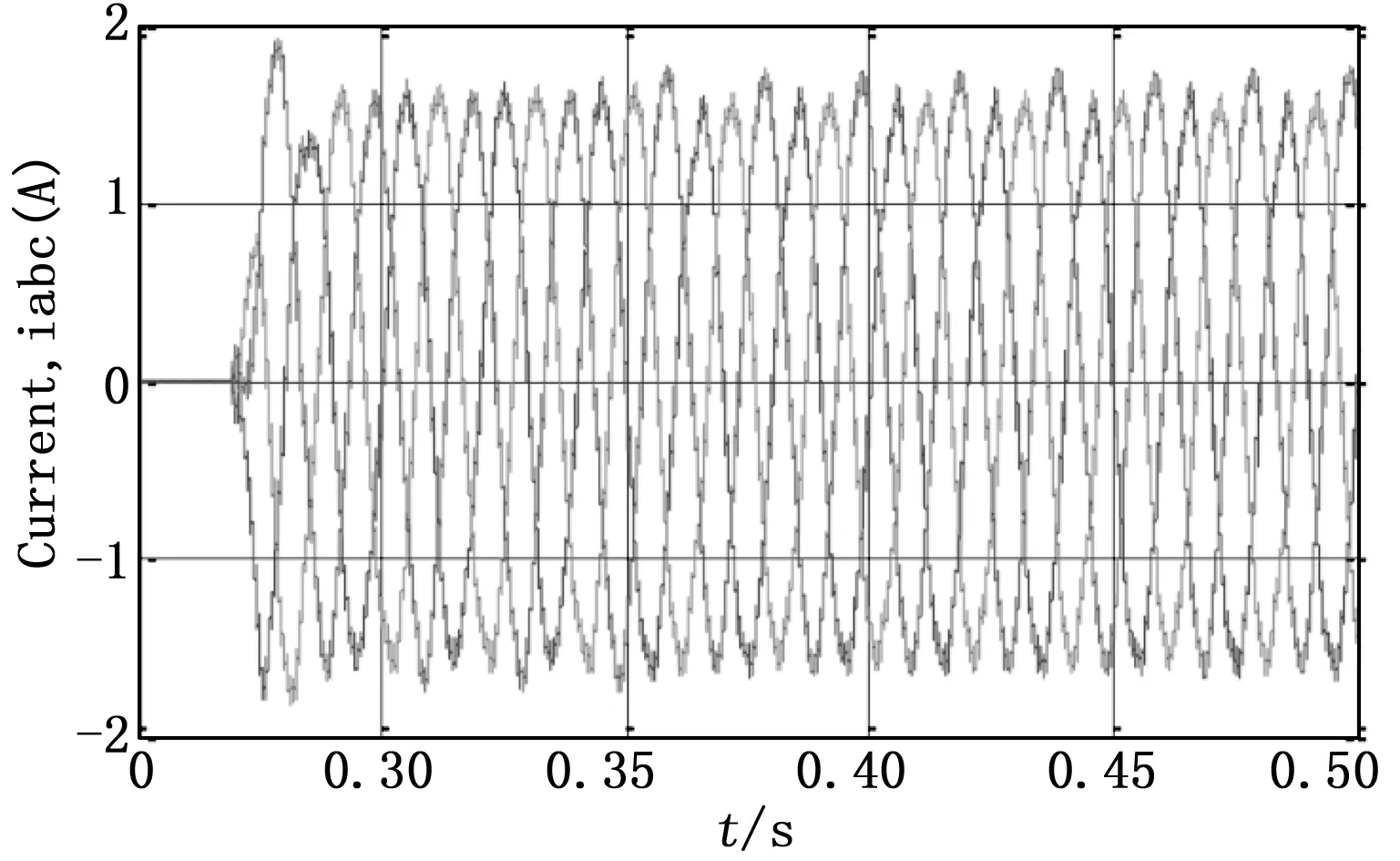
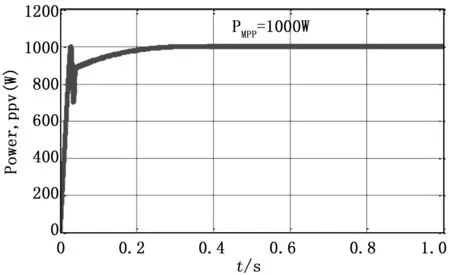
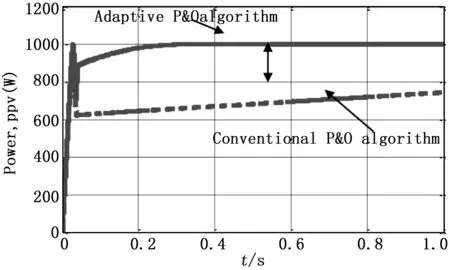
图10 采用自适应扰动观察算法，太阳能光伏并网系统在照射量g=1 kw/m2温度t=25℃的电流

图11 采用自适应扰动观察算法，太阳能光伏并网系统在照射量g=1 kw/m2温度t=25℃的电压

图12 采用自适应扰动观察算法，太阳能光伏并网系统的在照射量g=1 kw/m2温度t=25℃的功率

图13 自适应与传统扰动观察算法获得的功率对比，太阳能光伏并网系统的在照射量g=1 kw/m2温度t=25℃

从以上的一组波形对比中可以分析出，传统扰动观察算法当温度不变，仅太阳照射量从0 kW/m2升为1 kW/m2时，不能够快速地移动至最大功率点附近，而且输出的电压、功率波形振荡现象较严重。而新型的自适应扰动观察算法相比于传统的算法，能够更快速地移动到最大功率点，接近稳态时工作点会在最大功率点附近微小幅振荡，因而动态响应效果良好，稳态输出时电压、功率波形也比较平稳。

我们知道，相比于太阳照射量的影响，温度对太阳能光伏阵列各参数的影响并不大。因此，如果当光伏组件工作环境的温度突然变化时，所提出的该自适应的新方法在提高功率追踪速度、降低功率扰动的基础上能够保证跟踪的准确性。

两种MPPT算法的仿真结果对比显示，传统的扰动观察算法无法收敛，而收敛值和速度都通过采用自适应扰动观察算法得到了改善，稳定时间缩短25%，稳态值提高20%以上。

5 结论

本文利用自适应扰动观察(P&O)算法，提出了太阳能光伏并网系统的最大功率点跟踪(MPPT)控制策略。该方案使用了可变的扰动步长，该步长取决于各种大气条件。将得到的仿真结果与传统的P&O算法进行了比较，结果证明了所提出的MPPT控制策略对太阳能光伏并网系统的有效性。